- Research Article
- Open access
- Published:
Solvability of the Dirichlet Problem for Elliptic Equations in Weighted Sobolev Spaces on Unbounded Domains
Boundary Value Problems volume 2008, Article number: 901503 (2008)
Abstract
This paper is concerned with the study of the Dirichlet problem for a class of second-order linear elliptic equations in weighted Sobolev spaces on unbounded domains of  ,
,  . We state a regularity result and we can deduce an existence and uniqueness theorem.
. We state a regularity result and we can deduce an existence and uniqueness theorem.
1. Introduction
Consider the Dirichlet problem

where  is a sufficiently regular open subset of
is a sufficiently regular open subset of  ,
,  ,
,  is the uniformly elliptic second-order linear differential operator defined by
is the uniformly elliptic second-order linear differential operator defined by

with coefficients  .
.
It is well known that if  is bounded, the above problem has been largely studied by several authors under various hypotheses of discontinuity on the leading coefficients and considering the case
is bounded, the above problem has been largely studied by several authors under various hypotheses of discontinuity on the leading coefficients and considering the case  . In particular, some
. In particular, some  -bounds for the solutions of the problem (1.1) and related existence and uniqueness theorems have been obtained. Among the other results on this subject, we quote here the classical result of [1], where the author assumed that the
-bounds for the solutions of the problem (1.1) and related existence and uniqueness theorems have been obtained. Among the other results on this subject, we quote here the classical result of [1], where the author assumed that the  's belong to
's belong to  . This result was later generalized in different ways, supposing that the derivatives of the leading coefficients belong to some wider spaces. More recently, a relevant contribution to the theory has been given in [2–5], where the coefficients
. This result was later generalized in different ways, supposing that the derivatives of the leading coefficients belong to some wider spaces. More recently, a relevant contribution to the theory has been given in [2–5], where the coefficients  are assumed to be in the class VMO and
are assumed to be in the class VMO and  ; observe here that VMO contains the class
; observe here that VMO contains the class  .
.
If the set  is unbounded, under assumptions similar to those required in [1], problem (1.1) has for instance been studied in [6] with
is unbounded, under assumptions similar to those required in [1], problem (1.1) has for instance been studied in [6] with  , and in [7] with
, and in [7] with  . Instead, in [8, 9], the leading coefficients satisfy restrictions similar to those in [2, 3].
. Instead, in [8, 9], the leading coefficients satisfy restrictions similar to those in [2, 3].
In [10], we extended some results of [8, 9] to a weighted case. More precisely, we denoted by  a weight function belonging to a suitable class and such that
a weight function belonging to a suitable class and such that

Then we considered the problem

where  and
and  are some weighted Sobolev spaces and the weight functions are a suitable power of
are some weighted Sobolev spaces and the weight functions are a suitable power of  . We obtained that the operator
. We obtained that the operator  has closed range and that for the problem (1.4) a uniqueness result holds.
has closed range and that for the problem (1.4) a uniqueness result holds.
In this paper, we study again the problem (1.4). We state a regularity result which allows us to obtain the solvability of the problem.
A similar weighted case was studied in [11] with the leading coefficients satisfying hypotheses of Miranda's type and when  .
.
2. Weight Functions and Weighted Spaces
Let  be any Lebesgue measurable subset of
be any Lebesgue measurable subset of  and let
and let  be the collection of all Lebesgue measurable subsets of
be the collection of all Lebesgue measurable subsets of  . Let
. Let  . Denote by
. Denote by  the Lebesgue measure of
the Lebesgue measure of  , by
, by  the characteristic function of
the characteristic function of  and by
and by  the class of restrictions to
the class of restrictions to  of functions
of functions  with
with  . Moreover, if
. Moreover, if  is a space of functions defined on
is a space of functions defined on  , we denote by
, we denote by  the class of all functions
the class of all functions  such that
such that  for any
for any 
 . Finally, for any
. Finally, for any  and
and  , we put
, we put  ,
,  and
and 
Let  be an open subset of
be an open subset of  . We introduce a class of weight functions defined on
. We introduce a class of weight functions defined on  . Denote by
. Denote by  the set of all measurable functions
the set of all measurable functions  such that
such that

where  is independent of
is independent of  and
and  .
.
We note that the class of all functions  which are Lipschitz continuous in
which are Lipschitz continuous in  with Lipschitz coefficient
with Lipschitz coefficient  is contained in
is contained in  (see [12]).
(see [12]).
For  , we put
, we put

It is known that

We assign an unbounded open subset  of
of  .
.
From now on, let  be a function such that
be a function such that  and
and

For example,

We put

and note that  .
.
For any  and
and  , we set
, we set

and note that

where  depend only on
depend only on  (see [12]).
(see [12]).
If  is a real function defined in
is a real function defined in  , we denote by
, we denote by  the zero extension of
the zero extension of  in
in  .
.
We begin to prove the following.
Lemma 2.1.
If  are two nonnegative functions in
are two nonnegative functions in  , respectively, then for any
, respectively, then for any 

and for  the following also hold:
the following also hold:

Proof.
The equality (2.9) follows by

Prove now the inequality (2.10). We observe that:

where we have put

On the other hand,

Therefore, from (2.12) and (2.14), we deduce that

By (2.15), it obviously follows

and (2.16) yields the inequality (2.10).
If  ,
,  and
and  , consider the space
, consider the space  of distributions
of distributions  on
on  such that
such that  for
for  , equipped with the norm
, equipped with the norm

Moreover, denote by  the closure of
the closure of  in
in  and put
and put  . A more detailed account of properties of the above-defined spaces can be found, for instance, in [14].
. A more detailed account of properties of the above-defined spaces can be found, for instance, in [14].
From Lemma 2.1 we can deduce another lemma which we will need in the proof of our regularity result.
Lemma 2.2.
Let  and
and  . Then
. Then  if and only if
if and only if  and the function
and the function  belongs to
belongs to  . In addition, there exist
. In addition, there exist  such that
such that

where  and
and  depend only on
depend only on  and
and  . Moreover, if
. Moreover, if  and
and  , then the function
, then the function  belongs to
belongs to  and the following estimate holds:
and the following estimate holds:

with  dependent only on
dependent only on  and
and  .
.
Proof.
The first part of the lemma follows from (2.9) for  and
and  , if one uses (2.1) and (2.8). The second part of the lemma follows in a similar way from the inequality (2.10), if one puts
, if one uses (2.1) and (2.8). The second part of the lemma follows in a similar way from the inequality (2.10), if one puts  ,
,  , and
, and  .
.
3. An Embedding Lemma
We now recall the definitions of the function spaces in which the coefficients of the operator will be chosen. If  has the property
has the property

where  is a positive constant independent of
is a positive constant independent of  and
and  , it is possible to consider the space
, it is possible to consider the space  (
( ) of functions
) of functions  such that
such that

where

If  , where
, where

we will say that  if
if  for
for  . A function
. A function

is called a modulus of continuity of  in
in  if
if

For  and
and  , we denote by
, we denote by  the set of all functions
the set of all functions  in
in  such that
such that

endowed with the norm defined by (3.7). Then we define  as the closure of
as the closure of  in
in  and
and  as the closure of
as the closure of  in
in  . In particular, we put
. In particular, we put  ,
,  and
and  . In order to define the modulus of continuity of a function
. In order to define the modulus of continuity of a function  in
in  , recall first that for a function
, recall first that for a function  the following characterization holds:
the following characterization holds:

where

Thus the modulus of continuity of  is a function
is a function

such that

A more detailed account of properties of the above defined function spaces can be found in [6, 15, 16].
We consider the following condition:
(h0) has the cone property,
has the cone property,  are numbers such that
are numbers such that

From [17, Theorem 3.1] we have the following.
Lemma 3.1.
If the assumption (h0) holds, then for any  , it results that??
, it results that?? and
and

with  dependent only on
dependent only on  and
and 
4. A Regularity Result
Assume that  is an unbounded open subset of
is an unbounded open subset of  , with the uniform
, with the uniform  -regularity property, and let
-regularity property, and let  be the function defined by (2.6). Moreover, let
be the function defined by (2.6). Moreover, let  and
and  . Consider in
. Consider in  the differential operator
the differential operator

with the following conditions on the coefficients:
(h1)

there exist functions  ,
,  ,
,  and
and  such that
such that
(h2)

(h3)

where

Observe that under the assumptions (h1)–(h3), it follows that the operator  is bounded from Lemma 3.1.
is bounded from Lemma 3.1.
Theorem 4.1.
Suppose that the assumptions (h1), (h2), and (h3) hold, and let  be a solution of the problem
be a solution of the problem

where  and
and  . Then
. Then  belongs to
belongs to  .
.
Proof.
By [8, Lemma 4.1], we have

We choose  , with
, with  and a function
and a function  such that
such that

where  depends only on
depends only on  .
.
We fix  and put
and put

Clearly, we have

Since  , from [8, Theorem 3.1] it follows that
, from [8, Theorem 3.1] it follows that

with  depending on
depending on  ,
,  ,
,  ,
,  , where
, where  depends on
depends on  and
and  is a function in
is a function in  such that
such that

Since

from (4.11) and (4.13), we have

with  depending on the same parameters of
depending on the same parameters of  .
.
From Lemma 3.1 with  , we have that
, we have that

with  dependent on
dependent on  and
and  .
.
Using [18, Corollary 4.5], we can obtain the following interpolation estimates:

where  depends on
depends on  and the constants
and the constants  and
and  depend on
depend on  .
.
Thus by (4.14)–(4.16), with easy computations, we deduce the following bound:

where  depends on
depends on  ,
,  ,
,  ,
,  ,
,  .
.
By a well-known lemma of monotonicity of Miranda (see [19, Lemma 3.1]), it follows from (4.17) that

and then, using Young's inequality, we deduce from (4.18) that

with  dependent on the same parameters of
dependent on the same parameters of  .
.
From (4.19) it follows that

where  depends on the same parameters of
depends on the same parameters of  .
.
By (4.20) and by Lemma 2.2, we have that

with  dependent on the same parameters of
dependent on the same parameters of  and on
and on  .
.
Therefore, from (4.21), we have the result.
5. Existence and Uniqueness Results
In this section, we will prove our existence and uniqueness theorem. To this aim, we need two preliminary lemmas.
Observe that it is possible to find a function  which is equivalent to
which is equivalent to  and such that
and such that

where  is independent of
is independent of  (see [12]).
(see [12]).
Lemma 5.1.
The Dirichlet problem

where

is uniquely solvable. Moreover, if  , then the solution
, then the solution  belongs to
belongs to  for all
for all  in
in  .
.
Proof.
Note that  is a solution of problem (5.2) if and only if
is a solution of problem (5.2) if and only if  is a solution of the problem
is a solution of the problem

But for any 

then (5.4) is equivalent to the problem

where we have put

Using [7, Theorem 5.2], [6, Equation (1.6)], and (5.1), we obtain that (5.6) is uniquely solvable and then problem (5.2) is uniquely solvable too.
Moreover, if  , then also
, then also  . Therefore, using the theorem in [20], we have that the solution
. Therefore, using the theorem in [20], we have that the solution  of (5.6) belongs to
of (5.6) belongs to  for all
for all  , and so the solution
, and so the solution  of (5.2) lies in
of (5.2) lies in  for all
for all  .
.
Lemma 5.2.
The Dirichlet problem

is uniquely solvable, where  is defined by (5.3).
is defined by (5.3).
Proof.
Let  be a function in
be a function in  . Then, by Lemma 5.1, there exists a unique
. Then, by Lemma 5.1, there exists a unique  (for all
(for all  ) such that
) such that  .
.
Firstly, suppose that  . It follows from Theorem 4.1 that
. It follows from Theorem 4.1 that  belongs to
belongs to  . Moreover, by [10, Lemma 2.2],
. Moreover, by [10, Lemma 2.2],  lies in
lies in  .
.
Suppose now  . Then
. Then  (for all
(for all  ) and then, using again Theorem 4.1,
) and then, using again Theorem 4.1,  belongs to
belongs to  . Moreover, by [10, Lemma 2.2],
. Moreover, by [10, Lemma 2.2],  lies in
lies in  .
.
Therefore, in both cases,  and it is a solution of the equation
and it is a solution of the equation  , so that
, so that  . Since
. Since  is dense in
is dense in  (see [14, Proposition 1.1]) and
(see [14, Proposition 1.1]) and  is a closed subspace of
is a closed subspace of  by [10, Theorem 4.1], we obtain that
by [10, Theorem 4.1], we obtain that  . The uniqueness of the solution follows from [10, Theorem 5.2].
. The uniqueness of the solution follows from [10, Theorem 5.2].
Finally, adding the following assumption on the coefficients of  :
:
(h4)

we are now in position to state the following uniqueness and existence result.
Theorem 5.3.
Suppose that conditions (h1)–(h4) hold. In addition, assume that  a.e. in
a.e. in  . Then the problem
. Then the problem

is uniquely solvable.
Proof.
For each  put
put

The function

is clearly continuous; moreover, it is easy to show that the coefficients of each operator  satisfy the hypotheses of [10, Theorem 5.2] (see also [16, Lemma 3.2]), and hence
satisfy the hypotheses of [10, Theorem 5.2] (see also [16, Lemma 3.2]), and hence  . On the other hand, it follows from [10, Theorem 4.1] that
. On the other hand, it follows from [10, Theorem 4.1] that  is closed for any
is closed for any  , so that [9, Lemma 4.1] can be used to obtain the existence of
, so that [9, Lemma 4.1] can be used to obtain the existence of  such that
such that

By Lemma 5.2, the problem

is uniquely solvable.
Therefore, this latter result and estimate (5.13) allow to use the method of continuity along a parameter in order to prove that the problem

is likewise uniquely solvable. The proof is complete.
References
Miranda C: Sulle equazioni ellittiche del secondo ordine di tipo non variazionale, a coefficienti discontinui. Annali di Matematica Pura ed Applicata 1963,63(1):353-386. 10.1007/BF02412185
Chiarenza F, Frasca M, Longo P:Interior
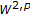 estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149-168.
estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149-168.Chiarenza F, Frasca M, Longo P:
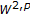 -solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841-853. 10.2307/2154379
-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841-853. 10.2307/2154379Vitanza C:
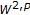 -regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1992,47(1):177-186.
-regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1992,47(1):177-186.Vitanza C:A new contribution to the
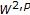 regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1993,48(2):287-296.
regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1993,48(2):287-296.Transirico M, Troisi M: Equazioni ellittiche del secondo ordine di tipo non variazionale in aperti non limitati. Annali di Matematica Pura ed Applicata 1988,152(1):209-226. 10.1007/BF01766150
Caso L, Cavaliere P, Transirico M:Solvability of the Dirichlet problem in
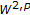 for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche 2002,57(2):287-302.
for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche 2002,57(2):287-302.Caso L, Cavaliere P, Transirico M: Uniqueness results for elliptic equations VMO-coefficients. International Journal of Pure and Applied Mathematics 2004,13(4):499-512.
Caso L, Cavaliere P, Transirico M: An existence result for elliptic equations with VMO-coefficients. Journal of Mathematical Analysis and Applications 2007,325(2):1095-1102. 10.1016/j.jmaa.2006.02.048
Boccia S, Monsurrò S, Transirico M: Elliptic equations in weighted Sobolev spaces on unbounded domains. International Journal of Mathematics and Mathematical Sciences to appear
Di Gironimo P, Transirico M: Second order elliptic equations in weighted Sobolev spaces on unbounded domains. Rendiconti della Accademia Nazionale delle Scienze detta dei XL. Serie V. Memorie di Matematica 1991, 15: 163-176.
Troisi M: Su una classe di funzioni peso. Rendiconti della Accademia Nazionale delle Scienze detta dei XL. Serie V. Memorie di Matematica 1986,10(1):141-152.
Caso L, Transirico M: Some remarks on a class of weight functions. Commentationes Mathematicae Universitatis Carolinae 1996,37(3):469-477.
Troisi M: Su una classe di spazi di Sobolev con peso. Rendiconti della Accademia Nazionale delle Scienze detta dei XL. Serie V. Memorie di Matematica 1986,10(1):177-189.
Transirico M, Troisi M, Vitolo A: Spaces of Morrey type and elliptic equations in divergence form on unbounded domains. Bollettino dell'Unione Matematica Italiana. Serie VIII. B 1995,9(1):153-174.
Transirico M, Troisi M, Vitolo A:
 spaces on domains of
spaces on domains of  Ricerche di Matematica 1996,45(2):355-378.
Ricerche di Matematica 1996,45(2):355-378.Glushak AV, Transirico M, Troisi M: Teoremi di immersione ed equazioni ellittiche in aperti non limitati. Rendiconti di Matematica e delle sue Applicazioni 1989,9(1):113-130.
Boccia S, Caso L: Interpolation inequalities in weighted Sobolev spaces. Journal of Mathematical Inequalities to appear
Miranda C: Teoremi di unicità in domini non limitati e teoremi di Liouville per le soluzioni dei problemi al contorno relativi alle equazioni ellittiche. Annali di Matematica Pura ed Applicata 1962,59(1):189-212. 10.1007/BF02411730
Lions P-L: Remarques sur les équations linéaires elliptiques du second ordre sous forme divergence dans les domaines non bornés. Atti della Accademia Nazionale dei Lincei. Rendiconti. Classe di Scienze Fisiche, Matematiche e Naturali 1985,78(5):205-212.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boccia, S., Monsurrò, S. & Transirico, M. Solvability of the Dirichlet Problem for Elliptic Equations in Weighted Sobolev Spaces on Unbounded Domains. Bound Value Probl 2008, 901503 (2008). https://doi.org/10.1155/2008/901503
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/901503
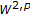 estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149-168.
estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche di Matematica 1991,40(1):149-168.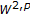 -solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841-853. 10.2307/2154379
-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients. Transactions of the American Mathematical Society 1993,336(2):841-853. 10.2307/2154379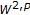 -regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1992,47(1):177-186.
-regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1992,47(1):177-186. regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1993,48(2):287-296.
regularity for a class of elliptic second order equations with discontinuous coefficients. Le Matematiche 1993,48(2):287-296. for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche 2002,57(2):287-302.
for elliptic equations with discontinuous coefficients in unbounded domains. Le Matematiche 2002,57(2):287-302. spaces on domains of
spaces on domains of  Ricerche di Matematica 1996,45(2):355-378.
Ricerche di Matematica 1996,45(2):355-378.