- Research Article
- Open access
- Published:
Existence of Pseudo Almost Automorphic Solutions for the Heat Equation with 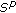 -Pseudo Almost Automorphic Coefficients
-Pseudo Almost Automorphic Coefficients
Boundary Value Problems volume 2009, Article number: 182527 (2009)
Abstract
We obtain the existence of pseudo almost automorphic solutions to the  -dimensional heat equation with
-dimensional heat equation with  -pseudo almost automorphic coefficients.
-pseudo almost automorphic coefficients.
1. Introduction
Let  be an open bounded subset with
be an open bounded subset with  boundary
boundary  , and let
, and let  be the space square integrable functions equipped with its natural
be the space square integrable functions equipped with its natural  topology. Of concern is the study of pseudo almost automorphic solutions to the
topology. Of concern is the study of pseudo almost automorphic solutions to the  -dimensional heat equation with divergence terms
-dimensional heat equation with divergence terms

where the symbols  and
and  stand, respectively, for the first- and second-order differential operators defined by
stand, respectively, for the first- and second-order differential operators defined by

and the coefficients  are
are  -pseudo almost automorphic.
-pseudo almost automorphic.
To analyze (1.1), our strategy will consist of studying the existence of pseudo almost automorphic solutions to the class of partial hyperbolic differential equations

where  is a sectorial linear operator on a Banach space
is a sectorial linear operator on a Banach space  whose corresponding analytic semigroup
whose corresponding analytic semigroup  is hyperbolic; that is,
is hyperbolic; that is,  the operator
the operator  are arbitrary linear (possibly unbounded) operators on
are arbitrary linear (possibly unbounded) operators on  , and
, and  are
are  -pseudo almost automorphic for
-pseudo almost automorphic for  and jointly continuous functions.
and jointly continuous functions.
Indeed, letting  for all
for all  ,
,  for all
for all  and
and  and
and  , one can readily see that (1.1) is a particular case of (1.3).
, one can readily see that (1.1) is a particular case of (1.3).
The concept of pseudo almost automorphy, which is the central tool here, was recently introduced in literature by Liang et al. [1, 2]. The pseudo almost automorphy is a generalization of both the classical almost automorphy due to Bochner [3] and that of pseudo almost periodicity due to Zhang [4–6]. It has recently generated several developments and extensions. For the most recent developments, we refer the reader to [1, 2, 7–9]. More recently, in Diagana [7], the concept of  -pseudo almost automorphy (or Stepanov-like pseudo almost automorphy) was introduced. It should be mentioned that the
-pseudo almost automorphy (or Stepanov-like pseudo almost automorphy) was introduced. It should be mentioned that the  -pseudo almost automorphy is a natural generalization of the notion of pseudo almost automorphy.
-pseudo almost automorphy is a natural generalization of the notion of pseudo almost automorphy.
In this paper, we will make extensive use of the concept of  -pseudo almost automorphy combined with the techniques of hyperbolic semigroups to study the existence of pseudo almost automorphic solutions to the class of partial hyperbolic differential equations appearing in (1.3) and then to the
-pseudo almost automorphy combined with the techniques of hyperbolic semigroups to study the existence of pseudo almost automorphic solutions to the class of partial hyperbolic differential equations appearing in (1.3) and then to the  -dimensional heat equation (1.1).
-dimensional heat equation (1.1).
In this paper, as in the recent papers [10–12], we consider a general intermediate space  between
between  and
and  . In contrast with the fractional power spaces considered in some recent papers by Diagana [13], the interpolation and Hölder spaces, for instance, depend only on
. In contrast with the fractional power spaces considered in some recent papers by Diagana [13], the interpolation and Hölder spaces, for instance, depend only on  and
and  and can be explicitly expressed in many concrete cases. Literature related to those intermediate spaces is very extensive; in particular, we refer the reader to the excellent book by Lunardi [14], which contains a comprehensive presentation on this topic and related issues.
and can be explicitly expressed in many concrete cases. Literature related to those intermediate spaces is very extensive; in particular, we refer the reader to the excellent book by Lunardi [14], which contains a comprehensive presentation on this topic and related issues.
Existence results related to pseudo almost periodic and almost automorphic solutions to the partial hyperbolic differential equations of the form (1.3) have recently been established in [12, 15–18], respectively. Though to the best of our knowledge, the existence of pseudo almost automorphic solutions to the heat equation (1.1) in the case when the coefficients  are
are  -pseudo almost automorphic is an untreated original problem and constitutes the main motivation of the present paper.
-pseudo almost automorphic is an untreated original problem and constitutes the main motivation of the present paper.
2. Preliminaries
Let  be two Banach spaces. Let
be two Banach spaces. Let  (resp.,
(resp.,  ) denote the collection of all
) denote the collection of all  -valued bounded continuous functions (resp., the class of jointly bounded continuous functions
-valued bounded continuous functions (resp., the class of jointly bounded continuous functions  ). The space
). The space  equipped with the sup norm
equipped with the sup norm  is a Banach space. Furthermore,
is a Banach space. Furthermore,  (resp.,
(resp.,  ) denotes the class of continuous functions from
) denotes the class of continuous functions from  into
into  (resp., the class of jointly continuous functions
(resp., the class of jointly continuous functions  ).
).
The notation  stands for the Banach space of bounded linear operators from
stands for the Banach space of bounded linear operators from  into
into  equipped with its natural topology; in particular, this is simply denoted
equipped with its natural topology; in particular, this is simply denoted  whenever
whenever  .
.
Definition 2.1 (see [19]).
The Bochner transform  ,
,  ,
,  of a function
of a function  is defined by
is defined by 
Remark 2.2.
-
(i)
A function
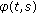 ,
, 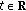 ,
,  , is the Bochner transform of a certain function
, is the Bochner transform of a certain function 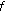 ,
, 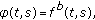 if and only if
if and only if 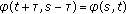 for all
for all  ,
, 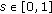 and
and  .
. -
(ii)
Note that if
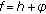 , then
, then 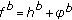 . Moreover,
. Moreover, 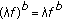 for each scalar
for each scalar  .
.
Definition 2.3.
The Bochner transform  ,
,  ,
,  ,
,  of a function
of a function  on
on  , with values in
, with values in  , is defined by
, is defined by  for each
for each  .
.
Definition 2.4.
Let  . The space
. The space  of all Stepanov bounded functions, with the exponent
of all Stepanov bounded functions, with the exponent  , consists of all measurable functions
, consists of all measurable functions  such that
such that  . This is a Banach space with the norm
. This is a Banach space with the norm

2.1. 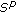 -Pseudo Almost Periodicity
-Pseudo Almost Periodicity
Definition 2.5.
A function  is called (Bohr) almost periodic if for each
is called (Bohr) almost periodic if for each  there exists
there exists  such that every interval of length
such that every interval of length  contains a number
contains a number  with the property that
with the property that

The number  above is called an
above is called an  -translation number of
-translation number of  , and the collection of all such functions will be denoted
, and the collection of all such functions will be denoted  .
.
Definition 2.6.
A function  is called (Bohr) almost periodic in
is called (Bohr) almost periodic in  uniformly in
uniformly in  where
where  is any compact subset
is any compact subset  if for each
if for each  there exists
there exists  such that every interval of length
such that every interval of length  contains a number
contains a number  with the property that
with the property that

The collection of those functions is denoted by  .
.
Define the classes of functions  and
and  , respectively, as follows:
, respectively, as follows:

and  is the collection of all functions
is the collection of all functions  such that
such that

uniformly in  .
.
Definition 2.7 (see [13]).
A function  is called pseudo almost periodic if it can be expressed as
is called pseudo almost periodic if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
Definition 2.8 (see [13]).
A function  is said to be pseudo almost periodic if it can be expressed as
is said to be pseudo almost periodic if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
Define  as the collection of all functions
as the collection of all functions  such that
such that

uniformly in  , where
, where  is any bounded subset.
is any bounded subset.
Obviously,

A weaker version of Definition 2.8 is the following.
Definition 2.9.
A function  is said to be B-pseudo almost periodic if it can be expressed as
is said to be B-pseudo almost periodic if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
Definition 2.10 (see [20, 21]).
A function  is called
is called  -pseudo almost periodic (or Stepanov-like pseudo almost periodic) if it can be expressed as
-pseudo almost periodic (or Stepanov-like pseudo almost periodic) if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
In other words, a function  is said to be
is said to be  -pseudo almost periodic if its Bochner transform
-pseudo almost periodic if its Bochner transform  is pseudo almost periodic in the sense that there exist two functions
is pseudo almost periodic in the sense that there exist two functions  such that
such that  , where
, where  and
and  .
.
To define the notion of  -pseudo almost automorphy for functions of the form
-pseudo almost automorphy for functions of the form  , we need to define the
, we need to define the  -pseudo almost periodicity for these functions as follows.
-pseudo almost periodicity for these functions as follows.
Definition 2.11.
A function  with
with  for each
for each  , is said to be
, is said to be  -pseudo almost periodic if there exist two functions
-pseudo almost periodic if there exist two functions  such that
such that  , where
, where  and
and  .
.
The collection of those  -pseudo almost periodic functions
-pseudo almost periodic functions  will be denoted
will be denoted  .
.
2.2. 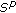 -Almost Automorphy
-Almost Automorphy
The notion of  -almost automorphy is a new notion due to N'Guérékata and Pankov [22].
-almost automorphy is a new notion due to N'Guérékata and Pankov [22].
Definition 2.12 (Bochner).
A function  is said to be almost automorphic if for every sequence of real numbers
is said to be almost automorphic if for every sequence of real numbers  there exists a subsequence
there exists a subsequence  such that
such that

is well defined for each  , and
, and

for each  .
.
Remark 2.13.
The function  in Definition 2.12 is measurable but not necessarily continuous. Moreover, if
in Definition 2.12 is measurable but not necessarily continuous. Moreover, if  is continuous, then
is continuous, then  is uniformly continuous. If the convergence above is uniform in
is uniformly continuous. If the convergence above is uniform in  , then
, then  is almost periodic. Denote by
is almost periodic. Denote by  the collection of all almost automorphic functions
the collection of all almost automorphic functions  . Note that
. Note that  equipped with the sup norm,
equipped with the sup norm,  , turns out to be a Banach space.
, turns out to be a Banach space.
We will denote by  the closed subspace of all functions
the closed subspace of all functions  with
with  . Equivalently,
. Equivalently,  if and only if
if and only if  is almost automorphic, and the convergences in Definition 2.12 are uniform on compact intervals, that is, in the Fréchet space
is almost automorphic, and the convergences in Definition 2.12 are uniform on compact intervals, that is, in the Fréchet space  . Indeed, if
. Indeed, if  is almost automorphic, then its range is relatively compact. Obviously, the following inclusions hold:
is almost automorphic, then its range is relatively compact. Obviously, the following inclusions hold:

Definition 2.14 (see [22]).
The space  of Stepanov-like almost automorphic functions (or
of Stepanov-like almost automorphic functions (or  -almost automorphic) consists of all
-almost automorphic) consists of all  such that
such that  . That is, a function
. That is, a function  is said to be
is said to be  -almost automorphic if its Bochner transform
-almost automorphic if its Bochner transform  is almost automorphic in the sense that for every sequence of real numbers
is almost automorphic in the sense that for every sequence of real numbers  there exists a subsequence
there exists a subsequence  and a function
and a function  such that
such that

as  pointwise on
pointwise on  .
.
Remark 2.15.
It is clear that if  and
and  is
is  -almost automorphic, then
-almost automorphic, then  is
is  -almost automorphic. Also if
-almost automorphic. Also if  , then
, then  is
is  -almost automorphic for any
-almost automorphic for any  . Moreover, it is clear that
. Moreover, it is clear that  if and only if
if and only if  . Thus,
. Thus,  can be considered as
can be considered as  .
.
Definition 2.16.
A function  with
with  for each
for each  , is said to be
, is said to be  -almost automorphic in
-almost automorphic in  uniformly in
uniformly in  if
if  is
is  -almost automorphic for each
-almost automorphic for each  ; that is, for every sequence of real numbers
; that is, for every sequence of real numbers  , there exists a subsequence
, there exists a subsequence  and a function
and a function  such that
such that

as  pointwise on
pointwise on  for each
for each  .
.
The collection of those  -almost automorphic functions
-almost automorphic functions  will be denoted by
will be denoted by  .
.
2.3. Pseudo Almost Automorphy
The notion of pseudo almost automorphy is a new notion due to Liang et al. [2, 9].
Definition 2.17.
A function  is called pseudo almost automorphic if it can be expressed as
is called pseudo almost automorphic if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
Obviously, the following inclusions hold:

Definition 2.18.
A function  is said to be pseudo almost automorphic if it can be expressed as
is said to be pseudo almost automorphic if it can be expressed as  where
where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
A substantial result is the next theorem, which is due to Liang et al. [2].
Theorem 2.19 (see [2]).
The space  equipped with the sup norm
equipped with the sup norm  is a Banach space.
is a Banach space.
We also have the following composition result.
Theorem 2.20 (see [2]).
If  belongs to
belongs to  and if
and if  is uniformly continuous on any bounded subset
is uniformly continuous on any bounded subset  of
of  for each
for each  , then the function defined by
, then the function defined by  belongs to
belongs to  provided
provided  .
.
3.  -Pseudo Almost Automorphy
-Pseudo Almost Automorphy
This section is devoted to the notion of  -pseudo almost automorphy. Such a concept is completely new and is due to Diagana [7].
-pseudo almost automorphy. Such a concept is completely new and is due to Diagana [7].
Definition 3.1 (see [7]).
A function  is called
is called  -pseudo almost automorphic (or Stepanov-like pseudo almost automorphic) if it can be expressed as
-pseudo almost automorphic (or Stepanov-like pseudo almost automorphic) if it can be expressed as

where  and
and  . The collection of such functions will be denoted by
. The collection of such functions will be denoted by  .
.
Clearly, a function  is said to be
is said to be  -pseudo almost automorphic if its Bochner transform
-pseudo almost automorphic if its Bochner transform  is pseudo almost automorphic in the sense that there exist two functions
is pseudo almost automorphic in the sense that there exist two functions  such that
such that  , where
, where  and
and 
Theorem 3.2 (see [7]).
If  , then
, then  for each
for each  . In other words,
. In other words,  .
.
Obviously, the following inclusions hold:

Theorem 3.3 (see [7]).
The space  equipped with the norm
equipped with the norm  is a Banach space.
is a Banach space.
Definition 3.4.
A function  with
with  for each
for each  , is said to be
, is said to be  -pseudo almost automorphic if there exists two functions
-pseudo almost automorphic if there exists two functions  such that
such that

where  and
and  . The collection of those
. The collection of those  -pseudo almost automorphic functions will be denoted by
-pseudo almost automorphic functions will be denoted by  .
.
We have the following composition theorems.
Theorem 3.5.
Let  be a
be a  -pseudo almost automorphic function. Suppose that
-pseudo almost automorphic function. Suppose that  is Lipschitzian in
is Lipschitzian in  uniformly in
uniformly in  ; that is there exists
; that is there exists  such
such

for all  .
.
If  , then
, then  defined by
defined by  belongs to
belongs to  .
.
Proof.
Let  , where
, where  and
and  . Similarly, let
. Similarly, let  , where
, where  and
and  , that is,
, that is,

for all  .
.
It is obvious to see that  . Now decompose
. Now decompose  as follows:
as follows:

Using the theorem of composition of almost automorphic functions, it is easy to see that  . Now, set
. Now, set

Clearly,  . Indeed, we have
. Indeed, we have

and hence for  ,
,

Now using (3.5), it follows that

Using the theorem of composition of functions of  (see [13]) it is easy to see that
(see [13]) it is easy to see that  .
.
Theorem 3.6.
Let  be an
be an  -pseudo almost automorphic function, where
-pseudo almost automorphic function, where  and
and  . Suppose that
. Suppose that  and
and  are uniformly continuous in every bounded subset
are uniformly continuous in every bounded subset  uniformly for
uniformly for  . If
. If  , then
, then  defined by
defined by  belongs to
belongs to  .
.
Proof.
Let  , where
, where  and
and  . Similarly, let
. Similarly, let  , where
, where  and
and  .
.
It is obvious to see that  . Now decompose
. Now decompose  as follows:
as follows:

Using the theorem of composition of almost automorphic functions, it is easy to see that  . Now, set
. Now, set

We claim that  . First of all, note that the uniformly continuity of
. First of all, note that the uniformly continuity of  on bounded subsets
on bounded subsets  yields the uniform continuity of its Bohr transform
yields the uniform continuity of its Bohr transform  on bounded subsets of
on bounded subsets of  . Since both
. Since both  are bounded functions, it follows that there exists
are bounded functions, it follows that there exists  a bounded subset such that
a bounded subset such that  for each
for each  . Now from the uniform continuity of
. Now from the uniform continuity of  on bounded subsets of
on bounded subsets of  , it obviously follows that
, it obviously follows that  is uniformly continuous on
is uniformly continuous on  uniformly for each
uniformly for each  . Therefore for every
. Therefore for every  there exists
there exists  such that for all
such that for all  with
with  yield
yield

Using the proof of the composition theorem [2, Theorem 2.4], (applied to  ) it follows
) it follows

Using the theorem of composition [2, Theorem 2.4] for functions of  it is easy to see that
it is easy to see that  .
.
4. Sectorial Linear Operators
Definition 4.1.
A linear operator  (not necessarily densely defined) is said to be sectorial if the following holds: there exist constants
(not necessarily densely defined) is said to be sectorial if the following holds: there exist constants  ,
,  , and
, and  such that
such that  ,
,

The class of sectorial operators is very rich and contains most of classical operators encountered in literature.
Example 4.2.
Let  and let
and let  be open bounded subset with regular boundary
be open bounded subset with regular boundary  . Let
. Let  be the Lebesgue space.
be the Lebesgue space.
Define the linear operator  as follows:
as follows:

It can be checked that the operator  is sectorial on
is sectorial on  .
.
It is wellknown that [14] if  is sectorial, then it generates an analytic semigroup
is sectorial, then it generates an analytic semigroup  , which maps
, which maps  into
into  and such that there exist
and such that there exist  with
with


Throughout the rest of the paper, we suppose that the semigroup  is hyperbolic; that is, there exist a projection
is hyperbolic; that is, there exist a projection  and constants
and constants  such that
such that  commutes with
commutes with  ,
,  is invariant with respect to
is invariant with respect to  ,
,  is invertible, and the following hold:
is invertible, and the following hold:


where  and, for
and, for  ,
,  .
.
Recall that the analytic semigroup  associated with
associated with  is hyperbolic if and only if
is hyperbolic if and only if

see details in [23, Proposition 1.15, page 305]
Definition 4.3.
Let  . A Banach space
. A Banach space  is said to be an intermediate space between
is said to be an intermediate space between  and
and  , or a space of class
, or a space of class  , if
, if  , and there is a constant
, and there is a constant  such that
such that

where  is the graph norm of
is the graph norm of  .
.
Concrete examples of  include
include  for
for  , the domains of the fractional powers of
, the domains of the fractional powers of  , the real interpolation spaces
, the real interpolation spaces  ,
,  , defined as the space of all
, defined as the space of all  such
such

with the norm

the abstract Hölder spaces  as well as the complex interpolation spaces
as well as the complex interpolation spaces  ; see Lunardi [14] for details.
; see Lunardi [14] for details.
For a hyperbolic analytic semigroup  , one can easily check that similar estimations as both (4.5) and (4.6) still hold with the
, one can easily check that similar estimations as both (4.5) and (4.6) still hold with the  -norms
-norms  . In fact, as the part of
. In fact, as the part of  in
in  is bounded, it follows from (4.6) that
is bounded, it follows from (4.6) that

Hence, from (4.8) there exists a constant  such that
such that

In addition to the above, the following holds:

and hence from (4.5), one obtains

where  depends on
depends on  . For
. For  , by (4.4) and (4.8),
, by (4.4) and (4.8),

Hence, there exist constants  and
and  such that
such that

5. Existence of Pseudo Almost Automorphic Solutions
This section is devoted to the search of an almost automorphic solution to the partial hyperbolic differential equation (1.3).
Definition 5.1.
Let  . A bounded continuous function
. A bounded continuous function  is said to be a mild solution to (1.3) provided that the function
is said to be a mild solution to (1.3) provided that the function  is integrable on
is integrable on  ,
,  is integrable on
is integrable on  for each
for each  and
and

for all  .
.
Throughout the rest of the paper we denote by  and
and  the nonlinear integral operators defined by
the nonlinear integral operators defined by

Let  and let
and let  such that
such that  Throughout the rest of the paper, we suppose that the operator
Throughout the rest of the paper, we suppose that the operator  is sectorial and generates a hyperbolic (analytic) semigroup
is sectorial and generates a hyperbolic (analytic) semigroup  and requires the following assumptions.
and requires the following assumptions.
(H.1)Let  . Then
. Then  , or
, or  , or
, or  , or
, or  . Moreover, we assume that the linear operators
. Moreover, we assume that the linear operators  are bounded.
are bounded.
(H.2)Let  ,
,  be an S p-pseudo almost automorphic function in
be an S p-pseudo almost automorphic function in  uniformly in
uniformly in  , and let
, and let be S p-pseudo almost automorphic in
be S p-pseudo almost automorphic in  uniformly in
uniformly in  . Moreover, the functions
. Moreover, the functions  are uniformly Lipschitz with respect to the second argument in the following sense: there exists
are uniformly Lipschitz with respect to the second argument in the following sense: there exists  such that
such that

for all  and
and  .
.
In order to show that  and
and  are well defined, we need the next lemma whose proof can be found in Diagana [12].
are well defined, we need the next lemma whose proof can be found in Diagana [12].
Lemma 5.2 (see [12]).
Let  . Then
. Then


The proof for the pseudo almost automorphy of  is similar to that of
is similar to that of  and hence will be omitted.
and hence will be omitted.
Lemma 5.3.
Under assumptions (H.1)-(H.2), consider the function  , for
, for  , defined by
, defined by

for each  . If
. If

then  .
.
Remark 5.4.
Note that the assumption  holds in several case. This is in particular the case when
holds in several case. This is in particular the case when  .
.
Proof.
Let  . Since
. Since  , it follows that
, it follows that  . Setting
. Setting  and using Theorem 3.5 it follows that
and using Theorem 3.5 it follows that  . Moreover, using (5.5) it follows that
. Moreover, using (5.5) it follows that

and hence the function  is integrable over
is integrable over  for each
for each  .
.
Let  where
where  and
and  . Define, for all
. Define, for all  the sequence of integral operators
the sequence of integral operators

for each  .
.
Now letting  , it follows that
, it follows that

Using Hölder's inequality and the estimate (5.8), it follows that

Using the assumption  , we then deduce from the well-known Weirstrass theorem that the series
, we then deduce from the well-known Weirstrass theorem that the series  is uniformly convergent on
is uniformly convergent on  . Furthermore,
. Furthermore,

 , and
, and

for each 
We claim that  . Indeed, let
. Indeed, let  be a sequence of real numbers. Since
be a sequence of real numbers. Since  , there exists a subsequence
, there exists a subsequence  of
of  and a function
and a function  such that
such that

Define

Set  for
for  . Then using both Hölder's inequality and (5.5), we obtain
. Then using both Hölder's inequality and (5.5), we obtain

where  , as
, as  .
.
Obviously,

Similarly, we can prove that

Therefore the sequence  for each
for each  , and hence its uniform limit
, and hence its uniform limit  .
.
Let us show that each  . Indeed,
. Indeed,

and hence  , as
, as  . Furthermore, using the assumption
. Furthermore, using the assumption  , we then deduce from the well-known Weirstrass theorem that the series
, we then deduce from the well-known Weirstrass theorem that the series

is uniformly convergent on  . Moreover,
. Moreover,

 , and
, and

for each 
Consequently the uniform limit  ; see [21, Lemma 2.5] . Therefore,
; see [21, Lemma 2.5] . Therefore,  is pseudo almost automorphic.
is pseudo almost automorphic.
The proof for the almost automorphy of  is similar to that of
is similar to that of  and hence will be omitted.
and hence will be omitted.
Lemma 5.5.
Under assumptions (H.1)-(H.2), consider the function  , for
, for  , defined by
, defined by

for each  .
.
If  , then
, then  .
.
Proof.
The proof is similar to that of Lemma 5.3 and hence omitted, though here we make use of the approximation (5.4) rather than (5.5).
Throughout the rest of the paper, the constant  denotes the bound of the embedding
denotes the bound of the embedding  , that is,
, that is,

Theorem 5.6.
Under the previous assumptions and if assumptions (H.1)-(H.2) hold, then the evolution equation (1.3) has a unique pseudo almost automorphic solution whenever  is small enough, that is,
is small enough, that is,

where  .
.
Proof.
In  , define the operator
, define the operator  by setting
by setting

for each  .
.
As we have previously seen, for every  ,
,  . From previous assumptions one can easily see that
. From previous assumptions one can easily see that  is well defined and continuous. Moreover, from Theorem 3.5, Lemma 5.3, and Lemma 5.5 we infer that
is well defined and continuous. Moreover, from Theorem 3.5, Lemma 5.3, and Lemma 5.5 we infer that  maps
maps  into
into  . In particular,
. In particular,  maps
maps  into
into  . To complete the proof one has to show that
. To complete the proof one has to show that  has a unique fixedpoint. Let
has a unique fixedpoint. Let  . It is routine to see that
. It is routine to see that

Therefore, by the Banach fixed-point principle, if  , then
, then  has a unique fixed-point, which obviously is the only pseudo almost automorphic solution to (1.3).
has a unique fixed-point, which obviously is the only pseudo almost automorphic solution to (1.3).
6. Example
Let 
 be an open bounded subset with
be an open bounded subset with  boundary
boundary  , and let
, and let  equipped with its natural topology
equipped with its natural topology  .
.
Define the linear operator appearing in (1.3) as follows:

The operator  defined above is sectorial and hence is the infinitesimal generator of an analytic semigroup
defined above is sectorial and hence is the infinitesimal generator of an analytic semigroup  . Moreover, the semigroup
. Moreover, the semigroup  is hyperbolic as
is hyperbolic as  .
.
Throughout the rest of the paper, for each  , we take
, we take  equipped with its
equipped with its  -norm
-norm  . Moreover, we let
. Moreover, we let  and suppose that
and suppose that  . Letting
. Letting  for all
for all  , one easily sees that both operators are bounded from
, one easily sees that both operators are bounded from  into
into  with
with  .
.
We require the following assumption.
(H.3)Let  , let
, let  be an
be an  -pseudo almost automorphic function in
-pseudo almost automorphic function in  uniformly in
uniformly in  , and let
, and let  be
be  -pseudo almost automorphic in
-pseudo almost automorphic in  uniformly in
uniformly in  . Moreover, the functions
. Moreover, the functions  are uniformly Lipschitz with respect to the second argument in the following sense: there exists
are uniformly Lipschitz with respect to the second argument in the following sense: there exists  such that
such that

for all  and
and  .
.
We have the following.
Theorem 6.1.
Under the previous assumptions including (H.3), then the  -dimensional heat equation (1.1) has a unique pseudo almost automorphic solution
-dimensional heat equation (1.1) has a unique pseudo almost automorphic solution  whenever
whenever  is small enough.
is small enough.
Classical examples of the above-mentioned functions  are given as follows:
are given as follows:

where the functions  are
are  -pseudo almost automorphic.
-pseudo almost automorphic.
In this particular case, the corresponding heat equation, that is,

has a unique pseudo almost automorphic solution  whenever
whenever  is small enough.
is small enough.
References
Liang J, Zhang J, Xiao T-J: Composition of pseudo almost automorphic and asymptotically almost automorphic functions. Journal of Mathematical Analysis and Applications 2008, 340: 1493–1499. 10.1016/j.jmaa.2007.09.065
Xiao T-J, Liang J, Zhang J: Pseudo almost automorphic solutions to semilinear differential equations in banach spaces. Semigroup Forum 2008, 76(3):518–524. 10.1007/s00233-007-9011-y
Bochner S: Continuous mappings of almost automorphic and almost periodic functions. Proceedings of the National Academy of Sciences of the United States of America 1964, 52: 907–910. 10.1073/pnas.52.4.907
Zhang CY: Pseudo-almost-periodic solutions of some differential equations. Journal of Mathematical Analysis and Applications 1994, 151: 62–76.
Zhang CY: Pseudo almost periodic solutions of some differential equations. II. Journal of Mathematical Analysis and Applications 1995, 192: 543–561. 10.1006/jmaa.1995.1189
Zhang CY: Integration of vector-valued pseudo-almost periodic functions. Proceedings of the American Mathematical Society 1994, 121: 167–174. 10.1090/S0002-9939-1994-1186140-8
Diagana T: Existence of pseudo almost automorphic solutions to some abstract differential equations with -pseudo almost automorphic coefficients. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(11):3781–3790. 10.1016/j.na.2008.07.034
Ezzinbi K, Fatajou S, N'Guérékata GM: Pseudo almost automorphic solutions to some neutral partial functional differential equations in banach space. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(1–2):674–684. 10.1016/j.na.2008.10.100
Liang J, N'Guérékata GM, Xiao T-J, Zhang J: Some properties of pseudo-almost automorphic functions and applications to abstract differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(7):2731–2735. 10.1016/j.na.2008.03.061
Boulite S, Maniar L, N'Guérékata GM: Almost automorphic solutions for hyperbolic semilinear evolution equations. Semigroup Forum 2005, 71: 231–240. 10.1007/s00233-005-0524-y
Diagana T, N'Guérékata GM: Pseudo almost periodic mild solutions to hyperbolic evolution equations in intermediate banach spaces. Applicable Analysis 2006, 85(6–7):769–780. 10.1080/00036810600708499
Diagana T: Existence of pseudo almost periodic solutions to some classes of partial hyperbolic evolution equations. Electronic Journal of Qualitative Theory of Differential Equations 2007, 2007(3):1–12.
Diagana T: Pseudo Almost Periodic Functions in Banach Spaces. Nova Science, New York, NY, USA; 2007.
Lunardi A: Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and Their Applications. Volume 16. Birkhäuser, Basel, Switzerland; 1995.
Diagana T, Henríquez N, Hernàndez E: Almost automorphic mild solutions to some partial neutral functional-differential equations and applications. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5):1485–1493. 10.1016/j.na.2007.06.048
Diagana T, N'Guérékata GM: Almost automorphic solutions to some classes of partial evolution equations. Applied Mathematics Letters 2007, 20(4):462–466. 10.1016/j.aml.2006.05.015
Diagana T: Existence and uniqueness of pseudo-almost periodic solutions to some classes of partial evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(2):384–395. 10.1016/j.na.2005.11.031
Diagana T: Existence of almost automorphic solutions to some neutral functional differential equations with infinite delay. Electronic Journal of Differential Equations 2008, 2008(129):1–14.
Pankov A: Bounded and Almost Periodic Solutions of Nonlinear Operator Differential Equations, Mathematics and Its Applications (Soviet Series). Volume 55. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990.
Diagana T: Stepanov-like pseudo almost periodic functions and their applications to differential equations. Communications in Mathematical Analysis 2007, 3(1):9–18.
Diagana T: Stepanov-like pseudo-almost periodicity and its applications to some nonautonomous differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009, 69(12):4277–4285.
N'Guérékata GM, Pankov A: Stepanov-like almost automorphic functions and monotone evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2658–2667. 10.1016/j.na.2007.02.012
Engel KJ, Nagel R: One-Parameter Semigroups for Linear Evolution Equations, Graduate Texts in Mathematics. Volume 194. Springer, New York, NY, USA; 2000.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diagana, T., Agarwal, R. Existence of Pseudo Almost Automorphic Solutions for the Heat Equation with 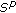 -Pseudo Almost Automorphic Coefficients.
Bound Value Probl 2009, 182527 (2009). https://doi.org/10.1155/2009/182527
-Pseudo Almost Automorphic Coefficients.
Bound Value Probl 2009, 182527 (2009). https://doi.org/10.1155/2009/182527
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/182527
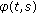 ,
, 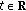 ,
,  , is the Bochner transform of a certain function
, is the Bochner transform of a certain function 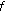 ,
, 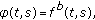 if and only if
if and only if 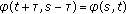 for all
for all  ,
, 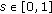 and
and  .
.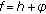 , then
, then 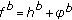 . Moreover,
. Moreover, 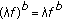 for each scalar
for each scalar  .
.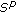 -Pseudo Almost Periodicity
-Pseudo Almost Periodicity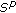 -Almost Automorphy
-Almost Automorphy -Pseudo Almost Automorphy
-Pseudo Almost Automorphy