- Research Article
- Open access
- Published:
Existence and Uniqueness of Smooth Positive Solutions to a Class of Singular 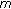 -Point Boundary Value Problems
-Point Boundary Value Problems
Boundary Value Problems volume 2009, Article number: 191627 (2009)
Abstract
This paper investigates the existence and uniqueness of smooth positive solutions to a class of singular m-point boundary value problems of second-order ordinary differential equations. A necessary and sufficient condition for the existence and uniqueness of smooth positive solutions is given by constructing lower and upper solutions and with the maximal theorem. Our nonlinearity  may be singular at
may be singular at  and/or
and/or  .
.
1. Introduction and the Main Results
In this paper,we will consider the existence and uniqueness of positive solutions to a class of second-order singular  -point boundary value problems of the following differential equation:
-point boundary value problems of the following differential equation:

with

where  are constants,
are constants,  and
and  satisfies the following hypothesis:
satisfies the following hypothesis:
 is continuous, nondecreasing on
is continuous, nondecreasing on  , and nonincreasing on
, and nonincreasing on  for each fixed
for each fixed  there exists a real number
there exists a real number  such that for any
such that for any  ,
,

there exists a function  , and
, and  is integrable on
is integrable on  such that
such that

Remark 1.1.
(i) Inequality (1.3) implies

Conversely, (1.5) implies (1.3).
(ii) Inequality (1.4) implies

Conversely, (1.6) implies (1.4).
Remark 1.2.
It follows from (1.3), (1.4) that

When  is increasing with respect to
is increasing with respect to  , singular nonlinear
, singular nonlinear  -point boundary value problems have been extensively studied in the literature, see [1–3]. However, when
-point boundary value problems have been extensively studied in the literature, see [1–3]. However, when  is increasing on
is increasing on  , and is decreasing on
, and is decreasing on  , the study on it has proceeded very slowly. The purpose of this paper is to fill this gap. In addition, it is valuable to point out that the nonlinearity
, the study on it has proceeded very slowly. The purpose of this paper is to fill this gap. In addition, it is valuable to point out that the nonlinearity  may be singular at
may be singular at  and/or
and/or 
When referring to singularity we mean that the functions  in (1.1) are allowed to be unbounded at the points
in (1.1) are allowed to be unbounded at the points  , and/or
, and/or  . A function
. A function  is called a
is called a  (positive) solution to (1.1) and (1.2) if it satisfies (1.1) and (1.2) (
(positive) solution to (1.1) and (1.2) if it satisfies (1.1) and (1.2) ( for
for  ). A
). A  (positive) solution to (1.1) and (1.2) is called a smooth (positive) solution if
(positive) solution to (1.1) and (1.2) is called a smooth (positive) solution if  and
and  both exist (
both exist ( for
for  ). Sometimes, we also call a smooth solution a
). Sometimes, we also call a smooth solution a  solution. It is worth stating here that a nontrivial
solution. It is worth stating here that a nontrivial  nonnegative solution to the problem (1.1), (1.2) must be a positive solution. In fact, it is a nontrivial concave function satisfying (1.2) which, of course, cannot be equal to zero at any point
nonnegative solution to the problem (1.1), (1.2) must be a positive solution. In fact, it is a nontrivial concave function satisfying (1.2) which, of course, cannot be equal to zero at any point 
To seek necessary and sufficient conditions for the existence of solutions to the above problems is important and interesting, but difficult. Thus, researches in this respect are rare up to now. In this paper, we will study the existence and uniqueness of smooth positive solutions to the second-order singular  -point boundary value problem (1.1) and (1.2). A necessary and sufficient condition for the existence of smooth positive solutions is given by constructing lower and upper solutions and with the maximal principle. Also, the uniqueness of the smooth positive solutions is studied.
-point boundary value problem (1.1) and (1.2). A necessary and sufficient condition for the existence of smooth positive solutions is given by constructing lower and upper solutions and with the maximal principle. Also, the uniqueness of the smooth positive solutions is studied.
A function  is called a lower solution to the problem (1.1), (1.2), if
is called a lower solution to the problem (1.1), (1.2), if  and satisfies
and satisfies

Upper solution is defined by reversing the above inequality signs. If there exist a lower solution  and an upper solution
and an upper solution  to problem (1.1), (1.2) such that
to problem (1.1), (1.2) such that  , then
, then  is called a couple of upper and lower solution to problem (1.1), (1.2).
is called a couple of upper and lower solution to problem (1.1), (1.2).
To prove the main result, we need the following maximal principle.
Lemma 1.3 (maximal principle).
Suppose that  , and
, and  . If
. If  such that
such that  then
then 
Proof.
Let


then 
By integrating (1.9) twice and noting (1.10), we have

where

In view of (1.11) and the definition of  , we can obtain
, we can obtain  This completes the proof of Lemma 1.3.
This completes the proof of Lemma 1.3.
Now we state the main results of this paper as follows.
Theorem 1.4.
Suppose that  holds, then a necessary and sufficient condition for the problem (1.1) and (1.2) to have smooth positive solution is that
holds, then a necessary and sufficient condition for the problem (1.1) and (1.2) to have smooth positive solution is that

Theorem 1.5.
Suppose that  and (1.13) hold, then the smooth positive solution to problem (1.1) and (1.2) is also the unique
and (1.13) hold, then the smooth positive solution to problem (1.1) and (1.2) is also the unique  positive solution.
positive solution.
2. Proof of Theorem 1.4
2.1. The Necessary Condition
Suppose that  is a smooth positive solution to the boundary value problem (1.1) and (1.2). We will show that (1.13) holds.
is a smooth positive solution to the boundary value problem (1.1) and (1.2). We will show that (1.13) holds.
It follows from

that  is nonincreasing on
is nonincreasing on  Thus, by the Lebesgue theorem, we have
Thus, by the Lebesgue theorem, we have

It is well known that  can be stated as
can be stated as

where

By (2.3) and (1.2) we have

therefore because of (2.3) and (2.5),

Since  is a smooth positive solution to (1.1) and (1.2), we have
is a smooth positive solution to (1.1) and (1.2), we have

Let  From (2.6), (2.7) it follows that
From (2.6), (2.7) it follows that

Without loss of generality we may assume that  This together with the condition
This together with the condition  implies
implies

On the other hand, notice that  is a smooth positive solution to (1.1), (1.2), we have
is a smooth positive solution to (1.1), (1.2), we have

therefore, there exists a positive number  such that
such that  Obviously,
Obviously,  and
and  It follows from (1.7) that
It follows from (1.7) that

Consequently  which implies that
which implies that

From (2.9) and (2.12) it follows that

which is the required inequality.
2.2. The Existence of Lower and Upper Solutions
Since  is integrable on
is integrable on  thus
thus

Otherwise, if  then there exists a real number
then there exists a real number  such that
such that  when
when  this contradicts with the condition that
this contradicts with the condition that  is integrable on
is integrable on  By condition
By condition  and (2.14) we have
and (2.14) we have


where 
Suppose that (1.13) holds. Let

Since by (1.13), (2.17) we obviously have

and there exists a positive number  such that
such that

By (2.14) and (2.16) we see, if  is sufficiently small, then
is sufficiently small, then

Let

Then from (2.19) and (2.21) we have

Consequently, with the aid of (2.20), (2.22) and the condition  we have
we have


From (2.17), (2.21) it follows that


therefore, (2.23)–(2.26) imply that  are lower and upper solutions to the problem (1.1) and (1.2), respectively.
are lower and upper solutions to the problem (1.1) and (1.2), respectively.
2.3. The Sufficient Condition
First of all, we define a partial ordering in  by
by  if and only if
if and only if

Then, we will define an auxiliary function. For all 

By the assumption of Theorem 1.4, we have that  is continuous.
is continuous.
Let  be a sequence satisfying
be a sequence satisfying  and
and  as
as  and let
and let  be a sequence satisfying
be a sequence satisfying

For each  let us consider the following nonsingular problem:
let us consider the following nonsingular problem:

Obviously, it follows from the proof of Lemma 1.3 that problem (2.30) is equivalent to the integral equation

where  is defined in the proof of Lemma 1.3. It is easy to verify that
is defined in the proof of Lemma 1.3. It is easy to verify that  is a completely continuous operator and
is a completely continuous operator and  is a bounded set. Moreover,
is a bounded set. Moreover,  is a solution to (2.30) if and only if
is a solution to (2.30) if and only if  Using the Schauder's fixed point theorem, we assert that
Using the Schauder's fixed point theorem, we assert that  has at least one fixed point
has at least one fixed point 
We claim that

From this it follows that

Suppose by contradiction that  is not satisfied on
is not satisfied on  . Let
. Let

therefore

Since by the definition of  and (2.30) we obviously have
and (2.30) we obviously have 
Let

So,when  , we have
, we have  and
and

Therefore  that is,
that is,  is an upper convex function in
is an upper convex function in  .
.
By (2.30) and (2.36), for  we have the following two cases:
we have the following two cases:
(i)
(ii)
For case (i): it is clear that  this is a contradiction.
this is a contradiction.
For case (ii): in this case  Since
Since  is decreasing on
is decreasing on  , thus,
, thus,  that is,
that is,  is decreasing on
is decreasing on  From
From  we see
we see  which is in contradiction with
which is in contradiction with 
From this it follows that 
Similarly, we can verify that  Consequently (2.32) holds.
Consequently (2.32) holds.
Using the method of [4] and [5, Theorem  ], we can obtain that there is a
], we can obtain that there is a  positive solution
positive solution  to (1.1), (1.2) such that
to (1.1), (1.2) such that  and a subsequence of
and a subsequence of  converges to
converges to  on any compact subintervals of
on any compact subintervals of 
3. Proof of Theorem 1.5
Suppose that  and
and  are
are  positive solutions to (1.1) and (1.2), and at least one of them is a smooth positive solution. If
positive solutions to (1.1) and (1.2), and at least one of them is a smooth positive solution. If  for any
for any  without loss of generality, we may assume that
without loss of generality, we may assume that  for some
for some  Let
Let

It follows from (3.1) that

By (1.2), it is easy to check that there exist the following two possible cases:
(1)
(2)
Assume that case  holds. By
holds. By  on
on  it is easy to see that
it is easy to see that  exist (finite or
exist (finite or  ), moreover, one of them must be finite. The same conclusion is also valid for
), moreover, one of them must be finite. The same conclusion is also valid for  It follows from (3.2) that
It follows from (3.2) that

consequently

Similarly

From (3.1), (3.4), and (3.5) we have

On the other hand, (3.2), (1.7), and condition  yield
yield

that is,

therefore

From this it follows that

If  on
on  then, by (3.6) we have
then, by (3.6) we have  and then
and then  which imply that there exists a positive number
which imply that there exists a positive number  such that
such that  on
on  It follows from (3.2) that
It follows from (3.2) that  therefore
therefore  Substituting
Substituting  into (1.1) and using condition
into (1.1) and using condition  , we have
, we have

Noticing (3.11) and  we have
we have

which contradicts with the condition that  Therefore,
Therefore,  and
and  on
on  Thus,
Thus,  , which contradicts with (3.6). So case
, which contradicts with (3.6). So case  is impossible.
is impossible.
By analogous methods, we can obtain a contradiction for case  . So
. So  for any
for any  which implies that the result of Theorem 1.5 holds.
which implies that the result of Theorem 1.5 holds.
4. Concerned Remarks and Applications
Remark 4.1.
The typical function satisfying  is
is  where
where 
Remark 4.2.
Condition  includes e-concave function (see [6]) as special case. For example, Liu and Yu [7] consider the existence and uniqueness of positive solution to a class of singular boundary value problem under the following condition:
includes e-concave function (see [6]) as special case. For example, Liu and Yu [7] consider the existence and uniqueness of positive solution to a class of singular boundary value problem under the following condition:

where  and
and  is nondecreasing on
is nondecreasing on  , nonincreasing on
, nonincreasing on  Clearly, condition
Clearly, condition  is weaker than the above condition (4.1).
is weaker than the above condition (4.1).
In fact, for any  from (4.1) it follows that
from (4.1) it follows that

On the other hand, for any  from (4.1) it follows that
from (4.1) it follows that

that is, 
In what follows, by using the results obtained in this paper, we study the boundary value problem

where  We have the following theorem.
We have the following theorem.
Theorem 4.3.
A necessary and sufficient condition for problem (4.4) to have smooth positive solution is that

Moreover, when the positive solution exists, it is unique.
Remark 4.4.
Consider (1.1) and the following singular  -point boundary value conditions:
-point boundary value conditions:

By analogous methods, we have the following results.
Assume that  is a
is a  positive solution to (1.1) and (4.6), then
positive solution to (1.1) and (4.6), then  can be stated
can be stated

where  is defined in (2.4).
is defined in (2.4).
Theorem 4.5.
Suppose that  holds, then a necessary and sufficient condition for the problem (1.1) and (4.6) to have smooth positive solution is that
holds, then a necessary and sufficient condition for the problem (1.1) and (4.6) to have smooth positive solution is that

Theorem 4.6.
Suppose  and (4.8) hold, then the smooth positive solution to problem (1.1) and (4.6) is also unique
and (4.8) hold, then the smooth positive solution to problem (1.1) and (4.6) is also unique  positive solution.
positive solution.
References
Du X, Zhao Z: A necessary and sufficient condition of the existence of positive solutions to singular sublinear three-point boundary value problems. Applied Mathematics and Computation 2007, 186(1):404–413. 10.1016/j.amc.2006.07.120
Du X, Zhao Z: On existence theorems of positive solutions to nonlinear singular differential equations. Applied Mathematics and Computation 2007, 190(1):542–552. 10.1016/j.amc.2007.01.073
Wei Z: A necessary and sufficient condition for the existence of positive solutions of singular super-linear
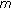 -point boundary value problems. Applied Mathematics and Computation 2006, 179(1):67–78. 10.1016/j.amc.2005.11.077
-point boundary value problems. Applied Mathematics and Computation 2006, 179(1):67–78. 10.1016/j.amc.2005.11.077Zhang Y: Positive solutions of singular sublinear Emden-Fowler boundary value problems. Journal of Mathematical Analysis and Applications 1994, 185(1):215–222. 10.1006/jmaa.1994.1243
Hartman P: Ordinary Differential Equations. 2nd edition. Brikhäuser, Boston, Mass, USA; 1982.
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Liu Y, Yu H: Existence and uniqueness of positive solution for singular boundary value problem. Computers & Mathematics with Applications 2005, 50(1–2):133–143. 10.1016/j.camwa.2005.01.022
Acknowledgment
Research supported by the National Natural Science Foundation of China (10871116), the Natural Science Foundation of Shandong Province (Q2008A03) and the Doctoral Program Foundation of Education Ministry of China (200804460001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Du, X., Zhao, Z. Existence and Uniqueness of Smooth Positive Solutions to a Class of Singular 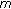 -Point Boundary Value Problems.
Bound Value Probl 2009, 191627 (2009). https://doi.org/10.1155/2009/191627
-Point Boundary Value Problems.
Bound Value Probl 2009, 191627 (2009). https://doi.org/10.1155/2009/191627
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/191627
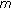 -point boundary value problems. Applied Mathematics and Computation 2006, 179(1):67–78. 10.1016/j.amc.2005.11.077
-point boundary value problems. Applied Mathematics and Computation 2006, 179(1):67–78. 10.1016/j.amc.2005.11.077