- Research Article
- Open access
- Published:
Solving the Axisymmetric Inverse Heat Conduction Problem by a Wavelet Dual Least Squares Method
Boundary Value Problems volume 2009, Article number: 260941 (2009)
Abstract
We consider an axisymmetric inverse heat conduction problem of determining the surface temperature from a fixed location inside a cylinder. This problem is ill-posed; the solution (if it exists) does not depend continuously on the data. A special project method—dual least squares method generated by the family of Shannon wavelet is applied to formulate regularized solution. Meanwhile, an order optimal error estimate between the approximate solution and exact solution is proved.
1. Introduction
Inverse heat conduction problems (IHCP) have become an interesting subject recently, and many regularization methods have been developed for the analysis of IHCP [1–13]. These methods include Tikhonov method [1, 2], mollification method [3, 4], optimal filtering method [5], lines method [6], wavelet and wavelet-Galerkin method [7–11], modified Tikhonov method [12] and "optimal approximations" [13], and so forth. However, most analytical and numerical methods were only used to dealing with IHCP in semiunbounded region. Some works of numerical methods were presented for IHCP in bounded domain [14–19].
Chen et al. [14] applied the hybrid numerical algorithm of Laplace transform technique to the IHCP in a rectangular plate. Busby and Trujillo [15] used the dynamic programming method to investigate the IHCP in a slab. Alifanov and Kerov [16] and Louahlia-Gualous et al. [17] researched IHCP in a cylinder. However to the authors' knowledge, most of them did not give any stability theory and convergence proofs.
In this paper, we will treat with a special IHCP whose physical model consists of an infinitely long cylinder of radius  . It is considered axisymmetric and a thermocouple (measurement equipment of temperature) is installed inside the cylinder (at the radius
. It is considered axisymmetric and a thermocouple (measurement equipment of temperature) is installed inside the cylinder (at the radius  ,
,  ). The correspondingly mathematical model of our problem can be described by the following axisymmetric heat conduction problem:
). The correspondingly mathematical model of our problem can be described by the following axisymmetric heat conduction problem:

where the functions  and
and  belong to
belong to  for every fixed
for every fixed  ,
,  is the radial coordinate,
is the radial coordinate,  denotes the temperature history at one fixed radius
denotes the temperature history at one fixed radius  of cylinder. We want to recover
of cylinder. We want to recover  for
for  . This problem is ill-posed problem; a small perturbation in the data may cause dramatically large errors in the solution
. This problem is ill-posed problem; a small perturbation in the data may cause dramatically large errors in the solution  (The details can be seen in Section 2).
(The details can be seen in Section 2).
To the authors' knowledge, up to now, there is no regularization theory with error estimate for problem (1.1) in the interval  . The major objective of this paper is to do the theoretic stability and convergence estimates for problem (1.1).
. The major objective of this paper is to do the theoretic stability and convergence estimates for problem (1.1).
Xiong and Fu [11] and Regińska [20] solved the sideways heat equation in semi-unbounded region by applying the wavelet dual least squares method, which is based on the family of Meyer wavelet. In this paper, we will apply a wavelet dual least squares method generated by the family of Shannon wavelet to problem (1.1) in bounded domain for determining surface temperature. According to the optimality results of general regularization theory, we conclude that our error estimate on surface temperature is order optimal.
2. Formulation of Solution of Problem (1.1)
As we consider problem (1.1) in  with respect to variable
with respect to variable  , we extend
, we extend  , and other functions of variable
, and other functions of variable  appearing in the paper to be zero for
appearing in the paper to be zero for  . Throughout the paper, we assume that for the exact
. Throughout the paper, we assume that for the exact  the solution
the solution  exists and satisfies an apriori bound
exists and satisfies an apriori bound

where  is defined by
is defined by

Since  is measured by the thermocouple, there will be measurement errors, and we would actually have as data some function
is measured by the thermocouple, there will be measurement errors, and we would actually have as data some function  , for which
, for which

where the constant  represents a bound on the measurement error, and
represents a bound on the measurement error, and  denotes the
denotes the  norm and
norm and

is the Fourier transform of function  . The problem (1.1) can be formulated, in frequency space, as follows:
. The problem (1.1) can be formulated, in frequency space, as follows:



Then we have the following lemma.
Lemma 2.1.
Problem (2.5)–(2.7) has the solution given by

where  denotes modified spherical Bessel function which given by [21]
denotes modified spherical Bessel function which given by [21]

Proof.
Due to [21], we can solve (2.5), in the frequency domain, to obtain

where  denotes also modified spherical Bessel function which is given by
denotes also modified spherical Bessel function which is given by

Combining  with condition(2.7), we obtain
with condition(2.7), we obtain  , that is,
, that is,

According to [21], there holds

where  , both
, both  and
and  denote the Kelvin functions. Since
denote the Kelvin functions. Since  , we have
, we have

Therefore, for  ,
,

Solving the systems (2.6) and (2.12) using (2.15) we get

Substitution of  in (2.16) into (2.12), we obtain (2.8).
in (2.16) into (2.12), we obtain (2.8).
Applying an inverse Fourier transform to (2.8), problem (1.1) has the solution

In order to obtain ill-posedness of problem (1.1) for  , we need the following lemma.
, we need the following lemma.
Lemma 2.2.
If function  satisfies (2.15), then there exist positive constants
satisfies (2.15), then there exist positive constants  such that, for
such that, for 


Proof.
First, due to [21] and (2.15), we have, for  and
and  ,
,

then there exist positive constants  such that, for
such that, for  large enough, say
large enough, say 

From these we know that there exist positive constants  and
and  such that, for
such that, for  and
and  ,
,

Then, since function  is continuous in the closed region
is continuous in the closed region  . Threrfore, there exist constants
. Threrfore, there exist constants  and
and  such that, for
such that, for  and
and  ,
,

Finally, combining inequalities (2.22) with (2.23), we can see that there exist others constants  and
and  such that, for
such that, for  , inequalities (2.18) are valid. Similarly, we obtain inequalities (2.19).
, inequalities (2.18) are valid. Similarly, we obtain inequalities (2.19).
In order to formulate problem (1.1) for  in terms of an operator equation in the space
in terms of an operator equation in the space  , we define an operator
, we define an operator  , that is,
, that is,

From (2.8), we have

Denote  , and we can see that
, and we can see that  is a multiplication operator:
is a multiplication operator:

From (2.26), we can prove the following lemma.
Lemma 2.3.
Let  be the adjoint to
be the adjoint to  , then
, then  corresponds to the following problem where the left-hand side
corresponds to the following problem where the left-hand side  of problem (1.1) is replaced by
of problem (1.1) is replaced by  , says
, says


Proof.
Via the the following relations, combining with (2.26),

we can get the adjoint operator  of
of  in frequency domain
in frequency domain

On the other hand, the problem (2.27) can be formulated, in frequency space, as follows:

Taking the conjugate operator for problem (2.5)–(2.7), we realize that  . Therefore, by Lemma 2.1, we conclude that
. Therefore, by Lemma 2.1, we conclude that

that is,

Hence the conclusion of Lemma 2.3 is proved.
The Parseval formula for the Fourier transform together with inequality (2.18), there holds

This implies that  , which is Fourier transform of exact data
, which is Fourier transform of exact data  , must decay rapidly at high frequencies since
, must decay rapidly at high frequencies since  . But such a decay is not likely to occur in the Fourier transform of the measured noisy data
. But such a decay is not likely to occur in the Fourier transform of the measured noisy data  at
at  . So, small perturbation of
. So, small perturbation of  in high frequency components can blow up and completely destroy the solution
in high frequency components can blow up and completely destroy the solution  given by (2.17) for
given by (2.17) for  .
.
3. Wavelet Dual Least Squares Method
3.1. Dual Least Squares Method
A general projection method for the operator equation  ,
,  is generated by two subspace families
is generated by two subspace families  and
and  of
of  and the approximate solution
and the approximate solution  is defined to be the solution of the following problem:
is defined to be the solution of the following problem:

where  denotes the inner product in
denotes the inner product in  . If
. If  and subspaces
and subspaces  are chosen in such a way that
are chosen in such a way that

Then we have a special case of projection method known as the dual least squares method. If  is an orthogonal basis of
is an orthogonal basis of  and
and  is the solution of the equation
is the solution of the equation

then the approximate solution is explicitly given by the expression

3.2. Shannon Wavelets
In [22], the Shannon scaling function is  and its Fourier transform is
and its Fourier transform is

The corresponding wavelet function  is given by its Fourier transform
is given by its Fourier transform

Let us list some notation:  ,
,  ,
,  ,
,  and
and  for
for  , the index set
, the index set

Because  , hence we can define the subspaces
, hence we can define the subspaces 

Define an orthogonal projection  :
:

then from (3.4) we easily conclude  . From the point of view of an application to the problem (1.1), the important property of Shannon wavelets is the compactness of their support in the frequency space. Indeed, since
. From the point of view of an application to the problem (1.1), the important property of Shannon wavelets is the compactness of their support in the frequency space. Indeed, since

it follows that for any 

From (3.9),  can be seen as a low-pass filter. The frequencies with greater than
can be seen as a low-pass filter. The frequencies with greater than  are filtered away.
are filtered away.
Theorem 3.1.
If  is the solution of problem (1.1) satisfying the condition
is the solution of problem (1.1) satisfying the condition  , then for any fixed
, then for any fixed 

Proof.
From (3.9), we have

Due to Parseval relation and (2.8), (2.19), and (2.1), there holds

Hence the conclusion of Theorem3.1 is proved.
4. Error Estimates via Dual Least Squares Method Approximation
Before giving error estimates, we present firstly subspaces  . According to
. According to  , the subspaces
, the subspaces  are spanned by
are spanned by  , where
, where

 can be determined by solving the following parabolic equation (see Lemma 2.3):
can be determined by solving the following parabolic equation (see Lemma 2.3):

Since  is compact, the solution exists for any
is compact, the solution exists for any  . Similarly the solution of the adjoint equation is unique. Therefore for a given
. Similarly the solution of the adjoint equation is unique. Therefore for a given  ,
,  can be uniquely determined according to (4.2), furthermore
can be uniquely determined according to (4.2), furthermore

The approximate solution for noisy data  is explicitly given by
is explicitly given by

Now we will devote to estimating the error  .
.
Theorem 4.1.
If  is noisy data satisfying the condition
is noisy data satisfying the condition  , then for any fixed
, then for any fixed 

Proof.
From (4.3), we have  . Note that
. Note that  given by (4.4),
given by (4.4),  given by (3.4) and (2.18), for
given by (3.4) and (2.18), for  , there holds
, there holds

Hence the conclusion of Theorem 4.1 is proved.
The following is the main result of this paper.
Theorem 4.2.
Let  be the exact solution of (1.1) and let
be the exact solution of (1.1) and let  be given by (4.4). If
be given by (4.4). If  and
and  is such that
is such that

then for any fixed 

where  .
.
Proof.
Combining Theorem 4.1 with Theorem 3.1, and noting the choice rule (4.7) of  , we can obtain
, we can obtain

Note that

thus, there holds, for 

Hence the conclusion of Theorem 4.2 is proved.
Remark 4.3.
-
(i)
When
 and
and 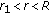 , estimate (4.8) is a Hölder stability estimate given by
, estimate (4.8) is a Hölder stability estimate given by 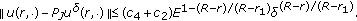 (4.12)
(4.12)
-
(ii)
When
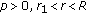 , estimate (4.8) is a logarithmical Hölder stability estimate.
, estimate (4.8) is a logarithmical Hölder stability estimate. -
(iii)
When
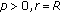 , estimate (4.3) becomes
, estimate (4.3) becomes  (4.13)
(4.13)
This is a logarithmical stability estimate.
Remark 4.4.
In general, the a-priori bound  is unknown in practice, in this case, with
is unknown in practice, in this case, with

then

where  .
.
References
Carasso A: Determining surface temperatures from interior observations. SIAM Journal on Applied Mathematics 1982, 42(3):558–574. 10.1137/0142040
Fu C-L: Simplified Tikhonov and Fourier regularization methods on a general sideways parabolic equation. Journal of Computational and Applied Mathematics 2004, 167(2):449–463. 10.1016/j.cam.2003.10.011
Murio DA: The Mollification Method and the Numerical Solution of Ill-Posed Problems, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+254.
Hào DN, Reinhardt H-J: On a sideways parabolic equation. Inverse Problems 1997, 13(2):297–309. 10.1088/0266-5611/13/2/007
Seidman TI, Eldén L: An 'optimal filtering' method for the sideways heat equation. Inverse Problems 1990, 6(4):681–696. 10.1088/0266-5611/6/4/013
Eldén L: Solving the sideways heat equation by a method of lines. Journal of Heat Transfer 1997, 119: 406–412. 10.1115/1.2824112
Eldén L, Berntsson F, Regińska T: Wavelet and Fourier methods for solving the sideways heat equation. SIAM Journal on Scientific Computing 2000, 21(6):2187–2205. 10.1137/S1064827597331394
Regińska T, Eldén L: Solving the sideways heat equation by a wavelet-Galerkin method. Inverse Problems 1997, 13(4):1093–1106. 10.1088/0266-5611/13/4/014
Regińska T, Eldén L: Stability and convergence of the wavelet-Galerkin method for the sideways heat equation. Journal of Inverse and Ill-Posed Problems 2000, 8(1):31–49.
Fu C-L, Qiu CY: Wavelet and error estimation of surface heat flux. Journal of Computational and Applied Mathematics 2003, 150(1):143–155. 10.1016/S0377-0427(02)00657-X
Xiong X-T, Fu C-L: Determining surface temperature and heat flux by a wavelet dual least squares method. Journal of Computational and Applied Mathematics 2007, 201(1):198–207. 10.1016/j.cam.2006.02.014
Cheng W, Fu C-L, Qian Z: A modified Tikhonov regularization method for a spherically symmetric three-dimensional inverse heat conduction problem. Mathematics and Computers in Simulation 2007, 75(3–4):97–112. 10.1016/j.matcom.2006.09.005
Tautenhahn U: Optimal stable approximations for the sideways heat equation. Journal of Inverse and Ill-Posed Problems 1997, 5(3):287–307. 10.1515/jiip.1997.5.3.287
Chen H-T, Lin S-Y, Fang L-C: Estimation of surface temperature in two-dimensionnal inverse heat conduction problems. International Journal of Heat and Mass Transfer 2001, 44(8):1455–1463. 10.1016/S0017-9310(00)00212-X
Busby HR, Trujillo DM: Numerical soluition to a two-dimensionnal inverse heat conduction problem. International Journal for Numerical Methods in Engineering 1985, 21(2):349–359. 10.1002/nme.1620210211
Alifanov OM, Kerov NV: Determination of external thermal load parameters by solving the two-dimensional inverse heat-conduction problem. Journal of Engineering Physics 1981, 41(4):1049–1053. 10.1007/BF00824760
Louahlia-Gualous H, Panday PK, Artyukhin EA: The inverse determination of the local heat transfer coefficients for nucleate boiling on horizontal cylinder. Journal of Heat Transfer 2003, 125(1):1087–1095.
Hon YC, Wei T: A fundamental solution method for inverse heat conduction problem. Engineering Analysis with Boundary Elements 2004, 28(5):489–495. 10.1016/S0955-7997(03)00102-4
Shidfar A, Pourgholi R: Numerical approximation of solution of an inverse heat conduction problem based on Legendre polynomials. Applied Mathematics and Computation 2006, 175(2):1366–1374. 10.1016/j.amc.2005.08.040
Regińska T: Application of wavelet shrinkage to solving the sideways heat equation. BIT Numerical Mathematics 2001, 41(5):1101–1110. 10.1023/A:1021909816563
Abramowitz M, Stegun IA (Eds): Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Dover, New York, NY, USA; 1972.
Wang JR: The multi-resolution method applied to the sideways heat equation. Journal of Mathematical Analysis and Applications 2005, 309(2):661–673. 10.1016/j.jmaa.2004.11.025
Acknowledgments
The work is supported by the National Natural Science Foundation of China (No. 10671085), the Hight-level Personnel fund of Henan University of Technology (2007BS028), and the Fundamental Research Fund for Natural Science of Education Department of Henan Province of China (No. 2009B110007).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, W., Fu, CL. Solving the Axisymmetric Inverse Heat Conduction Problem by a Wavelet Dual Least Squares Method. Bound Value Probl 2009, 260941 (2009). https://doi.org/10.1155/2009/260941
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/260941
 and
and 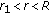 , estimate (4.8) is a Hölder stability estimate given by
, estimate (4.8) is a Hölder stability estimate given by 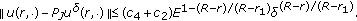
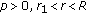 , estimate (4.8) is a logarithmical Hölder stability estimate.
, estimate (4.8) is a logarithmical Hölder stability estimate.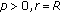 , estimate (4.3) becomes
, estimate (4.3) becomes 