- Research Article
- Open access
- Published:
The Solution of Two-Point Boundary Value Problem of a Class of Duffing-Type Systems with Non-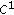 Perturbation Term
Perturbation Term
Boundary Value Problems volume 2009, Article number: 287834 (2009)
Abstract
This paper deals with a two-point boundary value problem of a class of Duffing-type systems with non- perturbation term. Several existence and uniqueness theorems were presented.
perturbation term. Several existence and uniqueness theorems were presented.
1. Introduction
Minimax theorems are one of powerful tools for investigation on the solution of differential equations and differential systems. The investigation on the solution of differential equations and differential systems with non- perturbation term using minimax theorems came into being in the paper of Stepan A.Tersian in 1986 [1]. Tersian proved that the equation
perturbation term using minimax theorems came into being in the paper of Stepan A.Tersian in 1986 [1]. Tersian proved that the equation  exists exactly one generalized solution under the operators
exists exactly one generalized solution under the operators  related to the perturbation term
related to the perturbation term  being selfadjoint and commuting with the operator
being selfadjoint and commuting with the operator  and some other conditions in [1]. Huang Wenhua extended Tersian's theorems in [1] in 2005 and 2006, respectively, and studied the existence and uniqueness of solutions of some differential equations and differential systems with non-
and some other conditions in [1]. Huang Wenhua extended Tersian's theorems in [1] in 2005 and 2006, respectively, and studied the existence and uniqueness of solutions of some differential equations and differential systems with non- perturbation term [2–4], the conditions attached to the non-
perturbation term [2–4], the conditions attached to the non- perturbation term are that the operator
perturbation term are that the operator  related to the term is self-adjoint and commutes with the operator
related to the term is self-adjoint and commutes with the operator  (where
(where  is a selfadjoint operator in the equation
is a selfadjoint operator in the equation  ). Recently, by further research, we observe that the conditions imposed upon
). Recently, by further research, we observe that the conditions imposed upon  can be weakened, the self-adjointness of
can be weakened, the self-adjointness of  can be removed and
can be removed and  is not necessarily commuting with the operator
is not necessarily commuting with the operator  .
.
In this note, we consider a two-point boundary value problem of a class of Duffing-type systems with non- perturbation term and present a result as the operator
perturbation term and present a result as the operator  related to the perturbation term is not necessarily a selfadjoint and commuting with the operator
related to the perturbation term is not necessarily a selfadjoint and commuting with the operator  . We obtain several valuable results in the present paper under the weaker conditions than those in [2–4].
. We obtain several valuable results in the present paper under the weaker conditions than those in [2–4].
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  , respectively, let
, respectively, let  and
and  be two orthogonal closed subspaces of
be two orthogonal closed subspaces of  such that
such that  . Let
. Let  denote the projections from
denote the projections from  to
to  and from
and from  to
to  , respectively. The following theorem will be employed to prove our main theorem.
, respectively. The following theorem will be employed to prove our main theorem.
Theorem 2.1 ([2]).
Let  be a real Hilbert space,
be a real Hilbert space,  an everywhere defined functional with Gâteaux derivative
an everywhere defined functional with Gâteaux derivative  everywhere defined and hemicontinuous. Suppose that there exist two closed subspaces
everywhere defined and hemicontinuous. Suppose that there exist two closed subspaces  and
and  such that
such that  and two nonincreasing functions
and two nonincreasing functions  satisfying
satisfying

and

for all  , and
, and

for all  . Then
. Then
(a) has a unique critical point
has a unique critical point  such that
such that  ;
;
(b) .
.
We also need the following lemma in the present work. To the best of our knowledge, the lemma seems to be new.
Lemma 2.2.
Let  and
and  be two diagonalization
be two diagonalization  matrices, let
matrices, let  and
and  be the eigenvalues of
be the eigenvalues of  and
and  , respectively, where each eigenvalue is repeated according to its multiplicity. If
, respectively, where each eigenvalue is repeated according to its multiplicity. If  commutes with
commutes with  , that is,
, that is,  , then
, then  is a diagonalization matrix and
is a diagonalization matrix and  are the eigenvalues of
are the eigenvalues of  .
.
Proof.
Since  is a diagonalization
is a diagonalization  matrix, there exists an inverse matrix
matrix, there exists an inverse matrix  such that
such that  , where
, where 
 are the distinct eigenvalues of
are the distinct eigenvalues of  ,
,  are the
are the  identity matrices. And since
identity matrices. And since  , that is,
, that is,

we have

Denote  , where
, where  are the submatrices such that
are the submatrices such that  and
and 
 are defined, then, by (2.5),
are defined, then, by (2.5),

Noticed that  , we have
, we have  , and hence
, and hence

where  and
and  are the same order square matrices. Since
are the same order square matrices. Since  is a diagonalization
is a diagonalization  matrix, there exists an invertible matrix
matrix, there exists an invertible matrix  such that
such that

where  are the eigenvalues of
are the eigenvalues of  .
.
Let  , then
, then  is an invertible matrix such that
is an invertible matrix such that  and
and

 is a diagonalization matrix and
is a diagonalization matrix and  are the eigenvalues of
are the eigenvalues of  .
.
The proof of Lemma 2.2 is fulfilled.
Let  denote the usual inner product on
denote the usual inner product on  and denote the corresponding norm by
and denote the corresponding norm by  , where
, where  . Let
. Let  denote the inner product on
denote the inner product on  . It is known very well that
. It is known very well that  is a Hilbert space with inner product
is a Hilbert space with inner product

and norm  , respectively.
, respectively.
Now, we consider the boundary value problem

where  ,
,  is a real constant diagonalization
is a real constant diagonalization  matrix with real eigenvalues
matrix with real eigenvalues  (each eigenvalue is repeated according to its multiplicity),
(each eigenvalue is repeated according to its multiplicity), 
 is a potential Carathéodory vector-valued function ,
is a potential Carathéodory vector-valued function ,  is continuous,
is continuous,  ,
,  ,
,  .
.
Let  ,
,  , then (2.11) may be written in the form
, then (2.11) may be written in the form

where  ,
,  . Clearly,
. Clearly,  is a potential Carathéodory vector-valued function,
is a potential Carathéodory vector-valued function,  . Clearly, if
. Clearly, if  is a solution of (2.12),
is a solution of (2.12),  will be a solution of (2.11).
will be a solution of (2.11).
Assume that there exists a real bounded diagonalization  matrix
matrix  such that for a.e.
such that for a.e.  and
and 

where  ,
,  commutes with
commutes with  and is possessed of real eigenvalues
and is possessed of real eigenvalues  . In the light of Lemma 2.2,
. In the light of Lemma 2.2,  is a diagonalization
is a diagonalization  matrix with real eigenvalues
matrix with real eigenvalues  (each eigenvalue is repeated according to its multiplicity). Assume that there exist positive integers
(each eigenvalue is repeated according to its multiplicity). Assume that there exist positive integers  such that for
such that for 

Let  be
be  linearly independent eigenvectors associated with the eigenvalues
linearly independent eigenvectors associated with the eigenvalues  and let
and let  be the orthonormal vectors obtained by orthonormalizing to the eigenvectors
be the orthonormal vectors obtained by orthonormalizing to the eigenvectors  of
of  . Then for every
. Then for every 

And let the set  be a basis for the space
be a basis for the space  , then for every
, then for every  ,
,

It is well known that each  can be represented by the absolutely convergent Fourier series
can be represented by the absolutely convergent Fourier series

Define the linear operator 

Clearly,  is a selfadjoint operator and
is a selfadjoint operator and  is a Hilbert space for the inner product
is a Hilbert space for the inner product

and the norm induced by the inner product is

Define


Clearly,  and
and  are orthogonal closed subspaces of
are orthogonal closed subspaces of  and
and  .
.
Define two projective mappings  and
and  by
by  and
and  ,
,  , then
, then  is a selfadjoint operator.
is a selfadjoint operator.
Using the Riesz representation theorem , we can define a mapping  by
by

We observe that  in (2.23) is defined implicity. Let
in (2.23) is defined implicity. Let  in (2.23), we have
in (2.23), we have

Clearly,  and hence
and hence  is defined implicity by (2.24). It can be proved that
is defined implicity by (2.24). It can be proved that  is a solution of (2.11) if and only if
is a solution of (2.11) if and only if  satisfies the operator equation
satisfies the operator equation

3. The Main Theorems
Now, we state and prove the following theorem concerning the solution of problem (2.11).
Theorem 3.1.
Assume that there exists a real diagonalization  matrix
matrix  with real eigenvalues
with real eigenvalues  satisfying (2.14) and commuting with
satisfying (2.14) and commuting with  . Denote
. Denote


If

problem (2.11) has a unique solution  , and
, and  satisfies
satisfies  , and
, and

where  is a functional defined in (2.24) and
is a functional defined in (2.24) and  .
.
Proof.
First, by virtue of (2.21) and (2.22), we have



Denote 
By (2.24), (2.13), (3.5), (3.6), (3.7), (3.1), and (3.2), for all  , let
, let  ,
,  ,
,  ,
,  ,
,  ,
,  , we have
, we have

for all  , let
, let  ,
,  ,
,  ,
,  ,
,  ,
,  , we have
, we have

By (3.3),  Clearly,
Clearly,  and
and  are nonincreasing. Now, all the conditions in the Theorem 2.1 are satisfied. By virtue of Theorem 2.1, there exists a unique
are nonincreasing. Now, all the conditions in the Theorem 2.1 are satisfied. By virtue of Theorem 2.1, there exists a unique  such that
such that  and
and  where
where  is a functional defined implicity in (2.24) and
is a functional defined implicity in (2.24) and  .
.  is just a unique solution of (2.12) and
is just a unique solution of (2.12) and  is exactly a unique solution of (2.11). The proof of Theorem 3.1 is completed.
is exactly a unique solution of (2.11). The proof of Theorem 3.1 is completed.
Now, we assume that there exists a positive integer  such that
such that

for  Define
Define




Replace the condition (2.14) by (3.10) and replace (2.21), (2.22), (3.1), and (3.2) by (3.11), (3.12), (3.13), and (3.14), respectively. Using the similar proving techniques in the Theorem 3.1, we can prove the following theorem.
Theorem 3.2.
Assume that there exists a real diagonalization  matrix
matrix  with real eigenvalues
with real eigenvalues  satisfying (2.13) and (3.10) and commuting with
satisfying (2.13) and (3.10) and commuting with  . If the functions
. If the functions  and
and  defined in (3.13) and (3.14) satisfy (3.3), problem (2.11) has a unique solution
defined in (3.13) and (3.14) satisfy (3.3), problem (2.11) has a unique solution  , and
, and satisfies
satisfies and (3.4).
and (3.4).
It is also of interest to the case of  .
.
Corollary 3.3.
Let  ,
,  ,
,  and
and  be as in (2.11). Assume that there exists a real diagonalization
be as in (2.11). Assume that there exists a real diagonalization  matrix
matrix  with real eigenvalues
with real eigenvalues  satisfying (2.13) and
satisfying (2.13) and  Denote
Denote

If  and
and  satisfy (3.3), the problem
satisfy (3.3), the problem

has a unique solution  , and
, and  satisfies
satisfies  and (3.4), where
and (3.4), where  is a functional defined in
is a functional defined in

Corollary 3.4.
Let  ,
,  ,
,  ,
,  , and
, and  be as in Corollary 3.3. The eigenvalues of
be as in Corollary 3.3. The eigenvalues of 
 satisfy
satisfy  Denote
Denote

If  and
and  satisfy (3.3), problem (3.16) has a unique solution
satisfy (3.3), problem (3.16) has a unique solution  , and
, and  satisfies
satisfies  and (3.4), where
and (3.4), where  is a functional defined in (3.17).
is a functional defined in (3.17).
If there exists a  functional
functional  such that
such that  , then (2.13) should be
, then (2.13) should be

where  is just a Hessian of
is just a Hessian of  . In this case, the following corollary follows from Theorem 3.1.
. In this case, the following corollary follows from Theorem 3.1.
Corollary 3.5.
Let the eigenvalues of 
 satisfy (2.14). If
satisfy (2.14). If  and
and  defined in (3.1) and (3.2) satisfy (3.3), problem (2.11)(where
defined in (3.1) and (3.2) satisfy (3.3), problem (2.11)(where  ) has a unique solution
) has a unique solution  , and
, and satisfies
satisfies  and (3.4).
and (3.4).
Using the similar techniques of the present paper, we can also investigate the two-point boundary value problem

where  ,
,  ,
,  ,
,  ,
,  and
and  are as in problem (2.11). The corresponding results are similar to the results in the present paper.
are as in problem (2.11). The corresponding results are similar to the results in the present paper.
The special case of  and
and  in problem (3.20) has been studied by Zhou Ting and Huang Wenhua [5]. Zhou and Huang adopted the techniques different from this paper to achieve their research.
in problem (3.20) has been studied by Zhou Ting and Huang Wenhua [5]. Zhou and Huang adopted the techniques different from this paper to achieve their research.
References
Tersian SA: A minimax theorem and applications to nonresonance problems for semilinear equations. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(7):651–668. 10.1016/0362-546X(86)90125-2
Wenhua H, Zuhe S: Two minimax theorems and the solutions of semilinear equations under the asymptotic non-uniformity conditions. Nonlinear Analysis: Theory, Methods & Applications 2005, 63(8):1199–1214. 10.1016/j.na.2005.02.125
Wenhua H: Minimax theorems and applications to the existence and uniqueness of solutions of some differential equations. Journal of Mathematical Analysis and Applications 2006, 322(2):629–644. 10.1016/j.jmaa.2005.09.046
Wenhua H: A minimax theorem for the quasi-convex functional and the solution of the nonlinear beam equation. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(8):1747–1756. 10.1016/j.na.2005.07.023
Ting Z, Wenhua H: The existence and uniqueness of solution of Duffing equations with non-
 perturbation functional at nonresonance. Boundary Value Problems 2008, 2008:-9.
perturbation functional at nonresonance. Boundary Value Problems 2008, 2008:-9.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhengxian, J., Wenhua, H. The Solution of Two-Point Boundary Value Problem of a Class of Duffing-Type Systems with Non-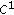 Perturbation Term.
Bound Value Probl 2009, 287834 (2009). https://doi.org/10.1155/2009/287834
Perturbation Term.
Bound Value Probl 2009, 287834 (2009). https://doi.org/10.1155/2009/287834
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/287834
 perturbation functional at nonresonance. Boundary Value Problems 2008, 2008:-9.
perturbation functional at nonresonance. Boundary Value Problems 2008, 2008:-9.