- Research Article
- Open access
- Published:
Existence of Solutions for Fourth-Order Four-Point Boundary Value Problem on Time Scales
Boundary Value Problems volume 2009, Article number: 491952 (2009)
Abstract
We present an existence result for fourth-order four-point boundary value problem on time scales. Our analysis is based on a fixed point theorem due to Krasnoselskii and Zabreiko.
1. Introduction
Very recently, Karaca [1] investigated the following fourth-order four-point boundary value problem on time scales:

for 
 and
and  And the author made the following assumptions:
And the author made the following assumptions:
(A1) and
and 
(A2) If
If  then
then 
The following key lemma is provided in [1].
Lemma 1.1 (see [1, Lemma 2.5]).
Assume that conditions ( ) and (
) and ( ) are satisfied. If
) are satisfied. If  then the boundary value problem
then the boundary value problem

has a unique solution

where


Here 
 , and
, and 
 are given as follows:
are given as follows:

Unfortunately, this lemma is wrong. Without considering the whole interval  the author only considers
the author only considers  in the Green's function
in the Green's function  Thus, the expression of
Thus, the expression of  (1.3) which is a solution to BVP (1.2) is incorrect. In fact, if one takes
(1.3) which is a solution to BVP (1.2) is incorrect. In fact, if one takes 





 then (1.1) reduces to the following boundary value problem:
then (1.1) reduces to the following boundary value problem:

The counterexample is given by [2], from which one can see clearly that [1, Lemma 2.5] is wrong. If one takes  , here
, here  is a constant, then (1.1) reduces to the following fourth-order four-point boundary value problem on time scales:
is a constant, then (1.1) reduces to the following fourth-order four-point boundary value problem on time scales:

The purpose of this paper is to establish some existence criteria of solution for BVP (1.8) which is a special case of (1.1). The paper is organized as follows. In Section 2, some basic time-scale definitions are presented and several preliminary results are given. In Section 3, by employing a fixed point theorem due to Krasnoselskii and Zabreiko, we establish existence of solutions criteria for BVP (1.8). Section 4 is devoted to an example illustrating our main result.
2. Preliminaries
The study of dynamic equations on time scales goes back to its founder Hilger [3] and it is a new area of still fairly theoretical exploration in mathematics. In the recent years boundary value problem on time scales has received considerable attention [4–6]. And an increasing interest in studying the existence of solutions to dynamic equations on time scales is observed, for example, see [7–16].
For convenience, we first recall some definitions and calculus on time scales, so that the paper is self-contained. For the further details concerning the time scales, please see [17–19] which are excellent works for the calculus of time scales.
A time scale  is an arbitrary nonempty closed subset of real numbers
is an arbitrary nonempty closed subset of real numbers  . The operators
. The operators  and
and  from
from  to
to 

are called the forward jump operator and the backward jump operator, respectively.
For all  we assume throughout that
we assume throughout that  has the topology that it inherits from the standard topology on
has the topology that it inherits from the standard topology on  The notations
The notations 
 and so on, will denote time-scale intervals
and so on, will denote time-scale intervals

where  with
with 
Definition 2.1.
Fix  Let
Let  Then we define
Then we define  to be the number (if it exists) with the property that given
to be the number (if it exists) with the property that given  there is a neighborhood
there is a neighborhood  of
of  with
with

Then  is called derivative of
is called derivative of 
Definition 2.2.
If  then we define the integral by
then we define the integral by

We say that a function  is regressive provided
is regressive provided

where  which is called graininess function. If
which is called graininess function. If  is a regressive function, then the generalized exponential function
is a regressive function, then the generalized exponential function  is defined by
is defined by

for 
 is the cylinder transformation, which is defined by
is the cylinder transformation, which is defined by

Let  be two regressive functions, then define
be two regressive functions, then define

The generalized function  has then the following properties.
has then the following properties.
Lemma 2.3 (see [18]).
Assume that  are two regressive functions, then
are two regressive functions, then
(i) and
and 
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
The following well-known fixed point theorem will play a very important role in proving our main result.
Theorem 2.4 (see [20]).
Let  be a Banach space, and let
be a Banach space, and let  be completely continuous. Assume that
be completely continuous. Assume that  is a bounded linear operator such that
is a bounded linear operator such that  is not an eigenvalue of
is not an eigenvalue of  and
and

Then  has a fixed point in
has a fixed point in 
Throughout this paper, let  be endowed with the norm by
be endowed with the norm by

where  And we make the following assumptions:
And we make the following assumptions:
() and
and 
() and
and 

()
Set

For convenience, we denote

First, we present two lemmas about the calculus on Green functions which are crucial in our main results.
Lemma 2.5.
Assume that  and
and  are satisfied. If
are satisfied. If  then
then  is a solution of the following boundary value problem (BVP):
is a solution of the following boundary value problem (BVP):

if and only if

where the Green's function of (2.13) is as follows:

where  are given as (2.12), respectively.
are given as (2.12), respectively.
Proof.
If  is a solution of (2.13), setting
is a solution of (2.13), setting

then it follows from the first equation of (2.13) that

Multiplying (2.17) by  and integrating from
and integrating from  to
to  we get
we get

Similarly, by (2.18), we have

Then substituting (2.18) into (2.19), we get for each  that
that

Substituting this expression for  into the boundary conditions of (2.13). By some calculations, we get
into the boundary conditions of (2.13). By some calculations, we get

Then substituting (2.21) into (2.20), we get

By interchanging the order of integration and some rearrangement of (2.22), we obtain

Thus, we obtain (2.14) consequently.
On the other hand, if  satisfies (2.14), then direct differentiation of (2.14) yields
satisfies (2.14), then direct differentiation of (2.14) yields

And it is easy to know that  and
and  satisfies (2.13).
satisfies (2.13).
Corollary 2.6.
If  then BVP (2.13) reduces to the following problem:
then BVP (2.13) reduces to the following problem:

From Lemma 2.5, BVP (2.25) has a unique solution

where the Green's function of (2.25) is as follows:

where


Proof.
If  is a solution of (2.25), take
is a solution of (2.25), take  then
then 
 Hence, from (2.20) we have
Hence, from (2.20) we have

Substituting this expression for  into the boundary conditions of (2.25). By some calculations, we obtain
into the boundary conditions of (2.25). By some calculations, we obtain

where  is given as (2.28). Then substituting (2.31) into (2.30), we get
is given as (2.28). Then substituting (2.31) into (2.30), we get

where  are as in (2.29), respectively. By some rearrangement of (2.32), we obtain (2.26) consequently.
are as in (2.29), respectively. By some rearrangement of (2.32), we obtain (2.26) consequently.
From the proof of Corollary 2.6, if  take
take 


 we get the following result.
we get the following result.
Corollary 2.7.
The following boundary value problem:

has a unique solution

where the Green's function of (2.33) is as follows:

where

After some rearrangement of (2.35), one obtains

Remark 2.8.
Green function (2.37) associated with BVP (2.33) which is a special case of (2.13) is coincident with part of [21, Lemma 1].
Lemma 2.9.
Assume that conditions ( )–(
)–( ) are satisfied. If
) are satisfied. If  then boundary value problem
then boundary value problem

has a unique solution

where

and  is given in Lemma 2.5.
is given in Lemma 2.5.
Proof.
Consider the following boundary value problem:

The Green's function associated with the BVP (2.41) is  . This completes the proof.
. This completes the proof.
Remark 2.10.
In [1, Lemma 2.5], the solution of (1.2) is defined as

where  and
and  are given as (1.4) and (1.5), respectively. In fact,
are given as (1.4) and (1.5), respectively. In fact,  is incorrect. Thus, we give the right form of
is incorrect. Thus, we give the right form of  as the special case
as the special case  in our Lemma 2.9.
in our Lemma 2.9.
3. Main Results
Theorem 3.1.
Assume ( )–(
)–( ) are satisfied. Moreover, suppose that the following condition is satisfied:
) are satisfied. Moreover, suppose that the following condition is satisfied:
 where
where  are continuous,
are continuous,  with
with

and there exists a continuous nonnegative function  such that
such that  If
If

where

then BVP (1.8) has a solution  .
.
Proof.
Define an operator  by
by

where  is given by (2.40). Then by Lemmas 2.5 and 2.9, it is clear that the fixed points of
is given by (2.40). Then by Lemmas 2.5 and 2.9, it is clear that the fixed points of  are the solutions to the boundary value problem (1.8). First of all, we claim that
are the solutions to the boundary value problem (1.8). First of all, we claim that  is a completely continuous operator, which is divided into 3 steps.
is a completely continuous operator, which is divided into 3 steps.
Step 1 ( is continuous).
is continuous).
Let  be a sequence such that
be a sequence such that  then we have
then we have

Since  are continuous, we have
are continuous, we have  which yields
which yields  That is,
That is,  is continuous.
is continuous.
Step 2 ( maps bounded sets into bounded sets in
maps bounded sets into bounded sets in  ).
).
Let  be a bounded set. Then, for
be a bounded set. Then, for  and any
and any  we have
we have

By virtue of the continuity of  and
and  , we conclude that
, we conclude that  is bounded uniformly, and so
is bounded uniformly, and so  is a bounded set.
is a bounded set.
Step 3 ( maps bounded sets into equicontinuous sets of
maps bounded sets into equicontinuous sets of  ).
).
Let 
 then
then

The right hand side tends to uniformly zero as  Consequently, Steps 1–3 together with the Arzela-Ascoli theorem show that
Consequently, Steps 1–3 together with the Arzela-Ascoli theorem show that  is completely continuous.
is completely continuous.
Now we consider the following boundary value problem:

Define

Obviously,  is a completely continuous bounded linear operator. Moreover, the fixed point of
is a completely continuous bounded linear operator. Moreover, the fixed point of  is a solution of the BVP (3.8) and conversely.
is a solution of the BVP (3.8) and conversely.
We are now in the position to claim that  is not an eigenvalue of
is not an eigenvalue of 
If  and
and  then (3.8) has no nontrivial solution.
then (3.8) has no nontrivial solution.
If  or
or  suppose that the BVP (3.8) has a nontrivial solution
suppose that the BVP (3.8) has a nontrivial solution  and
and  then we have
then we have

which yields

On the other hand, we have

From the above discussion (3.11) and (3.12), we have  . This contradiction implies that boundary value problem (3.8) has no trivial solution. Hence,
. This contradiction implies that boundary value problem (3.8) has no trivial solution. Hence,  is not an eigenvalue of
is not an eigenvalue of 
At last, we show that

By 
 then for any
then for any  there exist a
there exist a  such that
such that

Set  and select
and select  such that
such that 
Denote

Thus for any  and
and  when
when  it follows that
it follows that

In a similar way, we also conclude that for any 

Therefore,

On the other hand, we get

Combining (3.18) with (3.19), we have

Theorem 2.4 guarantees that boundary value problem (1.8) has a solution  It is obvious that
It is obvious that  when
when  for some
for some  In fact, if
In fact, if  then
then  will lead to a contradiction, which completes the proof.
will lead to a contradiction, which completes the proof.
4. Application
We give an example to illustrate our result.
Example 4.1.
Consider the fourth-order four-pint boundary value problem

Notice that  To show that (4.1) has at least one nontrivial solution we apply Theorem 3.1 with
To show that (4.1) has at least one nontrivial solution we apply Theorem 3.1 with 






 and
and  Obviously, (
Obviously, ( )–(
)–( ) are satisfied. And
) are satisfied. And

Since  for each
for each  we have the following.
we have the following.
By simple calculation we have

On the other hand, we notice that

Hence,

That is,  is satisfied. Thus, Theorem 3.1 guarantees that (4.1) has at least one nontrivial solution
is satisfied. Thus, Theorem 3.1 guarantees that (4.1) has at least one nontrivial solution 
References
Karaca IY: Fourth-order four-point boundary value problem on time scales. Applied Mathematics Letters 2008, 21(10):1057–1063. 10.1016/j.aml.2008.01.001
Bai C, Yang D, Zhu H: Existence of solutions for fourth order differential equation with four-point boundary conditions. Applied Mathematics Letters 2007, 20(11):1131–1136. 10.1016/j.aml.2006.11.013
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990, 18(1–2):18–56.
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002, 141(1–2):75–99. 10.1016/S0377-0427(01)00437-X
Benchohra M, Ntouyas SK, Ouahab A: Existence results for second order boundary value problem of impulsive dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004, 296(1):65–73. 10.1016/j.jmaa.2004.02.057
Boey KL, Wong PJY: Positive solutions of two-point right focal boundary value problems on time scales. Computers & Mathematics with Applications 2006, 52(3–4):555–576. 10.1016/j.camwa.2006.08.025
Stehlík P: Periodic boundary value problems on time scales. Advances in Difference Equations 2005, (1):81–92.
Sun J-P: Existence of solution and positive solution of BVP for nonlinear third-order dynamic equation. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(3):629–636. 10.1016/j.na.2005.04.046
Sun H-R, Li W-T: Existence theory for positive solutions to one-dimensional
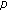 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007, 240(2):217–248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007, 240(2):217–248. 10.1016/j.jde.2007.06.004Su H, Zhang M: Solutions for higher-order dynamic equations on time scales. Applied Mathematics and Computation 2008, 200(1):413–428. 10.1016/j.amc.2007.11.022
Wang D-B, Sun J-P: Existence of a solution and a positive solution of a boundary value problem for a nonlinear fourth-order dynamic equation. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5–6):1817–1823. 10.1016/j.na.2007.07.028
Yaslan İ: Existence results for an even-order boundary value problem on time scales. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):483–491. 10.1016/j.na.2007.12.019
Su Y-H: Multiple positive pseudo-symmetric solutions of
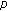 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2009, 49(7–8):1664–1681. 10.1016/j.mcm.2008.10.010
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2009, 49(7–8):1664–1681. 10.1016/j.mcm.2008.10.010Henderson J, Tisdell CC, Yin WKC: Uniqueness implies existence for three-point boundary value problems for dynamic equations. Applied Mathematics Letters 2004, 17(12):1391–1395. 10.1016/j.am1.2003.08.015
Tian Y, Ge W: Existence and uniqueness results for nonlinear first-order three-point boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):2833–2842. 10.1016/j.na.2007.08.054
Anderson DR, Smyrlis G: Solvability for a third-order three-point BVP on time scales. Mathematical and Computer Modelling 2009, 49(9–10):1994–2001. 10.1016/j.mcm.2008.11.009
Agarwal R, Bohner M, O'Regan D, Peterson A: Dynamic equations on time scales: a survey. Journal of Computational and Applied Mathematics 2002, 141(1–2):1–26. 10.1016/S0377-0427(01)00432-0
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Krasnoselskiĭ MA, Zabreĭko PP: Geometrical Methods of Nonlinear Analysis, Grundlehren der Mathematischen Wissenschaften. Volume 263. Springer, Berlin, Germany; 1984:xix+409.
Chai G: Existence of positive solutions for second-order boundary value problem with one parameter. Journal of Mathematical Analysis and Applications 2007, 330(1):541–549. 10.1016/j.jmaa.2006.07.092
Acknowledgments
The authors would like to thank the referees for their valuable suggestions and comments. This work is supported by the National Natural Science Foundation of China (10771212) and the Natural Science Foundation of Jiangsu Education Office (06KJB110010).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, D., Li, G. & Bai, C. Existence of Solutions for Fourth-Order Four-Point Boundary Value Problem on Time Scales. Bound Value Probl 2009, 491952 (2009). https://doi.org/10.1155/2009/491952
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/491952
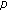 -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007, 240(2):217–248. 10.1016/j.jde.2007.06.004
-Laplacian boundary value problems on time scales. Journal of Differential Equations 2007, 240(2):217–248. 10.1016/j.jde.2007.06.004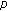 -Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2009, 49(7–8):1664–1681. 10.1016/j.mcm.2008.10.010
-Laplacian dynamic equations on time scales. Mathematical and Computer Modelling 2009, 49(7–8):1664–1681. 10.1016/j.mcm.2008.10.010