- Research Article
- Open access
- Published:
Blowup Analysis for a Semilinear Parabolic System with Nonlocal Boundary Condition
Boundary Value Problems volume 2009, Article number: 516390 (2009)
Abstract
This paper deals with the properties of positive solutions to a semilinear parabolic system with nonlocal boundary condition. We first give the criteria for finite time blowup or global existence, which shows the important influence of nonlocal boundary. And then we establish the precise blowup rate estimate for small weighted nonlocal boundary.
1. Introduction
In this paper, we devote our attention to the singularity analysis of the following semilinear parabolic system:

with nonlocal boundary condition

and initial data

where  is a bounded connected domain with smooth boundary
is a bounded connected domain with smooth boundary  and
and  are positive parameters. Most physical settings lead to the default assumption that the functions
are positive parameters. Most physical settings lead to the default assumption that the functions  defined for
defined for  are nonnegative and continuous, and that the initial data
are nonnegative and continuous, and that the initial data  ,
,  are nonnegative, which are mathematically convenient and currently followed throughout this paper. We also assume that
are nonnegative, which are mathematically convenient and currently followed throughout this paper. We also assume that  satisfies the compatibility condition on
satisfies the compatibility condition on  , and that
, and that  and
and  for any
for any  for the sake of the meaning ofnonlocal boundary.
for the sake of the meaning ofnonlocal boundary.
Over the past few years, a considerable effort has been devoted to studying the blowup properties of solutions to parabolic equations withlocal boundary conditions, say Dirichlet, Neumann, or Robin boundary condition, which can be used to describe heat propagation on the boundary of container (see the survey papers [1, 2]). For example, the system (1.1) and (1.3) with homogeneous Dirichlet boundary condition

has been studied extensively (see [3–5] and references therein), and the following proposition was proved.
Proposition 1.1.
-
(i)
All solutions are global if
 , while there exist both global solutions and finite time blowup solutions depending on the size of initial data when
, while there exist both global solutions and finite time blowup solutions depending on the size of initial data when  (See [4]). (ii) The asymptotic behavior near the blowup time is characterized by
(See [4]). (ii) The asymptotic behavior near the blowup time is characterized by  (1.5)
(1.5)
For the more parabolic problems related to the local boundary, we refer to the recent works [6–9] and references therein.
On the other hand, there are a number of important phenomena modeled by parabolic equations coupled with nonlocal boundary condition of form (1.2). In this case, the solution could be used to describe the entropy per volume of the material [10–12]. Over the past decades, some basic results such as the global existence and decay property have been obtained for the nonlocal boundary problem (1.1)–(1.3) in the case of scalar equation (see [13–16]). In particular, for the blowup solution  of the single equation
of the single equation

under the assumption that  , Seo [15] established the following blowup rate estimate
, Seo [15] established the following blowup rate estimate

for any  . For the more nonlocal boundary problems, we also mention the recent works [17–22]. In particular, Kong and Wang in [17], by using some ideas of Souplet [23], obtained the blowup conditions and blowup profile of the following system:
. For the more nonlocal boundary problems, we also mention the recent works [17–22]. In particular, Kong and Wang in [17], by using some ideas of Souplet [23], obtained the blowup conditions and blowup profile of the following system:

subject to nonlocal boundary (1.2), and Zheng and Kong in [22] gave the condition for global existence or nonexistence of solutions to the following similar system:

with nonlocal boundary condition (1.2). The typical characterization of systems (1.8) and (1.9) is the complete couple of the nonlocal sources, which leads to the analysis of simultaneous blowup.
To our surprise, however, it seems that there is no work dealing with singularity analysis of the parabolic system (1.1) with nonlocal boundary condition (1.2) except for the single equation case, although this is a very classical model. Therefore, the basic motivation for the work under consideration was our desire to understand the role of weight function in the blowup properties of that nonlinear system. We first remark by the standard theory [4, 13] that there exist local nonnegative classical solutions to this system.
Our main results read as follows.
Theorem 1.2.
Suppose that  . All solutions to (1.1)–(1.3) exist globally.
. All solutions to (1.1)–(1.3) exist globally.
It follows from Theorem 1.2 and Proposition 1.1(i) that any weight perturbation on the boundary has no influence on the global existence when  , while the following theorem shows that it plays an important role when
, while the following theorem shows that it plays an important role when  . In particular, Theorem 1.3(ii) is completely different from the case of the local boundary (1.4) (by comparing with Proposition 1.1(i)).
. In particular, Theorem 1.3(ii) is completely different from the case of the local boundary (1.4) (by comparing with Proposition 1.1(i)).
Theorem 1.3.
Suppose that  .
.
-
(i)
For any nonnegative
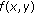 and
and 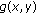 , solutions to (1.1)–(1.3) blow up in finite time provided that the initial data are large enough.
, solutions to (1.1)–(1.3) blow up in finite time provided that the initial data are large enough. -
(ii)
If
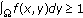 ,
, 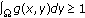 for any
for any 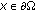 , then any solutions to (1.1)–(1.3) with positive initial data blow up in finite time.
, then any solutions to (1.1)–(1.3) with positive initial data blow up in finite time. -
(iii)
If
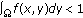 ,
, 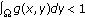 for any
for any  , then solutions to (1.1)–(1.3) with small initial data exist globally in time.
, then solutions to (1.1)–(1.3) with small initial data exist globally in time.
Once we have characterized for which exponents and weights the solution to problem (1.1)–(1.3) can or cannot blow up, we want to study the way the blowing up solutions behave as approaching the blowup time. To this purpose, the first step usually consists in deriving a bound for the blowup rate. For this bound estimate, we will use the classical method initially proposed in Friedman and McLeod [24]. The use of the maximum principle in that process forces us to give the following hypothesis technically.
(H)There exists a constant , such that
, such that
However, it seems that such an assumption is necessary to obtain the estimates of type (1.5) or (1.10) unless some additional restrictions on parameters  are imposed (for the related problem, we refer to the recent work of Matano and Merle [25]).
are imposed (for the related problem, we refer to the recent work of Matano and Merle [25]).
Here to obtain the precise blowup rates, we shall devote to establishing some relationship between the two components  and
and  as our problem involves a system, but we encounter the typical difficulties arising from the integral boundary condition. The following theorem shows that we have partially succeeded in this precise blowup characterization.
as our problem involves a system, but we encounter the typical difficulties arising from the integral boundary condition. The following theorem shows that we have partially succeeded in this precise blowup characterization.
Theorem 1.4.
Suppose that  ,
,  ,
,  ,
,  and assumption (H) holds. If the solution
and assumption (H) holds. If the solution  of (1.1)–(1.3) with positive initial data
of (1.1)–(1.3) with positive initial data  blows up in finite time
blows up in finite time  , then
, then

where  are both positive constants.
are both positive constants.
Remark 1.5.
If  and
and  , then Theorem 1.4 implies that for the blowup solution of problem (1.6), we have the following precise blowup rate estimate:
, then Theorem 1.4 implies that for the blowup solution of problem (1.6), we have the following precise blowup rate estimate:

which improves the estimate (1.7). Moreover, we relax the restriction on  .
.
Remark 1.6.
By comparing with Proposition 1.1(ii), Theorem 1.4 could be explained as the small perturbation of homogeneous Dirichlet boundary, which leads to the appearance of blowup, does not influence the precise asymptotic behavior of solutions near the blowup time and the blowup rate exponents  and
and  are just determined by the corresponding ODE system
are just determined by the corresponding ODE system  . Similar phenomena are also noticed in our previous work [18], where the single porous medium equation is studied.
. Similar phenomena are also noticed in our previous work [18], where the single porous medium equation is studied.
The rest of this paper is organized as follows. Section 2 is devoted to some preliminaries, which include the comparison principle related to system (1.1)–(1.3). In Section 3, we will study the conditions for the solution to blow up and exist globally and hence prove Theorems 1.2 and 1.3. Proof of Theorem 1.4 is given in Section 4.
2. Preliminaries
In this section, we give some basic preliminaries. For convenience, we denote  We begin with the definition of the super- and subsolution of system (1.1)–(1.3).
We begin with the definition of the super- and subsolution of system (1.1)–(1.3).
Definition 2.1.
A pair of functions  is called a subsolution of (1.1)–(1.3) if
is called a subsolution of (1.1)–(1.3) if

A supersolution is defined with each inequality reversed.
Lemma 2.2.
Suppose that  and
and  are nonnegative functions. If
are nonnegative functions. If  satisfy
satisfy

then  on
on  .
.
Proof.
Set  . Since
. Since  , by continuity, there exists
, by continuity, there exists  such that
such that  for all
for all  . Thus
. Thus  .
.
We claim that  will lead to a contradiction. Indeed,
will lead to a contradiction. Indeed,  suggests that
suggests that  or
or  for some
for some  . Without loss of generality, we suppose that
. Without loss of generality, we suppose that  .
.
If  , we first notice that
, we first notice that

In addition, it is clear that  on boundary
on boundary  and at the initial state
and at the initial state  . Then it follows from the strong maximum principle that
. Then it follows from the strong maximum principle that  in
in  , which contradicts to
, which contradicts to  .
.
If  , we shall have a contradiction:
, we shall have a contradiction:

In the last inequality, we have used the facts that  for any
for any  and
and  for any
for any  , which is a direct result of the previous case.
, which is a direct result of the previous case.
Therefore, the claim is true and thus  , which implies that
, which implies that  on
on  .
.
Remark 2.3.
If  and
and  for any
for any  in Lemma 2.2, we can obtain
in Lemma 2.2, we can obtain  in
in  under the assumption that
under the assumption that  for
for  . Indeed, for any
. Indeed, for any  , we can conclude that
, we can conclude that  in
in  as the proof of Lemma 2.2. Then the desired result follows from the limit procedure
as the proof of Lemma 2.2. Then the desired result follows from the limit procedure  .
.
From the above lemma, we can obtain the following comparison principle by the standard argument.
Proposition 2.4.
Let  ) and
) and  be a subsolution and supersolution of (1.1)–(1.3) in
be a subsolution and supersolution of (1.1)–(1.3) in  , respectively. If
, respectively. If  for
for  , then
, then  in
in  .
.
3. Global Existence and Blowup in Finite Time
In this section, we will use the super and subsolution technique to get the global existence or finite time blowup of the solution to (1.1)–(1.3).
Proof of Theorem 1.2.
As  , there exist
, there exist  such that
such that

Then we let  (
( ) be a continuous function satisfying
) be a continuous function satisfying  and set
and set

We consider the following auxiliary problem:

where  is the measure of
is the measure of  and
and  . It follows from [13, Theorem
. It follows from [13, Theorem  ] that
] that  exists globally, and indeed
exists globally, and indeed  (see [13, Theorem
(see [13, Theorem  ]).
]).
Our intention is to show that  is a global supersolution of (1.1)–(1.3). Indeed, a direct computation yields
is a global supersolution of (1.1)–(1.3). Indeed, a direct computation yields

and thus

Here we have used the conclusion  and inequality (3.1). We still have to consider the boundary and initial conditions. When
and inequality (3.1). We still have to consider the boundary and initial conditions. When  , in view of Hölder's inequality, we have
, in view of Hölder's inequality, we have

Similarly, we have also for  that
that

It is clear that  and
and  . Therefore, we get
. Therefore, we get  is a global supersolution of (1.1)–(1.3) and hence the solution to (1.1)–(1.3) exists globally by Proposition 2.4.
is a global supersolution of (1.1)–(1.3) and hence the solution to (1.1)–(1.3) exists globally by Proposition 2.4.
Proof of Theorem 1.3.
-
(i)
Let
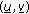 be the solution to the homogeneous Dirichlet boundary problem (1.1), (1.4), and (1.3). Then it is well known that for sufficiently large initial data the solution
be the solution to the homogeneous Dirichlet boundary problem (1.1), (1.4), and (1.3). Then it is well known that for sufficiently large initial data the solution 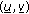 blows up in finite time when
blows up in finite time when 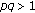 (see [4]). On the other hand, it is obvious that
(see [4]). On the other hand, it is obvious that 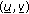 is a subsolution of problem (1.1)–(1.3). Henceforth, the solution of (1.1)–(1.3) with large initial data blows up in finite time provided that
is a subsolution of problem (1.1)–(1.3). Henceforth, the solution of (1.1)–(1.3) with large initial data blows up in finite time provided that 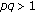 .
. -
(ii)
We consider the ODE system:

where  . Then
. Then  implies that
implies that  blows up in finite time
blows up in finite time  (see [26]). Under the assumption that
(see [26]). Under the assumption that  and
and  for any
for any  ,
,  is a subsolution of problem (1.1)–(1.3). Therefore, by Proposition 2.4, we see that the solution
is a subsolution of problem (1.1)–(1.3). Therefore, by Proposition 2.4, we see that the solution  of problem (1.1)–(1.3) satisfies
of problem (1.1)–(1.3) satisfies  and then
and then  blows up in finite time.
blows up in finite time.
-
(iii)
Let
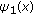 be the positive solution of the linear elliptic problem:
be the positive solution of the linear elliptic problem:

and let  be the positive solution of the linear elliptic problem:
be the positive solution of the linear elliptic problem:

where  is a positive constant such that
is a positive constant such that  . We remark that
. We remark that  and
and  ensure the existence of such
ensure the existence of such  .
.
Let

where  . We now show that
. We now show that  is a supsolution of problem (1.1)–(1.3) for small initial data
is a supsolution of problem (1.1)–(1.3) for small initial data  . Indeed, it follows from
. Indeed, it follows from  that, for
that, for  ,
,

When  ,
,

Here we used  . The above inequalities show that
. The above inequalities show that  is a supsolution of problem (1.1)–(1.3) whenever
is a supsolution of problem (1.1)–(1.3) whenever  . Therefore, system (1.1)–(1.3) has global solutions if
. Therefore, system (1.1)–(1.3) has global solutions if  and
and  ,
,  for any
for any  .
.
4. Blowup Rate Estimate
In this section, we derive the precise blowup rate estimate. To this end, we first establish a partial relationship between the solution components  and
and  , which will be very useful in the subsequent analysis. For definiteness, we may assume
, which will be very useful in the subsequent analysis. For definiteness, we may assume  . If
. If  , we can proceed in the same way by changing the role of
, we can proceed in the same way by changing the role of  and
and  and then obtain the corresponding conclusion.
and then obtain the corresponding conclusion.
Lemma 4.1.
If  ,
,  and
and  for any
for any  , there exists a positive constant
, there exists a positive constant  such that the solution
such that the solution  of problem (1.1)–(1.3) with positive initial data
of problem (1.1)–(1.3) with positive initial data  satisfies
satisfies

Proof.
Let  , where
, where  is a positive constant to be chosen. For
is a positive constant to be chosen. For  , a series of calculations show that
, a series of calculations show that

If we choose  such that
such that  , we have
, we have

where  is a function of
is a function of  and
and  and lies between
and lies between  and
and  .
.
When  , on the other hand, we have
, on the other hand, we have

Denote  ,
,  . Since
. Since  for any
for any  ,
,  . It follows from Jensen's inequality,
. It follows from Jensen's inequality,  and
and  that
that

which implies that

For the initial condition, we have

provided that  .
.
Summarily, if we take  , then it follows from Theorem
, then it follows from Theorem  in [13] that
in [13] that  , that is,
, that is,

which is desired.
Using this lemma, we could establish our blowup rate estimate. To derive our conclusion, we shall use some ideas of [3].
Proof of Theorem 1.4.
For simplicity, we introduce  . Let
. Let  and
and  . A direct computation yields
. A direct computation yields

For  , we have from the boundary conditions that
, we have from the boundary conditions that

It follows from  and Jensen's inequality that the difference in the last brace is nonnegative and thus
and Jensen's inequality that the difference in the last brace is nonnegative and thus

By similar arguments, we have

On the other hand, the hypothesis (H) implies that

Hence, from (4.9)–(4.13) and the comparison principle (see Remark 2.3), we get

That is,

Let  Then
Then  and
and  are Lipschitz continuous and thus are differential almost everywhere (see e.g., [24]). Moreover, we have from equations (1.1) that
are Lipschitz continuous and thus are differential almost everywhere (see e.g., [24]). Moreover, we have from equations (1.1) that

We claim that

for some positive constant  . Indeed, if we let
. Indeed, if we let  be the points at which
be the points at which  attains its maximum, then relation (4.1) means that
attains its maximum, then relation (4.1) means that

At any point  of differentiability of
of differentiability of  , if
, if  ,
,

From (4.15), (4.18), and (4.19), we can confirm our claim (4.17).
Integrating (4.17) on  yields
yields

which gives the upper estimate for  . Namely, there exists a constant
. Namely, there exists a constant  such that
such that

Then by (4.16) and (4.21), we get

Integrating this equality from  to
to  , we obtain
, we obtain

for some positive constant  . Thus we have established the upper estimates for
. Thus we have established the upper estimates for  .
.
To obtain the lower estimate for  , we notice that (4.16) and (4.18) lead to
, we notice that (4.16) and (4.18) lead to

for a constant  . Integrating above equality on
. Integrating above equality on  , we see there exists a positive constant
, we see there exists a positive constant  such that
such that

Finally, we give the lower estimate for  . Indeed, using the relationship (4.16), (4.23) and (4.25), we could prove that
. Indeed, using the relationship (4.16), (4.23) and (4.25), we could prove that  is bounded from below; that is, there exists a positive constant
is bounded from below; that is, there exists a positive constant  such that
such that

To see this, our approach is based on the contradiction arguments. Assume that there would exist two sequences  with
with  and
and  with
with  as
as  such that
such that

Then we could choose a corresponding sequence  such that
such that  , where
, where  is a positive constant to be determined later. As
is a positive constant to be determined later. As  , we have
, we have

From (4.23) and (4.27), we obtain

Choosing  such that
such that  , one can get
, one can get

which would contradict to (4.25) as  is large enough since
is large enough since  as
as  .
.
References
Deng K, Levine HA: The role of critical exponents in blow-up theorems: the sequel. Journal of Mathematical Analysis and Applications 2000, 243(1):85–126. 10.1006/jmaa.1999.6663
Levine HA: The role of critical exponents in blowup theorems. SIAM Review 1990, 32(2):262–288. 10.1137/1032046
Deng K: Blow-up rates for parabolic systems. Zeitschrift für Angewandte Mathematik und Physik 1996, 47(1):132–143. 10.1007/BF00917578
Escobedo M, Herrero MA: A semilinear parabolic system in a bounded domain. Annali di Matematica Pura ed Applicata 1993, 165: 315–336. 10.1007/BF01765854
Wang MX: Blow-up rate estimates for semilinear parabolic systems. Journal of Differential Equations 2001, 170(2):317–324. 10.1006/jdeq.2000.3823
Li FQ: On initial boundary value problems with equivalued surface for nonlinear parabolic equations. Boundary Value Problems 2009, 2009:-23.
Xiang ZY, Mu CL: Blowup behaviors for degenerate parabolic equations coupled via nonlinear boundary flux. Communications on Pure and Applied Analysis 2007, 6(2):487–503.
Xiang ZY: Global existence and nonexistence for degenerate parabolic equations with nonlinear boundary flux. preprint
Xiang ZY: Global existence and nonexistence for diffusive polytropic filtration equations with nonlinear boundary conditions. Zeitschrift für Angewandte Mathematik und Physik. In press
Day WA: A decreasing property of solutions of parabolic equations with applications to thermoelasticity. Quarterly of Applied Mathematics 1983, 40(4):468–475.
Day WA: Heat Conduction within Linear Thermoelasticity, Springer Tracts in Natural Philosophy. Volume 30. Springer, New York, NY, USA; 1985:viii+83.
Friedman A: Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions. Quarterly of Applied Mathematics 1986, 44(3):401–407.
Deng K: Comparison principle for some nonlocal problems. Quarterly of Applied Mathematics 1992, 50(3):517–522.
Pao CV: Asymptotic behavior of solutions of reaction-diffusion equations with nonlocal boundary conditions. Journal of Computational and Applied Mathematics 1998, 88(1):225–238. 10.1016/S0377-0427(97)00215-X
Seo S: Blowup of solutions to heat equations with nonlocal boundary conditions. Kobe Journal of Mathematics 1996, 13(2):123–132.
Seo S: Global existence and decreasing property of boundary values of solutions to parabolic equations with nonlocal boundary conditions. Pacific Journal of Mathematics 2000, 193(1):219–226. 10.2140/pjm.2000.193.219
Kong L-H, Wang M-X: Global existence and blow-up of solutions to a parabolic system with nonlocal sources and boundaries. Science in China. Series A 2007, 50(9):1251–1266. 10.1007/s11425-007-0105-5
Wang YL, Mu CL, Xiang ZY: Blowup of solutions to a porous medium equation with nonlocal boundary condition. Applied Mathematics and Computation 2007, 192(2):579–585. 10.1016/j.amc.2007.03.036
Wang YL, Mu CL, Xiang ZY: Properties of positive solution for nonlocal reaction-diffusion equation with nonlocal boundary. Boundary Value Problems 2007, 2007:-12.
Yin H-M: On a class of parabolic equations with nonlocal boundary conditions. Journal of Mathematical Analysis and Applications 2004, 294(2):712–728. 10.1016/j.jmaa.2004.03.021
Yin YF: On nonlinear parabolic equations with nonlocal boundary condition. Journal of Mathematical Analysis and Applications 1994, 185(1):161–174. 10.1006/jmaa.1994.1239
Zheng S, Kong L: Roles of weight functions in a nonlinear nonlocal parabolic system. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(8):2406–2416. 10.1016/j.na.2007.01.067
Souplet P: Uniform blow-up profiles and boundary behavior for diffusion equations with nonlocal nonlinear source. Journal of Differential Equations 1999, 153(2):374–406. 10.1006/jdeq.1998.3535
Friedman A, McLeod B: Blow-up of positive solutions of semilinear heat equations. Indiana University Mathematics Journal 1985, 34(2):425–447. 10.1512/iumj.1985.34.34025
Matano H, Merle F: Classification of type I and type II behaviors for a supercritical nonlinear heat equation. Journal of Functional Analysis 2009, 256(4):992–1064. 10.1016/j.jfa.2008.05.021
Xiang ZY, Hu XG, Mu CL: Neumann problem for reaction-diffusion systems with nonlocal nonlinear sources. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(7):1209–1224. 10.1016/j.na.2005.01.098
Acknowledgments
The authors are very grateful to the anonymous referees for their careful reading and useful suggestions, which greatly improved the presentation of the paper. This work is supported in part by Natural Science Foundation Project of CQ CSTC (2007BB2450), China Postdoctoral Science Foundation, the Key Scientific Research Foundation of Xihua University, and Youth Foundation of Science and Technology of UESTC.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Xiang, Z. Blowup Analysis for a Semilinear Parabolic System with Nonlocal Boundary Condition. Bound Value Probl 2009, 516390 (2009). https://doi.org/10.1155/2009/516390
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/516390
 , while there exist both global solutions and finite time blowup solutions depending on the size of initial data when
, while there exist both global solutions and finite time blowup solutions depending on the size of initial data when  (See [
(See [
 (See [
(See [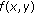 and
and 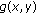 , solutions to (1.1)–(1.3) blow up in finite time provided that the initial data are large enough.
, solutions to (1.1)–(1.3) blow up in finite time provided that the initial data are large enough.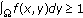 ,
, 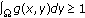 for any
for any 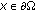 , then any solutions to (1.1)–(1.3) with positive initial data blow up in finite time.
, then any solutions to (1.1)–(1.3) with positive initial data blow up in finite time.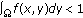 ,
, 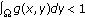 for any
for any  , then solutions to (1.1)–(1.3) with small initial data exist globally in time.
, then solutions to (1.1)–(1.3) with small initial data exist globally in time.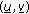 be the solution to the homogeneous Dirichlet boundary problem (1.1), (1.4), and (1.3). Then it is well known that for sufficiently large initial data the solution
be the solution to the homogeneous Dirichlet boundary problem (1.1), (1.4), and (1.3). Then it is well known that for sufficiently large initial data the solution 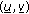 blows up in finite time when
blows up in finite time when 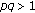 (see [
(see [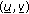 is a subsolution of problem (1.1)–(1.3). Henceforth, the solution of (1.1)–(1.3) with large initial data blows up in finite time provided that
is a subsolution of problem (1.1)–(1.3). Henceforth, the solution of (1.1)–(1.3) with large initial data blows up in finite time provided that 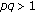 .
.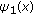 be the positive solution of the linear elliptic problem:
be the positive solution of the linear elliptic problem: