- Research Article
- Open access
- Published:
Existence of Solutions for Fractional Differential Inclusions with Antiperiodic Boundary Conditions
Boundary Value Problems volume 2009, Article number: 625347 (2009)
Abstract
We study the existence of solutions for a class of fractional differential inclusions with anti-periodic boundary conditions. The main result of the paper is based on Bohnenblust- Karlins fixed point theorem. Some applications of the main result are also discussed.
1. Introduction
In some cases and real world problems, fractional-order models are found to be more adequate than integer-order models as fractional derivatives provide an excellent tool for the description of memory and hereditary properties of various materials and processes. The mathematical modelling of systems and processes in the fields of physics, chemistry, aerodynamics, electro dynamics of complex medium, polymer rheology, and so forth, involves derivatives of fractional order. In consequence, the subject of fractional differential equations is gaining much importance and attention. For details and examples, see [1–14] and the references therein.
Antiperiodic boundary value problems have recently received considerable attention as antiperiodic boundary conditions appear in numerous situations, for instance, see [15–22].
Differential inclusions arise in the mathematical modelling of certain problems in economics, optimal control, and so forth. and are widely studied by many authors, see [23–27] and the references therein. For some recent development on differential inclusions, we refer the reader to the references [28–32].
Chang and Nieto [33] discussed the existence of solutions for the fractional boundary value problem:

In this paper, we consider the following fractional differential inclusions with antiperiodic boundary conditions

where  denotes the Caputo fractional derivative of order
denotes the Caputo fractional derivative of order  ,
,  Bohnenblust-Karlin fixed point theorem is applied to prove the existence of solutions of (1.2).
Bohnenblust-Karlin fixed point theorem is applied to prove the existence of solutions of (1.2).
2. Preliminaries
Let  denote a Banach space of continuous functions from
denote a Banach space of continuous functions from  into
into  with the norm
with the norm  Let
Let  be the Banach space of functions
be the Banach space of functions  which are Lebesgue integrable and normed by
which are Lebesgue integrable and normed by 
Now we recall some basic definitions on multivalued maps [34, 35].
Let  be a Banach space. Then a multivalued map
be a Banach space. Then a multivalued map  is convex (closed) valued if
is convex (closed) valued if  is convex (closed) for all
is convex (closed) for all  The map
The map  is bounded on bounded sets if
is bounded on bounded sets if  is bounded in
is bounded in  for any bounded set
for any bounded set  of
of  (i.e.,
(i.e.,  .
.  is called upper semicontinuous (u.s.c.) on
is called upper semicontinuous (u.s.c.) on  if for each
if for each  the set
the set  is a nonempty closed subset of
is a nonempty closed subset of  , and if for each open set
, and if for each open set  of
of  containing
containing  there exists an open neighborhood
there exists an open neighborhood  of
of  such that
such that  .
.  is said to be completely continuous if
is said to be completely continuous if  is relatively compact for every bounded subset
is relatively compact for every bounded subset  of
of  If the multivalued map
If the multivalued map  is completely continuous with nonempty compact values, then
is completely continuous with nonempty compact values, then  is u.s.c. if and only if
is u.s.c. if and only if  has a closed graph, that is,
has a closed graph, that is,  imply
imply  In the following study,
In the following study,  denotes the set of all nonempty bounded, closed, and convex subset of
denotes the set of all nonempty bounded, closed, and convex subset of  .
.  has a fixed point if there is
has a fixed point if there is  such that
such that 
Let us record some definitions on fractional calculus [8, 11, 13].
Definition 2.1.
For a function  the Caputo derivative of fractional order
the Caputo derivative of fractional order  is defined as
is defined as

where  denotes the integer part of the real number
denotes the integer part of the real number  and
and  denotes the gamma function.
denotes the gamma function.
Definition 2.2.
The Riemann-Liouville fractional integral of order  for a function
for a function  is defined as
is defined as

provided the right-hand side is pointwise defined on 
Definition 2.3.
The Riemann-Liouville fractional derivative of order  for a function
for a function  is defined by
is defined by

provided the right-hand side is pointwise defined on 
In passing, we remark that the Caputo derivative becomes the conventional  derivative of the function as
derivative of the function as  and the initial conditions for fractional differential equations retain the same form as that of ordinary differential equations with integer derivatives. On the other hand, the Riemann-Liouville fractional derivative could hardly produce the physical interpretation of the initial conditions required for the initial value problems involving fractional differential equations (the same applies to the boundary value problems of fractional differential equations). Moreover, the Caputo derivative for a constant is zero while the Riemann-Liouville fractional derivative of a constant is nonzero. For more details, see [13].
and the initial conditions for fractional differential equations retain the same form as that of ordinary differential equations with integer derivatives. On the other hand, the Riemann-Liouville fractional derivative could hardly produce the physical interpretation of the initial conditions required for the initial value problems involving fractional differential equations (the same applies to the boundary value problems of fractional differential equations). Moreover, the Caputo derivative for a constant is zero while the Riemann-Liouville fractional derivative of a constant is nonzero. For more details, see [13].
For the forthcoming analysis, we need the following assumptions:
(A1)let  be measurable with respect to
be measurable with respect to  for each
for each  , u.s.c. with respect to
, u.s.c. with respect to  for a.e.
for a.e.  , and for each fixed
, and for each fixed  the set
the set  is nonempty,
is nonempty,
(A2)for each  there exists a function
there exists a function  such that
such that  for each
for each  with
with  , and
, and

where  depends on
depends on  For example, for
For example, for  we have
we have  and hence
and hence  If
If  then
then  is not finite.
is not finite.
A function  is a solution of the problem (1.2) if there exists a function
is a solution of the problem (1.2) if there exists a function  such that
such that  a.e. on
a.e. on  and
and

which, in terms of Green's function  , can be expressed as
, can be expressed as

where

Here, we remark that the Green's function  for
for  takes the form (see [22])
takes the form (see [22])

Now we state the following lemmas which are necessary to establish the main result of the paper.
Lemma 2.5 (Bohnenblust-Karlin [36]).
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  , which is bounded, closed, and convex. Suppose that
, which is bounded, closed, and convex. Suppose that  is u.s.c. with closed, convex values such that
is u.s.c. with closed, convex values such that  and
and  is compact. Then G has a fixed point.
is compact. Then G has a fixed point.
Lemma 2.6 ([37]).
Let  be a compact real interval. Let
be a compact real interval. Let  be a multivalued map satisfying
be a multivalued map satisfying  and let
and let  be linear continuous from
be linear continuous from  then the operator
then the operator  is a closed graph operator in
is a closed graph operator in 
3. Main Result
Theorem 3.1.
Suppose that the assumptions  and
and  are satisfied, and
are satisfied, and

Then the antiperiodic problem (1.2) has at least one solution on 
Proof.
To transform the problem (1.2) into a fixed point problem, we define a multivalued map  as
as

Now we prove that  satisfies all the assumptions of Lemma 2.6, and thus
satisfies all the assumptions of Lemma 2.6, and thus  has a fixed point which is a solution of the problem (1.2). As a first step, we show that
has a fixed point which is a solution of the problem (1.2). As a first step, we show that  is convex for each
is convex for each  For that, let
For that, let  Then there exist
Then there exist  such that for each
such that for each  we have
we have

Let  Then, for each
Then, for each  we have
we have

Since  is convex (
is convex ( has convex values), therefore it follows that
has convex values), therefore it follows that 
In order to show that  is closed for each
is closed for each  let
let  be such that
be such that  in
in  Then
Then  and there exists a
and there exists a  such that
such that

As  has compact values, we pass onto a subsequence to obtain that
has compact values, we pass onto a subsequence to obtain that  converges to
converges to  in
in  Thus,
Thus,  and
and

Hence 
Next we show that there exists a positive number  such that
such that  where
where  Clearly
Clearly  is a bounded closed convex set in
is a bounded closed convex set in  for each positive constant
for each positive constant  If it is not true, then for each positive number
If it is not true, then for each positive number  , there exists a function
, there exists a function  with
with  and
and

On the other hand, in view of  , we have
, we have

where we have used the fact that

Dividing both sides of (3.8) by  and taking the lower limit as
and taking the lower limit as  , we find that
, we find that  which contradicts (3.1). Hence there exists a positive number
which contradicts (3.1). Hence there exists a positive number  such that
such that 
Now we show that  is equicontinuous. Let
is equicontinuous. Let  with
with  Let
Let  and
and  then there exists
then there exists  such that for each
such that for each  we have
we have

Using (3.8), we obtain

Obviously the right-hand side of the above inequality tends to zero independently of  as
as  Thus,
Thus,  is equicontinuous.
is equicontinuous.
As  satisfies the above assumptions, therefore it follows by Ascoli-Arzela theorem that
satisfies the above assumptions, therefore it follows by Ascoli-Arzela theorem that  is a compact multivalued map.
is a compact multivalued map.
Finally, we show that  has a closed graph. Let
has a closed graph. Let  and
and  We will show that
We will show that  By the relation
By the relation  we mean that there exists
we mean that there exists  such that for each
such that for each 

Thus we need to show that there exists  such that for each
such that for each 

Let us consider the continuous linear operator  so that
so that

Observe that

Thus, it follows by Lemma 2.6 that  is a closed graph operator. Further, we have
is a closed graph operator. Further, we have  Since
Since  therefore, Lemma 2.6 yields
therefore, Lemma 2.6 yields

Hence, we conclude that  is a compact multivalued map, u.s.c. with convex closed values. Thus, all the assumptions of Lemma 2.6 are satisfied and so by the conclusion of Lemma 2.6,
is a compact multivalued map, u.s.c. with convex closed values. Thus, all the assumptions of Lemma 2.6 are satisfied and so by the conclusion of Lemma 2.6,  has a fixed point
has a fixed point  which is a solution of the problem (1.2).
which is a solution of the problem (1.2).
Remark 3.2.
If we take  where
where  is a continuous function, then our results correspond to a single-valued problem (a new result).
is a continuous function, then our results correspond to a single-valued problem (a new result).
Applications
As an application of Theorem 3.1, we discuss two cases in relation to the nonlinearity  in (1.2), namely,
in (1.2), namely,  has (a) sublinear growth in its second variable (b) linear growth in its second variable (state variable). In case of sublinear growth, there exist functions
has (a) sublinear growth in its second variable (b) linear growth in its second variable (state variable). In case of sublinear growth, there exist functions  such that
such that  for each
for each  In this case,
In this case,  For the linear growth, the nonlinearity
For the linear growth, the nonlinearity  satisfies the relation
satisfies the relation  for each
for each  In this case
In this case  and the condition (3.1) modifies to
and the condition (3.1) modifies to  In both the cases, the antiperiodic problem (1.2) has at least one solution on
In both the cases, the antiperiodic problem (1.2) has at least one solution on 
Examples
-
(a)
We consider
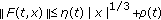 and
and 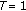 in (1.2). Here,
in (1.2). Here, 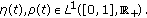 Clearly
Clearly 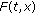 satisfies the assumptions of Theorem 3.1 with
satisfies the assumptions of Theorem 3.1 with  (condition (3.1). Thus, by the conclusion of Theorem 3.1, the antiperiodic problem (1.2) has at least one solution on
(condition (3.1). Thus, by the conclusion of Theorem 3.1, the antiperiodic problem (1.2) has at least one solution on 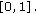
-
(b)
As a second example, let
 be such that
be such that  and
and 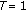 in (1.2). In this case, (3.1) takes the form
in (1.2). In this case, (3.1) takes the form 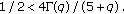 As all the assumptions of Theorem 3.1 are satisfied, the antiperiodic problem (1.2) has at least one solution on
As all the assumptions of Theorem 3.1 are satisfied, the antiperiodic problem (1.2) has at least one solution on 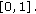
References
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Ahmad B, Sivasundaram S: Existence and uniqueness results for nonlinear boundary value problems of fractional differential equations with separated boundary conditions. to appear in Dynamic Systems and Applications
Ahmad B, Nieto JJ: Existence results for a coupled system of nonlinear functional differential equation with three-point boundary value problem. preprint
Daftardar-Gejji V, Bhalekar S: Boundary value problems for multi-term fractional differential equations. Journal of Mathematical Analysis and Applications 2008, 345(2):754–765. 10.1016/j.jmaa.2008.04.065
Erjaee GH, Momani S: Phase synchronization in fractional differential chaotic systems. Physics Letters A 2008, 372(14):2350–2354. 10.1016/j.physleta.2007.11.065
Gafiychuk V, Datsko B, Meleshko V: Mathematical modeling of time fractional reaction-diffusion systems. Journal of Computational and Applied Mathematics 2008, 220(1–2):215–225. 10.1016/j.cam.2007.08.011
Ibrahim RW, Darus M: Subordination and superordination for univalent solutions for fractional differential equations. Journal of Mathematical Analysis and Applications 2008, 345(2):871–879. 10.1016/j.jmaa.2008.05.017
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science, Amsterdam, The Netherlands; 2006:xvi+523.
Ladaci S, Loiseau JJ, Charef A: Fractional order adaptive high-gain controllers for a class of linear systems. Communications in Nonlinear Science and Numerical Simulation 2008, 13(4):707–714. 10.1016/j.cnsns.2006.06.009
Lazarević MP: Finite time stability analysis of
 fractional control of robotic time-delay systems. Mechanics Research Communications 2006, 33(2):269–279. 10.1016/j.mechrescom.2005.08.010
fractional control of robotic time-delay systems. Mechanics Research Communications 2006, 33(2):269–279. 10.1016/j.mechrescom.2005.08.010Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Rida SZ, El-Sherbiny HM, Arafa AAM: On the solution of the fractional nonlinear Schrödinger equation. Physics Letters A 2008, 372(5):553–558. 10.1016/j.physleta.2007.06.071
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon, Switzerland; 1993:xxxvi+976.
Zhang S: Existences of solutions for a boundary value problem of fractional order. Acta Mathematica Scientia 2006, 26(2):220–228. 10.1016/S0252-9602(06)60044-1
Ahmad B, Nieto JJ: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(10):3291–3298. 10.1016/j.na.2007.09.018
Ahmad B, Nieto JJ: Existence of solutions for anti-periodic boundary value problems involving fractional differential equations via Leray-Schauder degree. preprint
Chen Y, Nieto JJ, O'Regan D: Anti-periodic solutions for fully nonlinear first-order differential equations. Mathematical and Computer Modelling 2007, 46(9–10):1183–1190. 10.1016/j.mcm.2006.12.006
Franco D, Nieto JJ, O'Regan D: Anti-periodic boundary value problem for nonlinear first order ordinary differential equations. Mathematical Inequalities & Applications 2003, 6(3):477–485.
Franco D, Nieto JJ, O'Regan D: Existence of solutions for first order ordinary differential equations with nonlinear boundary conditions. Applied Mathematics and Computation 2004, 153(3):793–802. 10.1016/S0096-3003(03)00678-7
Liu B: An anti-periodic LaSalle oscillation theorem for a class of functional differential equations. Journal of Computational and Applied Mathematics 2009, 223(2):1081–1086. 10.1016/j.cam.2008.03.040
Luo Z, Shen J, Nieto JJ: Antiperiodic boundary value problem for first-order impulsive ordinary differential equations. Computers & Mathematics with Applications 2005, 49(2–3):253–261. 10.1016/j.camwa.2004.08.010
Wang K, Li Y: A note on existence of (anti-)periodic and heteroclinic solutions for a class of second-order odes. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(4):1711–1724. 10.1016/j.na.2008.02.054
Abbasbandy S, Nieto JJ, Alavi M: Tuning of reachable set in one dimensional fuzzy differential inclusions. Chaos, Solitons & Fractals 2005, 26(5):1337–1341. 10.1016/j.chaos.2005.03.018
Chang Y-K, Li W-T, Nieto JJ: Controllability of evolution differential inclusions in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(2):623–632. 10.1016/j.na.2006.06.018
Frigon M: Systems of first order differential inclusions with maximal monotone terms. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(9):2064–2077. 10.1016/j.na.2006.03.002
Nieto JJ, Rodríguez-López R: Euler polygonal method for metric dynamical systems. Information Sciences 2007, 177(20):4256–4270. 10.1016/j.ins.2007.05.002
Smirnov GV: Introduction to the Theory of Differential Inclusions, Graduate Studies in Mathematics. Volume 41. American Mathematical Society, Providence, RI, USA; 2002:xvi+226.
Chang Y-K, Nieto JJ: Existence of solutions for impulsive neutral integrodi-differential inclusions with nonlocal initial conditions via fractional operators. Numerical Functional Analysis and Optimization 2009, 30(3–4):227–244. 10.1080/01630560902841146
Chang Y-K, Nieto JJ, Li W-S: On impulsive hyperbolic differential inclusions with nonlocal initial conditions. Journal of Optimization Theory and Applications 2009, 140(3):431–442. 10.1007/s10957-008-9468-1
Henderson J, Ouahab A: Fractional functional differential inclusions with finite delay. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(5):2091–2105. 10.1016/j.na.2008.02.111
Li W-S, Chang Y-K, Nieto JJ: Existence results for impulsive neutral evolution differential inclusions with state-dependent delay. Mathematical and Computer Modelling 2009, 49(9–10):1920–1927. 10.1016/j.mcm.2008.12.010
Ouahab A: Some results for fractional boundary value problem of differential inclusions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(11):3877–3896. 10.1016/j.na.2007.10.021
Chang Y-K, Nieto JJ: Some new existence results for fractional differential inclusions with boundary conditions. Mathematical and Computer Modelling 2009, 49(3–4):605–609. 10.1016/j.mcm.2008.03.014
Deimling K: Multivalued Differential Equations, de Gruyter Series in Nonlinear Analysis and Applications. Volume 1. Walter de Gruyter, Berlin, Germany; 1992:xii+260.
Hu S, Papageorgiou N: Handbook of Multivalued Analysis, Theory Mathematics and Its Applications. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997.
Bohnenblust HF, Karlin S: On a theorem of Ville. In Contributions to the Theory of Games. Vol. I, Annals of Mathematics Studies, no. 24. Princeton University Press, Princeton, NJ, USA; 1950:155–160.
Lasota A, Opial Z: An application of the Kakutani-Ky Fan theorem in the theory of ordinary differential equations. Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques 1965, 13: 781–786.
Acknowledgments
The authors are grateful to the referees for their valuable suggestions that led to the improvement of the original manuscript. The research of V. Otero-Espinar has been partially supported by Ministerio de Educacion y Ciencia and FEDER, Project MTM2007-61724, and by Xunta de Galicia and FEDER, Project PGIDIT06PXIB207023PR.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmad, B., Otero-Espinar, V. Existence of Solutions for Fractional Differential Inclusions with Antiperiodic Boundary Conditions. Bound Value Probl 2009, 625347 (2009). https://doi.org/10.1155/2009/625347
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/625347
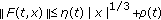 and
and 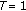 in (1.2). Here,
in (1.2). Here, 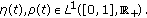 Clearly
Clearly 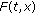 satisfies the assumptions of Theorem 3.1 with
satisfies the assumptions of Theorem 3.1 with  (condition (3.1). Thus, by the conclusion of Theorem 3.1, the antiperiodic problem (1.2) has at least one solution on
(condition (3.1). Thus, by the conclusion of Theorem 3.1, the antiperiodic problem (1.2) has at least one solution on 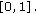
 be such that
be such that  and
and 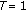 in (1.2). In this case, (3.1) takes the form
in (1.2). In this case, (3.1) takes the form 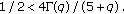 As all the assumptions of Theorem 3.1 are satisfied, the antiperiodic problem (1.2) has at least one solution on
As all the assumptions of Theorem 3.1 are satisfied, the antiperiodic problem (1.2) has at least one solution on 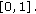
 fractional control of robotic time-delay systems. Mechanics Research Communications 2006, 33(2):269–279. 10.1016/j.mechrescom.2005.08.010
fractional control of robotic time-delay systems. Mechanics Research Communications 2006, 33(2):269–279. 10.1016/j.mechrescom.2005.08.010