- Research Article
- Open access
- Published:
Existence and Location Results for Fully Nonlinear Boundary Value Problem of n th-Order Nonlinear System
Boundary Value Problems volume 2009, Article number: 791548 (2009)
Abstract
By appropriate bounding function pair and modified functions, using the theory of differential inequalities, this paper presents the existence and location criteria of solutions for the system of general n th-order differential equations with nonlinear boundary conditions. We give an example showing that the results are sharp. Our results extend many existing results.
1. Introduction
In this paper, we are concerned with the following boundary value problem (BVP) for an  th-order nonlinear system:
th-order nonlinear system:

where 




Boundary value problems for ordinary differential equations play a very important role in both theory and applications. They are used to describe a large number of physical, biological, and chemical phenomena. There have been many accomplishments on the study of the existence of solutions for BVPs of nonlinear differential equations using the theory of differential inequalities (cf. [1–31]). Although the method has been particularly fruitful for low-order ordinary differential equations (cf. [3–8, 14, 18, 31, 32]), Kelley [33] and Klaasen [3] did obtain early applications to higher-order ODEs. For more information, we refer the readers to [2, 3, 9, 10, 12–16, 19–21, 26, 28, 33–35] and the references therein. For the case of differential systems, the results are few (cf. [2, 4–6, 8, 11, 29–32]). On the other hand, there are many papers, see [17, 18, 22, 23, 25, 36–39] and the references therein, concerning the existence of solutions for BVPs by using other approaches (e.g., the shooting method, many kinds of fixed-point theorems, many kinds of degree theories, etc.). However, there are very few results on the study of the existence of solutions for the general nonlinear system with the general nonlinear boundary conditions. To fill the gap, we will investigate BVP (1.1).
The aim of this paper is to generalize or complement the existing results. In order to do so, as a sequel of [28, 29], following the thoughts and methods of Fabry and Habets [1], the authors considered the nonlinear BVP (1.1) for differential equation and even the more general BVP (4.1) with the full nonlinear boundary conditions and obtained some results [40–43]. In this paper we consider the nonlinear BVP (1.1) for differential systems and even the more general BVP (4.1) with the full nonlinear boundary conditions. To the best of our knowledge, the general cases of BVP (1.1) and BVP (4.1) have not been studied in the available reference materials. By appropriate bounding function pair and modified functions, using the theory of differential inequalities, we establish some sufficient conditions which guarantee the existence of at least one solution for these BVPs. We give an example showing that our results are sharp.
A novel feature of our work is that we present a new definition of bounding function pair for BVP. It is well known that bounding function pair (i.e., upper-lower solutions in many references) is very important to study the existence of solutions for BVPs. Because of the complexity of the vector case (cf. [2, chapters 2 and 7]), how to give an appropriate definition of bounding function pair for the full nonlinear BVP of differential system is the difficulty in our work.
The method of this paper, which may be called simultaneous modification, is distinctive. It is not only modifying the nonlinear function in the original equations, but also transforming the original nonlinear boundary conditions into some new boundary conditions which are easy to discuss. Thus, we get the new BVP which will be discussed in the first place, then the judgement of the existence of solutions for the original BVP will be attained naturally. This technique dealing with the nonlinear problem is simpler and clearer compared with the method of shooting.
Throughout the paper, the comparison between the two vectors will be viewed as the same comparisons according to their components, and the operations between the two vectors will be viewed as the same operations according to their components.
The rest of this paper is organized as follows. In Section 2, we first give two basic definitions, that is, bounding function pair and the Nagumo condition, and then we study the modified boundary value problem of BVP (1.1), that is, BVP (2.17). Following the preparative theorem in Section 2, in Section 3, we state and prove the main result, that is, the sufficient criterion of the existence of solutions for BVP (1.1). In Section 4, a more general boundary value problem (4.1) is investigated. Moreover in Section 5, an example is illustrated to show that our results are sharp. Finally, in Section 6, some remarks are given.
2. Preparative Theorem
2.1. Basic Concepts
We first define a function

where  Moreover, if
Moreover, if

then, we define

Definition 2.1.
Assume that  . The pair of vector-valued functions
. The pair of vector-valued functions  is called a bounding function pair (or simply, a bounding pair) of BVP(1.1) in case that for some positive constant
is called a bounding function pair (or simply, a bounding pair) of BVP(1.1) in case that for some positive constant  depending on
depending on  , and for all
, and for all 
(i)
-
(ii)
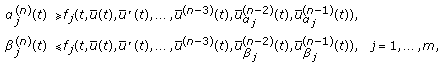 (24)
(24)
where

-
(iii)
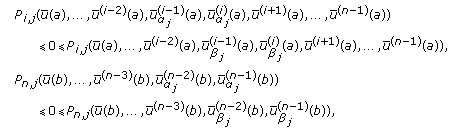 (26)
(26)
where  , and
, and

Definition 2.2.
A continuous function  is said to satisfy the Nagumo condition with respect to variable
is said to satisfy the Nagumo condition with respect to variable  on the set
on the set

in case there exist functions  , such that
, such that

2.2. The Modified Problem
Assume that there are two vector-valued functions  satisfying
satisfying

We define function  which components are
which components are

where  , and
, and 
 is a positive constant such that
is a positive constant such that


in which  .
.  is continuous, bounded, and
is continuous, bounded, and

Such function  is easy to obtain, for example, let
is easy to obtain, for example, let

In addition, we define

Then, we consider the following modified problem:

2.3. Preparative Theorem
Lemma 2.3.
Assume that
(A1)BVP (1.1) has a bounding pair  on the interval
on the interval  by Definition 2.1;
by Definition 2.1;
(A2)the function  in BVP (1.1) satisfies the Nagumo condition with respect to
in BVP (1.1) satisfies the Nagumo condition with respect to  by Definition 2.2.
by Definition 2.2.
Then, BVP (2.17) has a solution  such that
such that

where  is defined in
is defined in  .
.
The following three propositions will lead to the proof of Lemma 2.3.
Proposition 2.4.
The modified BVP (2.17) has a solution  .
.
Proof.
Noticing that the functions  and
and  (
( ) are bounded, this proposition immediately follows from the Schauder fixed-point theorem. The details here are omitted.
) are bounded, this proposition immediately follows from the Schauder fixed-point theorem. The details here are omitted.
Proposition 2.5.
Every solution  of the modified BVP (2.17) satisfies
of the modified BVP (2.17) satisfies

Proof.
First, we show that

If  is not true, then there exist some
is not true, then there exist some  and
and  such that
such that

Then,  by the boundary conditions of BVP (2.17). Thus,
by the boundary conditions of BVP (2.17). Thus,


However, on the other hand, from the definition of  and that
and that  is a solution of (2.17), we have
is a solution of (2.17), we have

This contradicts (2.23). Hence,

A similar proof shows that

Summing up, (2.20) is true. From (2.20), the function  is increasing in
is increasing in  . Noticing
. Noticing

we know that  A similar proof shows
A similar proof shows  Using the same argument, it follows that
Using the same argument, it follows that  Thus, the proof of Proposition 2.5 is completed.
Thus, the proof of Proposition 2.5 is completed.
Proposition 2.6.
Every solution  of the modified BVP (2.17) satisfies
of the modified BVP (2.17) satisfies

Proof.
Suppose that there exist some  and
and  such that
such that

Without loss of generality, we assume that  There exists
There exists  such that
such that

Hence, there exists some subinterval  such that
such that

From condition (A2),

On the other hand, from (2.13) we know that

This inequality contradicts the above one and Proposition 2.6 holds.
The proof of Lemma 2.3 is now a simple consequence of Propositions 2.4, 2.5, and 2.6.
3. Main Theorem
Now, the main result of this paper is given in the following theorem.
Theorem 3.1.
Let conditions (A1) and (A2) in Lemma 2.3 hold and assume that
(A3)the functions  are decreasing in
are decreasing in  while
while  are increasing in
are increasing in  .
.
Then, BVP (1.1) has a solution  such that
such that

where  is defined in
is defined in  .
.
Proof.
From Lemma 2.3 and the definition of  , the solution
, the solution  of the modified BVP (2.17) satisfies (1.1). Obviously, if it is proved that
of the modified BVP (2.17) satisfies (1.1). Obviously, if it is proved that  satisfies the boundary conditions of (1.1) under condition (A3), we may conclude that
satisfies the boundary conditions of (1.1) under condition (A3), we may conclude that  is just the solution of BVP (1.1).
is just the solution of BVP (1.1).
First, we prove that

Case 1.
Suppose that

Then

Thus,

Case 2.
Suppose that there exist some  and some
and some  such that
such that

Then,

Hence,

From Proposition 2.5,

From Proposition 2.6,

When  , Proposition 2.5 implies
, Proposition 2.5 implies

When  , formula (3.7) implies
, formula (3.7) implies

Recalling that  ,
,  , we get
, we get  . Thus,
. Thus,

It follows from formulas (3.7)–(3.13) and condition (A3) that, for  ,
,

It is easy to see that the last inequality contradicts (iii) of Definition 2.1. Therefore, Case 2 is not true.
Case 3.
Suppose that there exist some  and some
and some  such that
such that

Then,

Hence,

Similar to the argument of Case 2, we have

Obviously, the last inequality contradicts (iii) of Definition 2.1. Therefore, this case cannot hold. Summing up, (3.2) holds.
A similar proof shows that

Consequently, the proof is completed.
Remark 3.2.
From (iii) of Definition 2.1 and (A3) of Theorem 3.1, it is easy to see that the functions  should be increasing in
should be increasing in 
4. A Generalized Problem
Now, we consider the following boundary value problem with more generalized boundary conditions:

where  and
and  are continuous m-dimensional vector-valued functions.
are continuous m-dimensional vector-valued functions.
Similar to Definition 2.1, we give the following.
Definition 4.1.
Assume  , The pair of vector-valued functions
, The pair of vector-valued functions  is called a bounding function pair of BVP (4.1) in case that
is called a bounding function pair of BVP (4.1) in case that
(i)same as (i) of Definition 2.1;
(ii)same as (ii) of Definition 2.1;
(iii)′

where 
For BVP (4.1), we have the following existence theorem.
Theorem 4.2.
Assume that
(A1)′BVP (4.1) has a bounding function pair  in the interval I by Definition 4.1;
in the interval I by Definition 4.1;
(A2)′the function  in BVP (4.1) satisfies the Nagumo condition with respect to
in BVP (4.1) satisfies the Nagumo condition with respect to  by Definition 2.2;
by Definition 2.2;
(A3)′the functions 
 are decreasing in
are decreasing in  while
while 
 are increasing in
are increasing in  .
.
Then, BVP (4.1) has a solution  such that
such that

where  is defined in
is defined in  .
.
Proof.
Consider the modified problem

The modified function  is defined as BVP (2.17), and
is defined as BVP (2.17), and

where 

Using the same argument as the proof of Lemma 2.3, it follows from conditions (A1)′ and (A2)′ that BVP (4.4) has a solution  satisfying the two inequalities in the conclusions of Lemma 2.3. Furthermore, in an analogous way to the proof of Theorem 3.1, it follows that the solution
satisfying the two inequalities in the conclusions of Lemma 2.3. Furthermore, in an analogous way to the proof of Theorem 3.1, it follows that the solution  of BVP(4.4) is just a solution of BVP (4.1). Consequently, the proof of Theorem 4.2 is completed. The details of the proof will be omitted.
of BVP(4.4) is just a solution of BVP (4.1). Consequently, the proof of Theorem 4.2 is completed. The details of the proof will be omitted.
Remark 4.3.
From (iii)′ of Definition 4.1 and (A3)′ of Theorem 4.2, it is easy to see that the functions  should be increasing in
should be increasing in 
5. An Example
In this section, we present an example by making use of Theorems 3.1 and 4.2. With the example, we try to illustrate the applicability of our results and techniques and show that a bounding pair according to Definitions 2.1 or 4.1 can exist naturally.
Example 5.1.
Consider the following 4th-order nonlinear system:

together with the following boundary conditions:

where  , and
, and  is a constant.
is a constant.
Let

Then, for the case of  and the case of
and the case of  , by direct calculation, it is easy to check that
, by direct calculation, it is easy to check that  is a bounding pair of BVP (5.1) and all assumptions of Theorems 3.1 and 4.2 are fulfilled, respectively. Hence, for any of the two cases, BVP (5.1) has at least one solution
is a bounding pair of BVP (5.1) and all assumptions of Theorems 3.1 and 4.2 are fulfilled, respectively. Hence, for any of the two cases, BVP (5.1) has at least one solution  satisfying
satisfying

for each 
6. Remarks
-
(1)
If the directions of the signs of inequalities in condition (iii) of Definition 2.1 are all changed to the opposite, and conditions (i), (ii) of Definition 2.1 hold, then we denote the revised definition by Definition 2.1. We obtain the following theorem similar to Theorem 3.1.
Theorem 6.1.
Assume that
(A1)′′BVP (1.1) has a bounding function pair  by Definition 6.1;
by Definition 6.1;
(A2)same as (A2) of Theorem 3.1;
(A3)′′the monotony of  is opposite to that of (A3) .
is opposite to that of (A3) .
Then, the conclusion of Theorem3.1 still holds.
In fact, if we replace  by
by  in Theorem 3.1, then, it follows from Theorem 3.1 that Theorem 6.1 is true. We may make the analogous argument for BVP (4.1).
in Theorem 3.1, then, it follows from Theorem 3.1 that Theorem 6.1 is true. We may make the analogous argument for BVP (4.1).
-
(2)
The essentiality of the modified function is to modify a general nonlinear continuous function to a continuous bounded function. It was appearing in different forms in references. In this paper, we give out one concise form.
-
(3)
The definitions of scalar bounding functions are a good many. In this paper, the definitions in vector cases given are new and can be regarded as a kind of improvement and generalization. Of course, the conditions of the definitions may be changed by the actual need. For example, we take Definition 2.1 to discuss the following.
If  in
in  of condition (ii) are changed to
of condition (ii) are changed to  , respectively, we still may assure that those results hold.
, respectively, we still may assure that those results hold.
If both  and
and  in
in  of condition (ii) are modified to
of condition (ii) are modified to  , we may simplify the depiction and the proof. But, the modified condition becomes stronger.
, we may simplify the depiction and the proof. But, the modified condition becomes stronger.
It should be pointed out that condition (ii) may be weakened as

However, when proving Proposition 2.5, we should add one condition " are all decreasing in
are all decreasing in  ". Thus, (*) implies condition (ii) of Definition 2.1. Consequently, condition (ii) about
". Thus, (*) implies condition (ii) of Definition 2.1. Consequently, condition (ii) about  seems weaker, but in fact, the whole requirement becomes stronger in some sense.
seems weaker, but in fact, the whole requirement becomes stronger in some sense.
We also may discuss condition (iii) of Definition 2.1 in a similar way.
-
(4)
The Nagumo condition in this paper ensures that the integral inequality (2.13) is true and essentially ensures that the derivative functions of solutions of the considered problems are bounded. Indeed, in some references, the integral equality
 (61)
(61)
is straightly substituted by inequality (2.13). Moreover, we exhibit some new forms of the integral inequality (see [29]).
-
(5)
From Theorems 3.1, 4.2, and the above remarks, we include or improve the results in [1–43], since our system and boundary conditions are fully nonlinear. Obviously, the results in all the references are not available to our example.
-
(6)
Last but not least, it should be pointed out that although this paper presents the existence and location criteria of solutions for BVPs, the premise is that the bounding function pair is assumed to be existing. It is well known how to get a precise bounding function pair for a given BVP is a very difficult job in the theory of upper-lower solutions and remains unsolved.
References
Fabry Ch, Habets P: Upper and lower solutions for second-order boundary value problems with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(10):985–1007. 10.1016/0362-546X(86)90084-2
Chang KW, Howes FA: Nonlinear Singular Perturbation Phenomena: Theory and Applications, Applied Mathematical Sciences. Volume 56. Springer, New York, NY, USA; 1984:viii+180.
Klaasen GA: Differential inequalities and existence theorems for second and third order boundary value problems. Journal of Differential Equations 1971, 10(3):529–537. 10.1016/0022-0396(71)90010-6
Howes FA: Differential inequalities and applications to nonlinear singular perturbation problems. Journal of Differential Equations 1976, 20(1):133–149. 10.1016/0022-0396(76)90100-5
Kelley WG: A geometric method of studying two point boundary value problems for second order systems. The Rocky Mountain Journal of Mathematics 1977, 7(2):251–263. 10.1216/RMJ-1977-7-2-251
Kelley WG: Second order systems with nonlinear boundary conditions. Proceedings of the American Mathematical Society 1977, 62(2):287–292. 10.1090/S0002-9939-1977-0445051-3
Erbe LH: Existence of solutions to boundary value problems for second order differential equations. Nonlinear Analysis: Theory, Methods & Applications 1982, 6(11):1155–1162. 10.1016/0362-546X(82)90027-X
O'Donnell MA: Boundary and corner layer behavior in singularly perturbed semilinear systems of boundary value problems. SIAM Journal on Mathematical Analysis 1984, 15(2):317–332. 10.1137/0515025
Cabada A: The method of lower and upper solutions for th-order periodic boundary value problems. Journal of Applied Mathematics and Stochastic Analysis 1994, 7(1):33–47. 10.1155/S1048953394000043
Cabada A: The method of lower and upper solutions for second, third, fourth, and higher order boundary value problems. Journal of Mathematical Analysis and Applications 1994, 185(2):302–320. 10.1006/jmaa.1994.1250
Butuzov VF, Nefedov NN, Schneider KR: Singularly perturbed boundary value problems for systems of Tichonov's type in case of exchange of stabilities. Journal of Differential Equations 1999, 159(2):427–446. 10.1006/jdeq.1999.3670
Cabada A, Grossinho MdoR, Minhós F: On the solvability of some discontinuous third order nonlinear differential equations with two point boundary conditions. Journal of Mathematical Analysis and Applications 2003, 285(1):174–190. 10.1016/S0022-247X(03)00388-3
Cabada A, Liz E: Boundary value problems for higher order ordinary differential equations with impulses. Nonlinear Analysis: Theory, Methods & Applications 1998, 32(6):775–786. 10.1016/S0362-546X(97)00523-3
Cabada A, Minhós FM: Fully nonlinear fourth-order equations with functional boundary conditions. Journal of Mathematical Analysis and Applications 2008, 340(1):239–251. 10.1016/j.jmaa.2007.08.026
Du Z, Ge W, Lin X: Existence of solutions for a class of third-order nonlinear boundary value problems. Journal of Mathematical Analysis and Applications 2004, 294(1):104–112. 10.1016/j.jmaa.2004.02.001
Ehme J, Eloe PW, Henderson J: Existence of solutions for
 th order nonlinear generalized Sturm-Liouville boundary value problems. Mathematical Inequalities & Applications 2001, 4(2):247–255.
th order nonlinear generalized Sturm-Liouville boundary value problems. Mathematical Inequalities & Applications 2001, 4(2):247–255.Ehme J: Uniqueness and existence for perturbed focal boundary value problems. Applied Mathematics Letters 2005, 18(8):875–879. 10.1016/j.aml.2004.10.004
Ehme J, Lanz A: Uniqueness and existence for bounded boundary value problems. Journal of Mathematical Analysis and Applications 2006, 319(2):725–731. 10.1016/j.jmaa.2005.06.029
Sadyrbaev F: Nonlinear fourth-order two-point boundary value problems. The Rocky Mountain Journal of Mathematics 1995, 25(2):757–781. 10.1216/rmjm/1181072248
Franco D, O'Regan D, Perán J: Fourth-order problems with nonlinear boundary conditions. Journal of Computational and Applied Mathematics 2005, 174(2):315–327. 10.1016/j.cam.2004.04.013
Guo D: Extremal solutions for th-order impulsive integro-differential equations on the half-line in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2006, 65(3):677–696. 10.1016/j.na.2005.09.032
Li Y: Existence and uniqueness for higher order periodic boundary value problems under spectral separation conditions. Journal of Mathematical Analysis and Applications 2006, 322(2):530–539. 10.1016/j.jmaa.2005.08.054
Liu Y, Yang P, Ge W: Solutions of two-point BVPs at resonance for higher order impulsive differential equations. Nonlinear Analysis: Theory, Methods & Applications 2005, 60(5):887–923. 10.1016/j.na.2004.09.054
El-Shahed M: Positive solutions of boundary value problems for th order ordinary differential equations. Electronic Journal of Qualitative Theory of Differential Equations 2008, (1):1–9.
Pang C, Dong W, Wei Z: Green's function and positive solutions of th order -point boundary value problem. Applied Mathematics and Computation 2006, 182(2):1231–1239. 10.1016/j.amc.2006.05.010
Šeda V, Nieto JJ, Gera M: Periodic boundary value problems for nonlinear higher order ordinary differential equations. Applied Mathematics and Computation 1992, 48(1):71–82. 10.1016/0096-3003(92)90019-W
Yang B: Estimates of positive solutions for higher order right focal boundary value problem. Communications in Mathematical Analysis 2008, 4(1):1–9.
Wang GW, Sun L: Existence of solutions of nonlinear two-point boundary value problems for fourth-order differential equations. Journal of Xuzhou Normal University 2001, 19(2):1–5.
Wang GW, Zhou MR, Sun L: Existence of solutions of two-point boundary value problems for the systems of
 th-order differential equations. Journal of Nanjing University. Mathematical Biquarterly 2002, 19(1):68–79.
th-order differential equations. Journal of Nanjing University. Mathematical Biquarterly 2002, 19(1):68–79.Yang X: Existence of positive solutions for
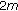 -order nonlinear differential systems. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(1–2):77–95. 10.1016/j.na.2004.11.013
-order nonlinear differential systems. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(1–2):77–95. 10.1016/j.na.2004.11.013Yang X: The method of lower and upper solutions for systems of boundary value problems. Applied Mathematics and Computation 2003, 144(1):169–172. 10.1016/S0096-3003(02)00400-9
Lasota A, Yorke JA: Existence of solutions of two-point boundary value problems for nonlinear systems. Journal of Differential Equations 1972, 11: 509–518. 10.1016/0022-0396(72)90063-0
Kelley WG: Some existence theorems for
 th-order boundary value problems. Journal of Differential Equations 1975, 18(1):158–169. 10.1016/0022-0396(75)90086-8
th-order boundary value problems. Journal of Differential Equations 1975, 18(1):158–169. 10.1016/0022-0396(75)90086-8Ehme J, Eloe PW, Henderson J: Upper and lower solution methods for fully nonlinear boundary value problems. Journal of Differential Equations 2002, 180(1):51–64. 10.1006/jdeq.2001.4056
Du Z, Ge W, Zhou M: Singular perturbations for third-order nonlinear multi-point boundary value problem. Journal of Differential Equations 2005, 218(1):69–90. 10.1016/j.jde.2005.01.005
Agarwal RP, Kiguradze I: Two-point boundary value problems for higher-order linear differential equations with strong singularities. Boundary Value Problems 2006, 2006:-32.
Agarwal RP, Wong PJY: Existence of solutions for singular boundary problems for higher order differential equations. Rendiconti del Seminario Matematico e Fisico di Milano 1995, 65(1):249–264. 10.1007/BF02925259
Kiguradze I: On periodic solutions of
 th order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2000, 40(1–8):309–321.
th order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2000, 40(1–8):309–321.Kiguradze IT, Kusano T: On periodic solutions of higher-order nonautonomous ordinary differential equations. Differential Equations 1999, 35(1):70–77.
Wang G, Zhou M, Sun L: Bounding functions methods for fully nonlinear boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(4):696–705. 10.1016/j.na.2005.06.027
Wang G, Zhou M, Sun L: Differential inequalities method to
 th-order boundary value problems. Journal of Inequalities and Applications 2006, 2006:-12.
th-order boundary value problems. Journal of Inequalities and Applications 2006, 2006:-12.Wang G, Zhou M, Sun L: Existence of solutions of boundary value problem for 3rd order nonlinear system. Applied Mathematics and Computation 2007, 189(2):1131–1138. 10.1016/j.amc.2006.12.003
Wang G, Zhou M, Sun L: Fourth-order problems with fully nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2007, 325(1):130–140. 10.1016/j.jmaa.2006.01.059
Acknowledgments
The authors would like to express their gratitude to the reviewers for their careful reading of the manuscript and for their very helpful comments. This paper is supported by Science Research Innovation Project for Graduates of Jiangsu Province (CX07B-029Z), Natural Science Foundation of XZNU (08XLB03) and Qing Lan Project of XZNU.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, L., Zhou, M. & Wang, G. Existence and Location Results for Fully Nonlinear Boundary Value Problem of n th-Order Nonlinear System. Bound Value Probl 2009, 791548 (2009). https://doi.org/10.1155/2009/791548
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/791548
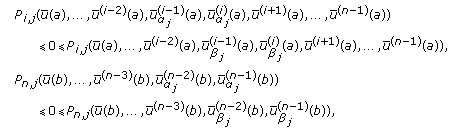

 th order nonlinear generalized Sturm-Liouville boundary value problems. Mathematical Inequalities & Applications 2001, 4(2):247–255.
th order nonlinear generalized Sturm-Liouville boundary value problems. Mathematical Inequalities & Applications 2001, 4(2):247–255. th-order differential equations. Journal of Nanjing University. Mathematical Biquarterly 2002, 19(1):68–79.
th-order differential equations. Journal of Nanjing University. Mathematical Biquarterly 2002, 19(1):68–79. -order nonlinear differential systems. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(1–2):77–95. 10.1016/j.na.2004.11.013
-order nonlinear differential systems. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(1–2):77–95. 10.1016/j.na.2004.11.013 th-order boundary value problems. Journal of Differential Equations 1975, 18(1):158–169. 10.1016/0022-0396(75)90086-8
th-order boundary value problems. Journal of Differential Equations 1975, 18(1):158–169. 10.1016/0022-0396(75)90086-8 th order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2000, 40(1–8):309–321.
th order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2000, 40(1–8):309–321. th-order boundary value problems. Journal of Inequalities and Applications 2006, 2006:-12.
th-order boundary value problems. Journal of Inequalities and Applications 2006, 2006:-12.