- Research Article
- Open access
- Published:
Limit Properties of Solutions of Singular Second-Order Differential Equations
Boundary Value Problems volume 2009, Article number: 905769 (2009)
Abstract
We discuss the properties of the differential equation  , a.e. on
, a.e. on  , where
, where  , and
, and  satisfies the
satisfies the  -Carathéodory conditions on
-Carathéodory conditions on  for some
for some  . A full description of the asymptotic behavior for
. A full description of the asymptotic behavior for  of functions
of functions  satisfying the equation a.e. on
satisfying the equation a.e. on  is given. We also describe the structure of boundary conditions which are necessary and sufficient for
is given. We also describe the structure of boundary conditions which are necessary and sufficient for  to be at least in
to be at least in  . As an application of the theory, new existence and/or uniqueness results for solutions of periodic boundary value problems are shown.
. As an application of the theory, new existence and/or uniqueness results for solutions of periodic boundary value problems are shown.
1. Motivation
In this paper, we study the analytical properties of the differential equation

where  ,
,  , and the function
, and the function  is defined for a.e.
is defined for a.e.  and for all
and for all  . The above equation is singular at
. The above equation is singular at  because of the first term in the right-hand side, which is in general unbounded for
because of the first term in the right-hand side, which is in general unbounded for  . In this paper, we will also alow the function
. In this paper, we will also alow the function  to be unbounded or bounded but discontinuous for certain values of the time variable
to be unbounded or bounded but discontinuous for certain values of the time variable  . This form of
. This form of  is motivated by a variety of initial and boundary value problems known from applications and having nonlinear, discontinuous forcing terms, such as electronic devices which are often driven by square waves or more complicated discontinuous inputs. Typically, such problems are modelled by differential equations where
is motivated by a variety of initial and boundary value problems known from applications and having nonlinear, discontinuous forcing terms, such as electronic devices which are often driven by square waves or more complicated discontinuous inputs. Typically, such problems are modelled by differential equations where  has jump discontinuities at a discrete set of points in
has jump discontinuities at a discrete set of points in  , compare [1].
, compare [1].
This study serves as a first step toward analysis of more involved nonlinearities, where typically,  has singular points also in
has singular points also in  and
and  . Many applications, compare [2–12], showing these structural difficulties are our main motivation to develop a framework on existence and uniqueness of solutions, their smoothness properties, and the structure of boundary conditions necessary for
. Many applications, compare [2–12], showing these structural difficulties are our main motivation to develop a framework on existence and uniqueness of solutions, their smoothness properties, and the structure of boundary conditions necessary for  to have at least continuous first derivative on
to have at least continuous first derivative on  . Moreover, using new techniques presented in this paper, we would like to extend results from [13, 14] (based on ideas presented in [15]) where problems of the above form but with appropriately smooth data function
. Moreover, using new techniques presented in this paper, we would like to extend results from [13, 14] (based on ideas presented in [15]) where problems of the above form but with appropriately smooth data function have been discussed.
have been discussed.
Here, we aim at the generalization of the existence and uniqueness assertions derived in those papers for the case of smooth  . We are especially interested in studying the limit properties of
. We are especially interested in studying the limit properties of  for
for  and the structure of boundary conditions which are necessary and sufficient for
and the structure of boundary conditions which are necessary and sufficient for  to be at least in
to be at least in  .
.
To clarify the aims of this paper and to show that it is necessary to develop a new technique to treat the nonstandard equation given above, let us consider a model problem which we designed using the structure of the boundary value problem describing a membrane arising in the theory of shallow membrane caps and studied in [10]; see also [6, 9],

subject to boundary conditions

where  Note that (1.2) can be written in the form
Note that (1.2) can be written in the form

which is of form (1.1) with

Function  is not defined for
is not defined for  and for
and for  if
if  . We now briefly discuss a simplified linear model of (1.4),
. We now briefly discuss a simplified linear model of (1.4),

where  and
and  . Clearly, this means that
. Clearly, this means that  .
.
The question which we now pose is the role of the boundary conditions (1.3), more precisely, are these boundary conditions necessary and sufficient for the solution  of (1.6) to be unique and at least continuously differentiable,
of (1.6) to be unique and at least continuously differentiable,  ? To answer this question, we can use techniques developed in the classical framework dealing with boundary value problems, exhibiting a singularity of the first and second kind; see [15, 16], respectively. However, in these papers, the analytical properties of the solution
? To answer this question, we can use techniques developed in the classical framework dealing with boundary value problems, exhibiting a singularity of the first and second kind; see [15, 16], respectively. However, in these papers, the analytical properties of the solution  are derived for nonhomogeneous terms being at least continuous. Clearly, we need to rewrite problem (1.6) first and obtain its new form stated as,
are derived for nonhomogeneous terms being at least continuous. Clearly, we need to rewrite problem (1.6) first and obtain its new form stated as,

which suggest to introduce a new variable,  . In a general situation, especially for the nonlinear case, it is not straightforward to provide such a transformation, however. We now introduce
. In a general situation, especially for the nonlinear case, it is not straightforward to provide such a transformation, however. We now introduce  and immediately obtain the following system of ordinary differential equations:
and immediately obtain the following system of ordinary differential equations:

where  or equivalently,
or equivalently,

where  . According to [16], the latter system of equations has a continuous solution if and only if the regularity condition
. According to [16], the latter system of equations has a continuous solution if and only if the regularity condition  holds. This results in
holds. This results in

compare conditions (1.3). Note that the Euler transformation,  which is usually used to transform (1.6) to the first-order form would have resulted in the following system:
which is usually used to transform (1.6) to the first-order form would have resulted in the following system:

Here,  may become unbounded for
may become unbounded for  , the condition
, the condition  , or equivalently
, or equivalently  is not the correct condition for the solution
is not the correct condition for the solution  to be continuous on
to be continuous on 
From the above remarks, we draw the conclusion that a new approach is necessary to study the analytical properties of (1.1).
2. Introduction
The following notation will be used throughout the paper. Let  be an interval. Then, we denote by
be an interval. Then, we denote by  the set of functions which are (Lebesgue) integrable on
the set of functions which are (Lebesgue) integrable on  . The corresponding norm is
. The corresponding norm is  . Let
. Let  . By
. By  , we denote the set of functions whose
, we denote the set of functions whose  th powers of modulus are integrable on
th powers of modulus are integrable on  with the corresponding norm given by
with the corresponding norm given by  .
.
Moreover, let us by  and
and  denote the sets of functions being continuous on
denote the sets of functions being continuous on  and having continuous first derivatives on
and having continuous first derivatives on  , respectively. The norm on
, respectively. The norm on  is defined as
is defined as  .
.
Finally, we denote by  and
and  the sets of functions which are absolutely continuous on
the sets of functions which are absolutely continuous on  and which have absolutely continuous first derivatives on
and which have absolutely continuous first derivatives on  , respectively. Analogously,
, respectively. Analogously,  and
and  are the sets of functions being absolutely continuous on each compact subinterval
are the sets of functions being absolutely continuous on each compact subinterval  and having absolutely continuous first derivatives on each compact subinterval
and having absolutely continuous first derivatives on each compact subinterval  , respectively.
, respectively.
As already said in the previous section, we investigate differential equations of the form

where  . For the subsequent analysis we assume that
. For the subsequent analysis we assume that

specified in the following definition.
Definition 2.1.
Let  . A function
. A function  satisfies the
satisfies the -Carathéodory conditions on the set
-Carathéodory conditions on the set  if
if
(i)  is measurable for all
is measurable for all  ,
,
(ii)  is continuous for a.e.
is continuous for a.e.  ,
,
(iii) for each compact set  there exists a function
there exists a function  such that
such that  for a.e.
for a.e.  and all
and all  .
.
We will provide a full description of the asymptotical behavior for  of functions
of functions  satisfying (2.1) a.e. on
satisfying (2.1) a.e. on  . Such functions
. Such functions  will be called solutions of (2.1) if they additionally satisfy the smoothness requirement
will be called solutions of (2.1) if they additionally satisfy the smoothness requirement  ; see next definition.
; see next definition.
Definition 2.2.
A function  is called a solution of (2.1) if
is called a solution of (2.1) if  and satisfies
and satisfies

In Section 3, we consider linear problems and characterize the structure of boundary conditions necessary for the solution to be at least continuous on  . These results are modified for nonlinear problems in Section 4. In Section 5, by applying the theory developed in Section 4, we provide new existence and/or uniqueness results for solutions of singular boundary value problems (2.1) with periodic boundary conditions.
. These results are modified for nonlinear problems in Section 4. In Section 5, by applying the theory developed in Section 4, we provide new existence and/or uniqueness results for solutions of singular boundary value problems (2.1) with periodic boundary conditions.
3. Linear Singular Equation
First, we consider the linear equation,  ,
,

where  and
and  .
.
As a first step in the analysis of (3.1), we derive the necessary auxiliary estimates used in the discussion of the solution behavior. For  , let us denote by
, let us denote by

Assume that  . Then
. Then

Now, let  ,
,  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  . For
. For  , we choose
, we choose  , and we have
, and we have  and
and  .
.
First, let  . Then
. Then  ,
,  , and
, and

Now, let  . Then
. Then  ,
,  , and
, and

Hence, for  ,
,  ,
,

Consequently, (3.3), (3.6), and the Hölder inequality yield,  ,
,

Therefore


which means that  . We now use the properties of
. We now use the properties of  to represent all functions
to represent all functions  satisfying (3.1) a.e. on
satisfying (3.1) a.e. on  . Remember that such function
. Remember that such function  does not need to be a solution of (3.1) in the sense of Definition 2.2.
does not need to be a solution of (3.1) in the sense of Definition 2.2.
Lemma 3.1.
Let  ,
,  , and let
, and let  be given by (3.2).
be given by (3.2).
(i) If  , then
, then

is the set of all functions  satisfying (3.1) a.e. on
satisfying (3.1) a.e. on  .
.
(ii) If  , then
, then

is the set of all functions  satisfying (3.1) a.e. on
satisfying (3.1) a.e. on  .
.
Proof.
Let  . Note that (3.1) is linear and regular on
. Note that (3.1) is linear and regular on  . Since the functions
. Since the functions  and
and  are linearly independent solutions of the homogeneous equation
are linearly independent solutions of the homogeneous equation  on
on  , the general solution of the homogeneous problem is
, the general solution of the homogeneous problem is

Moreover, the function  is a particular solution of (3.1) on
is a particular solution of (3.1) on  . Therefore, the first statement follows. Analogous argument yields the second assertion.
. Therefore, the first statement follows. Analogous argument yields the second assertion.
We stress that by (3.8), the particular solution  of (3.1) belongs to
of (3.1) belongs to  . For
. For  , we can see from (3.9) that it is useful to find other solution representations which are equivalent to (3.10) and (3.11), but use
, we can see from (3.9) that it is useful to find other solution representations which are equivalent to (3.10) and (3.11), but use  instead of
instead of  , if
, if  .
.
Lemma 3.2.
Let  and let
and let  be given by (3.2).
be given by (3.2).
(i) If  , then
, then

is the set of all functions  satisfying (3.1) a.e. on
satisfying (3.1) a.e. on  .
.
(ii) If  , then
, then

is the set of all functions  satisfying (3.1) a.e. on
satisfying (3.1) a.e. on  .
.
Proof.
Let us fix  and define
and define

In order to prove (i) we have to show that  for
for  , where
, where  . This follows immediately from (3.9), since
. This follows immediately from (3.9), since

and hence we can define  as follows:
as follows:

For  we have
we have

which completes the proof.
Again, by (3.9), the particular solution,

of (3.1) for  satisfies
satisfies  . Main results for the linear singular equation (3.1) are now formulated in the following theorems.
. Main results for the linear singular equation (3.1) are now formulated in the following theorems.
Theorem 3.3.
Let  and let
and let  satisfy equation (3.1) a.e. on
satisfy equation (3.1) a.e. on  . Then
. Then

Moreover,  can be extended to the whole interval
can be extended to the whole interval  in such a way that
in such a way that  .
.
Proof.
Let a function  be given. Then, by (3.10), there exist two constants
be given. Then, by (3.10), there exist two constants  such that for
such that for  ,
,

Using (3.8), we conclude

For  and
and  , we have
, we have  . Furthermore, for a.e.
. Furthermore, for a.e.  ,
,

By the Hölder inequality and (3.6) it follows that

where

Therefore  , and consequently
, and consequently  .
.
It is clear from the above theorem, that  given by (3.21) is a solution of (3.1) for
given by (3.21) is a solution of (3.1) for  . Let us now consider the associated boundary value problem,
. Let us now consider the associated boundary value problem,


where  are real matrices, and
are real matrices, and  is an arbitrary vector. Then the following result follows immediately from Theorem 3.3.
is an arbitrary vector. Then the following result follows immediately from Theorem 3.3.
Theorem 3.4.
Let  ,
,  . Then for any
. Then for any  and any
and any  there exists a unique solution
there exists a unique solution  of the boundary value problem (3.26a) and (3.26b) if and only if the following matrix,
of the boundary value problem (3.26a) and (3.26b) if and only if the following matrix,

is nonsingular.
Proof.
Let  be a solution of (3.1). Then
be a solution of (3.1). Then  satisfies (3.21), and the result follows immediately by substituting the values,
satisfies (3.21), and the result follows immediately by substituting the values,

into the boundary conditions (3.26b).
Theorem 3.5.
Let  and let a function
and let a function  satisfy equation (3.1) a.e. on
satisfy equation (3.1) a.e. on  . For
. For  , only one of the following properties holds:
, only one of the following properties holds:
(i)  ,
,  ,
,
(ii)  ,
,  .
.
For  ,
,  satisfies only one of the following properties:
satisfies only one of the following properties:
(i)  ,
,  ,
,
(ii)  ,
,  .
.
In particular,  can be extended to the whole interval
can be extended to the whole interval  with
with  if and only if
if and only if  .
.
Proof.
Let  , and let
, and let  be given. Then, by (3.13), there exist two constants
be given. Then, by (3.13), there exist two constants  such that
such that

Hence

Let  , then it follows from (3.9)
, then it follows from (3.9)  . Also, by (3.29),
. Also, by (3.29),  . Let
. Let  . Then (3.9), (3.29), and (3.30) imply that
. Then (3.9), (3.29), and (3.30) imply that

Let  . Then, by (3.14), for any
. Then, by (3.14), for any  ,
,


If  , then
, then  by (3.9), and it follows from (3.32) that
by (3.9), and it follows from (3.32) that  . Let
. Let  . Then we deduce from (3.9), (3.32), and (3.33) that
. Then we deduce from (3.9), (3.32), and (3.33) that

Let  . Then on
. Then on  ,
,  satisfies (3.29) and (3.30), with
satisfies (3.29) and (3.30), with  . If
. If  , then, by (3.9),
, then, by (3.9),  and
and  . Let
. Let  . Then
. Then

In particular, for  ,
,  can be extended to
can be extended to  in such a way that
in such a way that  if and only if
if and only if  . Then, the associated boundary conditions read
. Then, the associated boundary conditions read  and
and  . Finally, for a.e.
. Finally, for a.e.  ,
,

and by the Hölder inequality, (3.3), and (3.25),

Therefore  , and consequently
, and consequently  .
.
Again, it is clear that  given by (3.29) for
given by (3.29) for  and
and  , and
, and  given by (3.32) for
given by (3.32) for  is a solution of (3.1), and
is a solution of (3.1), and  if and only if
if and only if  . Let us now consider the boundary value problem
. Let us now consider the boundary value problem


where  are real constants. Then the following result follows immediately from Theorem 3.5.
are real constants. Then the following result follows immediately from Theorem 3.5.
Theorem 3.6.
Let  ,
,  . Then for any
. Then for any  and any
and any  there exists a unique solution
there exists a unique solution  of the boundary value problem (3.38a) and (3.38b) if and only if
of the boundary value problem (3.38a) and (3.38b) if and only if  .
.
Proof.
Let  be a solution of (3.1). Then
be a solution of (3.1). Then  satisfies (3.29) for
satisfies (3.29) for  and
and  , and (3.32) for
, and (3.32) for  . We first note that, by (3.9), for all
. We first note that, by (3.9), for all  ,
,

Therefore,  in both, (3.29) and (3.32), and the result now follows by substituting the values,
in both, (3.29) and (3.32), and the result now follows by substituting the values,

into the boundary conditions (3.38b).
To illustrate the solution behaviour, described by Theorems 3.3 and 3.5, we have carried out a series of numerical calculations on a MATLAB software package bvpsuite designed to solve boundary value problems in ordinary differential equations. The solver is based on a collocation method with Gaussian collocation points. A short description of the code can be found in [17]. This software has already been used for a variety of singular boundary value problems relevant for applications; see, for example, [18].
The equations being dealt with are of the form

subject to initial or boundary conditions specified in the following graphs. All solutions were computed on the unit interval  .
.
Finally, we expect  , and therefore we solve (3.41) subject to the terminal conditions
, and therefore we solve (3.41) subject to the terminal conditions  . See Figures 1, 2, and 3.
. See Figures 1, 2, and 3.
Illustrating Theorem 3. 3: solutions of differential equation (3.41) with  , subject to boundary conditions
, subject to boundary conditions  . See graph legend for the values of
. See graph legend for the values of  and
and  . According to Theorem 3.3 it holds that
. According to Theorem 3.3 it holds that  for each choice of
for each choice of  and
and  .
.
Illustrating Theorem 3. 5 for  : solutions of differential equation (3.41) with
: solutions of differential equation (3.41) with  , subject to boundary conditions
, subject to boundary conditions  . See graph legend for the values of
. See graph legend for the values of  and
and  . According to Theorem 3.5 a solution
. According to Theorem 3.5 a solution  satisfies
satisfies  or
or  or
or  in dependence of values
in dependence of values  and
and  . In order to precisely recover a solution satisfying
. In order to precisely recover a solution satisfying  , the respective simulation was carried out as an initial value problem with
, the respective simulation was carried out as an initial value problem with  and
and  .
.
Illustrating Theorem 3. 5 for  : solutions of differential equation (3.41) with
: solutions of differential equation (3.41) with  , subject to boundary conditions
, subject to boundary conditions  . See graph legend for the values of
. See graph legend for the values of  and
and  . Here,
. Here,  , and
, and  , or
, or  ,
,  .
.
4. Limit Properties of Functions Satisfying Nonlinear Singular Equations
In this section we assume that the function  satisfying differential equation (2.1) a.e. on
satisfying differential equation (2.1) a.e. on  is given. The first derivative of such a function does not need to be continuous at
is given. The first derivative of such a function does not need to be continuous at  and hence, due to the lack of smoothness,
and hence, due to the lack of smoothness,  does not need to be a solution of (2.1) in the sense of Definition 2.2. In the following two theorems, we discuss the limit properties of
does not need to be a solution of (2.1) in the sense of Definition 2.2. In the following two theorems, we discuss the limit properties of  for
for  .
.
Theorem 4.1.
Let us assume that (2.2) holds. Let  and let
and let  satisfy equation (2.1) a.e. on
satisfy equation (2.1) a.e. on  . Finally, let us assume that that
. Finally, let us assume that that

Then

and  can be extended on
can be extended on  in such a way that
in such a way that  .
.
Proof.
Let  for a.e.
for a.e.  . By (2.2), there exists a function
. By (2.2), there exists a function  such that
such that  for a.e.
for a.e.  . Therefore,
. Therefore,  . Since the equality
. Since the equality  holds a.e. on
holds a.e. on  , the result follows immediately due to Theorem 3.3.
, the result follows immediately due to Theorem 3.3.
Theorem 4.2.
Let us assume that condition (2.2) holds. Let  and let
and let  satisfy equation (2.1) a.e. on
satisfy equation (2.1) a.e. on  . Let us also assume that (4.1) holds. Then
. Let us also assume that (4.1) holds. Then

and  can be extended on
can be extended on  in such a way that
in such a way that  .
.
Proof.
Let  be as in the proof of Theorem 4.1. According to Theorem 3.5 and (4.1),
be as in the proof of Theorem 4.1. According to Theorem 3.5 and (4.1),  satisfies (4.3) both for
satisfies (4.3) both for  and
and  .
.
5. Applications
Results derived in Theorems 4.1 and 4.2 constitute a useful tool when investigating the solvability of nonlinear singular equations subject to different types of boundary conditions. In this section, we utilize Theorem 4.1 to show the existence of solutions for periodic problems. The rest of this section is devoted to the numerical simulation of such problems.
Periodic Problem
We deal with a problem of the following form:


Definition 5.1.
A function  is called a solution of the boundary value problem (5.1a) and (5.1b), if
is called a solution of the boundary value problem (5.1a) and (5.1b), if  satisfies equation (5.1a) for a.e.
satisfies equation (5.1a) for a.e.  and the periodic boundary conditions (5.1b).
and the periodic boundary conditions (5.1b).
Conditions (5.1b) can be written in the form (3.26b) with  ,
,  , and
, and  . Then, matrix (3.27) has the form
. Then, matrix (3.27) has the form

and we see that it is singular. Consequently, the assumption of Theorem 3.4 is not satisfied, and the linear periodic problem (3.26b) subject to (5.1b) is not uniquely solvable. However this is not true for nonliner periodic problems. In particular, Theorem 5.6 gives a characterization of a class of nonlinear periodic problems (5.1a) and (5.1b) which have only one solution. We begin the investigation of problem (5.1a) and (5.1b) with a uniqueness result.
Theorem 5.2 (uniqueness).
Let  and let us assume that condition (2.2) holds. Further, assume that for each compact set
and let us assume that condition (2.2) holds. Further, assume that for each compact set  there exists a nonnegative function
there exists a nonnegative function  such that
such that

for a.e.  and all
and all  . Then problem (5.1a) and (5.1b) has at most one solution.
. Then problem (5.1a) and (5.1b) has at most one solution.
Proof.
Let  and
and  be different solutions of problem (5.1a) and (5.1b). Since
be different solutions of problem (5.1a) and (5.1b). Since  , there exists a compact set
, there exists a compact set  such that
such that  for
for  . Let us define the difference function
. Let us define the difference function  for
for  . Then
. Then

First, we prove that there exists an interval  such that
such that

We consider two cases.
Case 1.
Assume that  and
and  have an intersection point, that is, there exists
have an intersection point, that is, there exists  such that
such that  . Since
. Since  and
and  are different, there exists
are different, there exists  ,
,  , such that
, such that  .
.
-
(i)
Let
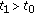 . We can assume that
. We can assume that 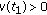 . (Otherwise we choose
. (Otherwise we choose 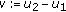 .) Then we can find
.) Then we can find  satisfying
satisfying  for
for 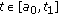 and
and  . Let
. Let 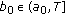 be the first zero of
be the first zero of 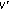 . Then, if we set
. Then, if we set  , we see that
, we see that 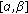 satisfies (5.5). Let
satisfies (5.5). Let 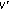 have no zeros on
have no zeros on 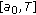 . Then
. Then 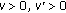 on
on 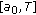 , and, due to (5.4),
, and, due to (5.4),  . Since
. Since  , we can find
, we can find 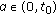 and
and 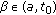 such that
such that 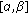 satisfies (5.5).
satisfies (5.5). -
(ii)
Let
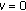 on
on 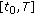 . By (5.4),
. By (5.4), 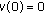 ,
, 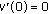 and
and 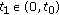 . We may again assume that
. We may again assume that 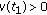 . It is possible to find
. It is possible to find 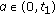 such that
such that 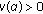 ,
,  ,
, 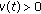 on
on 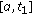 . Since
. Since  ,
, 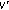 has at least one zero in
has at least one zero in 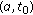 . If
. If  is the first zero of
is the first zero of  , then
, then 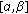 satisfies (5.5).
satisfies (5.5).
Case 2.
Assume that  and
and  have no common point, that is,
have no common point, that is,  on
on  . We may assume that
. We may assume that  on
on  . By (5.4), there exists a point
. By (5.4), there exists a point  satisfying
satisfying  .
.
-
(i)
Let
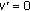 on
on 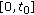 . Then, by (5.1a) and (5.3),
. Then, by (5.1a) and (5.3), 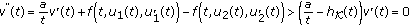 (5.6)
(5.6)
for a.e.  , which is a contradiction to
, which is a contradiction to  on
on  .
.
-
(ii)
Let
 for some
for some  . If
. If  , then we can find an interval
, then we can find an interval  satisfying (5.5). If
satisfying (5.5). If 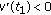 and
and 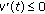 on
on  , then
, then  and, by (5.4),
and, by (5.4), 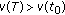 ,
, 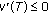 . Hence, there exists an interval
. Hence, there exists an interval 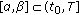 satisfying (5.5).
satisfying (5.5).
To summarize, we have shown that in both, the case of intersecting solutions  and
and  and the case of separated
and the case of separated  and
and  , there exists an interval
, there exists an interval  satisfying (5.5).
satisfying (5.5).
Now, by (5.1a), (5.3), and (5.5), we obtain

Denote by  . Then
. Then  , and
, and  for a.e.
for a.e.  . Consequently,
. Consequently,

Integrating the last inequality in  , we obtain
, we obtain

which contradicts  . Consequently, we have shown that
. Consequently, we have shown that  , and the result follows.
, and the result follows.
In the following theorem we formulate sufficient conditions for the existence of at least one solution of problem (5.1a) and (5.1b) with  . In the proof of this theorem, we work also with auxiliary two-point boundary conditions:
. In the proof of this theorem, we work also with auxiliary two-point boundary conditions:

Under the assumptions of Theorem 4.1 any solution of (5.1a) satisfies  Therefore, we can investigate (5.1a) subject to the auxiliary conditions (5.10) instead of the equivalent original problem (5.1a) and (5.1b). This change of the problem setting is useful for obtaining of a priori estimates necessary for the application of the Fredholm-type existence theorem (Lemma 5.5) during the proof.
Therefore, we can investigate (5.1a) subject to the auxiliary conditions (5.10) instead of the equivalent original problem (5.1a) and (5.1b). This change of the problem setting is useful for obtaining of a priori estimates necessary for the application of the Fredholm-type existence theorem (Lemma 5.5) during the proof.
Theorem 5.3 (existence).
Let  and let (2.2) hold. Further, assume that there exist
and let (2.2) hold. Further, assume that there exist  ,
,  ,
,  , and
, and  such that
such that  ,
,

for a.e.  ,
,

for a.e.  and all
and all  , where
, where

Then problem (5.1a) and (5.1b) has a solution  such that
such that

Proof.
Step 1 (existence of auxiliary solutions  ).
).
By (5.13), there exists  such that
such that

For  , let
, let

Motivated by [19], we choose  ,
,  , and, for a.e.
, and, for a.e.  , all
, all  , and
, and  , we define the following functions:
, we define the following functions:



Due to (5.11),

for a.e.  . It can be shown that
. It can be shown that  and
and  which satisfy the
which satisfy the  -Carathéodory conditions on
-Carathéodory conditions on  are nondecreasing in their second argument and
are nondecreasing in their second argument and  a.e. on
a.e. on  ; see [19]. Therefore,
; see [19]. Therefore,  also satisfies the
also satisfies the  -Carathéodory conditions on
-Carathéodory conditions on  , and there exists a function
, and there exists a function  such that
such that  for a.e.
for a.e.  and all
and all  .
.
We now investigate the auxiliary problem

Since the homogeneous problem  , has only the trivial solution, we conclude by the Fredholm-type Existence Theorem (see Lemma 5.5) that there exists a solution
, has only the trivial solution, we conclude by the Fredholm-type Existence Theorem (see Lemma 5.5) that there exists a solution  of problem (5.21).
of problem (5.21).
Step 2 (estimates of  ).
).
We now show that

Let us define  for
for  and assume
and assume

By (5.21), we can assume that  . Since
. Since  , we can find
, we can find  such that
such that

Then, by (5.19), (5.20), and (5.21), we have

for a.e.  . Hence,
. Hence,

which contradicts (5.23), and thus  on
on  . The inequality
. The inequality  on
on  can be proved in a very similar way.
can be proved in a very similar way.
Step 3 (estimates of  ).
).
We now show that

By (5.19) and (5.22) we have  for a.e.
for a.e.  , and so, due to (5.17) and (5.21), we have for a.e.
, and so, due to (5.17) and (5.21), we have for a.e.  ,
,

Denote  . If
. If  , then
, then  .
.
Case 1.
Let  . Then there exists
. Then there exists  such that
such that  on
on  ,
,  . By (5.12), (5.22), (5.28), and
. By (5.12), (5.22), (5.28), and  , it follows for a.e.
, it follows for a.e.  ,
,

Consequently,

where  is given by (5.15). Therefore
is given by (5.15). Therefore  .
.
Case 2.
Let  . Then there exists
. Then there exists  such that
such that  on
on  ,
,  . By (5.12), (5.13), (5.22), (5.28), and
. By (5.12), (5.13), (5.22), (5.28), and  , we obtain for a.e.
, we obtain for a.e. 

Consequently,

Hence, according to (5.15), we again have  .
.
Step 4 (convergence of  ).
).
Consider the sequence  of solutions of problems (5.21),
of solutions of problems (5.21),  ,
,  . It has been shown in Steps 2 and 3 that (5.22) and (5.27) hold, which means that the sequences
. It has been shown in Steps 2 and 3 that (5.22) and (5.27) hold, which means that the sequences  and
and  are bounded in
are bounded in  . Therefore
. Therefore  is equicontinuous on
is equicontinuous on  . According to (5.17), (5.19), and (5.21), we obtain for
. According to (5.17), (5.19), and (5.21), we obtain for  ,
,

Let us now choose an arbitrary compact subinterval  . Then there exists
. Then there exists  such that
such that  for each
for each  . By (5.33), the sequence
. By (5.33), the sequence  is equicontinuous on
is equicontinuous on  . Therefore, we can find a subsequence
. Therefore, we can find a subsequence  such that
such that  converges uniformly on
converges uniformly on  , and
, and  converges uniformly on
converges uniformly on  . By the diagonalization theorem; see [11], we can find a subsequence
. By the diagonalization theorem; see [11], we can find a subsequence  such that there exists
such that there exists  with
with

Therefore  and
and  . For
. For  in (5.33), Lebesgue's dominated convergence theorem yields
in (5.33), Lebesgue's dominated convergence theorem yields

Consequently,  satisfies equation (5.1a) a.e. on
satisfies equation (5.1a) a.e. on  . Moreover, due to (5.22) and (5.27), we have
. Moreover, due to (5.22) and (5.27), we have

Hence (4.1) is satisfied. Applying Theorem 4.1, we conclude that  and
and  . Therefore
. Therefore  satisfies the periodic conditions on
satisfies the periodic conditions on  . Thus
. Thus  is a solution of problem (5.1a) and (5.1b) and
is a solution of problem (5.1a) and (5.1b) and  on
on  .
.
Example 5.4.
Let  ,
,  ,
,  ,
,  for some
for some  , and
, and  . Moreover, let
. Moreover, let  be nonnegative, and let
be nonnegative, and let  be bounded on
be bounded on  . Then in Theorem 5.3 the following class of functions
. Then in Theorem 5.3 the following class of functions  is covered:
is covered:

for a.e.  and all
and all  , provided
, provided  if
if  and
and  if
if  . In particular, for
. In particular, for  ,
, 

or

In order to show the existence of solutions to the periodic boundary value problem (5.1a) and (5.1b), the Fredholm-type Existence Theorem is used, see for example, in [20, Theorem  ], [11, Theorem
], [11, Theorem  ] or [21, page 25]. For convenience, we provide its simple formulation suitable for our purpose below.
] or [21, page 25]. For convenience, we provide its simple formulation suitable for our purpose below.
Lemma 5.5 (Fredholm-type existence theorem).
Let  satisfy (2.2), let matrices
satisfy (2.2), let matrices  , vector
, vector  be given, and let
be given, and let  . Let us denote by
. Let us denote by  , and assume that the linear homogeneous boundary value problem
, and assume that the linear homogeneous boundary value problem

has only the trivial solution. Moreover, let us assume that there exists a function  such that
such that

Then the problem

has a solution  .
.
If we combine Theorems 5.2 and 5.3, we obtain conditions sufficient for the solution of (5.1a) and (5.1b) to be unique.
Theorem 5.6 (existence and uniqueness).
Let all assumptions of Theorems 5.2 and 5.3 hold. Then problem (5.1a) and (5.1b) has a unique solution  . Moreover
. Moreover  satisfies (5.14).
satisfies (5.14).
Example 5.7.
Functions satisfying assumptions of Theorem 5.6 can have the form


for  .
.
We now illustrate the above theoretical findings by means of numerical simulations. Figure 4 shows graphs of solutions of problem (5.43), (5.1a). In Figure 5 we display the error estimate for the global error of the numerical solution and the so-called residual (defect) obtained from the substitution of the numerical solution into the differential equation. Both quantities are rather small and indicate that we have found a solution to the analytical problem (5.43)-(5.1a).
Illustrating Theorem 5. 6: solutions of differential equation (5.43), subject to periodic boundary conditions (5.1a). See graph legend for the values of  .
.
We now pose that question about the values of the first derivative at the end points of the interval of integration,  and
and  . According to the theory, it holds that
. According to the theory, it holds that  . Therefore, we approximate the values of the first derivative of the numerical solution and show these values in Figure 6. One can see that indeed
. Therefore, we approximate the values of the first derivative of the numerical solution and show these values in Figure 6. One can see that indeed  . Also, to support this observation, we plotted in Figure 7 the numerical solutions obtained for the step size
. Also, to support this observation, we plotted in Figure 7 the numerical solutions obtained for the step size  tending to zero, or equivalently, grids becoming finer.
tending to zero, or equivalently, grids becoming finer.
We finally observe experimentally the order of convergence of the numerical method (collocation). Clearly, we do not expect very hight order to hold, since the analytical solution has nonsmooth higher derivatives. However, the method is convergent and, according to Table 1, we observe that its order tends to  .
.
The results of the numerical simulation for the boundary value problem (5.44)-(5.1a), can be found in Figures 8, 9, 10, and 11.
References
Lee JW, O'Regan D: Existence of solutions to some initial value, two-point, and multi-point boundary value problems with discontinuous nonlinearities. Applicable Analysis 1989, 33(1-2):57-77. 10.1080/00036818908839861
Agarwal RP, O'Regan D: Singular problems arising in circular membrane theory. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2003, 10(6):965-972.
Baxley JV: A singular nonlinear boundary value problem: membrane response of a spherical cap. SIAM Journal on Applied Mathematics 1988, 48(3):497-505. 10.1137/0148028
Baxley JV, Gersdorff GS: Singular reaction-diffusion boundary value problems. Journal of Differential Equations 1995, 115(2):441-457. 10.1006/jdeq.1995.1022
Constantin A: Sur un probleme aux limites en mecanique non lineaire. Comptes Rendus de l'Académie des Sciences. Série I 1995, 320(12):1465-1468.
Dickey RW: Rotationally symmetric solutions for shallow membrane caps. Quarterly of Applied Mathematics 1989, 47(3):571-581.
Dickey RW: The plane circular elastic surface under normal pressure. Archive for Rational Mechanics and Analysis 1967, 26(3):219-236.
Hlavacek V, Marek M, Kubicek M: Modelling of chemical reactors-X. Multiple solutions of enthalpy and mass balances for a catalytic reaction within a porous catalyst particle. Chemical Engineering Science 1968, 23(9):1083-1097. 10.1016/0009-2509(68)87093-9
Johnson KN: Circularly symmetric deformation of shallow elastic membrane caps. Quarterly of Applied Mathematics 1997, 55(3):537-550.
Rachůnková I, Koch O, Pulverer G, Weinmüller E: On a singular boundary value problem arising in the theory of shallow membrane caps. Journal of Mathematical Analysis and Applications 2007, 332(1):523-541. 10.1016/j.jmaa.2006.10.006
Rachůnková I, Staněk S, Tvrdý M: Singularities and Laplacians in boundary value problems for nonlinear ordinary differential equations. In Handbook of Differential Equations: Ordinary Differential Equations, Handbook of Differential Equations. Volume 3. Edited by: Caňada A, Drábek P, Fonda A. Elsevier, Amsterdam, The Netherlands; 2006:607-722.
Shin JY: A singular nonlinear differential equation arising in the Homann flow. Journal of Mathematical Analysis and Applications 1997, 212(2):443-451. 10.1006/jmaa.1997.5516
Weinmüller E: On the boundary value problem for systems of ordinary second-order differential equations with a singularity of the first kind. SIAM Journal on Mathematical Analysis 1984, 15(2):287-307. 10.1137/0515023
Koch O: Asymptotically correct error estimation for collocation methods applied to singular boundary value problems. Numerische Mathematik 2005, 101(1):143-164. 10.1007/s00211-005-0617-2
de Hoog FR, Weiss R: Difference methods for boundary value problems with a singularity of the first kind. SIAM Journal on Numerical Analysis 1976, 13(5):775-813. 10.1137/0713063
de Hoog FR, Weiss R: The numerical solution of boundary value problems with an essential singularity. SIAM Journal on Numerical Analysis 1979, 16(4):637-669. 10.1137/0716049
Kitzhofer G: Numerical treatment of implicit singular BVPs, Ph.D. thesis. Institute for Analysis and Scientific Computing, Vienna University of Technology, Vienna, Austria; 2005. in prepartion
Rachůnková I, Pulverer G, Weinmüller E: A unified approach to singular problems arising in the membran theory. to appear in Applications of Mathematics
Kiguradze IT, Shekhter BL: Singular boundary value problems for second-order ordinary differential equations. In Current Problems in Mathematics. Newest Results, Vol. 30 (Russian), Itogi Nauki i Tekhniki. Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, Russia; 1987:105-201. translated in Journal of Soviet Mathematics, vol. 43, no. 2, pp. 2340–2417, 1988
Lasota A: Sur les problèmes linéaires aux limites pour un système d'équations différentielles ordinaires. Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques 1962, 10: 565-570.
Vasiliev NI, Klokov JA: Foundation of the Theory of Boundary Value Problems for Ordinary Differential Equations. Zinatne, Riga, Russia; 1978.
Acknowledgments
This research was supported by the Council of Czech Goverment MSM6198959214 and by the Grant no. A100190703 of the Grant Agency of the Academy of Sciences of the Czech Republic.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rachůnková, I., Staněk, S., Weinmüller, E. et al. Limit Properties of Solutions of Singular Second-Order Differential Equations. Bound Value Probl 2009, 905769 (2009). https://doi.org/10.1155/2009/905769
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/905769



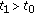 . We can assume that
. We can assume that 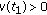 . (Otherwise we choose
. (Otherwise we choose 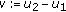 .) Then we can find
.) Then we can find  satisfying
satisfying  for
for 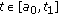 and
and  . Let
. Let 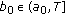 be the first zero of
be the first zero of 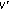 . Then, if we set
. Then, if we set  , we see that
, we see that 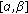 satisfies (5.5). Let
satisfies (5.5). Let 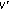 have no zeros on
have no zeros on 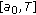 . Then
. Then 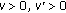 on
on 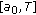 , and, due to (5.4),
, and, due to (5.4),  . Since
. Since  , we can find
, we can find 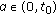 and
and 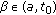 such that
such that 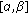 satisfies (5.5).
satisfies (5.5).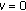 on
on 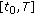 . By (5.4),
. By (5.4), 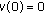 ,
, 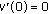 and
and 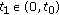 . We may again assume that
. We may again assume that 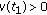 . It is possible to find
. It is possible to find 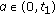 such that
such that 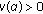 ,
,  ,
, 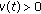 on
on 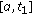 . Since
. Since  ,
, 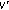 has at least one zero in
has at least one zero in 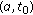 . If
. If  is the first zero of
is the first zero of  , then
, then 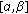 satisfies (5.5).
satisfies (5.5).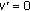 on
on 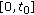 . Then, by (5.1a) and (5.3),
. Then, by (5.1a) and (5.3), 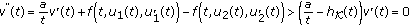
 for some
for some  . If
. If  , then we can find an interval
, then we can find an interval  satisfying (5.5). If
satisfying (5.5). If 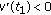 and
and 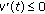 on
on  , then
, then  and, by (5.4),
and, by (5.4), 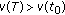 ,
, 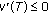 . Hence, there exists an interval
. Hence, there exists an interval 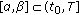 satisfying (5.5).
satisfying (5.5).

 .
.
 .
.
 in the vicinity of
in the vicinity of  (a) and
(a) and  (b). The step size is decreasing according to
(b). The step size is decreasing according to  .
.
 .
.
 .
.
 .
.
 in the vicinity of
in the vicinity of  (a) and
(a) and  (b). The step size is decreasing according to
(b). The step size is decreasing according to  .
.