- Research Article
- Open access
- Published:
A Viral Infection Model with a Nonlinear Infection Rate
Boundary Value Problems volume 2009, Article number: 958016 (2009)
Abstract
A viral infection model with a nonlinear infection rate is constructed based on empirical evidences. Qualitative analysis shows that there is a degenerate singular infection equilibrium. Furthermore, bifurcation of cusp-type with codimension two (i.e., Bogdanov-Takens bifurcation) is confirmed under appropriate conditions. As a result, the rich dynamical behaviors indicate that the model can display an Allee effect and fluctuation effect, which are important for making strategies for controlling the invasion of virus.
1. Introduction
Mathematical models can provide insights into the dynamics of viral load in vivo. A basic viral infection model [1] has been widely used for studying the dynamics of infectious agents such as hepatitis B virus (HBV), hepatitis C virus (HCV), and human immunodeficiency virus (HIV), which has the following forms:

where susceptible cells ( ) are produced at a constant rate
) are produced at a constant rate  , die at a density-dependent rate
, die at a density-dependent rate  , and become infected with a rate
, and become infected with a rate  ; infected cells (
; infected cells ( ) are produced at rate
) are produced at rate  and die at a density-dependent rate
and die at a density-dependent rate  ; free virus particles (
; free virus particles ( ) are released from infected cells at the rate
) are released from infected cells at the rate  and die at a rate
and die at a rate  . Recently, there have been many papers on virus dynamics within-host in different aspects based on the (1.1). For example, the influences of spatial structures on virus dynamics have been considered, and the existence of traveling waves is established via the geometric singular perturbation method [2]. For more literature, we list [3, 4] and references cited therein.
. Recently, there have been many papers on virus dynamics within-host in different aspects based on the (1.1). For example, the influences of spatial structures on virus dynamics have been considered, and the existence of traveling waves is established via the geometric singular perturbation method [2]. For more literature, we list [3, 4] and references cited therein.
Usually, there is a plausible assumption that the amount of free virus is simply proportional to the number of infected cells because the dynamics of the virus is substantially faster than that of the infected cells,  . Thus, the number of infected cells
. Thus, the number of infected cells  can also be considered as a measure of virus load
can also be considered as a measure of virus load  (e.g., see [5–7]). As a result, the model (1.1) is reduced to
(e.g., see [5–7]). As a result, the model (1.1) is reduced to

As for this model, it is easy to see that the basic reproduction number of virus is given by  , which describes the average number of newly infected cells generated from one infected cell at the beginning of the infectious process. Furthermore, we know that the infection-free equilibrium
, which describes the average number of newly infected cells generated from one infected cell at the beginning of the infectious process. Furthermore, we know that the infection-free equilibrium  is globally asymptotically stable if
is globally asymptotically stable if  , and so is the infection equilibrium
, and so is the infection equilibrium  if
if  .
.
Note that both infection terms in (1.1) and (1.2) are based on the mass-action principle (Perelson and Nelson [8]); that is, the infection rate per susceptible cell and per virus is a constant  . However, infection experiments of Ebert et al. [9] and McLean and Bostock [10] suggest that the infection rate of microparasitic infections is an increasing function of the parasite dose and is usually sigmoidal in shape. Thus, as Regoes et al. [11], we take the nonlinear infection rate into account by relaxing the mass-action assumption that is made in (1.2) and obtain
. However, infection experiments of Ebert et al. [9] and McLean and Bostock [10] suggest that the infection rate of microparasitic infections is an increasing function of the parasite dose and is usually sigmoidal in shape. Thus, as Regoes et al. [11], we take the nonlinear infection rate into account by relaxing the mass-action assumption that is made in (1.2) and obtain

where the infection rate per susceptible cell,  , is a sigmoidal function of the virus (parasite) concentration because the number of infected cells
, is a sigmoidal function of the virus (parasite) concentration because the number of infected cells  can also be considered as a measure of virus load (e.g., see [5–7]), which is represented in the following form:
can also be considered as a measure of virus load (e.g., see [5–7]), which is represented in the following form:

Here,  denotes the infectious dose at which
denotes the infectious dose at which  of the susceptible cells are infected,
of the susceptible cells are infected,  measures the slope of the sigmoidal curve at
measures the slope of the sigmoidal curve at  and approximates the average number of virus that enters a single host cell at the begin stage of invasion,
and approximates the average number of virus that enters a single host cell at the begin stage of invasion,  measures the infection force of the virus, and
measures the infection force of the virus, and  measures the inhibition effect from the behavioral change of the susceptible cells when their number increases or from the production of immune response which depends on the infected cells.
measures the inhibition effect from the behavioral change of the susceptible cells when their number increases or from the production of immune response which depends on the infected cells.
In fact, many investigators have introduced different functional responses into related equations for epidemiological modeling, of which we list [12–17] and references cited therein. However, a few studies have considered the influences of nonlinear infection rate on virus dynamics. When the parameter  , [18, 19] considered a viral mathematical model with the nonlinear infection rate and time delay. Furthermore, some different types of nonlinear functional responses, in particular of the form
, [18, 19] considered a viral mathematical model with the nonlinear infection rate and time delay. Furthermore, some different types of nonlinear functional responses, in particular of the form  or Holling-type functional response, were investigated in [20–23].
or Holling-type functional response, were investigated in [20–23].
Note that  in (1.4). To simplify the study, we fix the slope
in (1.4). To simplify the study, we fix the slope  in the present paper, and system (1.3) becomes
in the present paper, and system (1.3) becomes

To be concise in notations, rescale (1.5) by  . For simplicity, we still use variables
. For simplicity, we still use variables  instead of
instead of  and obtain
and obtain

where  . Note that
. Note that  is the average life time of susceptible cells and
is the average life time of susceptible cells and  is the average life-time of infected cells. Thus,
is the average life-time of infected cells. Thus,  is always valid by means of biological detection. If
is always valid by means of biological detection. If  , the virus does not kill infected cells. Therefore, the virus is non cytopathic in vivo. However, when
, the virus does not kill infected cells. Therefore, the virus is non cytopathic in vivo. However, when  , which means that the virus kills infected cells before its average life time, the virus is cytopathic in vivo.
, which means that the virus kills infected cells before its average life time, the virus is cytopathic in vivo.
The main purpose of this paper is to study the effect of the nonlinear infection rate on the dynamics of (1.6). We will perform a qualitative analysis and derive the Allee-type dynamics which result from the appearance of bistable states or saddle-node state in (1.6). The bifurcation analysis indicates that (1.6) undergoes a Bogdanov-Takens bifurcation at the degenerate singular infection equilibrium which includes a saddle-node bifurcation, a Hopf bifurcation, and a homoclinic bifurcation. Thus, the nonlinear infection rate can induce the complex dynamic behaviors in the viral infection model.
The organization of the paper is as follows. In Section 2, the qualitative analysis of system (1.6) is performed, and the stability of the equilibria is obtained. The results indicate that (1.6) can display an Allee effect. Section 3 gives the bifurcation analysis, which indicates that the dynamics of (1.6) is more complex than that of (1.1) and (1.2). Finally, a brief discussion on the direct biological implications of the results is given in Section 4.
2. Qualitative Analysis
Since we are interested in virus pathogenesis and not initial processes of infection, we assume that the initial data for the system (1.6) are such that

The objective of this section is to perform a qualitative analysis of system (1.6) and derive the Allee-type dynamics. Clearly, the solutions of system (1.6) with positive initial values are positive and bounded. Let  , and note that (1.6) has one and only one infection-free equilibrium
, and note that (1.6) has one and only one infection-free equilibrium  . Then by using the formula of a basic reproduction number for the compartmental models in van den Driessche and Watmough [24], we know that the basic reproduction number of virus of (1.6) is
. Then by using the formula of a basic reproduction number for the compartmental models in van den Driessche and Watmough [24], we know that the basic reproduction number of virus of (1.6) is

which describes the average number of newly infected cells generated from one infected cell at the beginning of the infectious process as zero. Although it is zero, we will show that the virus can still persist in host.
We start by studying the equilibria of (1.6). Obviously, the infection-free equilibrium  always exists and is a stable hyperbolic node because the corresponding characteristic equation is
always exists and is a stable hyperbolic node because the corresponding characteristic equation is  .
.
In order to find the positive (infection) equilibria, set

then we have the equation

Based on (2.4), we can obtain that
(i) there is no infection equilibria if  ;
;
(ii) there is a unique infection equilibrium  if
if  ;
;
(iii) there are two infection equilibria  and
and  if
if  .
.
Here,

Thus, the surface

is a Saddle-Node bifurcation surface, that is, on one side of the surface  system (1.6) has not any positive equilibria; on the surface
system (1.6) has not any positive equilibria; on the surface  system (1.6) has only one positive equilibrium; on the other side of the surface
system (1.6) has only one positive equilibrium; on the other side of the surface  system (1.6) has two positive equilibria. The detailed results will follow.
system (1.6) has two positive equilibria. The detailed results will follow.
Next, we determine the stability of  and
and  . The Jacobian matrix at
. The Jacobian matrix at  is
is

After some calculations, we have

Since  in this case,
in this case,  is valid. Thus,
is valid. Thus,  and the equilibrium
and the equilibrium  is a saddle.
is a saddle.
The Jacobian matrix at  is
is

By a similar argument as above, we can obtain that  . Thus, the equilibrium
. Thus, the equilibrium  is a node, or a focus, or a center.
is a node, or a focus, or a center.
For the sake of simplicity, we denote

We have the following results on the stability of  .
.
Theorem 2.1.
Suppose that equilibrium  exists; that is,
exists; that is,  . Then
. Then  is always stable if
is always stable if  . When
. When  , we have
, we have
(i)  is stable if
is stable if  ;
;
(ii)  is unstable if
is unstable if  ;
;
(iii)  is a linear center if
is a linear center if  .
.
Proof.
After some calculations, the matrix trace of  is
is

and its sign is determined by

Note that

which means that  is a monotone decreasing function of variable
is a monotone decreasing function of variable  .
.
Clearly,

Note that  implies that
implies that

Squaring (2.15) we find that

Thus,

This means that  . Thus, under the condition of
. Thus, under the condition of  and the sign of
and the sign of  ,
,  is always valid if
is always valid if  . When
. When  ,
,  if
if  ,
,  if
if  , and
, and  if
if  .
.
For (1.6), its asymptotic behavior is determined by the stability of  if it does not have a limit cycle. Next, we begin to consider the nonexistence of limit cycle in (1.6).
if it does not have a limit cycle. Next, we begin to consider the nonexistence of limit cycle in (1.6).
Note that  is a saddle and
is a saddle and  is a node, a focus, or a center. A limit cycle of (1.6) must include
is a node, a focus, or a center. A limit cycle of (1.6) must include  and does not include
and does not include  . Since the flow of (1.6) moves toward down on the line where
. Since the flow of (1.6) moves toward down on the line where  and
and  and moves towards up on the line where
and moves towards up on the line where  and
and  , it is easy to see that any potential limit cycle of (1.6) must lie in the region where
, it is easy to see that any potential limit cycle of (1.6) must lie in the region where  . Take a Dulac function
. Take a Dulac function  , and denote the right-hand sides of (1.6) by
, and denote the right-hand sides of (1.6) by  and
and  , respectively. We have
, respectively. We have

which is negative if  . Hence , we can obtain the following result.
. Hence , we can obtain the following result.
Theorem 2.2.
There is no limit cycle in (1.6) if

Note that  as long as it exists. Thus, inequality (2.19) is always valid if
as long as it exists. Thus, inequality (2.19) is always valid if  . When
. When  , using the expression of
, using the expression of  in (2.5), we have that inequality (2.19) that is equivalent to
in (2.5), we have that inequality (2.19) that is equivalent to

Indeed, since

we have (2.19) that is equivalent to

that is,

Thus,

On the other hand, squaring (2.23) we find that

which is equivalent to

The combination of (2.24) and (2.26) yields (2.20).
Furthermore,

is equivalent to  , both
, both

are equivalent to  . Consequently, we have the following.
. Consequently, we have the following.
Corollary 2.3.
There is no limit cycle in (1.6) if either of the following conditions hold:
(i)  and
and  ;
;
(ii)  and
and  .
.
When  , system (1.6) has a unique infection equilibrium
, system (1.6) has a unique infection equilibrium  . The Jacobian matrix at
. The Jacobian matrix at  is
is

The determinant of  is
is

and the trace of  is
is

Thus,  is a degenerate singular point. Since its singularity, complex dynamic behaviors may occur, which will be studied in the next section.
is a degenerate singular point. Since its singularity, complex dynamic behaviors may occur, which will be studied in the next section.
3. Bifurcation Analysis
In this section, the Bogdanov-Takens bifurcation (for short, BT bifurcation) of system (1.6) is studied when there is a unique degenerate infection equilibrium  .
.
For simplicity of computation, we introduce the new time  by
by  , rewrite
, rewrite  as
as  , and obtain
, and obtain

Note that (3.1) and (1.6) are  -equivalent; both systems have the same dynamics (only the time changes).
-equivalent; both systems have the same dynamics (only the time changes).
As the above mentioned, assume that
(H1) 
Then (3.1) admits a unique positive equilibrium  , where
, where

In order to translate the positive equilibrium  to origin, we set
to origin, we set  and obtain
and obtain

Since we are interested in codimension  bifurcation, we assume further that
bifurcation, we assume further that
(H2) 
Then, after some transformations, we have the following result.
Theorem 3.1.
The equilibrium  of (1.6) is a cusp of codimension
of (1.6) is a cusp of codimension  if (H1) and (H2) hold; that is, it is a Bogdanov-Takens singularity.
if (H1) and (H2) hold; that is, it is a Bogdanov-Takens singularity.
Proof.
Under assumptions (H1) and (H2), it is clear that the linearized matrix of (3.3)

has two zero eigenvalues. Let  . Since the parameters
. Since the parameters  satisfy the assumptions (H1) and (H2), after some algebraic calculations, (3.3) is transformed into
satisfy the assumptions (H1) and (H2), after some algebraic calculations, (3.3) is transformed into

where  ,
,  , are smooth functions in variables
, are smooth functions in variables  at least of the third order. Using an affine translation
at least of the third order. Using an affine translation  to (3.5), we obtain
to (3.5), we obtain

where  ,
,  , are smooth functions in variables
, are smooth functions in variables  at least of order three. To obtain the canonical normal forms, we perform the transformation of variables by
at least of order three. To obtain the canonical normal forms, we perform the transformation of variables by

Then, (3.6) becomes

where  ,
,  , are smooth functions in
, are smooth functions in  at least of the third order.
at least of the third order.
Obviously,

This implies that the origin of (3.3), that is,  of (1.6), is a cusp of codimension
of (1.6), is a cusp of codimension  by in [25, Theorem
by in [25, Theorem  , Section
, Section  ].
].
In the following we will investigate the approximating BT bifurcation curves. The parameters  and
and  are chosen as bifurcation parameters. Consider the following perturbed system:
are chosen as bifurcation parameters. Consider the following perturbed system:

where  and
and  are positive constants while (H1) and (H2) are satisfied. That is to say,
are positive constants while (H1) and (H2) are satisfied. That is to say,

 and
and  are in the small neighborhood of
are in the small neighborhood of  ;
;  and
and  are in the small neighborhood of
are in the small neighborhood of  , where
, where

Clearly, if  is the degenerate equilibrium
is the degenerate equilibrium  of (1.6). Substituting
of (1.6). Substituting  into (3.10) and using Taylor expansion, we obtain
into (3.10) and using Taylor expansion, we obtain

where  ,
,  ,
,  , are smooth functions of
, are smooth functions of  and
and  at least of order three in variables
at least of order three in variables  . Making the change of variables
. Making the change of variables  to (3.13) and noting the conditions in (3.11) and expressions in (3.12), we have
to (3.13) and noting the conditions in (3.11) and expressions in (3.12), we have

where

 ,
,  , are smooth functions in variables
, are smooth functions in variables  at least of the third order, and the coefficients depend smoothly on
at least of the third order, and the coefficients depend smoothly on  and
and  .
.
Let  . Using (3.11) and (3.12), after some algebraic calculations, we obtain
. Using (3.11) and (3.12), after some algebraic calculations, we obtain

where  ,
,  , are smooth functions of
, are smooth functions of  and
and  at least of the third order in variables
at least of the third order in variables  ,
,

Let  . Then (3.16) becomes
. Then (3.16) becomes

where

 is smooth function in variables
is smooth function in variables  at least of order three, and all the coefficients depend smoothly on
at least of order three, and all the coefficients depend smoothly on  and
and  .
.
By setting  to (3.18), we obtain
to (3.18), we obtain

where  is smooth function in variables
is smooth function in variables  at least of the third order and
at least of the third order and

Now, introducing a new time variable  to (3.20), which satisfies
to (3.20), which satisfies  , and still writing
, and still writing  as
as  , we have
, we have

where  is smooth function of
is smooth function of  ,
,  and
and  at least of three order in variables
at least of three order in variables  . Setting
. Setting  to (3.22), we obtain
to (3.22), we obtain

where  is smooth function of
is smooth function of  ,
,  and
and  at least of order three in variables
at least of order three in variables  and
and

If  and
and  , it is easy to obtain the following results:
, it is easy to obtain the following results:

By setting  and
and  , and rewriting
, and rewriting  as
as  , we obtain
, we obtain

where

and  is smooth function of
is smooth function of  ,
,  and
and  at least of order three in variables
at least of order three in variables  .
.
By the theorem of Bogdanov in [26, 27] and the result of Perko in [25], we obtain the following local representations of bifurcation curves in a small neighborhood  of the origin (i.e.,
of the origin (i.e.,  of (1.6).
of (1.6).
Theorem 3.2.
Let the assumptions (H1) and (H2) hold. Then (1.6) admits the following bifurcation behaviors:
-
(i)
there is a saddle-node bifurcation curve
 ;
; -
(ii)
there is a Hopf bifurcation curve
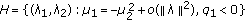 ;
; -
(iii)
there is a homoclinic-loop bifurcation curve HL
 .
.
Concretely, as the statement in [28, Chapter  ], when
], when  , the orbital topical structure of the system (3.26) at origin (corresponding system (1.6) at
, the orbital topical structure of the system (3.26) at origin (corresponding system (1.6) at  ) is shown in Figure 1.
) is shown in Figure 1.
4. Discussion
Note that most infection experiments suggest that the infection rate of microparasitic infections is an increasing function of the parasite dose, usually sigmoidal in shape. In this paper, we study a viral infection model with a type of nonlinear infection rate, which was introduced by Regoes et al. [11].
Qualitative analysis (Theorem 2.1) implies that infection equilibrium  is always stable if the virus is noncytopathic,
is always stable if the virus is noncytopathic,  , or cytopathic in vivo but its cytopathic effect is less than or equal to an appropriate value,
, or cytopathic in vivo but its cytopathic effect is less than or equal to an appropriate value,  . When the cytopathic effect of virus is greater than the threshold value,
. When the cytopathic effect of virus is greater than the threshold value,  , the stability of the infection equilibrium
, the stability of the infection equilibrium  depends on the value of parameter
depends on the value of parameter  , which is proportional to the birth rate of susceptible cells
, which is proportional to the birth rate of susceptible cells  and is in inverse proportion to the infectious dose
and is in inverse proportion to the infectious dose  . The infection equilibrium is stable if
. The infection equilibrium is stable if  and becomes unstable if
and becomes unstable if  . When
. When  gets to the critical value,
gets to the critical value,  , the infection equilibrium is a linear center, so the oscillation behaviors may occur.
, the infection equilibrium is a linear center, so the oscillation behaviors may occur.
If our model (1.6) does not have a limit cycle (see Theorem 2.2 and Corollary 2.3), its asymptotic behavior is determined by the stability of  . When
. When  is stable, there is a region outside which positive semiorbits tend to
is stable, there is a region outside which positive semiorbits tend to  as
as  tends to infinity and inside which positive semi-orbits tend to
tends to infinity and inside which positive semi-orbits tend to  as
as  tends to infinity; that is, the virus will persist if the initial position lies in the region and disappear if the initial position lies outside this region. Thus, besides the value of parameters, the initial concentration of the virus can also affect the result of invasion. An invasion threshold may exist in these cases, which is typical for the so-called Allee effect that occurs when the abundance or frequency of a species is positively correlated with its growth rate (see [11]). Consequently, the unrescaled model (1.5) can display an Allee effect (see Figure 2), which is an infrequent phenomenon in current viral infection models though it is reasonable and important in viral infection process.
tends to infinity; that is, the virus will persist if the initial position lies in the region and disappear if the initial position lies outside this region. Thus, besides the value of parameters, the initial concentration of the virus can also affect the result of invasion. An invasion threshold may exist in these cases, which is typical for the so-called Allee effect that occurs when the abundance or frequency of a species is positively correlated with its growth rate (see [11]). Consequently, the unrescaled model (1.5) can display an Allee effect (see Figure 2), which is an infrequent phenomenon in current viral infection models though it is reasonable and important in viral infection process.
Illustrations of the Allee effect for (1. 5). Here,  .
.  is stable,
is stable,  is a saddle point,
is a saddle point,  is stable. Note that SM is the stable manifolds of
is stable. Note that SM is the stable manifolds of  (solid line), UM is the unstable manifolds of
(solid line), UM is the unstable manifolds of  (dash line), and the phase portrait of (1.6) is divided into two domains of extinction and persistence of the virus by SM.
(dash line), and the phase portrait of (1.6) is divided into two domains of extinction and persistence of the virus by SM.
Furthermore, when infection equilibrium becomes a degenerate singular point, we have shown that the dynamics of this model are very rich inside this region (see Theorems 3.1 and 3.2 and Figure 1). Static and dynamical bifurcations, including saddle-node bifurcation, Hopf bifurcation, homoclinic bifurcation, and bifurcation of cusp-type with codimension two (i.e., Bogdanov-Takens bifurcation), have been exhibited. Thus, besides the Allee effect, our model (1.6) shows that the viral oscillation behaviors can occur in the host based on the appropriate conditions, which was observed in chronic HBV or HCV carriers (see [29–31]). These results inform that the viral infection is very complex in the development of a better understanding of diseases. According to the analysis, we find that the cytopathic effect of virus and the birth rate of susceptible cells are both significant to induce the complex and interesting phenomena, which is helpful in the development of various drug therapy strategies against viral infection.
References
Nowak MA, May RM: Virus Dynamics. Oxford University Press, Oxford, UK; 2000:xii+237.
Wang K, Wang W: Propagation of HBV with spatial dependence. Mathematical Biosciences 2007, 210(1):78-95. 10.1016/j.mbs.2007.05.004
Campos D, Méndez V, Fedotov S: The effects of distributed life cycles on the dynamics of viral infections. Journal of Theoretical Biology 2008, 254(2):430-438. 10.1016/j.jtbi.2008.05.035
Srivastava PKr, Chandra P:Modeling the dynamics of HIV and
 T cells during primary infection. Nonlinear Analysis: Real World Applications. In press
T cells during primary infection. Nonlinear Analysis: Real World Applications. In pressBartholdy C, Christensen JP, Wodarz D, Thomsen AR: Persistent virus infection despite chronic cytotoxic T-lymphocyte activation in gamma interferon-deficient mice infected with lymphocytic choriomeningitis virus. Journal of Virology 2000, 74(22):10304-10311. 10.1128/JVI.74.22.10304-10311.2000
Bonhoeffer S, Coffin JM, Nowak MA: Human immunodeficiency virus drug therapy and virus load. Journal of Virology 1997, 71(4):3275-3278.
Wodarz D, Christensen JP, Thomsen AR: The importance of lytic and nonlytic immune responses in viral infections. Trends in Immunology 2002, 23(4):194-200. 10.1016/S1471-4906(02)02189-0
Perelson AS, Nelson PW: Mathematical analysis of HIV-1 dynamics in vivo. SIAM Review 1999, 41(1):3-44. 10.1137/S0036144598335107
Ebert D, Zschokke-Rohringer CD, Carius HJ: Dose effects and density-dependent regulation of two microparasites of Daphnia magna. Oecologia 2000, 122(2):200-209. 10.1007/PL00008847
McLean AR, Bostock CJ: Scrapie infections initiated at varying doses: an analysis of 117 titration experiments. Philosophical Transactions of the Royal Society B 2000, 355(1400):1043-1050. 10.1098/rstb.2000.0641
Regoes RR, Ebert D, Bonhoeffer S: Dose-dependent infection rates of parasites produce the Allee effect in epidemiology. Proceedings of the Royal Society B 2002, 269(1488):271-279. 10.1098/rspb.2001.1816
Gao S, Chen L, Nieto JJ, Torres A: Analysis of a delayed epidemic model with pulse vaccination and saturation incidence. Vaccine 2006, 24(35-36):6037-6045. 10.1016/j.vaccine.2006.05.018
Ruan S, Wang W: Dynamical behavior of an epidemic model with a nonlinear incidence rate. Journal of Differential Equations 2003, 188(1):135-163. 10.1016/S0022-0396(02)00089-X
Ruan S, Xiao D: Global analysis in a predator-prey system with nonmonotonic functional response. SIAM Journal on Applied Mathematics 2001, 61(4):1445-1472. 10.1137/S0036139999361896
Sharomi O, Gumel AB: Re-infection-induced backward bifurcation in the transmission dynamics of Chlamydia trachomatis . Journal of Mathematical Analysis and Applications 2009, 356(1):96-118. 10.1016/j.jmaa.2009.02.032
Wang W: Epidemic models with nonlinear infection forces. Mathematical Biosciences and Engineering 2006, 3(1):267-279.
Zhang H, Chen L, Nieto JJ: A delayed epidemic model with stage-structure and pulses for pest management strategy. Nonlinear Analysis: Real World Applications 2008, 9(4):1714-1726. 10.1016/j.nonrwa.2007.05.004
Li D, Ma W: Asymptotic properties of a HIV-1 infection model with time delay. Journal of Mathematical Analysis and Applications 2007, 335(1):683-691. 10.1016/j.jmaa.2007.02.006
Song X, Neumann AU: Global stability and periodic solution of the viral dynamics. Journal of Mathematical Analysis and Applications 2007, 329(1):281-297. 10.1016/j.jmaa.2006.06.064
Cai L, Wu J: Analysis of an HIV/AIDS treatment model with a nonlinear incidence. Chaos, Solitons & Fractals 2009, 41(1):175-182. 10.1016/j.chaos.2007.11.023
Wang W, Shen J, Nieto JJ: Permanence and periodic solution of predator-prey system with Holling type functional response and impulses. Discrete Dynamics in Nature and Society 2007, 2007:-15.
Wang X, Song X:Global stability and periodic solution of a model for HIV infection of
 T cells. Applied Mathematics and Computation 2007, 189(2):1331-1340. 10.1016/j.amc.2006.12.044
T cells. Applied Mathematics and Computation 2007, 189(2):1331-1340. 10.1016/j.amc.2006.12.044Yang J: Dynamics behaviors of a discrete ratio-dependent predator-prey system with Holling type III functional response and feedback controls. Discrete Dynamics in Nature and Society 2008, 2008:-19.
van den Driessche P, Watmough J: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences 2002, 180: 29-48. 10.1016/S0025-5564(02)00108-6
Perko L: Differential Equations and Dynamical Systems, Texts in Applied Mathematics. Volume 7. 2nd edition. Springer, New York, NY, USA; 1996:xiv+519.
Bogdanov R: Bifurcations of a limit cycle for a family of vector fields on the plan. Selecta Mathematica Sovietica 1981, 1: 373-388.
Bogdanov R: Versal deformations of a singular point on the plan in the case of zero eigenvalues. Selecta Mathematica Sovietica 1981, 1: 389-421.
Zhang Z, Li C, Zheng Z, Li W: The Base of Bifurcation Theory about Vector Fields. Higher Education Press, Beijing, China; 1997.
Chun YK, Kim JY, Woo HJ, et al.: No significant correlation exists between core promoter mutations, viral replication, and liver damage in chronic hepatitis B infection. Hepatology 2000, 32(5):1154-1162. 10.1053/jhep.2000.19623
Deng G-H, Wang Z-L, Wang Y-M, Wang K-F, Fan Y: Dynamic determination and analysis of serum virus load in patients with chronic HBV infection. World Chinese Journal of Digestology 2004, 12(4):862-865.
Pontisso P, Bellati G, Brunetto M, et al.: Hepatitis C virus RNA profiles in chronically infected individuals: do they relate to disease activity? Hepatology 1999, 29(2):585-589. 10.1002/hep.510290240
Acknowledgments
This work is supported by the National Natural Science Fund of China (nos. 30770555 and 10571143), the Natural Science Foundation Project of CQ CSTC (2007BB5012), and the Science Fund of Third Military Medical University (06XG001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, Y., Nieto, J., Torres, A. et al. A Viral Infection Model with a Nonlinear Infection Rate. Bound Value Probl 2009, 958016 (2009). https://doi.org/10.1155/2009/958016
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/958016
 ;
;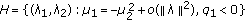 ;
; .
.

 T cells during primary infection. Nonlinear Analysis: Real World Applications. In press
T cells during primary infection. Nonlinear Analysis: Real World Applications. In press T cells. Applied Mathematics and Computation 2007, 189(2):1331-1340. 10.1016/j.amc.2006.12.044
T cells. Applied Mathematics and Computation 2007, 189(2):1331-1340. 10.1016/j.amc.2006.12.044