- Research Article
- Open access
- Published:
Uniqueness and Parameter Dependence of Positive Solution of Fourth-Order Nonhomogeneous BVPs
Boundary Value Problems volume 2010, Article number: 106962 (2010)
Abstract
We investigate the following fourth-order four-point nonhomogeneous Sturm-Liouville boundary value problem:  ,
,  ,
,  , where
, where  and
and  are nonnegative parameters. Some sufficient conditions are given for the existence and uniqueness of a positive solution. The dependence of the solution on the parameters
are nonnegative parameters. Some sufficient conditions are given for the existence and uniqueness of a positive solution. The dependence of the solution on the parameters  is also studied.
is also studied.
1. Introduction
Boundary value problems (BVPs for short) consisting of fourth-order differential equation and four-point homogeneous boundary conditions have received much attention due to their striking applications. For example, Chen et al. [1] studied the fourth-order nonlinear differential equation

with the four-point homogeneous boundary conditions


where  . By means of the upper and lower solution method and Schauder fixed point theorem, some criteria on the existence of positive solutions to the BVP (1.1)–(1.3) were established. Bai et al. [2] obtained the existence of solutions for the BVP (1.1)–(1.3) by using a nonlinear alternative of Leray-Schauder type. For other related results, one can refer to [3–5] and the references therein.
. By means of the upper and lower solution method and Schauder fixed point theorem, some criteria on the existence of positive solutions to the BVP (1.1)–(1.3) were established. Bai et al. [2] obtained the existence of solutions for the BVP (1.1)–(1.3) by using a nonlinear alternative of Leray-Schauder type. For other related results, one can refer to [3–5] and the references therein.
Recently, nonhomogeneous BVPs have attracted many authors' attention. For instance, Ma [6, 7] and L. Kong and Q. Kong [8–10] studied some second-order multipoint nonhomogeneous BVPs. In particular, L. Kong and Q. Kong [10] considered the following second-order BVP with multipoint nonhomogeneous boundary conditions

where  and
and  are nonnegative parameters. They derived some conditions for the above BVP to have a unique solution and then studied the dependence of this solution on the parameters
are nonnegative parameters. They derived some conditions for the above BVP to have a unique solution and then studied the dependence of this solution on the parameters  and
and  . Sun [11] discussed the existence and nonexistence of positive solutions to a class of third-order three-point nonhomogeneous BVP. The authors in [12] studied the multiplicity of positive solutions for some fourth-order two-point nonhomogeneous BVP by using a fixed point theorem of cone expansion/compression type. For more recent results on higher-order BVPs with nonhomogeneous boundary conditions, one can see [13–16].
. Sun [11] discussed the existence and nonexistence of positive solutions to a class of third-order three-point nonhomogeneous BVP. The authors in [12] studied the multiplicity of positive solutions for some fourth-order two-point nonhomogeneous BVP by using a fixed point theorem of cone expansion/compression type. For more recent results on higher-order BVPs with nonhomogeneous boundary conditions, one can see [13–16].
Inspired greatly by the above-mentioned excellent works, in this paper we are concerned with the following Sturm-Liouville BVP consisting of the fourth-order differential equation:

and the four-point nonhomogeneous boundary conditions


where  and
and  are nonnegative parameters. Under the following assumptions:
are nonnegative parameters. Under the following assumptions:
(A1)  and
and  are nonnegative constants with
are nonnegative constants with  ,
,  ,
,  ,
,  ,
,  and
and 
(A2)  is continuous and monotone increasing in
is continuous and monotone increasing in  for every
for every  ;
;
(A3) there exists  such that
such that

we prove the uniqueness of positive solution for the BVP (1.5)–(1.7) and study the dependence of this solution on the parameters  .
.
2. Preliminary Lemmas
First, we recall some fundamental definitions.
Definition 2.1.
Let  be a Banach space with norm
be a Banach space with norm  . Then
. Then
(1) a nonempty closed convex set  is said to be a cone if
is said to be a cone if  for all
for all  and
and  , where
, where  is the zero element of
is the zero element of 
(2) every cone  in
in  defines a partial ordering in
defines a partial ordering in  by
by 
(3) a cone  is said to be normal if there exists
is said to be normal if there exists  such that
such that  implies that
implies that 

(4) a cone  is said to be solid if the interior
is said to be solid if the interior  of
of  is nonempty.
is nonempty.
Definition 2.2.
Let  be a solid cone in a real Banach space
be a solid cone in a real Banach space  an operator, and
an operator, and  Then
Then  is called a
is called a  -concave operator if
-concave operator if

Next, we state a fixed point theorem, which is our main tool.
Lemma 2.3 (see [17]).
Assume that  is a normal solid cone in a real Banach space
is a normal solid cone in a real Banach space  and
and  is a
is a  -concave increasing operator. Then
-concave increasing operator. Then  has a unique fixed point in
has a unique fixed point in 
The following two lemmas are crucial to our main results.
Lemma 2.4.
Assume that  and
and  are defined as in (A1) and
are defined as in (A1) and  . Then for any
. Then for any  the BVP consisting of the equation
the BVP consisting of the equation

and the boundary conditions (1.6) and (1.7) has a unique solution

where

Proof.
Let

Then

By (2.5) and (1.6), we know that

On the other hand, in view of (2.5) and (1.7), we have

So, it follows from (2.6) and (2.8) that

which together with (2.7) implies that

Lemma 2.5.
Assume that (A1) holds. Then
(1)  for
for 
(2)  for
for 
(3)  for
for 
3. Main Result
For convenience, we denote  and
and  . In the remainder of this paper, the following notations will be used:
. In the remainder of this paper, the following notations will be used:
(1)  if at least one of
if at least one of  approaches
approaches  ;
;
(2)  if
if  for
for  ;
;
(3)  if
if  for
for  and at least one of them is strict.
and at least one of them is strict.
Let  . Then
. Then  is a Banach space, where
is a Banach space, where  is defined as usual by the sup norm.
is defined as usual by the sup norm.
Our main result is the following theorem.
Theorem 3.1.
Assume that (A1)–(A3) hold. Then the BVP (1.5)–(1.7) has a unique positive solution  for any
for any  , where
, where  . Furthermore, such a solution
. Furthermore, such a solution  satisfies the following properties:
satisfies the following properties:
(P1) 
(P2)  is strictly increasing in
is strictly increasing in  , that is,
, that is,

(P3)  is continuous in
is continuous in  , that is, for any given
, that is, for any given 

Proof.
Let  . Then
. Then  is a normal solid cone in
is a normal solid cone in  with
with  For any
For any  , if we define an operator
, if we define an operator  as follows:
as follows:

then it is not difficult to verify that  is a positive solution of the BVP (1.5)–(1.7) if and only if
is a positive solution of the BVP (1.5)–(1.7) if and only if  is a fixed point of
is a fixed point of  .
.
Now, we will prove that  has a unique fixed point by using Lemma 2.3.
has a unique fixed point by using Lemma 2.3.
First, in view of Lemma 2.5, we know that 
Next, we claim that  is a
is a  -concave operator.
-concave operator.
In fact, for any  and
and  it follows from (3.3) and (A3) that
it follows from (3.3) and (A3) that

which shows that  is
is  -concave.
-concave.
Finally, we assert that  is an increasing operator.
is an increasing operator.
Suppose that  and
and  By (3.3) and (A2), we have
By (3.3) and (A2), we have

which indicates that  is increasing.
is increasing.
Therefore, it follows from Lemma 2.3 that  has a unique fixed point
has a unique fixed point  which is the unique positive solution of the BVP (1.5)–(1.7). The first part of the theorem is proved.
which is the unique positive solution of the BVP (1.5)–(1.7). The first part of the theorem is proved.
In the rest of the proof, we will prove that such a positive solution  satisfies properties (P1), (P2), and (P3).
satisfies properties (P1), (P2), and (P3).
First,

which together with  for
for  implies (P1).
implies (P1).
Next, we show (P2). Assume that  Let
Let

Then  for
for  We assert that
We assert that  Suppose on the contrary that
Suppose on the contrary that  Since
Since  is a
is a  -concave increasing operator and for given
-concave increasing operator and for given  ,
,  is strictly increasing in
is strictly increasing in  , we have
, we have

which contradicts the definition of  Thus, we get
Thus, we get  for
for  And so,
And so,

which indicates that  is strictly increasing in
is strictly increasing in  .
.
Finally, we prove (P3). For any given  we first suppose that
we first suppose that  with
with  From (P2), we know that
From (P2), we know that

Let

Then  and
and  for
for  If we define
If we define

then  and
and

which together with the definition of  implies that
implies that

So,

Therefore,

In view of (3.10) and (3.16), we obtain that

which together with the fact that  as
as  shows that
shows that

Similarly, we can also prove that

Hence, (P3) holds.
References
Chen S, Ni W, Wang C: Positive solution of fourth order ordinary differential equation with four-point boundary conditions. Applied Mathematics Letters 2006,19(2):161-168. 10.1016/j.aml.2005.05.002
Bai C, Yang D, Zhu H: Existence of solutions for fourth order differential equation with four-point boundary conditions. Applied Mathematics Letters 2007,20(11):1131-1136. 10.1016/j.aml.2006.11.013
Graef JR, Yang B: Positive solutions of a nonlinear fourth order boundary value problem. Communications on Applied Nonlinear Analysis 2007,14(1):61-73.
Wu H, Zhang J:Positive solutions of higher-order four-point boundary value problem with
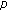 -Laplacian operator. Journal of Computational and Applied Mathematics 2010,233(11):2757-2766. 10.1016/j.cam.2009.06.040
-Laplacian operator. Journal of Computational and Applied Mathematics 2010,233(11):2757-2766. 10.1016/j.cam.2009.06.040Zhao J, Ge W:Positive solutions for a higher-order four-point boundary value problem with a
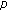 -Laplacian. Computers & Mathematics with Applications 2009,58(6):1103-1112. 10.1016/j.camwa.2009.04.022
-Laplacian. Computers & Mathematics with Applications 2009,58(6):1103-1112. 10.1016/j.camwa.2009.04.022Ma R: Positive solutions for second-order three-point boundary value problems. Applied Mathematics Letters 2001,14(1):1-5. 10.1016/S0893-9659(00)00102-6
Ma R:Positive solutions for nonhomogeneous
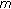 -point boundary value problems. Computers & Mathematics with Applications 2004,47(4-5):689-698. 10.1016/S0898-1221(04)90056-9
-point boundary value problems. Computers & Mathematics with Applications 2004,47(4-5):689-698. 10.1016/S0898-1221(04)90056-9Kong L, Kong Q: Second-order boundary value problems with nonhomogeneous boundary conditions. I. Mathematische Nachrichten 2005,278(1-2):173-193. 10.1002/mana.200410234
Kong L, Kong Q: Second-order boundary value problems with nonhomogeneous boundary conditions. II. Journal of Mathematical Analysis and Applications 2007,330(2):1393-1411. 10.1016/j.jmaa.2006.08.064
Kong L, Kong Q: Uniqueness and parameter dependence of solutions of second-order boundary value problems. Applied Mathematics Letters 2009,22(11):1633-1638. 10.1016/j.aml.2009.05.009
Sun Y: Positive solutions for third-order three-point nonhomogeneous boundary value problems. Applied Mathematics Letters 2009,22(1):45-51. 10.1016/j.aml.2008.02.002
do Ó JM, Lorca S, Ubilla P: Multiplicity of solutions for a class of non-homogeneous fourth-order boundary value problems. Applied Mathematics Letters 2008,21(3):279-286. 10.1016/j.aml.2007.02.025
Graef JR, Kong L, Kong Q, Wong JSW: Higher order multi-point boundary value problems with sign-changing nonlinearities and nonhomogeneous boundary conditions. Electronic Journal of Qualitative Theory of Differential Equations 2010,2010(28):1-40.
Kong L, Kong Q: Higher order boundary value problems with nonhomogeneous boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2010,72(1):240-261. 10.1016/j.na.2009.06.050
Kong L, Piao D, Wang L:Positive solutions for third order boundary value problems with
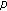 -Laplacian. Results in Mathematics 2009,55(1-2):111-128. 10.1007/s00025-009-0383-z
-Laplacian. Results in Mathematics 2009,55(1-2):111-128. 10.1007/s00025-009-0383-zKong L, Wong JSW: Positive solutions for higher order multi-point boundary value problems with nonhomogeneous boundary conditions. Journal of Mathematical Analysis and Applications 2010,367(2):588-611. 10.1016/j.jmaa.2010.01.063
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgment
Supported by the National Natural Science Foundation of China (10801068).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, JP., Wang, XY. Uniqueness and Parameter Dependence of Positive Solution of Fourth-Order Nonhomogeneous BVPs. Bound Value Probl 2010, 106962 (2010). https://doi.org/10.1155/2010/106962
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/106962
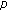 -Laplacian operator. Journal of Computational and Applied Mathematics 2010,233(11):2757-2766. 10.1016/j.cam.2009.06.040
-Laplacian operator. Journal of Computational and Applied Mathematics 2010,233(11):2757-2766. 10.1016/j.cam.2009.06.040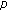 -Laplacian. Computers & Mathematics with Applications 2009,58(6):1103-1112. 10.1016/j.camwa.2009.04.022
-Laplacian. Computers & Mathematics with Applications 2009,58(6):1103-1112. 10.1016/j.camwa.2009.04.022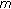 -point boundary value problems. Computers & Mathematics with Applications 2004,47(4-5):689-698. 10.1016/S0898-1221(04)90056-9
-point boundary value problems. Computers & Mathematics with Applications 2004,47(4-5):689-698. 10.1016/S0898-1221(04)90056-9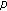 -Laplacian. Results in Mathematics 2009,55(1-2):111-128. 10.1007/s00025-009-0383-z
-Laplacian. Results in Mathematics 2009,55(1-2):111-128. 10.1007/s00025-009-0383-z