- Research Article
- Open access
- Published:
Antiperiodic Solutions for Liénard-Type Differential Equation with 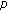 -Laplacian Operator
-Laplacian Operator
Boundary Value Problems volume 2010, Article number: 194824 (2010)
Abstract
The existence of antiperiodic solutions for Liénard-type and Duffing-type differential equations with  -Laplacian operator has been studied by using degree theory. The results obtained improve and enrich some known works to some extent.
-Laplacian operator has been studied by using degree theory. The results obtained improve and enrich some known works to some extent.
1. Introduction
Antiperiodic problems arise naturally from the mathematical models of various of physical processes (see [1, 2]), and also appear in the study of partial differential equations and abstract differential equations (see [3–5]). For instance, electron beam focusing system in travelling-wave tube's theories is an antiperiodic problem (see [6]).
During the past twenty years, antiperiodic problems have been studied extensively by numerous scholars. For example, for first-order ordinary differential equations, a Massera's type criterion was presented in [7] and the validity of the monotone iterative technique was shown in [8]. Moreover, for higher-order ordinary differential equations, the existence of antiperiodic solutions was considered in [9–12]. Recently, existence results were extended to antiperiodic boundary value problems for impulsive differential equations (see [13]), and antiperiodic wavelets were discussed in [14].
Wang and Li (see [15]) discussed the existence of solutions of the following antiperiodic boundary value problem for second-order conservative system:

using of the main assumption as follows:
( ) There exist constants
) There exist constants  and
and  , such that
, such that

The turbulent flow in a porous medium is a fundamental mechanics problem. For studying this type of problems, Leibenson (see [16]) introduced the following  -Laplacian equation:
-Laplacian equation:

where  ,
,  . Obviously, the inverse operator of
. Obviously, the inverse operator of  is
is  , where
, where  is a constant such that
is a constant such that  .
.
Notice that, when  , the nonlinear operator
, the nonlinear operator  reduces to the linear operator
reduces to the linear operator  .
.
In the past few decades, many important results relative to (1.3) with certain boundary conditions have been obtained. We refer the reader to [17–20] and the references cited therein. However, to the best of our knowledge, there exist relatively few results for the existence of antiperiodic solutions of (1.3). Moreover, it is well known that the existence of antiperiodic solutions plays a key role in characterizing the behavior of nonlinear differential equations (see [21]). Thus, it is worthwhile to continue to investigate the existence of antiperiodic solutions for (1.3).
A primary purpose of this paper is to study the existence of antiperiodic solutions for the following Liénard-type  -Laplacian equation:
-Laplacian equation:

and antiperiodic solutions with symmetry for Duffing-type  -Laplacian equation as follows:
-Laplacian equation as follows:

where  ,
,  with
with  ,
,  , and
, and  . That is, we will prove that (1.4) or (1.5) has at least one solution
. That is, we will prove that (1.4) or (1.5) has at least one solution  satisfying
satisfying

Note that,  is also a
is also a  -periodic solution of (1.4) or (1.5) if
-periodic solution of (1.4) or (1.5) if  is a
is a  -antiperiodic solution of (1.4) or (1.5). Hence, from the arguments in this paper, we can also obtain the existence results of periodic solutions for above equations.
-antiperiodic solution of (1.4) or (1.5). Hence, from the arguments in this paper, we can also obtain the existence results of periodic solutions for above equations.
The rest of this paper is organized as follows. Section 2 contains some necessary preliminaries. In Section 3, we establish some sufficient conditions for the existence of antiperiodic solutions of (1.4), basing on Leray-Schauder principle. Then, in Section 4, we obtain two existence results of antiperiodic solutions with symmetry for (1.5). Finally, in Section 5, some explicit examples are given to illustrate the main results. Our results are different from those of bibliographies listed above.
2. Preliminaries
For convenience, we introduce some notations as follows:

and  denotes norm in
denotes norm in  .
.
For each  , there exists the following Fourier series expansion:
, there exists the following Fourier series expansion:

where  . Let us define the mapping
. Let us define the mapping  by
by

Notice that,  may be written as Fourier series as follows:
may be written as Fourier series as follows:

and  may be written as the following Fourier series:
may be written as the following Fourier series:

We define the mapping  by
by

and the mapping  by
by

It is easy to prove that the mappings  are completely continuous by using Arzelà-Ascoli theorem.
are completely continuous by using Arzelà-Ascoli theorem.
Next, we introduce a Wirtinger inequality (see [22]) and a continuation theorem (see [23, 24]) as follows.
Lemma 2.1 (Wirtinger inequality).
For each  such that
such that  and
and  , one has
, one has

where

Lemma 2.2 (Continuation theorem).
Let  be open-bounded in a linear normal space
be open-bounded in a linear normal space  . Suppose that
. Suppose that  is a completely continuous field on
is a completely continuous field on  . Moreover, assume that the Leray-Schauder degree
. Moreover, assume that the Leray-Schauder degree

Then equation  has at least one solution in
has at least one solution in  .
.
3. Antiperiodic Solutions for (1.4)
In this section, an existence result of antiperiodic solutions for (1.4) will be given.
Theorem 3.1.
Assume that
 there exists a nonnegative function
there exists a nonnegative function  such that
such that

where

Then (1.4) has at least one antiperiodic solution.
Remark 3.2.
When  ,
,  is equal to 1. It is easy to see that condition (
is equal to 1. It is easy to see that condition ( ) in [15] is stronger than condition (
) in [15] is stronger than condition ( ) of Theorem 3.1.
) of Theorem 3.1.
For making use of Leray-Schauder degree theory to prove the existence of antiperiodic solutions for (1.4), we consider the homotopic equation of (1.4) as follows:

Define the operator  by
by

where

Let  be the Nemytski operator
be the Nemytski operator

Obviously, the operator  is invertible and the antiperiodic problem of (3.3) is equivalent to the operator equation
is invertible and the antiperiodic problem of (3.3) is equivalent to the operator equation

We begin with some lemmas below.
Lemma 3.3.
Suppose that the assumption  is true. Then the antiperiodic solution
is true. Then the antiperiodic solution  of (3.3) satisfies
of (3.3) satisfies

where  is a positive constant only dependent of
is a positive constant only dependent of  and
and  .
.
Proof.
Multiplying the both sides of (3.3) with  and integrating it over
and integrating it over  , we get
, we get

Noting that

and  , we have
, we have

By hypothesis  , there exists a nonnegative constant
, there exists a nonnegative constant  such that
such that

Thus, from (3.11), we have

That is,

where  .
.
For each  , we get
, we get

Similarly, we obtain that


Basing on Lemma 2.1, it can be shown from (3.17) and (3.14) that

Let  , then
, then

The proof is complete.
Lemma 3.4.
Suppose that the assumption  is true. Then, for the possible antiperiodic solution
is true. Then, for the possible antiperiodic solution  of (3.3), there exists a prior bounds in
of (3.3), there exists a prior bounds in  , that is,
, that is,  satisfies
satisfies

where  is a positive constant independent of
is a positive constant independent of  .
.
Proof.
By (3.15), there exists  such that
such that  . Hence, (3.8) yields that
. Hence, (3.8) yields that

Letting

From (3.16), there exists  such that
such that  , which implies that
, which implies that  . Therefore, integrating the both sides of (3.3) over
. Therefore, integrating the both sides of (3.3) over  , we have
, we have

Thus, we get from (3.8) that

Noting that  , we obtain that
, we obtain that

Combining (3.21) with (3.25), we have

where  . The proof is complete.
. The proof is complete.
Now we give the proof of Theorem 3.1.
Proof of Theorem 3.1..
Setting

Obviously, the set  is an open-bounded set in
is an open-bounded set in  and zero element
and zero element  .
.
From the definition of operator  , it is easy to see that
, it is easy to see that

Hence, the operator  sends
sends  into
into  . Let us define the operator
. Let us define the operator  by
by

Obviously, the operator  is completely continuous in
is completely continuous in  and the fixed points of operator
and the fixed points of operator  are the antiperiodic solutions of (1.4).
are the antiperiodic solutions of (1.4).
With this in mind, let us define the completely continuous field  by
by

By (3.20), we get that zero element  for all
for all  . So that, the following Leray-Schauder degrees are well defined and
. So that, the following Leray-Schauder degrees are well defined and

Consequently, the operator  has at least one fixed point in
has at least one fixed point in  by using Lemma 2.2. Namely, (1.4) has at least one antiperiodic solution. The proof is complete.
by using Lemma 2.2. Namely, (1.4) has at least one antiperiodic solution. The proof is complete.
4. Antiperiodic Solutions with Symmetry for (1.5)
In this section, we will prove the existence of even antiperiodic solutions or odd antiperiodic solutions for (1.5).
Theorem 4.1.
Assume that
 the functions
the functions  and
and  are even in
are even in  , that is,
, that is,

and the assumption ( ) is true. Then (1.5) has at least one even antiperiodic solution
) is true. Then (1.5) has at least one even antiperiodic solution  , that is,
, that is,  satisfies
satisfies

Proof.
We consider the homotopic equation of (1.5) as follows:

Define the operator  by
by

Obviously, the operator  is continuous.
is continuous.
Basing on the proof of Theorem 3.1, for the possible even antiperiodic solution  of (4.3), there exists a prior bounds in
of (4.3), there exists a prior bounds in  , that is,
, that is,  satisfies
satisfies

where  is a positive constant independent of
is a positive constant independent of  . So that, our problem is reduced to construct one completely continuous operator
. So that, our problem is reduced to construct one completely continuous operator  in
in  which sends
which sends  into
into  , such that the fixed points of operator
, such that the fixed points of operator  in some open-bounded set are the even antiperiodic solutions of (1.5).
in some open-bounded set are the even antiperiodic solutions of (1.5).
With this in mind, let us define the following set:

Obviously, the set  is an open-bounded set in
is an open-bounded set in  and zero element
and zero element  .
.
By hypothesis ( ), it is easy to see that
), it is easy to see that

Hence, the operator  sends
sends  into
into  . Let us define the completely continuous operator
. Let us define the completely continuous operator  by
by

From the similar arguments in the proof of Theorem 3.1, we can prove that there exists at least one fixed point of operator  in
in  . Thus, (1.5) has at least one even antiperiodic solution. The proof is complete.
. Thus, (1.5) has at least one even antiperiodic solution. The proof is complete.
Theorem 4.2.
Assume that
 the function
the function  is odd in
is odd in  and
and  is odd in
is odd in  , that is,
, that is,

and the assumption ( ) is true. Then (1.5) has at least one odd antiperiodic solution
) is true. Then (1.5) has at least one odd antiperiodic solution  , that is,
, that is,  satisfies
satisfies

Proof.
We consider the homotopic equation (4.3) of (1.5). Define the operator  by
by

Obviously, the operator  is continuous.
is continuous.
Based on the proof of Theorem 3.1, for the possible odd antiperiodic solutions of (4.3), there exists a prior bounds in  . Hence, our problem is reduced to construct one completely continuous operator
. Hence, our problem is reduced to construct one completely continuous operator  in
in  which sends
which sends  into
into  , such that the fixed points of operator
, such that the fixed points of operator  in some open-bounded set are the odd antiperiodic solutions of (1.5).
in some open-bounded set are the odd antiperiodic solutions of (1.5).
With this in mind, let us define the set as follows:

Obviously, the set  is an open-bounded set in
is an open-bounded set in  and zero element
and zero element  .
.
From the hypothesis ( ), it is easy to see that
), it is easy to see that

Thus, the operator  sends
sends  into
into  . Let us define the completely continuous operator
. Let us define the completely continuous operator  by
by

By a similar way as the proof of Theorem 3.1, we can prove that there exists at least one fixed point of operator  in
in  . So that, (1.5) has at least one odd antiperiodic solution. The proof is complete.
. So that, (1.5) has at least one odd antiperiodic solution. The proof is complete.
5. Examples
In this section, we will give some examples to illustrate our main results.
Consider the following second-order differential equation with  -Laplacian operator:
-Laplacian operator:

Example 5.1.
Let

For  , by direct calculation, we can get
, by direct calculation, we can get  . Choosing
. Choosing  , then (5.1) satisfies the condition of Theorem 3.1. So it has at least one antiperiodic solution.
, then (5.1) satisfies the condition of Theorem 3.1. So it has at least one antiperiodic solution.
Moreover, the conditions of Theorem 4.1 are also satisfied. Thus (5.1) has at least one even antiperiodic solution.
Example 5.2.
Let

We choose  . Obviously, (5.1) satisfies all the conditions of Theorem 4.2. Hence it has at least one odd antiperiodic solution.
. Obviously, (5.1) satisfies all the conditions of Theorem 4.2. Hence it has at least one odd antiperiodic solution.
References
Ahn C, Rim C: Boundary flows in general coset theories. Journal of Physics 1999,32(13):2509-2525.
Kleinert H, Chervyakov A: Functional determinants from Wronski Green functions. Journal of Mathematical Physics 1999,40(11):6044-6051. 10.1063/1.533069
Aizicovici S, McKibben M, Reich S: Anti-periodic solutions to nonmonotone evolution equations with discontinuous nonlinearities. Nonlinear Analysis. Theory, Methods & Applications 2001,43(2):233-251. 10.1016/S0362-546X(99)00192-3
Nakao M: Existence of an anti-periodic solution for the quasilinear wave equation with viscosity. Journal of Mathematical Analysis and Applications 1996,204(3):754-764. 10.1006/jmaa.1996.0465
Souplet P: Optimal uniqueness condition for the antiperiodic solutions of some nonlinear parabolic equations. Nonlinear Analysis. Theory, Methods & Applications 1998,32(2):279-286. 10.1016/S0362-546X(97)00477-X
Lu Z: Travelling Tube. Shanghai Science and Technology Press, Shanghai, China; 1962.
Chen YQ: On Massera's theorem for anti-periodic solution. Advances in Mathematical Sciences and Applications 1999,9(1):125-128.
Yin Y: Monotone iterative technique and quasilinearization for some anti-periodic problems. Nonlinear World 1996,3(2):253-266.
Aftabizadeh AR, Pavel NH, Huang YK: Anti-periodic oscillations of some second-order differential equations and optimal control problems. Journal of Computational and Applied Mathematics 1994,52(1–3):3-21.
Chen T, Liu W, Zhang J, Zhang M: The existence of anti-periodic solutions for Liénard equations. Journal of Mathematical Study 2007,40(2):187-195.
Liu B: Anti-periodic solutions for forced Rayleigh-type equations. Nonlinear Analysis. Real World Applications 2009,10(5):2850-2856. 10.1016/j.nonrwa.2008.08.011
Liu WB, Zhang JJ, Chen TY: Anti-symmetric periodic solutions for the third order differential systems. Applied Mathematics Letters. An International Journal of Rapid Publication 2009,22(5):668-673. 10.1016/j.aml.2008.08.004
Luo Z, Shen J, Nieto JJ: Antiperiodic boundary value problem for first-order impulsive ordinary differential equations. Computers & Mathematics with Applications 2005,49(2-3):253-261. 10.1016/j.camwa.2004.08.010
Chen HL: Antiperiodic wavelets. Journal of Computational Mathematics 1996,14(1):32-39.
Wang K, Li Y: A note on existence of (anti-)periodic and heteroclinic solutions for a class of second-order odes. Nonlinear Analysis. Theory, Methods & Applications 2009,70(4):1711-1724. 10.1016/j.na.2008.02.054
Leibenson LS: General problem of the movement of a compressible fluid in a porous medium. Izvestiia Akademii Nauk Kirgizskoĭ SSSR 1983, 9: 7-10.
Jiang D, Gao W: Upper and lower solution method and a singular boundary value problem for the one-dimensional p -Laplacian. Journal of Mathematical Analysis and Applications 2000,252(2):631-648. 10.1006/jmaa.2000.7012
Lian LF, Ge WG: The existence of solutions of m-point p -Laplacian boundary value problems at resonance. Acta Mathematicae Applicatae Sinica 2005,28(2):288-295.
Liu B, Yu JS: On the existence of solution for the periodic boundary value problems with p -Laplacian operator. Journal of Systems Science and Mathematical Sciences 2003,23(1):76-85.
Zhang J, Liu W, Ni J, Chen T: Multiple periodic solutions of p -Laplacian equation with one-side Nagumo condition. Journal of the Korean Mathematical Society 2008,45(6):1549-1559. 10.4134/JKMS.2008.45.6.1549
Chen Y, Nieto JJ, O'Regan D: Anti-periodic solutions for fully nonlinear first-order differential equations. Mathematical and Computer Modelling 2007,46(9-10):1183-1190. 10.1016/j.mcm.2006.12.006
Croce G, Dacorogna B: On a generalized Wirtinger inequality. Discrete and Continuous Dynamical Systems 2003,9(5):1329-1341.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Gaines RE, Mawhin JL: Coincidence Degree and Nonlinear Differential Equations, Lecture Notes in Mathematics, Vol. 568. Springer, Berlin, Germany; 1977:i+262.
Acknowledgments
The authors would like to thank the referees very much for their helpful comments and suggestions. This research was supported by the National Natural Science Foundation of China (10771212), the Fundamental Research Funds for the Central Universities, and the Science Foundation of China University of Mining and Technology (2008A037).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, T., Liu, W. & Yang, C. Antiperiodic Solutions for Liénard-Type Differential Equation with 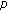 -Laplacian Operator.
Bound Value Probl 2010, 194824 (2010). https://doi.org/10.1155/2010/194824
-Laplacian Operator.
Bound Value Probl 2010, 194824 (2010). https://doi.org/10.1155/2010/194824
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/194824