- Research Article
- Open access
- Published:
Exact Multiplicity of Positive Solutions for a Class of Second-Order Two-Point Boundary Problems with Weight Function
Boundary Value Problems volume 2010, Article number: 207649 (2010)
Abstract
An exact multiplicity result of positive solutions for the boundary value problems  ,
,  ,
,  ,
,  is achieved, where
is achieved, where  is a positive parameter. Here the function
is a positive parameter. Here the function  is
is  and satisfies
and satisfies  ,
,  for
for  for some
for some  . Moreover,
. Moreover,  is asymptotically linear and
is asymptotically linear and  can change sign only once. The weight function
can change sign only once. The weight function  is
is  and satisfies
and satisfies  ,
,  for
for  . Using bifurcation techniques, we obtain the exact number of positive solutions of the problem under consideration for
. Using bifurcation techniques, we obtain the exact number of positive solutions of the problem under consideration for  lying in various intervals in
lying in various intervals in  . Moreover, we indicate how to extend the result to the general case.
. Moreover, we indicate how to extend the result to the general case.
1. Introduction
Consider the problem

where  is a parameter and
is a parameter and  is a weight function.
is a weight function.
The existence and multiplicity of positive solutions for ordinary differential equations have been studied extensively in many literatures, see, for example, [1–3] and references therein. Several different approaches, such as the Leray-Schauder theory, the fixed-point theory, the lower and upper solutions theory, and the shooting method etc has been applied in these literatures. In [4, 5], Ma and Thompson obtained the multiplicity results for a class of second-order two-point boundary value problems depending on a positive parameter  by using bifurcation theory.
by using bifurcation theory.
Exact multiplicity of positive solutions have been studied by many authors. See, for example, the papers by Korman et al. [6], Ouyang and Shi [7, 8], Shi [9], Korman and Ouyang [10, 11], Korman [12], Rynne [13], Bari and Rynne [14] (for  th-order problems), as well as Korman and Li [15]. In these papers, bifurcation techniques are used. The basic method of proving their results can be divided into three steps: proving positivity of solutions of the linearized problems; studying the direction of bifurcation; showing uniqueness of solution curves.
th-order problems), as well as Korman and Li [15]. In these papers, bifurcation techniques are used. The basic method of proving their results can be divided into three steps: proving positivity of solutions of the linearized problems; studying the direction of bifurcation; showing uniqueness of solution curves.
Ouyang and Shi [7] obtained the curves of positive solutions for the semilinear problem

where  is the unit ball in
is the unit ball in  and
and  . In [7], the following two cases were considered:
. In [7], the following two cases were considered:
-
(i)
 does not change its sign on
does not change its sign on 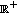 ; (ii)
; (ii)  changes its sign only once on
changes its sign only once on  .
.
Korman and Ouyang [10] studied the problem

under the conditions  and
and

They obtained a full description of the positive solution set of (1.3) and proved that all positive solutions of (1.3) lie on a single smooth solution curve bifurcating from the point  and tending to
and tending to  in the
in the  plane. Condition (1.4) is very important to conclude the direction of bifurcation curve.
plane. Condition (1.4) is very important to conclude the direction of bifurcation curve.
Of course a natural question is how about the structure of the positive solution set of (1.3) when  changes its sign only once on
changes its sign only once on  ?
?
It is extremely difficult to answer such a question in general. So we shift our study to the problem (1.1) in this paper. We are interested in discussing the exact multiplicity of positive solutions of (1.1) with a weight function  when
when  changes its sign only once on
changes its sign only once on  .
.
Suppose the following.
(H1) One has  with
with  for some
for some  and
and  for
for  .
.
(H2)  is concave convex that is, there exists
is concave convex that is, there exists  such that
such that

(H3) The limits  and
and  .
.
(H4)  satisfies
satisfies  and
and  if
if 
In this paper, we obtain exactly two disjoint smooth curves of positive solutions of (1.1) under conditions (H1)–(H4). According to this, we can conclude the existence and exact numbers of positive solutions of (1.1) for  lying in various intervals in
lying in various intervals in  .
.
Remark 1.1.
Korman and Ouyang [10] obtained the unique positive solution curve of (1.3) under the condition (1.4). However they gave no information when  can change sign. In [7], they did not treat the case that the equation contains a weight function.
can change sign. In [7], they did not treat the case that the equation contains a weight function.
On the other hand, suppose the following.
(H1′) One has  with
with  . There exists
. There exists  such that
such that  and
and  .
.
Remark 1.2.
If  , then we know from the proof in [4] that the assumptions (H1
, then we know from the proof in [4] that the assumptions (H1 ) and (H3) imply that the component of positive solutions from the trivial solution and the component from infinity are coincident. However, these two components are disjoint under the assumptions (H1) and (H3) (see [5]). Hence, the essential role is played by the fact of whether
) and (H3) imply that the component of positive solutions from the trivial solution and the component from infinity are coincident. However, these two components are disjoint under the assumptions (H1) and (H3) (see [5]). Hence, the essential role is played by the fact of whether  possesses zeros in
possesses zeros in  ∖
∖ . In Section 3, we prove that (1.1) has exactly two positive solution curves which are disjoint and have no turning point on them (Theorem 3.8) under Conditions (H1)–(H4). And (1.1) has a unique positive solution curve with only one turning point (Theorem 3.9) if (H1) is replaced by (H1
. In Section 3, we prove that (1.1) has exactly two positive solution curves which are disjoint and have no turning point on them (Theorem 3.8) under Conditions (H1)–(H4). And (1.1) has a unique positive solution curve with only one turning point (Theorem 3.9) if (H1) is replaced by (H1 ). The condition (H4) is used to prove the positivity of solutions of the linearized problems of (1.1) and the direction of bifurcation.
). The condition (H4) is used to prove the positivity of solutions of the linearized problems of (1.1) and the direction of bifurcation.
Our main tool is the following bifurcation theorem of Crandall and Rabinowitz.
Theorem 1.3 (see [16]).
Let  and
and  be Banach spaces. Let
be Banach spaces. Let  and let
and let  be a continuously differentiable mapping of an open neighborhood of
be a continuously differentiable mapping of an open neighborhood of  into
into  . Let the null-space
. Let the null-space  be one dimensional and codim
be one dimensional and codim . Let
. Let  . If
. If  is a complement of span
is a complement of span in
in  , then the solution of
, then the solution of  near
near  forms a curve
forms a curve  , where
, where  is a continuously differentiable function near
is a continuously differentiable function near  and
and  .
.
2. Notations and Preliminaries
Let  with the norm
with the norm

and let

with the norm

Set

equipped with the norm

Define the operator  ,
,

Then,  is a completely continuous operator.
is a completely continuous operator.
Definition 2.1.
For a nontrivial solution of (1.1),  is degenerate if the linearized problem
is degenerate if the linearized problem

has a nontrivial solution; otherwise, it is nondegenerate.
Lemma 2.2.
Let (H1) and (H4) hold. For any degenerate positive solution  of (1.1), the nontrivial solution
of (1.1), the nontrivial solution  of (2.7) can be chosen as positive.
of (2.7) can be chosen as positive.
Proof.
The proof is motivated by Lemma  in [11].
in [11].
Suppose to the contrary that  has zeros on (0,1). Without loss of generality, suppose that
has zeros on (0,1). Without loss of generality, suppose that  . Note that
. Note that  and
and  satisfy
satisfy


respectively. We claim that  has at most one zero in (0,1). Otherwise, let
has at most one zero in (0,1). Otherwise, let  be the first two zeros of
be the first two zeros of  . Then,
. Then,

Multiplying (2.9) by  and (2.8) by
and (2.8) by  , subtracting, and integrating over
, subtracting, and integrating over  , we have
, we have

with  to be specified. We denote the left side of (2.11) by
to be specified. We denote the left side of (2.11) by  and a constant
and a constant  by
by  . Integrating by parts,
. Integrating by parts,

Let

on  From (2.10), (2.13), and
From (2.10), (2.13), and  , we have
, we have

Note that the right side of (2.11) is zero, which is a contradiction.
Hence,  has at most one zero in (0,1). Suppose that there is one point
has at most one zero in (0,1). Suppose that there is one point  such that
such that  . Then,
. Then,

Repeating the above proof on  , we can get similar contradiction.
, we can get similar contradiction.
Finally, integrating the differential equation in (2.13), we can choose

In view of (H4),  . So, the auxiliary function
. So, the auxiliary function  exists.
exists.
The following lemma is an important result in this paper.
Lemma 2.3.
Let (H1) and (H4) hold. Suppose that  is a degenerate positive solution of (1.1). Then, the following are considered.
is a degenerate positive solution of (1.1). Then, the following are considered.
(i) All solutions of (1.1) near  have the form
have the form  for
for  and some
and some  , where
, where 
 .
.
(ii) One has  if
if  is concave convex;
is concave convex;  if
if  is convex concave.
is convex concave.
Proof.
-
(i)
The proof is standard. Let
 be such that
be such that 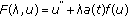 . We will show that the conditions of Theorem 1.3 hold.
. We will show that the conditions of Theorem 1.3 hold.
Since  is a degenerate positive solution of (1.1), we denote the corresponding solution of (2.7) by
is a degenerate positive solution of (1.1), we denote the corresponding solution of (2.7) by  . From Lemma 2.2 and the theory of compact disturbing of a Fredholm operator,
. From Lemma 2.2 and the theory of compact disturbing of a Fredholm operator,  is one dimensional and codim
is one dimensional and codim .
.
Now, we show that  . Suppose to the contrary that
. Suppose to the contrary that  . Then, there is a
. Then, there is a  such that
such that


Note that  satisfies
satisfies


Multiplying (2.17) by  and (2.19) by
and (2.19) by  , subtracting, and integrating on both sides, we obtain
, subtracting, and integrating on both sides, we obtain

However, the left side of (2.21) is equal to zero according to boundary conditions (2.18) and (2.20). This implies that  . According to Theorem 1.3, the result (i) holds.
. According to Theorem 1.3, the result (i) holds.
-
(ii)
Substituting
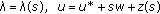 into (1.1), we obtain
into (1.1), we obtain 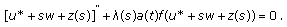 (2.22)
(2.22)
Since  then, by the implicit function theorem, the solution curve near
then, by the implicit function theorem, the solution curve near  is also
is also  Differentiating (2.22) twice with respect to
Differentiating (2.22) twice with respect to  , we have
, we have

Evaluating at  , we obtain
, we obtain

Multiplying (2.24) by  and (2.19) by
and (2.19) by  , subtracting, and integrating, we get
, subtracting, and integrating, we get

According to (H1), (H4), and Lemma 2.2, we see that  . Next, for the sign of
. Next, for the sign of  , we consider the sign of
, we consider the sign of  .
.
We first prove that

Differentiating (1.1) and (2.19) with respect to  , we have
, we have


Multiplying, (2.27) by  and (2.28) by
and (2.28) by  , subtracting, and integrating over
, subtracting, and integrating over  , we get
, we get

with  to be specified. Integrating by parts on the left side of (2.29),
to be specified. Integrating by parts on the left side of (2.29),

Let

From (2.29), we get

Solving the equation  , we can choose the auxiliary function
, we can choose the auxiliary function

Combining with (2.32), we obtain (2.26).
The following proof is motivated by the proof of Theorem  in [8].
in [8].
Since  , (2.26) implies that
, (2.26) implies that  must change sign. If
must change sign. If  is concave convex, then there exists
is concave convex, then there exists  such that
such that

Next, we claim that there exists  , such that
, such that

Let  . Then,
. Then,  , and
, and  . So,
. So,  has at least one zero in
has at least one zero in  . Moreover, we can prove that
. Moreover, we can prove that  has only one zero in
has only one zero in  . Note that
. Note that  satisfies
satisfies

We get

since  and
and  . Suppose that
. Suppose that  has more than one zero in (0, 1). Let
has more than one zero in (0, 1). Let  be the last two zeros of
be the last two zeros of  , then we say that
, then we say that

We first prove the above statement. On the contrary, suppose that

Consider the problem

Obviously,  is a subsolution and
is a subsolution and  is a supersolution of (2.40), respectively. Note that
is a supersolution of (2.40), respectively. Note that  . By the strong maximum principle, we obtain that
. By the strong maximum principle, we obtain that  on
on  . This contradicts
. This contradicts  . Hence, the statement holds.
. Hence, the statement holds.
Now let us consider the claim related to  . Multiplying (2.36) by
. Multiplying (2.36) by  and (2.37) by
and (2.37) by  , subtracting, and integrating over
, subtracting, and integrating over  , we get
, we get

since  . Note that the left side is nonnegative. Such a contradiction implies that
. Note that the left side is nonnegative. Such a contradiction implies that  has only one zero in (0,1). By varying
has only one zero in (0,1). By varying  such that
such that  we can conclude the claim.
we can conclude the claim.
From the claim and  , we have
, we have

Hence,  from (2.25).
from (2.25).
If  is convex concave, then
is convex concave, then  with a similar proof.
with a similar proof.
3. The Main Results and the Proofs
In this section we state our main results and proofs.
Definition 3.1.
Define

where  is the first eigenvalue of the corresponding linear problem
is the first eigenvalue of the corresponding linear problem

Remark 3.2.
It is well known that the eigenvalues of (3.2) are given by

For each  , algebraic multiplicity of
, algebraic multiplicity of  is equal to 1, and the corresponding eigenfunction
is equal to 1, and the corresponding eigenfunction  has exactly
has exactly  simple zeros in
simple zeros in  .
.
Definition 3.3 (see [7]).
Let  . Then
. Then  is said to be superlinear (resp., sublinear) on
is said to be superlinear (resp., sublinear) on  if
if  (resp.,
(resp.,  ) on
) on  . And
. And  is said to be sup-sub (resp., sub-sup) on
is said to be sup-sub (resp., sub-sup) on  if there exists
if there exists  such that
such that  is superlinear (resp., sublinear) on
is superlinear (resp., sublinear) on  , and superlinear (resp., sublinear) on
, and superlinear (resp., sublinear) on  .
.
Lemma 3.4.
-
(i)
Let
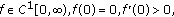 and (H4) hold. Suppose that
and (H4) hold. Suppose that 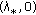 is a point where a bifurcation from the trivial solutions occurs and that
is a point where a bifurcation from the trivial solutions occurs and that  is the corresponding positive solution bifurcation curve of (1.1). If there exists
is the corresponding positive solution bifurcation curve of (1.1). If there exists  such that
such that 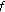 is superlinear (resp., sublinear) on
is superlinear (resp., sublinear) on 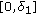 , then
, then  tends to the left (resp., the right) near
tends to the left (resp., the right) near  .
. -
(ii)
Let
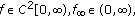 and (H4) hold. Suppose that
and (H4) hold. Suppose that  is a point where a bifurcation from infinity occurs and that
is a point where a bifurcation from infinity occurs and that  is the corresponding positive solution bifurcation curve of (1.1). If there exists
is the corresponding positive solution bifurcation curve of (1.1). If there exists 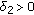 such that
such that  is superlinear (resp., sublinear) on
is superlinear (resp., sublinear) on 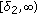 and
and 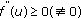 (resp.,
(resp., 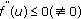 ) for
) for  , then
, then  tends to the right (resp., the left) near
tends to the right (resp., the left) near 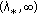 .
.
Proof.
The proof is similar to that of Proposition  in [7], so we omit it.
in [7], so we omit it.
Lemma 3.5.
Let (H1)–(H4) hold, let  be a bounded and closed interval, and let
be a bounded and closed interval, and let  . Suppose that
. Suppose that  are positive solutions of (1.1). Then,
are positive solutions of (1.1). Then,
(i)  , if
, if  ,
,
(ii)  , if
, if  .
.
Proof.
Let  be such that
be such that

Clearly,

Let us consider

as a bifurcation problem from  . Note that (3.6) is the same as to (1.1). From Remark 3.2 and the standard bifurcation theorem from simple eigenvalues [17], we have (i).
. Note that (3.6) is the same as to (1.1). From Remark 3.2 and the standard bifurcation theorem from simple eigenvalues [17], we have (i).
Let us consider

as a bifurcation problem from infinity. Note that (3.7) is also the same as to (1.1). The proof of Theorem  in [5] ensures that (ii) is correct.
in [5] ensures that (ii) is correct.
Lemma 3.6.
Let (H1), (H4) hold. Suppose that  is a positive solution of (1.1). Then,
is a positive solution of (1.1). Then,

Proof.
Suppose to the contrary that

By (1.1) and (H1), we have  . Note that
. Note that  . By the uniqueness of solutions of initial value problem, the problem
. By the uniqueness of solutions of initial value problem, the problem

has a unique solution  . This contradicts
. This contradicts  .
.
The following Lemma is an interesting and important result.
Lemma 3.7.
Let (H1)–(H4) hold. Suppose that  is a positive solution of (1.1), then
is a positive solution of (1.1), then  is nondegenerate.
is nondegenerate.
Proof.
From conditions (H1)–(H3), we can check easily that

In fact, let  , then
, then

since  . Note that
. Note that  , if
, if  and
and  , if
, if  . This together with (3.12) implies that
. This together with (3.12) implies that  and (3.11).
and (3.11).
Now, we give the proof in two cases.
Case I ( ).
).
On the contrary, suppose that  is a degenerate solution with
is a degenerate solution with  , then
, then  for all
for all . By (3.11), we get
. By (3.11), we get

Multiplying (1.1) by  and (2.7) by
and (2.7) by  , subtracting, and integrating, we have
, subtracting, and integrating, we have

By Lemma 2.2, (3.13), and  for all
for all , the right side of (3.14) is negative. This is a contradiction.
, the right side of (3.14) is negative. This is a contradiction.
Case II ( ).
).
On the contrary, suppose that  is a degenerate solution with
is a degenerate solution with  . According to Lemmas 2.2 and 2.3, we know that all solutions of (1.1) near
. According to Lemmas 2.2 and 2.3, we know that all solutions of (1.1) near  satisfy
satisfy  for
for  and some
and some  , where
, where 
 . It follows that for
. It follows that for  close to
close to  we have two solutions
we have two solutions  and
and  with
with  strictly increasing in
strictly increasing in  and
and  with strictly decreasing in
with strictly decreasing in  . We will show that the lower branch
. We will show that the lower branch  is strictly increasing for all
is strictly increasing for all  .
.
Note that  for
for  close to
close to  and all
and all  . Let
. Let  be the largest
be the largest  where this inequality is violated; that is,
where this inequality is violated; that is,  and
and  for some
for some  . Differentiating (1.1) with respect to
. Differentiating (1.1) with respect to  ,
,

We can extend evenly  , and
, and  on
on  , then we obtain
, then we obtain

By the strong maximum principle, we conclude that  for all
for all  . This contradicts that
. This contradicts that  .
.
By Lemma 2.3, we get  at every degenerate positive solution. Hence, there is no degenerate positive solution on the lower branch
at every degenerate positive solution. Hence, there is no degenerate positive solution on the lower branch  . However, the lower branch has no place to go. In fact, there must exist some positive constant
. However, the lower branch has no place to go. In fact, there must exist some positive constant  such that
such that  for any
for any  lying on
lying on  . Hence, the lower branch cannot go to the
. Hence, the lower branch cannot go to the  axis. And it also cannot go to the
axis. And it also cannot go to the  axis, since (1.1) has only the trivial solution at
axis, since (1.1) has only the trivial solution at  .
.
So,  is nondegenerate.
is nondegenerate.
Our main result is the following.
Theorem 3.8.
Let (H1)–(H4) hold. Then the following are considered.
(i) All positive solutions of (1.1) lie on two continuous curves  and
and  without intersection.
without intersection.  bifurcates from
bifurcates from  to infinity and
to infinity and  ;
;  bifurcates from
bifurcates from  to infinity and
to infinity and  . There is no degenerate positive solution on these curves. For any
. There is no degenerate positive solution on these curves. For any  ,
,  , and for any
, and for any  ,
,  .
.
(ii) Equation (1.1) has no positive solution for  has exactly one positive solution for
has exactly one positive solution for  but and has exactly two positive solutions for
but and has exactly two positive solutions for  (see Figure 1).
(see Figure 1).

Figure 1
Proof.
-
(i)
Since
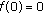 and
and 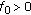 , then
, then  . From Lemma 3.5(i) and the standard Crandall and Rabinowitz theorem on local bifurcation from simple eigenvalues [17],
. From Lemma 3.5(i) and the standard Crandall and Rabinowitz theorem on local bifurcation from simple eigenvalues [17],  is the unique point where a bifurcation from the trivial solution occurs. Moreover, by Lemma 3.4, the curve bifurcates to the right. We denote this local curve by
is the unique point where a bifurcation from the trivial solution occurs. Moreover, by Lemma 3.4, the curve bifurcates to the right. We denote this local curve by 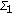 and continue
and continue 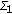 to the right as long as it is possible. Meanwhile, by Lemma 3.6, there is no positive solution of (1.1) which has the maximum value
to the right as long as it is possible. Meanwhile, by Lemma 3.6, there is no positive solution of (1.1) which has the maximum value  on
on 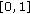 . So, if
. So, if 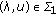 , then
, then 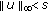 . From (1.1), we have
. From (1.1), we have 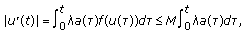 (3.17)
(3.17)
where  . Obviously, there exists a constant
. Obviously, there exists a constant  such that
such that  if
if  is bounded. Hence,
is bounded. Hence,  cannot blow up.
cannot blow up.
On the other hand, Lemma 3.7 and the implicit function theorem ensure that  cannot stop at a finite point
cannot stop at a finite point  .
.
From the above discussion, we see that  can be extended continuously to infinity and
can be extended continuously to infinity and  . Meanwhile, the maximum values of all positive solutions of (1.1) are less than
. Meanwhile, the maximum values of all positive solutions of (1.1) are less than  .
.
Now, we consider positive solutions of (1.1), for which the maximum value on  is greater than
is greater than  .
.
Let us return to consider (3.6) as the bifurcation problem from infinity. Note that (3.6) is also the same as to (1.1). Since  by Theorem
by Theorem  and Corollary
and Corollary  in [18], there exists a subcontinuum
in [18], there exists a subcontinuum  of positive solutions of (3.6) which meets
of positive solutions of (3.6) which meets  . Take
. Take  as an interval such that
as an interval such that  and
and  as a neighborhood of
as a neighborhood of  whose projection on
whose projection on  lies in
lies in  and whose projection on
and whose projection on  is bounded away from
is bounded away from  . Then, there exists a neighborhood
. Then, there exists a neighborhood  such that any positive solution
such that any positive solution  of (1.1) satisfies
of (1.1) satisfies  for
for  and some
and some  and
and  at
at  , where
, where  denotes the normalized eigenvector of (3.2) corresponding to
denotes the normalized eigenvector of (3.2) corresponding to  . So,
. So, 
Hence,  is a continuous curve, and we denote it by
is a continuous curve, and we denote it by  . It tends to the right from Lemma 3.4(ii). From Lemma 3.7 and the implicit function theorem,
. It tends to the right from Lemma 3.4(ii). From Lemma 3.7 and the implicit function theorem,  can be continued to a maximal interval of definition over the
can be continued to a maximal interval of definition over the  axis. We claim that
axis. We claim that  ∖
∖ cannot blow up if
cannot blow up if  is bounded. In fact, suppose that there exists a positive solutions sequence
is bounded. In fact, suppose that there exists a positive solutions sequence  of (1.1) and
of (1.1) and  such that
such that  as
as  . Then, by Lemma 3.5(ii),
. Then, by Lemma 3.5(ii),  . This is a contradiction. On the other hand, the implicit function theorem implies that
. This is a contradiction. On the other hand, the implicit function theorem implies that  cannot stop at a finite point
cannot stop at a finite point  . Thus,
. Thus,  and
and  if
if  .
.
Finally, we show that both curves  and
and  are the only two positive solutions curves of (1.1). On the contrary, suppose that
are the only two positive solutions curves of (1.1). On the contrary, suppose that  is a positive solution of (1.1) with
is a positive solution of (1.1) with  . Without loss of generality, assume that
. Without loss of generality, assume that  . Note that
. Note that  is nondegenerate, so we can extend it to form a curve. We denote this curve by
is nondegenerate, so we can extend it to form a curve. We denote this curve by  and the corresponding maximal interval of definition by
and the corresponding maximal interval of definition by  . Since all positive solutions of (1.1) are nondegenerate, according to the implicit function theorem, we must have that
. Since all positive solutions of (1.1) are nondegenerate, according to the implicit function theorem, we must have that

It follows that  from Lemma 3.5(ii). But all solutions near
from Lemma 3.5(ii). But all solutions near  can be parameterized by
can be parameterized by  for
for  and some
and some  ; thus,
; thus,  . This contradicts that
. This contradicts that  .
.
Similarly, we can show that every positive solution of (1.1), the maximum value on  of which is less than
of which is less than  lies on
lies on  .
.
-
(ii)
The result (ii) is a corollary of (i).
Next, we will give directly other theorems. Their proofs are similar to that of Theorem 3.8. So, we omit them.
Theorem 3.9.
Let  and (H2)–(H4) hold. Then, the following are considered.
and (H2)–(H4) hold. Then, the following are considered.
(i) All positive solutions of (1.1) lie on a single continuous curve  . And
. And  bifurcates from
bifurcates from  to the right to a unique degenerate positive solution
to the right to a unique degenerate positive solution  of (1.1), then it tends to the left to
of (1.1), then it tends to the left to  .
.
(ii) Equation (1.1) has no positive solution for  , and has exactly one positive solution for
, and has exactly one positive solution for  , and has exactly two positive solutions for
, and has exactly two positive solutions for  (see Figure 2).
(see Figure 2).

Figure 2
Remark 3.10.
In fact, if we reverse the inequalities in (H1), (H1 ), (H2), we will obtain corresponding results similar to Theorems 3.8 and 3.9.
), (H2), we will obtain corresponding results similar to Theorems 3.8 and 3.9.
Also using the method in this paper, we can obtain the exact numbers of positive solutions for the Dirichlet problem

where  is a parameter. We assume that
is a parameter. We assume that
(H)  with
with  , and
, and  for all
for all .
.
Definition 3.11  .
.
Define

where  is the first eigenvalue of the corresponding linear problem of (3.19).
is the first eigenvalue of the corresponding linear problem of (3.19).
Theorem 3.12.
Let (H1 ), (H2), (H3), and (H4
), (H2), (H3), and (H4 ) hold. Then, the following are considered.
) hold. Then, the following are considered.
(i) All positive solutions of (3.19) lie on a single continuous curve  . And
. And  bifurcates from
bifurcates from  to the right to a unique degenerate positive solution
to the right to a unique degenerate positive solution  of (3.19), then it tends to the left to
of (3.19), then it tends to the left to  .
.
(ii) Equation (1.1) has no positive solution for  but has exactly one positive solution for
but has exactly one positive solution for  and has exactly two positive solutions for
and has exactly two positive solutions for  .
.
Theorem 3.13.
Let (H1), (H2), (H3), (H4 ) hold. Then
) hold. Then
(i) All positive solutions of (3.19) lie on two continuous curves  and
and  without intersection.
without intersection.  bifurcates from
bifurcates from  to infinity and
to infinity and  ;
;  bifurcates from
bifurcates from  to infinity and
to infinity and  . There is no degenerate positive solution on these curves. For any
. There is no degenerate positive solution on these curves. For any  ,
,  , and for any
, and for any  ,
,  .
.
(ii) Equation (3.19) has no positive solution for  , and has exactly one positive solution for
, and has exactly one positive solution for  , and has exactly two positive solutions for
, and has exactly two positive solutions for  .
.
Remark 3.14.
Theorems 3.12 and 3.13 extend the main result Theorem  in [10], where
in [10], where  for
for  .
.
4. Examples
In this section, we give some examples.
Example 4.1.
Let

Then,  satisfies (H1), (H2), and (H3). Moreover,
satisfies (H1), (H2), and (H3). Moreover,  ,
,  ,
,  , and
, and  .
.
Example 4.2.
Let

Then,  satisfies (H
satisfies (H ), (H2), and (H3). Moreover,
), (H2), and (H3). Moreover,  and
and  .
.
Example 4.3.
Let  . Here,
. Here,  ,
,  for all
for all , and
, and  is a large enough constant. Then,
is a large enough constant. Then,  satisfies (H4). On the other hand, functions which satisfy (H
satisfies (H4). On the other hand, functions which satisfy (H ) can be found easily.
) can be found easily.
References
Ambrosetti A, Hess P: Positive solutions of asymptotically linear elliptic eigenvalue problems. Journal of Mathematical Analysis and Applications 1980,73(2):411-422. 10.1016/0022-247X(80)90287-5
Asakawa H: Nonresonant singular two-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2001,44(6):791-809. 10.1016/S0362-546X(99)00308-9
Erbe LH, Wang H: On the existence of positive solutions of ordinary differential equations. Proceedings of the American Mathematical Society 1994,120(3):743-748. 10.1090/S0002-9939-1994-1204373-9
Ma R, Thompson B: Nodal solutions for nonlinear eigenvalue problems. Nonlinear Analysis: Theory, Methods & Applications 2004,59(5):707-718.
Ma R, Thompson B: Multiplicity results for second-order two-point boundary value problems with nonlinearities across several eigenvalues. Applied Mathematics Letters 2005,18(5):587-595. 10.1016/j.aml.2004.09.011
Korman P, Li Y, Ouyang T: An exact multiplicity result for a class of semilinear equations. Communications in Partial Differential Equations 1997,22(3-4):661-684. 10.1080/03605309708821278
Ouyang T, Shi J: Exact multiplicity of positive solutions for a class of semilinear problem. II. Journal of Differential Equations 1999,158(1):94-151. 10.1016/S0022-0396(99)80020-5
Ouyang T, Shi J: Exact multiplicity of positive solutions for a class of semilinear problems. Journal of Differential Equations 1998,146(1):121-156. 10.1006/jdeq.1998.3414
Shi J: Exact multiplicity of solutions to superlinear and sublinear problems. Nonlinear Analysis: Theory, Methods & Applications 2002,50(5):665-687. 10.1016/S0362-546X(01)00775-1
Korman P, Ouyang T: Exact multiplicity results for two classes of boundary value problems. Differential and Integral Equations 1993,6(6):1507-1517.
Korman P, Ouyang T: Solution curves for two classes of boundary-value problems. Nonlinear Analysis: Theory, Methods & Applications 1996,27(9):1031-1047. 10.1016/0362-546X(95)00108-8
Korman P: Uniqueness and exact multiplicity of solutions for a class of Dirichlet problems. Journal of Differential Equations 2008,244(10):2602-2613. 10.1016/j.jde.2008.02.014
Rynne B: Global bifurcation for 2mth order boundary value problems and infinitely many solutions of superlinear problems. Journal of Differential Equations 2003,188(2):461-472. 10.1016/S0022-0396(02)00146-8
Bari R, Rynne B: Solution curves and exact multiplicity results for 2mth order boundary value problems. Journal of Mathematical Analysis and Applications 2004,292(1):17-22. 10.1016/j.jmaa.2003.08.043
Korman P, Li Y: On the exactness of an S-shaped bifurcation curve. Proceedings of the American Mathematical Society 1999,127(4):1011-1020. 10.1090/S0002-9939-99-04928-X
Crandall MG, Rabinowitz PH: Bifurcation, perturbation of simple eigenvalues and linearized stability. Archive for Rational Mechanics and Analysis 1973, 52: 161-180.
Crandall MG, Rabinowitz PH: Bifurcation from simple eigenvalues. Journal of Functional Analysis 1971, 8: 321-340. 10.1016/0022-1236(71)90015-2
Rabinowitz PH: On bifurcation from infinity. Journal of Differential Equations 1973, 14: 462-475. 10.1016/0022-0396(73)90061-2
Acknowledgments
The authors are very grateful to the anonymous referees for their valuable suggestions. An is supported by SRFDP (no. 20060736001), YJ2009-16 A06/1020K096019, 11YZ225. Luo is supported by grant no. L09DJY065.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
An, Y., Luo, H. Exact Multiplicity of Positive Solutions for a Class of Second-Order Two-Point Boundary Problems with Weight Function. Bound Value Probl 2010, 207649 (2010). https://doi.org/10.1155/2010/207649
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/207649
 does not change its sign on
does not change its sign on 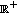 ; (ii)
; (ii)  changes its sign only once on
changes its sign only once on  .
. be such that
be such that 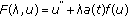 . We will show that the conditions of Theorem 1.3 hold.
. We will show that the conditions of Theorem 1.3 hold.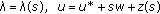 into (1.1), we obtain
into (1.1), we obtain 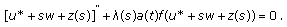
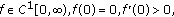 and (H4) hold. Suppose that
and (H4) hold. Suppose that 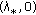 is a point where a bifurcation from the trivial solutions occurs and that
is a point where a bifurcation from the trivial solutions occurs and that  is the corresponding positive solution bifurcation curve of (1.1). If there exists
is the corresponding positive solution bifurcation curve of (1.1). If there exists  such that
such that 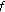 is superlinear (resp., sublinear) on
is superlinear (resp., sublinear) on 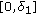 , then
, then  tends to the left (resp., the right) near
tends to the left (resp., the right) near  .
.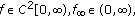 and (H4) hold. Suppose that
and (H4) hold. Suppose that  is a point where a bifurcation from infinity occurs and that
is a point where a bifurcation from infinity occurs and that  is the corresponding positive solution bifurcation curve of (1.1). If there exists
is the corresponding positive solution bifurcation curve of (1.1). If there exists 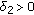 such that
such that  is superlinear (resp., sublinear) on
is superlinear (resp., sublinear) on 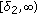 and
and 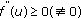 (resp.,
(resp., 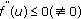 ) for
) for  , then
, then  tends to the right (resp., the left) near
tends to the right (resp., the left) near 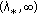 .
.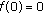 and
and 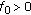 , then
, then  . From Lemma 3.5(i) and the standard Crandall and Rabinowitz theorem on local bifurcation from simple eigenvalues [
. From Lemma 3.5(i) and the standard Crandall and Rabinowitz theorem on local bifurcation from simple eigenvalues [ is the unique point where a bifurcation from the trivial solution occurs. Moreover, by Lemma 3.4, the curve bifurcates to the right. We denote this local curve by
is the unique point where a bifurcation from the trivial solution occurs. Moreover, by Lemma 3.4, the curve bifurcates to the right. We denote this local curve by 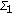 and continue
and continue 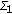 to the right as long as it is possible. Meanwhile, by Lemma 3.6, there is no positive solution of (1.1) which has the maximum value
to the right as long as it is possible. Meanwhile, by Lemma 3.6, there is no positive solution of (1.1) which has the maximum value  on
on 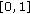 . So, if
. So, if 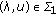 , then
, then 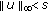 . From (1.1), we have
. From (1.1), we have