- Research Article
- Open access
- Published:
Slowly Oscillating Solutions of a Parabolic Inverse Problem: Boundary Value Problems
Boundary Value Problems volume 2010, Article number: 471491 (2010)
Abstract
The existence and uniqueness of a slowly oscillating solution to parabolic inverse problems for a type of boundary value problem are established. Stability of the solution is discussed.
1. Introduction
It is well known that the space  of almost periodic functions and some of its generalizations have many applications (e.g., [1–13] and references therein). However, little has been done for
of almost periodic functions and some of its generalizations have many applications (e.g., [1–13] and references therein). However, little has been done for  to inverse problems except for our work in [14–16]. Sarason in [17] studied the space
to inverse problems except for our work in [14–16]. Sarason in [17] studied the space  of slowly oscillating functions. This is a
of slowly oscillating functions. This is a  -subalgebra of
-subalgebra of  , the space of bounded, continuous, complex-valued functions
, the space of bounded, continuous, complex-valued functions  on
on  with the supremum norm
with the supremum norm  . Compared with
. Compared with  ,
,  is a quite large space (see [17–20]). What we are interested in
is a quite large space (see [17–20]). What we are interested in  is based on the belief that
is based on the belief that  certainly has a variety of applications in many mathematical areas too. In [15], we studied slowly oscillating solutions of a parabolic inverse problem for Cauchy problems. In this paper, we devote such solutions for a type of boundary value problem.
certainly has a variety of applications in many mathematical areas too. In [15], we studied slowly oscillating solutions of a parabolic inverse problem for Cauchy problems. In this paper, we devote such solutions for a type of boundary value problem.
Set  . Let
. Let  (resp.,
(resp.,  , where
, where  ) denote the
) denote the  -algebra of bounded continuous complex-valued functions on
-algebra of bounded continuous complex-valued functions on  (resp.,
(resp.,  ) with the supremum norm. For
) with the supremum norm. For  (resp.,
(resp.,  ) and
) and  , the translate of
, the translate of  by
by  is the function
is the function  (resp.,
(resp.,  ,
,  ).
).
Definition 1.1.
-
(1)
A function
 is called slowly oscillating if for every
is called slowly oscillating if for every  ,
,  , the space of the functions vanishing at infinity. Denote by
, the space of the functions vanishing at infinity. Denote by 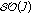 the set of all such functions.
the set of all such functions. -
(2)
A function
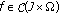 is said to be slowly oscillating in
is said to be slowly oscillating in  and uniform on compact subsets of
and uniform on compact subsets of  if
if  for each
for each  and is uniformly continuous on
and is uniformly continuous on 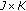 for any compact subset
for any compact subset 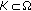 . Denote by
. Denote by 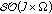 the set of all such functions. For convenience, such functions are also called uniformly slowly oscillating functions.
the set of all such functions. For convenience, such functions are also called uniformly slowly oscillating functions. -
(3)
Let
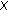 be a Banach space, and let
be a Banach space, and let  be the space of bounded continuous functions from
be the space of bounded continuous functions from 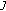 to
to  . If we replace
. If we replace  in (1) by
in (1) by 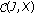 , then we get the definition of
, then we get the definition of  .
.
As in [17], we always assume that  is uniformly continuous.
is uniformly continuous.
The following two propositions come from [15, Section 1].
Proposition 1.2.
Let  be such that
be such that  is uniformly continuous on
is uniformly continuous on  . Then
. Then  .
.
For  , suppose that
, suppose that  for all
for all  . Define
. Define  by
by

The following proposition shows that the composite is also slowly oscillating.
Proposition 1.3.
Let  . If
. If  and
and  for all
for all  , then
, then  .
.
In the sequel, we will use the notations:  ,
,  .
.  means that
means that  is slowly oscillating in
is slowly oscillating in  and uniformly for
and uniformly for  ;
;  means that
means that  is slowly oscillating in
is slowly oscillating in  and uniformly on
and uniformly on  .
.
Let

be the fundamental solution of the heat equation [21].
2. A Type of Boundary Value Problem
We will keep the notation in Section 1 and at the same time introduce the following new notation:

In this section, we always assume the following:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ,
,  .
.
Let

be Green's function for the boundary value problems [22, 23].
The following estimates are easily obtained:

where  (
( ) are positive and increasing for
) are positive and increasing for  and
and  as
as  .
.
To show the main results of this section, the following lemmas are needed. The first lemma is Lemma 3.1 on page 15 in [24].
Lemma 2.1.
Let  ,
,  , and
, and  be real, continuous functions on
be real, continuous functions on  with
with  . If
. If

then

Lemma 2.2.
Let  be a continuous function on
be a continuous function on  . If
. If  ,
,  , and
, and  are nondecreasing and nonnegative on
are nondecreasing and nonnegative on  and
and

then

where

Proof.
Replacing  in the two integrals of (2.6) by the expression on the right hand side in (2.6), changing the integral order of the resulting inequality and making use of the monotonicity of
in the two integrals of (2.6) by the expression on the right hand side in (2.6), changing the integral order of the resulting inequality and making use of the monotonicity of  ,
,  and
and  , one gets
, one gets

Apply Lemma 2.1 to get the conclusion.
Lemma 2.3.
Let  ,
,  , and
, and  . Then the problem
. Then the problem

has a unique solution  , and
, and  is in
is in  and satisfies
and satisfies

where  .
.
One sees that  depends on
depends on  only and is bounded near zero.
only and is bounded near zero.
Proof.
The existence and uniqueness of the solution comes from Theorem 5.3 on page 320 in [25].
As in [22, 23], the solution  can be written as
can be written as

So,

By Lemma 2.1, one gets the desired inequality.
Now we show that  . As in the proofs of Lemmas 2.1 and 2.3 in [15], one gets
. As in the proofs of Lemmas 2.1 and 2.3 in [15], one gets  . For
. For  ,
,  with
with  ,
,

Note that

where  is a constant and
is a constant and

So,

By Lemma 2.1, one has

where  is a constant. Since
is a constant. Since  and
and  are slowly oscillating, the right-hand sides of the inequality above approaches zero as
are slowly oscillating, the right-hand sides of the inequality above approaches zero as  . This means that
. This means that  . The proof is complete.
. The proof is complete.
Consider the following problem.
Problem 1.
Find functions
 and
and
 such that
such that




One sees that


It follows from (2.24) that

Let  , and let
, and let  . We have the following two additional problems for
. We have the following two additional problems for  and
and  , respectively.
, respectively.
Problem 2.
Find functions
 and
and
 such that
such that




Problem 3.
Find functions
 and
and
 such that
such that




Lemma 2.4.
Problems 1, 2, and 3 are equivalent to each other.
Proof.
The existence and uniqueness of the solution  of Problem 2 can be easily obtained from that of the solution
of Problem 2 can be easily obtained from that of the solution  of Problem 1. Conversely, let (
of Problem 1. Conversely, let ( ) be the solution of Problem 2. We show that Problem 1 has a unique solution (
) be the solution of Problem 2. We show that Problem 1 has a unique solution ( ). The uniqueness comes from the uniqueness of (2.19)–(2.21). For the existence, let
). The uniqueness comes from the uniqueness of (2.19)–(2.21). For the existence, let

Obviously,  and satisfies (2.22). Also
and satisfies (2.22). Also  satisfies (2.21) because
satisfies (2.21) because  . By (2.23) and (2.27), one sees that (2.20) is true. Finally, we show that
. By (2.23) and (2.27), one sees that (2.20) is true. Finally, we show that  satisfies (2.19) and therefore, along with
satisfies (2.19) and therefore, along with  , constitutes a solution of Problem 1. In fact,
, constitutes a solution of Problem 1. In fact,

Thus, we have shown the equivalence of Problems 1 and 2. Replacing (2.34) by the function

the equivalence of Problems 2 and 3 can be proved similarly. The proof is complete.
By Lemma 2.4, to solve Problem 1, we only need to solve Problem 3. By (2.30)–(2.32), we have the integral equation about  :
:

Rewrite (2.33) as

where  is determined by (2.37).
is determined by (2.37).
One can directly test that Problem 3 is equivalent to (2.37)-(2.38).
Note that for a given  , Lemma 2.3 shows that (2.30)–(2.32) (or equivalently, (2.37)) have a unique solution
, Lemma 2.3 shows that (2.30)–(2.32) (or equivalently, (2.37)) have a unique solution  . Thus, (2.38) does define an operator
. Thus, (2.38) does define an operator  . Therefore, we only need to show that the integral (2.38) has a unique solution
. Therefore, we only need to show that the integral (2.38) has a unique solution  and
and  . That is,
. That is,  has a fixed point in
has a fixed point in  . Let
. Let

Set  , where
, where  . If
. If  , then, by Lemma 2.3,
, then, by Lemma 2.3,  is in
is in  , and so, by (2.38),
, and so, by (2.38),  is in
is in  with
with

Equation (2.37) gives the estimate

Choose  such that when
such that when  , one has
, one has  . It follows that
. It follows that

Choose  such that when
such that when  , one has
, one has

and therefore,  .
.
Let  ,
, . By (2.38),
. By (2.38),  . Note that the function
. Note that the function  is the solution of the problem
is the solution of the problem

So, by Lemma 2.3, one has

Choose  such that for
such that for  ,
,  . Now, set
. Now, set  . Then
. Then  is a contraction from
is a contraction from  into itself, and therefore, has a unique fixed point. Thus, we have shown.
into itself, and therefore, has a unique fixed point. Thus, we have shown.
Theorem 2.5.
Let functions  ,
,  ,
,  , and
, and  be as above. Then, for small
be as above. Then, for small  , Problem 3 has a unique solution (
, Problem 3 has a unique solution (  ) in
) in  with
with  and
and  .
.
Let  be the solutions of Problem 3 in
be the solutions of Problem 3 in  for the functions
for the functions  ,
,  ,
,  , and
, and  . Set
. Set  ,
,  ,
,  , and
, and  . For the stability of the solution, we have the following.
. For the stability of the solution, we have the following.
Theorem 2.6.
For  , one has
, one has

where  depends on
depends on  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Proof.
By (2.33),

So,

Note that the function  is the solution of the problem
is the solution of the problem

Using a formula similar to (2.37) and Lemma 2.2 for the function  , one gets
, one gets

Applying Lemma 2.2 and (2.48), one gets the desired conclusion with

where

and  is majorant of
is majorant of  . One can specially assume that
. One can specially assume that

The proof is complete.
Corollary 2.7.
Under the conditions in Theorem 2.6, the solution of Problem 3 is unique.
References
Agarwal RP, de Andrade B, Cuevas C: Weighted pseudo-almost periodic solutions of a class of semilinear fractional differential equations. Nonlinear Analysis: Real World Applications 2010,11(5):3532-3554. 10.1016/j.nonrwa.2010.01.002
Andres J, Bersani AM, Grande RF: Hierarchy of almost-periodic function spaces. Rendiconti di Matematica e delle sue Applicazioni 2006,26(2):121-188.
Basit B, Zhang C: New almost periodic type functions and solutions of differential equations. Canadian Journal of Mathematics 1996,48(6):1138-1153. 10.4153/CJM-1996-059-9
Berglund JF, Junghenn HD, Milnes P: Analysis on Semigroups: Function Spaces, Compactifications, Representations,, Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons, New York, NY, USA; 1989:xiv+334.
Bourgain J: Construction of approximative and almost periodic solutions of perturbed linear Schrödinger and wave equations. Geometric and Functional Analysis 1996,6(2):201-230. 10.1007/BF02247885
Corduneanu C: Almost Periodic Functions, Interscience Tracts in Pure and Applied Mathematics, no. 2. 1st edition. John Wiley & Sons, New York, NY, USA; 1968:x+237.
Corduneanu C: Almost Periodic Functions. 2nd edition. John Wiley & Sons, New York, NY, USA; 1989.
Diagan T: Pseudo Almost Periodic Functions in Banach spaces. Nova Science, New York, NY, USA; 2007.
Fink AM: Almost Periodic Differential Equations, Lecture Notes in Mathematics. Volume 377. Springer, Berlin, Germany; 1974:viii+336.
Hino Y, Naito T, Nguyen Van Minh , Shin JS: Almost Periodic Solutions of Differential Equations in Banach Spaces, Stability and Control: Theory, Methods and Applications. Volume 15. Taylor & Francis, London, UK; 2002:viii+250.
N'Guérékata GM: Topics in Almost Automorphy. Springer, New York, NY, USA; 2005:xii+168.
Shen W: Travelling waves in time almost periodic structures governed by bistable nonlinearities. I. Stability and uniqueness. Journal of Differential Equations 1999,159(1):1-54. 10.1006/jdeq.1999.3651
Zhang C: Almost Periodic Type Functions and Ergodicity. Science Press, Beijing, China; Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:xii+355.
Zhang C, Yang F: Remotely almost periodic solutions of parabolic inverse problems. Nonlinear Analysis: Theory, Methods & Applications 2006,65(8):1613-1623. 10.1016/j.na.2005.10.036
Yang F, Zhang C: Slowly oscillating solutions of parabolic inverse problems. Journal of Mathematical Analysis and Applications 2007,335(2):1238-1258. 10.1016/j.jmaa.2007.01.098
Zhang C, Yang F: Pseudo almost periodic solutions to parabolic boundary value inverse problems. Science in China. Series A 2008,51(7):1203-1214. 10.1007/s11425-008-0006-2
Sarason D: Remotely almost periodic functions. In Proceedings of the Conference on Banach Algebras and Several Complex Variables (New Haven, Conn., 1983), Providence, RI, USA, Contemp. Math.. Volume 32. American Mathematical Society; 1984:237-242.
Zhang C: New limit power function spaces. IEEE Transactions on Automatic Control 2004,49(5):763-766. 10.1109/TAC.2004.825970
Zhang C, Meng C:
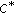 -algebra of strong limit power functions. IEEE Transactions on Automatic Control 2006,51(5):828-831. 10.1109/TAC.2006.875016
-algebra of strong limit power functions. IEEE Transactions on Automatic Control 2006,51(5):828-831. 10.1109/TAC.2006.875016Zhang C: Strong limit power functions. The Journal of Fourier Analysis and Applications 2006,12(3):291-307. 10.1007/s00041-006-6004-2
Friedman A: Partial Differential Equations of Parabolic Type. Prentice-Hall, Englewood Cliffs, NJ, USA; 1964:xiv+347.
Guo B: Inverse Problem of Parabolic Partial Differential Equations. Science and Technology Press of Heilongjiang Province, Harbin, China; 1988.
Zauderer E: Partial Differential Equations of Applied Mathematics, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1983:xiii+779.
Hale JK, Verduyn Lunel SM: Introduction to Functional-Differential Equations, Applied Mathematical Sciences. Volume 99. Springer, New York, NY, USA; 1993:x+447.
Ladyzenskaja OA, Solonnikov VA, Ural'ceva NN: Linear and Quasi-Linear Equations of Parabolic Type. American Mathematical Society, Providence, RI, USA; 1968.
Acknowledgment
The research is supported by the NSF of China (no. 11071048).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, F., Zhang, C. Slowly Oscillating Solutions of a Parabolic Inverse Problem: Boundary Value Problems. Bound Value Probl 2010, 471491 (2010). https://doi.org/10.1155/2010/471491
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/471491
 is called slowly oscillating if for every
is called slowly oscillating if for every  ,
,  , the space of the functions vanishing at infinity. Denote by
, the space of the functions vanishing at infinity. Denote by 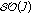 the set of all such functions.
the set of all such functions.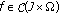 is said to be slowly oscillating in
is said to be slowly oscillating in  and uniform on compact subsets of
and uniform on compact subsets of  if
if  for each
for each  and is uniformly continuous on
and is uniformly continuous on 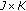 for any compact subset
for any compact subset 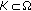 . Denote by
. Denote by 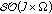 the set of all such functions. For convenience, such functions are also called uniformly slowly oscillating functions.
the set of all such functions. For convenience, such functions are also called uniformly slowly oscillating functions.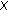 be a Banach space, and let
be a Banach space, and let  be the space of bounded continuous functions from
be the space of bounded continuous functions from 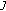 to
to  . If we replace
. If we replace  in (1) by
in (1) by 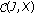 , then we get the definition of
, then we get the definition of  .
. -algebra of strong limit power functions. IEEE Transactions on Automatic Control 2006,51(5):828-831. 10.1109/TAC.2006.875016
-algebra of strong limit power functions. IEEE Transactions on Automatic Control 2006,51(5):828-831. 10.1109/TAC.2006.875016