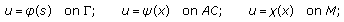The Jump Problem for Mixed-Type Equations with Defects on the Type Change Line

Abstract

The jump problem and problems with defects on the type change line for model mixed-type equations in the mixed domains are investigated. The explicit solutions of the jump problem are obtained by the method of integral equations and by the Fourier transformation method. The problems with defects are reduced to singular integral equations. Some results for the solution of the equation under consideration are discussed concerning the existence and uniqueness for the solution of the suggested problem.

1. Introduction

Consider the jump problem and problems with defects on the type change line for the mixed-type equation of the first kind

(1.1)

This equation is a model equation among mixed-type equations of the first kind. For and , (1.1) coincides with Lavrent'ev-Bitsadze equation and the Tricomi equation, respectively. For even (1.1) coincides with the Gellerstedt equation (see, [1–9]). Equation (1.1) is elliptic for and hyperbolic for . In the formulation of the boundary value problems in the mixed domain, it is usually required that the unknown solution and its normal derivative should be continuous on the type change line , that is, the conditions

(1.2)

should be fulfilled. More generally conjugation conditions with continuous coefficients of the form

(1.3)

have been discussed (see [10, 11]). There are defects on the type change line if the conjugation conditions (1.2) are replaced by conditions of another form. For example, if the boundary values of the solution or its normal derivative are given on defect. Such terminology is taken from the boundary value problems of elasticity theory. So problems with defects on the type change line will form special class of boundary value problems for the mixed-type equations with discontinuous coefficients in the conjugation conditions. We say that boundary value problems in the mixed domain with the conjugation conditions

(1.4)

are the jump problems on the type change line for (1.1). Obviously, the classical Tricomi problem is the jump problem with zero jump. Two methods are used in this papre to solve the jump problem: the method of integral equations and the method of integral Fourier transformation. It is shown that explicit solutions of the jump problem can be used as potentials under researching boundary value problems with defects.

2. The Jump Problem for Lavrent'ev-Bitsadze Equation: The Method of Integral Equations

Let the domain be bounded by the line with the ends at the points and of the real axis and by the characteristics and of Lavrent'ev-Bitsadze equation

(2.1)

Let and be the elliptic and the hyperbolic parts of the mixed domain .

The unknown solution of (2.1) in the jump problem as in the Tricomi problem should satisfy the following boundary conditions:

(2.2)

(here is arc abscissa of arc being measured from the point to the point ).

As it is commonly accepted in the theory of the boundary value problems for the mixed-type equations we denote

(2.3)

Assume that on the segment there is the finite number of points in which functions can have discontinuities of the first kind and functions can have singularities of integrable order. We say that such points are the exclusive points.

Denote by is the set of points of the segment which are not the exclusive ones.

We can seek a solution of the problem in the different classes of solutions [2, Section ]. The regular solution and satisfies (2.1) in . The generalized solution of the class belongs to , satisfies (2.1) in and is the generalized solution of (2.1) in in the sense that

(2.4)

(the D'Alembert formula) where . Here is a class of functions which can have singularities of integrable order at the points and , but satisfy Hoelder's condition with some index at any part of the interval . As it is known the generalized solution of the class will be regular if we assume in addition that .

In the jump problem on the type change line for Lavrent'ev-Bitsadze equation, we need to seek a function which

(1)is regular or generalized solution of (2.1) in ;

(2)satisfies the boundary conditions (2.2);

(3)has the limiting values on and

(4)the conditions

(2.5)

are fulfilled.

Let us obtain functional correlations at the segment which connect functions , and . The general scheme of reasoning is just the same as under solving the Tricomi problem.

Consider auxilliary boundary value problem in the domain . Let be the Green function of the problem for (2.1) in the domain . Then in

(2.6)

By this

(2.7)

(2.8)

From D'Alembert's formula (2.4) and condition on the characteristic it follows immediately that

(2.9)

Consider system of (2.7), (2.9), and (2.5) for functions . Subtracting (2.9) from (2.7) we get

(2.10)

It follows from here that function should be a solution of integral equation

(2.11)

(2.12)

Similar equation can be obtained for the function .

If the domain is a semidisc , then

(2.13)

(2.14)

Let us transform the integral equation (2.11) with logarithmic singularity in the kernel into the integral equation with the analogue of the Cauchy kernel. As

(2.15)

so the new function to be found,

(2.16)

should satisfy the equation

(2.17)

Generally speaking (2.17) is the complete singular integral equation with the Cauchy kernel, but special form of the kernel enables us to construct its solution in the explicit form. By this it is advisible to use the method of reduction to the Riemann boundary value problem for automorphic functions [12, Chapter III]. Consider an auxiliary piecewise-holomorphic function

(2.18)

satisfying the automorphic type condition

(2.19)

It follows from the analogues of the Sohotski formulas that integral equation (2.17) is equivalent to the Riemann boundary value problem

(2.20)

for analytic functions satisfying the condition (2.19). The solutions of problem (2.20) should be limited at the points and at infinity.

The canonical function of the Riemann problem in class of the automorphic functions has the form

(2.21)

where

(2.22)

is simple automorphic function of group . As it is shown in [13, page 111], there is a unique opportunity to choose numbers ( being stationary points of group of the homographic transformations).

So index of problem (2.20) and its unique solution limited at infinity

(2.23)

By condition (2.19) an arbitrary constant in the right-hand side is equal to zero. Since the boundary value of the canonical function from the upper half-plane on

(2.24)

then

(2.25)

By this if the elliptic part of the mixed domain is a semidisc then by formula (2.25), we can write down the solution of the integral equation (2.11) in the form

(2.26)

The function to be found can be obtained by differentiation, but as it will be shown later it is not obligatory.

By the main correlation (2.7)

(2.27)

here it is taken into account that function satisfies (2.17). Expressions of functions can be obtained from conditions (2.5).

The solution of the jump problem in the domain can be easily derived by the D'Alembert formula (2.4), and it is not necessary to seek the expression of the function for this, it is sufficient to have formula to calculate its primitive. The solution of the jump problem in the domain can be obtained by two methods: either as a solution of problem or as a solution of the Dirichlet problem.

Let be a simple connected domain bounded by piecewise-smooth curve and let function conformally map by variable in onto unit disc in such way that . Then (see, [14, page 464]) function

(2.28)

is the Green function of the Dirichlet problem for the domain . If is conformal mapping of the domain onto unit disc then

(2.29)

More general statement is formulated in [2, page 30]. If the function maps the domain of the plane onto the domain of the plane and is the Green function of the Dirichlet problem for the domain , then is the Green function of the Dirichlet problem for the domain .

In the case of problem it is also possible to use the method of conformal mappings [2, Section ]. Let domains and be bounded by segment of real axis and by curves and placed in the upper half-plane. Let function map the domain onto the domain in such way that goes over into and ends of this segment remain stationary. If is the Green function of problem for the domain , then is the Green function of problem for the domain .

By this way, the Green function of problem for the domain in the jump problem can be derived from the Green function of problem for some simple canonical domain by conformal mapping. In [2] the upper half-plane is chosen as a canonical domain but in our case a semidisc is more convenient to be considered as such domain. Hence if is the Green function (2.13) of the problem for semidisc and is a mapping of any other domain onto this semidisc satisfying the above mentioned conditions. Then for the Green function of the problem for the domain , we have

(2.30)

So the integral equation (2.11) can be transformed into equation of the form (2.17) by substitution of variables.

3. The Jump Problem for Lavrent'ev-Bitsadze Equation: The Method of Fourier Transformation

Let us construct the solution of the jump problem for Lavrent'ev-Bitsadze equation in the unbounded mixed domain by the method of the integral Fourier transformation.

Preliminary, we consider two auxiliary Cauchy problems in the upper and lower half-planes using some results of the works [15, 16]. We will use the following denotions: under Fourier transformation function goes over into function (distribution) .

Note that the boundary value problems in the half-space for partial differential equations have been investigated quite adequately (see, [17]). If the Cauchy problem in the half-space is overdetermined, then analysis of the algebraic equation for the Fourier transform of the unknown solution gives necessary and sufficient conditions for the boundary functions.

We seek a solution of (2.1) in the upper half-plane satisfying the boundary conditions

(3.1)

The Fourier transform of the unknown solution will be a solution of the equation

(3.2)

This solution exists if and only if when the right-hand side of (3.2) vanishes under , that is, the condition

(3.3)

is fulfilled. Consequently,

(3.4)

or

(3.5)

Equality (3.3) is the main correlation between boundary functions and .

We seek a solution of (2.1) in the lower half-plane satisfying the boundary conditions

(3.6)

The Fourier transform of the unknown solution satisfies the equation

(3.7)

and boundary functions can be given arbitrary.

It follows from (3.7), that

(3.8)

(this distribution is obtained by the method of passing to the complex plane). So

(3.9)

Note that, if we pass in this formula from the Fourier transforms of the boundary functions to their prototypes we obtain the D'Alembert formula (2.4).

Consider the jump problem for Lavrent'ev-Bitsadze equation in the unbounded mixed domain. Let be the upper half-plane, be the unbounded characteristic triangle bounded by and by positive semiaxis of the axis . We should seek a solution of (2.1) under which satisfying the boundary conditions on the negative semiaxis

(3.10)

on the characteristic

(3.11)

and on the line of type change under

(3.12)

In the particular case under , the jump problem coincides with the Tricomi problem in the unbounded mixed domain. Without loss of generality we can assume that .

We will seek a solution of the jump problem in the upper and in the lower half-planes as solutions of the Cauchy problems. Let us continue the unknown solution in onto the whole lower half-plane so that

(3.13)

The Fourier transforms of values of the unknown solution on the axis should satisfy the transformed conditions (3.12)

(3.14)

and the condition (3.3). Here are the Fourier transforms of functions being completed by zero up to the whole axis.

Denote by , and represent each of these functions as a sum of the Fourier transforms of one-side-functions. Hence

(3.15)

By condition (3.10),

(3.16)

where is the Fourier transform of the boundary function being completed by zero up to the whole axis.

Condition (3.11) on the characteristic can be written down in the form

(3.17)

where is the Fourier transform of the boundary function being completed by zero up to the whole axis. Actually, by the D'Alembert formula

(3.18)

After Fourier transformation subject to the evident identity

(3.19)

we obtain (3.17).

Condition (3.3) in the new denotions has the form

(3.20)

Excluding function from (3.17) and (3.20) we get in view of (3.16)

(3.21)

Equality (3.21) is the condition of the Riemann boundary value problem with discontinuous coefficient given on the real axis (this equality is being understood as the equality of distributions).

Note that solution of the jump problem in the whole plane without condition on the characteristic (3.11) is not unique but is determined within the arbitrary function.

The canonical function has the form

(3.22)

where is a single-valued branch of the power function which is chosen in the plane with a cut along positive semiaxis of real axis and takes on the real values on the upper side of the cut.

Denote by

(3.23)

Then

(3.24)

By the Sohotski formulas

(3.25)

Now we can easily obtain the expressions of the other auxiliary functions and consequently, the solution of the jump problem in the domains and .

The technique of the integral Fourier transformation can be used also in the cases when the mixed domain in the jump problem has another form.

If the elliptic part of the mixed domain is, for example, a semidisc then the Fourier transformation method can be modificated in the following way. Assume that the unknown solution of the jump problem on the semidisc is equal to zero. Continue the function to the whole upper half-plane symmetrically about , that is, in such way that values of function are equal at the points symmetrical about semidisc. Besides the solution and its normal derivative should be continuous on the semidisc. Then all formulas obtained at the beginning of the section remain valid but after substitution of variable integrals on infinite intervals can be transformed into integrals on segment. This method can be used in more general case when the elliptic part of the mixed domain is a half of the symmetrical about real axis fundamental domain of group of homographic transformations [12, Chapter III].

4. The Boundary Value Problems with Defect on the Line of Type Change for Lavrent'ev-Bitsadze Equation

Let the mixed domain be bounded by the line with the ends at the points and of the real axis and by characteristics and of Lavrent'ev-Bitsadze equation (2.1). Let be a set of disjoint segments placed inside the segment and let be a complement of with respect to .

We should seek the function with the following properties:

(1) satisfies (2.1) in under (classical or generalized solution);

(2);

• (3)
  

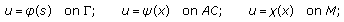  (4.1)

(4) satisfies on the conjugation condition (1.4).

If the set is empty and (there are no defects), then the problem under consideration coincides with the classical Tricomi problem. If , then we have two independent boundary value problems: the Dirichlet problem for the Laplace equation in and the Goursat problem in .

Later on for simplicity we will assume that in the set there is only one segment and .

If in the problem with defect the values of the unknown solution are given on the type change line, then we say that such defect is the defect of the first kind. If on the values of the derivative of the unknown solution are given (the defect of the 2nd kind), then by the main correlation (2.9) nothing changes in fact. By the same reason the problem with defect of the 3d kind (when on the linear combination of the solution and its derivative are given) can be reduced to the problem with defect of the 1st kind. Note that defect can be considered as a cut and independent boundary conditions can be given on every side of the cut.

We will seek a solution of the problem with defect on the line of type change as a solution of the jump problem (see Section 1). Let the elliptic part of the mixed domain be a semidisc. Without loss of generality we can assume that .

It follows from the boundary conditions on the type change line that almost everywhere on (except for only points and probably) and on and on . In the interval function is still unknown in the meantime. This function can be found from the boundary condition

(4.2)

By formula (2.27)

(4.3)

Since outside interval the function should satisfy the integral equation

(4.4)

The integral equation (4.4) is the integral equation with logarithmic kernel represented in the form of the integral with the analogue of the Cauchy kernel with variable limit. Introduce new unknown function

(4.5)

Then (4.4) can be transformed into the integral equation with the analogue of the Cauchy kernel

(4.6)

by this under and under , where

(4.7)

is supplementary unknown constant.

Let us construct the explicit solution of the integral equation (4.6). Denote by

(4.8)

Then

(4.9)

where

(4.10)

By the auxiliary function

(4.11)

pass to the Riemann boundary value problem with condition

(4.12)

solutions of which we should seek in the class of functions bounded at the points and . Since the index of the problem its solution exists if and only if when the solvability condition

(4.13)

is fulfilled. From the equality (4.13) the constant will be determined and so the Riemann problem (4.12) will have the unique solution.

Further operations are evident. The difference of the limiting values of the solution of the Riemann problem gives the unknown function on , by this the function will be determined and the function if it is necessary. But as it was mentioned above, it is sufficient to have only the expression of primitive of the function but not of this function itself.

If the mixed domain is unbounded it is convenient to use under solving the problem with defect on the type change line the results of Section 2 obtained by the Fourier transformation method. Depending on the kind of defect one of the auxiliary functions and will be identically equal to zero and the values of another function on the defect will remain unknown. Immediately from the formula (4.4) it is easy to get the integral equation equivalent to the problem with defect.