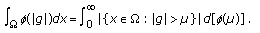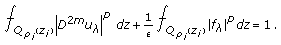- Research Article
- Open access
- Published:
Global Optimal Regularity for the Parabolic Polyharmonic Equations
Boundary Value Problems volume 2010, Article number: 879821 (2010)
Abstract
We show the global regularity estimates for the following parabolic polyharmonic equation  in
in  under proper conditions. Moreover, it will be verified that these conditions are necessary for the simplest heat equation
under proper conditions. Moreover, it will be verified that these conditions are necessary for the simplest heat equation  in
in  .
.
1. Introduction
Regularity theory in PDE plays an important role in the development of second-order elliptic and parabolic equations. Classical regularity estimates for elliptic and parabolic equations consist of Schauder estimates,  estimates, De Giorgi-Nash estimates, Krylov-Safonov estimates, and so on.
estimates, De Giorgi-Nash estimates, Krylov-Safonov estimates, and so on.  and Schauder estimates, which play important roles in the theory of partial differential equations, are two fundamental estimates for elliptic and parabolic equations and the basis for the existence, uniqueness, and regularity of solutions.
and Schauder estimates, which play important roles in the theory of partial differential equations, are two fundamental estimates for elliptic and parabolic equations and the basis for the existence, uniqueness, and regularity of solutions.
The objective of this paper is to investigate the generalization of  estimates, that is, regularity estimates in Orlicz spaces, for the following parabolic polyharmonic problems:
estimates, that is, regularity estimates in Orlicz spaces, for the following parabolic polyharmonic problems:


where  ,
,  and
and  is a positive integer. Since the 1960s, the need to use wider spaces of functions than Sobolev spaces arose out of various practical problems. Orlicz spaces have been studied as the generalization of Sobolev spaces since they were introduced by Orlicz [1] (see [2–6]). The theory of Orlicz spaces plays a crucial role in many fields of mathematics (see [7]).
is a positive integer. Since the 1960s, the need to use wider spaces of functions than Sobolev spaces arose out of various practical problems. Orlicz spaces have been studied as the generalization of Sobolev spaces since they were introduced by Orlicz [1] (see [2–6]). The theory of Orlicz spaces plays a crucial role in many fields of mathematics (see [7]).
We denote the distance in  as
as

and the cylinders in  as
as

where  is an open ball in
is an open ball in  . Moreover, we denote
. Moreover, we denote

where  is a multiple index,
is a multiple index,  . For convenience, we often omit the subscript
. For convenience, we often omit the subscript  in
in  and write
and write  .
.
Indeed if  , then (1.1) is simplified to be the simplest heat equation.
, then (1.1) is simplified to be the simplest heat equation.  estimates and Schauder estimates for linear second-order equations are well known (see [8, 9]). When
estimates and Schauder estimates for linear second-order equations are well known (see [8, 9]). When  , the corresponding regularity results for the higher-order parabolic equations are less. Solonnikov [10] studied
, the corresponding regularity results for the higher-order parabolic equations are less. Solonnikov [10] studied  and Schauder estimates for the general linear higher-order parabolic equations with the help of fundamental solutions and Green functions. Moreover, in [11] we proved global Schauder estimates for the initial-value parabolic polyharmonic problem using the uniform approach as the second-order case. Recently we [6] generalized the local
and Schauder estimates for the general linear higher-order parabolic equations with the help of fundamental solutions and Green functions. Moreover, in [11] we proved global Schauder estimates for the initial-value parabolic polyharmonic problem using the uniform approach as the second-order case. Recently we [6] generalized the local  estimates to the Orlicz space
estimates to the Orlicz space

for

where  (see Definition 1.2) and
(see Definition 1.2) and  is an open bounded domain in
is an open bounded domain in  . When
. When  with
with  , (1.6) is reduced to the local
, (1.6) is reduced to the local  estimates. In fact, we can replace
estimates. In fact, we can replace  of
of  in (1.6) by the power of
in (1.6) by the power of  for any
for any  .
.
Our purpose in this paper is to extend local regularity estimate ( ) in [6] to global regularity estimates, assuming that
) in [6] to global regularity estimates, assuming that  . Moreover, we will also show that the
. Moreover, we will also show that the  condition is necessary for the simplest heat equation
condition is necessary for the simplest heat equation  in
in  . In particular, we are interested in the estimate like
. In particular, we are interested in the estimate like

where  is a constant independent from
is a constant independent from  and
and  . Indeed, if
. Indeed, if  with
with  , (1.8) is reduced to classical
, (1.8) is reduced to classical  estimates. We remark that although we use similar functional framework and iteration-covering procedure as in [6, 12], more complicated analysis should be carefully carried out with a proper dilation of the unbounded domain.
estimates. We remark that although we use similar functional framework and iteration-covering procedure as in [6, 12], more complicated analysis should be carefully carried out with a proper dilation of the unbounded domain.
Here for the reader's convenience, we will give some definitions on the general Orlicz spaces.
Definition 1.1.
A convex function  is said to be a Young function if
is said to be a Young function if

Definition 1.2.
A Young function  is said to satisfy the global
is said to satisfy the global  condition, denoted by
condition, denoted by  , if there exists a positive constant
, if there exists a positive constant  such that for every
such that for every  ,
,

Moreover, a Young function  is said to satisfy the global
is said to satisfy the global  condition, denoted by
condition, denoted by  , if there exists a number
, if there exists a number  such that for every
such that for every  ,
,

Example 1.3.
-
(i)
 , but
, but  .
. -
(ii)
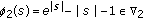 , but
, but 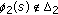 .
. -
(iii)
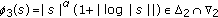 ,
,  .
.
Remark 1.4.
If a function  satisfies (1.10) and (1.11), then
satisfies (1.10) and (1.11), then

for every  and
and  , where
, where  and
and  .
.
Remark 1.5.
Under condition (1.12), it is easy to check that  satisfies
satisfies

Definition 1.6.
Assume that  is a Young function. Then the Orlicz class
is a Young function. Then the Orlicz class  is the set of all measurable functions
is the set of all measurable functions  satisfying
satisfying

The Orlicz space  is the linear hull of
is the linear hull of  .
.
Lemma 1.7 (see [2]).
Assume that  and
and  . Then
. Then
(1) ,
,
(2) is dense in
is dense in  ,
,
-
(3)
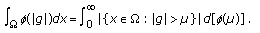 (1.15)
(1.15)
Now let us state the main results of this work.
Theorem 1.8.
Assume that  is a Young function and
is a Young function and  satisfies
satisfies

Then if the following inequality holds

One has

Theorem 1.9.
Assume that  . If
. If  is the solution of (1.1)-(1.2) with
is the solution of (1.1)-(1.2) with  , then (1.8) holds.
, then (1.8) holds.
Remark 1.10.
We would like to point out that the  condition is necessary. In fact, if the local
condition is necessary. In fact, if the local  estimate (1.6)
estimate (1.6)  is true, then by choosing
is true, then by choosing

we have

which implies that

2. Proof of Theorem 1.8
In this section we show that  satisfies the global
satisfies the global  condition if
condition if  satisfies (1.16) and estimate (1.17) is true.
satisfies (1.16) and estimate (1.17) is true.
Proof.
Now we consider the special case in (1.16) when

for any constant  , where
, where  and
and  is a cutoff function satisfying
is a cutoff function satisfying

Therefore the problem (1.16) has the solution

It follows from (1.17), (2.1), and (2.2) that

We know from (2.3) that

Define

Then when  and
and  , we have
, we have

since

Therefore, since  for
for  and
and  , we conclude that
, we conclude that

Recalling estimate (2.4) we find that

which implies that

By changing variable we conclude that, for any  ,
,

where  . Let
. Let  and
and  . Then we conclude from (2.12) that
. Then we conclude from (2.12) that

Now we use (2.12) and (2.13) to obtain that

where we choose that  ,
,  in (2.13). Set
in (2.13). Set  . Then we have
. Then we have

when  is chosen large enough. This implies that
is chosen large enough. This implies that  satisfies the
satisfies the  condition. Thus this completes our proof.
condition. Thus this completes our proof.
3. Proof of the Main Result
In this section, we will finish the proof of the main result, Theorem 1.9. Just as [6], we will use the following two lemmas. The first lemma is the following integral inequality.
Lemma 3.1 (see [6]).
Let  ,
,  and
and  , where
, where  is defined in (1.12). Then for any
is defined in (1.12). Then for any  one has
one has

Moreover, we recall the following result.
Lemma 3.2 (see [10, Theorem  ]).
]).
Assume that  for
for  . There exists a unique solution
. There exists a unique solution  of (1.1)-(1.2) with the estimate
of (1.1)-(1.2) with the estimate

Moreover, we give one important lemma, which is motivated by the iteration-covering procedure in [12]. To start with, let  be a solution of (1.1)-(1.2). Let
be a solution of (1.1)-(1.2). Let

In fact, in the subsequent proof we can choose any constant  with
with  . Now we write
. Now we write

while  is a small enough constant which will be determined later. Set
is a small enough constant which will be determined later. Set

for any  . Then
. Then  is still the solution of (1.1)-(1.2) with
is still the solution of (1.1)-(1.2) with  replacing
replacing  . Moreover, we write
. Moreover, we write

for any domain  in
in  and the level set
and the level set

Next, we will decompose the level set  .
.
Lemma 3.3.
For any  , there exists a family of disjoint cylinders
, there exists a family of disjoint cylinders  with
with  and
and  such that
such that


where  . Moreover, one has
. Moreover, one has

Proof.
( ) Fix any
) Fix any  . We first claim that
. We first claim that

where  satisfies
satisfies  . To prove this, fix any
. To prove this, fix any  and
and  . Then it follows from (3.4) that
. Then it follows from (3.4) that

( ) For a.e.
) For a.e.  , from Lebesgue's differentiation theorem we have
, from Lebesgue's differentiation theorem we have

which implies that there exists some  satisfying
satisfying

Therefore from (3.11) we can select a radius  such that
such that

Therefore, applying Vitali's covering lemma, we can find a family of disjoint cylinders  such that (3.8) and (3.9) hold.
such that (3.8) and (3.9) hold.
-
(3)
Equation (3.8) implies that
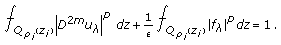 (3.16)
(3.16)
Therefore, by splitting the two integrals above as follows we have

Thus we can obtain the desired result (3.10).
Now we are ready to prove the main result, Theorem 1.9.
Proof.
In the following by the elementary approximation argument as [3, 12] it is sufficient to consider the proof of (1.8) under the additional assumption that  . In view of Lemma 3.3, given any
. In view of Lemma 3.3, given any  , we can construct a family of cylinders
, we can construct a family of cylinders  , where
, where  . Fix
. Fix  . It follows from (3.6) and (3.8) in Lemma 3.3 that
. It follows from (3.6) and (3.8) in Lemma 3.3 that

We first extend  from
from  to
to  by the zero extension and denote by
by the zero extension and denote by  . From Lemma 3.2, there exists a unique solution
. From Lemma 3.2, there exists a unique solution  of
of

with the estimate

Therefore we see that

Set  . Then we know that
. Then we know that

Moreover, by (3.18) and (3.21) we have

Thus from the elementary interior  regularity, we know that there exists a constant
regularity, we know that there exists a constant  such that
such that

Set  . Therefore, we deduce from (3.5) and (3.24) that
. Therefore, we deduce from (3.5) and (3.24) that

Then according to (3.18) and (3.21), we discover

Therefore, from (3.10) in Lemma 3.3 we find that

where  . Recalling the fact that the cylinders
. Recalling the fact that the cylinders  are disjoint,
are disjoint,

and then summing up on  in the inequality above, we have
in the inequality above, we have

Therefore, from Lemma 1.7(3) and the inequality above we have

Consequently, from Lemma 3.1 we conclude that

where  and
and  . Finally selecting a suitable
. Finally selecting a suitable  such that
such that  , we finish the proof.
, we finish the proof.
References
Orlicz W: Über eine gewisse Klasse von Räumen vom Typus B. Bulletin International de l'Académie Polonaise Série A 1932, 8: 207-220.
Adams RA, Fournier JJF: Sobolev Spaces. Volume 140. 2nd edition. Academic Press, Amsterdam, The Netherlands; 2003:xiv+305.
Byun S, Yao F, Zhou S: Gradient estimates in Orlicz space for nonlinear elliptic equations. Journal of Functional Analysis 2008,255(8):1851-1873.
Jia H, Li D, Wang L: Regularity of Orlicz spaces for the Poisson equation. Manuscripta Mathematica 2007,122(3):265-275. 10.1007/s00229-006-0066-y
Kokilashvili V, Krbec M: Weighted inequalities in Lorentz and Orlicz spaces. World Scientific, River Edge, NJ, USA; 1991:xii+233.
Yao F: Regularity theory in Orlicz spaces for the parabolic polyharmonic equations. Archiv der Mathematik 2008,90(5):429-439. 10.1007/s00013-008-2576-1
Rao MM, Ren ZD: Applications of Orlicz Spaces, Monographs and Textbooks in Pure and Applied Mathematics. Volume 250. Marcel Dekker, New York, NY, USA; 2002:xii+464.
Gilbarg D, Trudinger N: Elliptic Partial Differential Equations of Second Order. 3rd edition. Springer, Berlin, Germany; 1998.
Lieberman GM: Second Order Parabolic Differential Equations. World Scientific, River Edge, NJ, USA; 1996:xii+439.
Solonnikov VA: On boundary value problems for linear parabolic systems of differential equations of general form. Trudy Matematicheskogo Instituta Imeni V. A. Steklova 1965, 83: 3-163.
Yao F-P, Zhou S-L: Schauder estimates for parabolic equation of bi-harmonic type. Applied Mathematics and Mechanics 2007,28(11):1503-1516. 10.1007/s10483-007-1110-z
Acerbi E, Mingione G: Gradient estimates for a class of parabolic systems. Duke Mathematical Journal 2007,136(2):285-320. 10.1215/S0012-7094-07-13623-8
Acknowledgments
The author wishes to thank the anonymous referee for offering valuable suggestions to improve the expressions. This work is supported in part by Tianyuan Foundation (10926084) and Research Fund for the Doctoral Program of Higher Education of China (20093108120003). Moreover, the author wishes to thank the department of mathematics at Shanghai university which was supported by the Shanghai Leading Academic Discipline Project (J50101) and Key Disciplines of Shanghai Municipality (S30104).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yao, F. Global Optimal Regularity for the Parabolic Polyharmonic Equations. Bound Value Probl 2010, 879821 (2010). https://doi.org/10.1155/2010/879821
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/879821
 , but
, but  .
.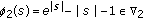 , but
, but 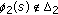 .
.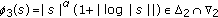 ,
,  .
.