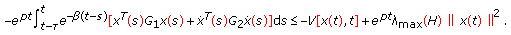- Research Article
- Open access
- Published:
Exponential Stability and Estimation of Solutions of Linear Differential Systems of Neutral Type with Constant Coefficients
Boundary Value Problems volume 2010, Article number: 956121 (2010)
Abstract
This paper investigates the exponential-type stability of linear neutral delay differential systems with constant coefficients using Lyapunov-Krasovskii type functionals, more general than those reported in the literature. Delay-dependent conditions sufficient for the stability are formulated in terms of positivity of auxiliary matrices. The approach developed is used to characterize the decay of solutions (by inequalities for the norm of an arbitrary solution and its derivative) in the case of stability, as well as in a general case. Illustrative examples are shown and comparisons with known results are given.
1. Introduction
This paper will provide estimates of solutions of linear systems of neutral differential equations with constant coefficients and a constant delay:

where  is an independent variable,
is an independent variable,  is a constant delay,
is a constant delay,  , and
, and  are
are  constant matrices, and
constant matrices, and  is a column vector-solution. The sign "
is a column vector-solution. The sign " " denotes the left-hand derivative. Let
" denotes the left-hand derivative. Let  be a continuously differentiable vector-function. The solution
be a continuously differentiable vector-function. The solution  of problem (1.1), (1.2) on
of problem (1.1), (1.2) on  where
where

is defined in the classical sense (we refer, e.g., to [1]) as a function continuous on  continuously differentiable on
continuously differentiable on  except for points
except for points  ,
,  , and satisfying (1.1) everywhere on
, and satisfying (1.1) everywhere on  except for points
except for points  ,
,  .
.
The paper finds an estimate of the norm of the difference between a solution  of problem (1.1), (1.2) and the steady state
of problem (1.1), (1.2) and the steady state  at an arbitrary moment
at an arbitrary moment  .
.
Let  be a rectangular matrix. We will use the matrix norm:
be a rectangular matrix. We will use the matrix norm:

where the symbol  denotes the maximal eigenvalue of the corresponding square symmetric positive semidefinite matrix
denotes the maximal eigenvalue of the corresponding square symmetric positive semidefinite matrix  . Similarly,
. Similarly,  denotes the minimal eigenvalue of
denotes the minimal eigenvalue of  . We will use the following vector norms:
. We will use the following vector norms:

where  is a parameter.
is a parameter.
The most frequently used method for investigating the stability of functional-differential systems is the method of Lyapunov-Krasovskii functionals [2, 3]. Usually, it uses positive definite functionals of a quadratic form generated from terms of (1.1) and the integral (over the interval of delay [4]) of a quadratic form. A possible form of such a functional is then

where  and
and  are suitable
are suitable  positive definite matrices.
positive definite matrices.
Regarding the functionals of the form (1.5), we should underline the following. Using a functional (1.5), we can only obtain propositions concerning the stability. Statements such as that the expression

is bounded from above are of an integral type. Because the terms  in (1.5) contain differences, they do not imply the boundedness of the norm of
in (1.5) contain differences, they do not imply the boundedness of the norm of  itself.
itself.
Literature on the stability and estimation of solutions of neutral differential equations is enormous. Tracing previous investigations on this topic, we emphasize that a Lyapunov function  has been used to investigate the stability of systems (1.1) in [5] (see [6] as well). The stability of linear neutral systems of type (1.1), but with different delays
has been used to investigate the stability of systems (1.1) in [5] (see [6] as well). The stability of linear neutral systems of type (1.1), but with different delays  and
and  , is studied in [1] where a functional
, is studied in [1] where a functional

is used with suitable constants  and
and  . In [7, 8], functionals depending on derivatives are also suggested for investigating the asymptotic stability of neutral nonlinear systems. The investigation of nonlinear neutral delayed systems with two time dependent bounded delays in [9] to determine the global asymptotic and exponential stability uses, for example, functionals
. In [7, 8], functionals depending on derivatives are also suggested for investigating the asymptotic stability of neutral nonlinear systems. The investigation of nonlinear neutral delayed systems with two time dependent bounded delays in [9] to determine the global asymptotic and exponential stability uses, for example, functionals

where  and
and  are positive matrices and
are positive matrices and  is a positive scalar.
is a positive scalar.
Delay independent criteria of stability for some classes of delay neutral systems are developed in [10]. The stability of systems (1.1) with time dependent delays is investigated in [11]. For recent results on the stability of neutral equations, see [9, 12] and the references therein. The works in [12, 13] deal with delay independent criteria of the asymptotical stability of systems (1.1).
In this paper, we will use Lyapunov-Krasovskii quadratic type functionals of the dependent coordinates and their derivatives

and  , that is,
, that is,

where  is a solution of (1.1),
is a solution of (1.1),  and
and  are real parameters, the
are real parameters, the  matrices
matrices  ,
,  , and
, and  are positive definite, and
are positive definite, and  . The form of functionals (1.9) and (1.10) is suggested by the functionals (1.7)-(1.8). Although many approaches in the literature are used to judge the stability, our approach, among others, in addition to determining whether the system (1.1) is exponentially stable, also gives delay-dependent estimates of solutions in terms of the norms
. The form of functionals (1.9) and (1.10) is suggested by the functionals (1.7)-(1.8). Although many approaches in the literature are used to judge the stability, our approach, among others, in addition to determining whether the system (1.1) is exponentially stable, also gives delay-dependent estimates of solutions in terms of the norms  and
and  even in the case of instability. An estimate of the norm
even in the case of instability. An estimate of the norm  can be achieved by reducing the initial neutral system (1.1) to a neutral system having the same solution on the intervals indicated in which the "neutrality" is concentrated only on the initial interval. If, in the literature, estimates of solutions are given, then, as a rule, estimates of derivatives are not investigated.
can be achieved by reducing the initial neutral system (1.1) to a neutral system having the same solution on the intervals indicated in which the "neutrality" is concentrated only on the initial interval. If, in the literature, estimates of solutions are given, then, as a rule, estimates of derivatives are not investigated.
To the best of our knowledge, the general functionals (1.9) and (1.10) have not yet been applied as suggested to the study of stability and estimates of solutions of (1.1).
2. Exponential Stability and Estimates of the Convergence of Solutions to Stable Systems
First we give two definitions of stability to be used later on.
Definition 2.1.
The zero solution of the system of equations of neutral type (1.1) is called exponentially stable in the metric  if there exist constants
if there exist constants  ,
,  and
and  such that, for an arbitrary solution
such that, for an arbitrary solution  of (1.1), the inequality
of (1.1), the inequality

holds for  .
.
Definition 2.2.
The zero solution of the system of equations of neutral type (1.1) is called exponentially stable in the metric  if it is stable in the metric
if it is stable in the metric  and, moreover, there exist constants
and, moreover, there exist constants  ,
,  , and
, and  such that, for an arbitrary solution
such that, for an arbitrary solution  of (1.1), the inequality
of (1.1), the inequality

holds for  .
.
We will give estimates of solutions of the linear system (1.1) on the interval  using the functional (1.9). Then it is easy to see that an inequality
using the functional (1.9). Then it is easy to see that an inequality

holds on  . We will use an auxiliary
. We will use an auxiliary  -dimensional matrix:
-dimensional matrix:

depending on the parameter  and the matrices
and the matrices  ,
,  ,
,  . Next we will use the numbers
. Next we will use the numbers

The following lemma gives a representation of the linear neutral system (1.1) on an interval  in terms of a delayed system derived by an iterative process. We will adopt the customary notation
in terms of a delayed system derived by an iterative process. We will adopt the customary notation  where
where  is an integer,
is an integer,  is a positive integer, and
is a positive integer, and  denotes the function considered independently of whether it is defined for the arguments indicated or not.
denotes the function considered independently of whether it is defined for the arguments indicated or not.
Lemma 2.3.
Let  be a positive integer and
be a positive integer and  . Then a solution
. Then a solution  of the initial problem (1.1), (1.2) is a solution of the delayed system
of the initial problem (1.1), (1.2) is a solution of the delayed system

for  where
where  and
and  .
.
Proof.
For  the statement is obvious. If
the statement is obvious. If  , replacing
, replacing  by
by  , system (1.1) will turn into
, system (1.1) will turn into

Substituting (2.7) into (1.1), we obtain the following system of equations:

where  . If
. If  , replacing
, replacing  by
by  in (2.7), we get
in (2.7), we get

We do one more iteration substituting (2.9) into (2.8), obtaining

for  . Repeating this procedure
. Repeating this procedure  -times, we get the equation
-times, we get the equation

for  coinciding with (2.6).
coinciding with (2.6).
Remark 2.4.
The advantage of representing a solution of the initial problem (1.1), (1.2) as a solution of (2.6) is that, although (2.6) remains to be a neutral system, its right-hand side does not explicitly depend on the derivative  for
for  depending only on the derivative of the initial function on the initial interval
depending only on the derivative of the initial function on the initial interval  .
.
Now we give a statement on the stability of the zero solution of system (1.1) and estimates of the convergence of the solution, which we will prove using Lyapunov-Krasovskii functional (1.9).
Theorem 2.5.
Let there exist a parameter  and positive definite matrices
and positive definite matrices  ,
,  ,
,  such that matrix
such that matrix  is also positive definite. Then the zero solution of system (1.1) is exponentially stable in the metric
is also positive definite. Then the zero solution of system (1.1) is exponentially stable in the metric  . Moreover, for the solution
. Moreover, for the solution  of (1.1), (1.2) the inequality
of (1.1), (1.2) the inequality

holds on  where
where  .
.
Proof.
Let  . We will calculate the full derivative of the functional (1.9) along the solutions of system (1.1). We obtain
. We will calculate the full derivative of the functional (1.9) along the solutions of system (1.1). We obtain

For  , we substitute its value from (1.1) to obtain
, we substitute its value from (1.1) to obtain

Now it is easy to verify that the last expression can be rewritten as

or

Since the matrix  was assumed to be positive definite, for the full derivative of Lyapunov-Krasovskii functional (1.9), we obtain the following inequality:
was assumed to be positive definite, for the full derivative of Lyapunov-Krasovskii functional (1.9), we obtain the following inequality:

We will study the two possible cases (depending on the positive value of  ): either
): either

is valid or

holds.
-
(1)
Let (2.18) be valid. From (2.3) follows that
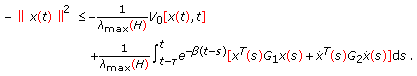 (2.20)
(2.20)
We use this expression in (2.17). Since  , we obtain (omitting terms
, we obtain (omitting terms  and
and  )
)

or

Due to (2.18) we have

Integrating this inequality over the interval  , we get
, we get

-
(2)
Let (2.19) be valid. From (2.3) we get
 (2.25)
(2.25)
We substitute this expression into inequality (2.17). Since  , we obtain (omitting terms
, we obtain (omitting terms  and
and  )
)

or

Since (2.19) holds, we have

Integrating this inequality over the interval  , we get
, we get

Combining inequalities (2.24), (2.29), we conclude that, in both cases (2.18), (2.19), we have

and, obviously (see (1.9)),

We use inequality (2.30) to obtain an estimate of the convergence of solutions of system (1.1). From (2.3) follows that

or (because  for nonnegative
for nonnegative  and
and  )
)

The last inequality implies

Thus inequality (2.12) is proved and, consequently, the zero solution of system (1.1) is exponentially stable in the metric  .
.
Theorem 2.6.
Let the matrix  be nonsingular and
be nonsingular and  . Let the assumptions of Theorem 2.5 with
. Let the assumptions of Theorem 2.5 with  and
and  be true. Then the zero solution of system (1.1) is exponentially stable in the metric
be true. Then the zero solution of system (1.1) is exponentially stable in the metric  . Moreover, for a solution
. Moreover, for a solution  of (1.1), (1.2), the inequality
of (1.1), (1.2), the inequality

where

holds on  .
.
Proof.
Let  . Then the exponential stability of the zero solution in the metric
. Then the exponential stability of the zero solution in the metric  is proved in Theorem 2.5. Now we will show that the zero solution is exponentially stable in the metric
is proved in Theorem 2.5. Now we will show that the zero solution is exponentially stable in the metric  as well. As follows from Lemma 2.3, for derivative
as well. As follows from Lemma 2.3, for derivative  , the inequality
, the inequality

holds if  We estimate
We estimate  and
and  using (2.12) and inequality
using (2.12) and inequality  . We obtain
. We obtain

Since

inequality (2.38) yields

Because  , we can estimate
, we can estimate

Then

Now we get from (2.40)

Since

the last inequality implies

The positive number  can be chosen arbitrarily large. Therefore, the last inequality holds for every
can be chosen arbitrarily large. Therefore, the last inequality holds for every  . We have obtained inequality (2.35) so that the zero solution of (1.1) is exponentially stable in the metric
. We have obtained inequality (2.35) so that the zero solution of (1.1) is exponentially stable in the metric  .
.
3. Estimates of Solutions in a General Case
Now we will estimate the norms of solutions of (1.1) and the norms of their derivatives in the case of the assumptions of Theorem 2.5 or Theorem 2.6 being not necessarily satisfied. It means that the estimates derived will cover the case of instability as well. For obtaining such type of results we will use a functional of Lyapunov-Krasovskii in the form (1.10). This functional includes an exponential factor, which makes it possible, in the case of instability, to get an estimate of the "divergence" of solutions. Functional (1.10) is a generalization of (1.9) because the choice  gives
gives  . For (1.10) the estimate
. For (1.10) the estimate

holds. We define an auxiliary  matrix
matrix

depending on the parameters  ,
,  and the matrices
and the matrices  ,
,  , and
, and  . The parameter
. The parameter  plays a significant role for the positive definiteness of the matrix
plays a significant role for the positive definiteness of the matrix  . Particularly, a proper choice of
. Particularly, a proper choice of  can cause the positivity of
can cause the positivity of  . In the following,
. In the following,  ,
,  and
and  , have the same meaning as in Part 2. The proof of the following theorem is similar to the proofs of Theorems 2.5 and 2.6 (and its statement in the case of
, have the same meaning as in Part 2. The proof of the following theorem is similar to the proofs of Theorems 2.5 and 2.6 (and its statement in the case of  exactly coincides with the statements of these theorems). Therefore, we will restrict its proof to the main points only.
exactly coincides with the statements of these theorems). Therefore, we will restrict its proof to the main points only.
Theorem 3.1.
-
(A)
Let
 be a fixed real number,
be a fixed real number, 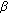 a positive constant, and
a positive constant, and 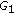 ,
, 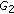 , and
, and  positive definite matrices such that the matrix
positive definite matrices such that the matrix  is also positive definite. Then a solution
is also positive definite. Then a solution 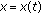 of problem (1.1), (1.2) satisfies on
of problem (1.1), (1.2) satisfies on 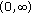 the inequality
the inequality 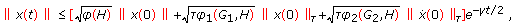 (3.3)
(3.3)
where  .
.
-
(B)
Let the matrix
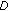 be nonsingular and
be nonsingular and  . Let all the assumptions of part (A) with
. Let all the assumptions of part (A) with 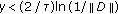 and
and 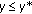 be true. Then the derivative of the solution
be true. Then the derivative of the solution 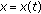 of problem (1.1), (1.2) satisfies on
of problem (1.1), (1.2) satisfies on  the inequality
the inequality 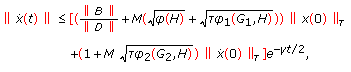 (3.4)
(3.4)
where  is defined by (2.36).
is defined by (2.36).
Proof.
Let  . We compute the full derivative of the functional (1.10) along the solutions of (1.1). For
. We compute the full derivative of the functional (1.10) along the solutions of (1.1). For  , we substitute its value from (1.1). Finally we get
, we substitute its value from (1.1). Finally we get

Since the matrix  is positive definite, we have
is positive definite, we have

Now we will study the two possible cases: either

is valid or

holds.
-
(1)
Let (3.7) be valid. Since
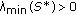 , from inequality (3.1) follows that
, from inequality (3.1) follows that  (3.9)
(3.9)
We use this inequality in (3.6). We obtain

From inequality (3.7) we get

Integrating this inequality over the interval  , we get
, we get

-
(2)
Let (3.8) be valid. From inequality (3.1) we get
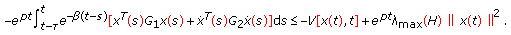 (3.13)
(3.13)
We use this inequality in (3.6) again. Since  , we get
, we get

Because the inequality (3.8) holds, we have

Integrating this inequality over the interval  , we get
, we get

Combining inequalities (3.12), (3.16), we conclude that, in both cases (3.7), (3.8), we have

From this, it follows

From the last inequality we derive inequality (3.3) in a way similar to that of the proof of Theorem 2.5. The inequality to estimate the derivative (3.4) can be obtained in much the same way as in the proof of Theorem 2.6.
Remark 3.2.
As can easily be seen from Theorem 3.1, part (A), if

we deal with an exponential stability in the metric  . If, moreover, part (B) holds and (3.19) is valid, then we deal with an exponential stability in the metric
. If, moreover, part (B) holds and (3.19) is valid, then we deal with an exponential stability in the metric  .
.
4. Examples
In this part we consider two examples. Auxiliary numerical computations were performed by using MATLAB & SIMULINK R2009a.
Example 4.1.
We will investigate system (1.1) where  ,
,  ,
,

that is, the system

with initial conditions (1.2). Set  and
and

For the eigenvalues of matrices  ,
,  , and
, and  , we get
, we get  ,
,  ,
,  ,
,  , and
, and  . The matrix
. The matrix  takes the form
takes the form

and  . Because all the eigenvalues are positive, matrix
. Because all the eigenvalues are positive, matrix  is positive definite. Since all conditions of Theorem 2.5 are satisfied, the zero solution of system (4.2) is asymptotically stable in the metric
is positive definite. Since all conditions of Theorem 2.5 are satisfied, the zero solution of system (4.2) is asymptotically stable in the metric  . Further we have
. Further we have

Since  , all conditions of Theorem 2.6 are satisfied and, consequently, the zero solution of (4.2), (35) is asymptotically stable in the metric
, all conditions of Theorem 2.6 are satisfied and, consequently, the zero solution of (4.2), (35) is asymptotically stable in the metric  . Finally, from (2.12) and (2.35) follows that the inequalities
. Finally, from (2.12) and (2.35) follows that the inequalities

hold on  .
.
Example 4.2.
We will investigate system (1.1) where  ,
,  ,
,

that is, the system

with initial conditions (1.2). Set  and
and

For the eigenvalues of matrices  ,
,  , and
, and  , we get
, we get  ,
,  ,
, 
 , and
, and  . The matrix
. The matrix  takes the form
takes the form

and  . Because all eigenvalues are positive, matrix
. Because all eigenvalues are positive, matrix  is positive definite. Since all conditions of Theorem 2.5 are satisfied, the zero solution of system (4.8) is asymptotically stable in the metric
is positive definite. Since all conditions of Theorem 2.5 are satisfied, the zero solution of system (4.8) is asymptotically stable in the metric  . Further we have
. Further we have

Since  , all conditions of Theorem 2.6 are satisfied and, consequently, the zero solution of (4.8) is asymptotically stable in the metric
, all conditions of Theorem 2.6 are satisfied and, consequently, the zero solution of (4.8) is asymptotically stable in the metric  . Finally, from (2.12) and (2.35) follows that the inequalities
. Finally, from (2.12) and (2.35) follows that the inequalities

hold on  .
.
Remark 4.3.
In [12] an example can be found similar to Example 4.2 with the same matrices  ,
,  , arbitrary constant positive
, arbitrary constant positive  , and with a matrix
, and with a matrix

where  is a real parameter. The stability is established for
is a real parameter. The stability is established for  . In recent paper [13], the stability of the same system is even established for
. In recent paper [13], the stability of the same system is even established for  .
.
Comparing these particular results with Example 4.2, we see that, in addition to stability, our results imply the exponential stability in the metric  as well as in the metric
as well as in the metric  . Moreover, we are able to prove the exponential stability (in
. Moreover, we are able to prove the exponential stability (in  as well as in
as well as in  ) in Example 4.2 with the matrix
) in Example 4.2 with the matrix  for
for  and for an arbitrary constant delay
and for an arbitrary constant delay  . The latter statement can be explained easily—for an arbitrary positive
. The latter statement can be explained easily—for an arbitrary positive  , we set
, we set  . Calculating the characteristic equation for the matrix
. Calculating the characteristic equation for the matrix  where
where  is changed by
is changed by  we get
we get

where

It is easy to verify that  for
for  and
and  , and for the equation
, and for the equation

we have  . Then, due to the symmetry of the real matrix
. Then, due to the symmetry of the real matrix  , we conclude that, by Descartes' rule of signs, all eigenvalues of
, we conclude that, by Descartes' rule of signs, all eigenvalues of  (i.e., all roots of
(i.e., all roots of  ) are positive. This means that the exponential stability (in the metric
) are positive. This means that the exponential stability (in the metric  as well as in the metric
as well as in the metric  ) for
) for  is proved. Finally, we note that the variation of
is proved. Finally, we note that the variation of  within the interval indicated or the choice
within the interval indicated or the choice  does not change the exponential stability having only influence on the form of the final inequalities for
does not change the exponential stability having only influence on the form of the final inequalities for  and
and  .
.
5. Conclusions
In this paper we derived statements on the exponential stability of system (1.1) as well as on estimates of the norms of its solutions and their derivatives in the case of exponential stability and in the case of exponential stability being not guaranteed. To obtain these results, special Lyapunov functionals in the form (1.9) and (1.10) were utilized as well as a method of constructing a reduced neutral system with the same solution on the intervals indicated as the initial neutral system (1.1). The flexibility and power of this method was demonstrated using examples and comparisons with other results in this field. Considering further possibilities along these lines, we conclude that, to generalize the results presented to systems with bounded variable delay  , a generalization is needed of Lemma 2.3 to the above reduced neutral system. This can cause substantial difficulties in obtaining results which are easily presentable. An alternative would be to generalize only the part of the results related to the exponential stability in the metric
, a generalization is needed of Lemma 2.3 to the above reduced neutral system. This can cause substantial difficulties in obtaining results which are easily presentable. An alternative would be to generalize only the part of the results related to the exponential stability in the metric  and the related estimates of the norms of solutions in the case of exponential stability and in the case of the exponential stability being not guaranteed (omitting the case of exponential stability in the metric
and the related estimates of the norms of solutions in the case of exponential stability and in the case of the exponential stability being not guaranteed (omitting the case of exponential stability in the metric  and estimates of the norm of a derivative of solution). Such an approach will probably permit a generalization to variable matrices (
and estimates of the norm of a derivative of solution). Such an approach will probably permit a generalization to variable matrices ( ,
,  ,
,  ) and to a variable delay (
) and to a variable delay ( ) or to two different variable delays. Nevertheless, it seems that the results obtained will be very cumbersome and hardly applicable in practice.
) or to two different variable delays. Nevertheless, it seems that the results obtained will be very cumbersome and hardly applicable in practice.
References
Kolmanovskii V, Myshkis A: Introduction to the Theory and Applications of Functional-Differential Equations, Mathematics and its Applications. Volume 463. Kluwer Academic Publishers, Dordrecht, the Netherlands; 1999:xvi+648.
Krasovskii NN: Some Problems of Theory of Stability of Motion. Fizmatgiz, Moscow, Russia; 1959.
Krasovskiĭ NN: Stability of Motion. Applications of Lyapunov's Second Method to Differential systems and Equations with Delay, Translated by J. L. Brenner. Stanford University Press, Stanford, Calif, USA; 1963:vi+188.
Korenevskiĭ DG: Stability of Dynamical Systems Under Random Perturbations of Parameters. Algebraic Criteria. Naukova Dumka, Kiev, Ukraine; 1989:208.
Khusainov DYa, Yunkova EA: Investigation of the stability of linear systems of neutral type by the method of Lyapunov functions. Differentsial cprime nye Uravneniya 1988,24(4):613-621. Translated in Differential Equations, vol. 24, no. 4, pp. 424–431
Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Pynamics, Mathematics and its Applications. Volume 74. Kluwer Academic Publishers, Dordrecht, the Netherlands; 1992:xii+501.
Kolmanovskiĭ V, Myshkis A: Applied Theory of Functional-Differential Equations, Mathematics and its Applications (Soviet Series). Volume 85. Kluwer Academic Publishers Group, Dordrecht, the Netherlands; 1992:xvi+234.
Kolmanovskiĭ V, Nosov V: Stability of Functional Differential Equations, Mathematics in Science and Engineering. Volume 180. Academic Press, Harcourt Brace Jovanovich, London, UK; 1986:xiv+ 217.
Mei-Gin L: Stability analysis of neutral-type nonlinear delayed systems: an LMI approach. Journal of Zhejiang University A 2006, 7, supplement 2: 237-244.
Gu K, Kharitonov VL, Chen J: Stability of Time-Delay Systems, Control Engineering. Birkhuser, Boston, Mass, USA; 2003:xx+353.
Liao X, Wang L, Yu P: Stability of Dynamical Systems, Monograph Series on Nonlinear Science and Complexity. Volume 5. Elsevier, Amsterdam, the Netherlands; 2007:xii+706.
Park Ju-H, Won S: A note on stability of neutral delay-differential systems. Journal of the Franklin Institute 1999,336(3):543-548. 10.1016/S0016-0032(98)00040-4
Liu X-x, Xu B: A further note on stability criterion of linear neutral delay-differential systems. Journal of the Franklin Institute 2006,343(6):630-634. 10.1016/j.jfranklin.2006.02.024
Acknowledgments
J. Baštinec was supported by Grant 201/10/1032 of Czech Grant Agency, by the Council of Czech Government MSM 0021630529, and by Grant FEKT-S-10-3 of Faculty of Electrical Engineering and Communication, Brno University of Technology. J. Diblík was supported by Grant 201/08/9469 of Czech Grant Agency, by the Council of Czech Government MSM 0021630503, MSM 0021630519, and by Grant FEKT-S-10-3 of Faculty of Electrical Engineering and Communication, Brno University of Technology. D. Ya. Khusainov was supported by project M/34-2008 MOH Ukraine since March 27, 2008. A. Ryvolová was supported by the Council of Czech Government MSM 0021630529, and by Grant FEKT-S-10-3 of Faculty of Electrical Engineering and Communication.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Baštinec, J., Diblík, J., Khusainov, D.Y. et al. Exponential Stability and Estimation of Solutions of Linear Differential Systems of Neutral Type with Constant Coefficients. Bound Value Probl 2010, 956121 (2010). https://doi.org/10.1155/2010/956121
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/956121
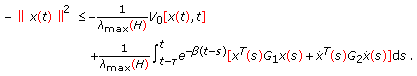

 be a fixed real number,
be a fixed real number, 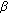 a positive constant, and
a positive constant, and 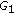 ,
, 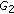 , and
, and  positive definite matrices such that the matrix
positive definite matrices such that the matrix  is also positive definite. Then a solution
is also positive definite. Then a solution 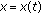 of problem (1.1), (1.2) satisfies on
of problem (1.1), (1.2) satisfies on 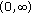 the inequality
the inequality 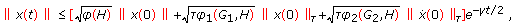
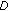 be nonsingular and
be nonsingular and  . Let all the assumptions of part (A) with
. Let all the assumptions of part (A) with 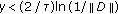 and
and 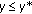 be true. Then the derivative of the solution
be true. Then the derivative of the solution 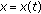 of problem (1.1), (1.2) satisfies on
of problem (1.1), (1.2) satisfies on  the inequality
the inequality 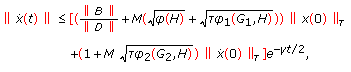
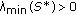 , from inequality (3.1) follows that
, from inequality (3.1) follows that