- Research Article
- Open access
- Published:
Existence of Positive Solutions for Nonlinear Eigenvalue Problems
Boundary Value Problems volume 2010, Article number: 961496 (2010)
Abstract
We use a fixed point theorem in a cone to obtain the existence of positive solutions of the differential equation,  ,
,  , with some suitable boundary conditions, where
, with some suitable boundary conditions, where  is a parameter.
is a parameter.
1. Introduction
We consider the existence of positive solutions of the following two-point boundary value problem:

where  and
and  are nonnegative constants, and
are nonnegative constants, and  .
.
In the last thirty years, there are many mathematician considered the boundary value problem (BVP
λ
) with  , see, for example, Chu et al. [1], Chu et al. [2], Chu and Zhau [3], Chu and Jiang [4], Coffman and Marcus [5], Cohen and Keller [6], Erbe [7], Erbe et al. [8], Erbe and Wang [9], Guo and Lakshmikantham [10], Iffland [11], Njoku and Zanolin [12], Santanilla [13].
, see, for example, Chu et al. [1], Chu et al. [2], Chu and Zhau [3], Chu and Jiang [4], Coffman and Marcus [5], Cohen and Keller [6], Erbe [7], Erbe et al. [8], Erbe and Wang [9], Guo and Lakshmikantham [10], Iffland [11], Njoku and Zanolin [12], Santanilla [13].
In 1993, Wong [14] showed the following excellent result.
Theorem 1 A (see [14]).
Assume that

is an increasing function with respect to  . If there exists a constant
. If there exists a constant  such that
such that

where  for
for  , then, there exists
, then, there exists  such that the boundary value problem (BVP
λ
) with
such that the boundary value problem (BVP
λ
) with  has a positive solution in
has a positive solution in  for
for  , while there is no such solution for
, while there is no such solution for  in which
in which 
Seeing such facts, we cannot but ask "whether or not we can obtain a similar conclusion for the boundary value problem (BVP λ )." We give a confirm answer to the question.
First, We observe the following statements.
(1)Let

on  , then
, then  is the Green's function of the differential equation
is the Green's function of the differential equation  in
in  with respect to the boundary value condition
with respect to the boundary value condition  .
.
(2) , is a cone in the Banach space with
, is a cone in the Banach space with  .
.
In order to discuss our main result, we need the follo wing useful lemmas which due to Lian et al. [15] and Guo and Lakshmikantham [10], respectively.
Lemma 1 B (see [10]).
Suppose that  be defined as in
be defined as in  . Then, we have the following results.
. Then, we have the following results.
 for
for  and
and  )
)
 for
for  and
and  )
)
Lemma 1 C (see [10, Lemmas  and
and  ]).
]).
Let  be a real Banach space, and let
be a real Banach space, and let  be a cone. Assume that
be a cone. Assume that  and
and  is completely continuous. Then
is completely continuous. Then
(1) if
if

(2)
where  is the fixed point index of a compact map
is the fixed point index of a compact map  , such that
, such that  for
for  , with respect to
, with respect to  .
.
2. Main Results
Now, we can state and prove our main result.
Theorem 2.1.
Suppose that there exist two distinct positive constants  ,
,  and a function
and a function  with
with  and
and  such that
such that


Then (BVP
λ
) has a positive solution  with
with  between
between  and
and  if
if

where

Proof.
It is clear that (BVP
λ
) has a solution  if, and only if,
if, and only if,  is the solution of the operator equation
is the solution of the operator equation

It follows from the definition of  in our observation
in our observation  and Lemma B that
and Lemma B that

Hence,  , which implies
, which implies  . Furthermore, it is easy to check that
. Furthermore, it is easy to check that  is completely continuous. If there exists a
is completely continuous. If there exists a  such that
such that  , then we obtain the desired result. Thus, we may assume that
, then we obtain the desired result. Thus, we may assume that

where  and
and  . We now separate the rest proof into the following three steps.
. We now separate the rest proof into the following three steps.
Step 1.
It follows from the definitions of  and
and  that, for
that, for  ,
,

which implies

Hence, by (2.5),

which implies

Hence

We now claim that

In fact, if there exist  and
and  such that
such that  then, by (2.11),
then, by (2.11),

which gives a contradiction. This proves that (2.13) holds. Thus, by Lemma C,

Step 2.
First, we claim that

Suppose to the contrary that there exist  and
and  such that
such that

It is clear that (2.17) is equivalent to

Since  and
and  it follows that there exists a
it follows that there exists a  such that
such that

Let

Then  . From
. From  on
on  , we see that
, we see that  on
on  on
on  and
and  on
on  . It follows from
. It follows from

and  on
on  that
that

Hence,

Thus

This contradiction implies

Therefore, by Lemma C,

Step 3.
It follows from Steps (1) and (2) and the property of the fixed point index (see, for example, [10, Theorem  ]) that the proof is complete.
]) that the proof is complete.
Remark 2.2.
It follows from the conclusion of Theorem 2.1 that the positive constant  and nonnegative function
and nonnegative function  satisfy
satisfy

There are many functions  and positive constants
and positive constants  satisfying (2.27). For example, Suppose that
satisfying (2.27). For example, Suppose that  and
and  . Let
. Let  on
on  , then
, then  on
on  and
and

Remark 2.3.
We now define

A simple calculation shows that

Then, we have the following results.
(i)Suppose that  . Taking
. Taking  , there exists
, there exists  (
( can be chosen small arbitrarily) such that
can be chosen small arbitrarily) such that

Hence,

It follows from Remark 2.2 that the hypothesis (2.2) of Theorem 2.1 is satisfied if  .
.
(ii)Suppose that  . Taking
. Taking  , there exists
, there exists  (
( can be chosen large arbitrarily) such that
can be chosen large arbitrarily) such that

Hence,

which satisfies the hypothesis (2.1) of Theorem 2.1.
(iii)Suppose that  . Taking
. Taking  , there exists
, there exists  (
( can be chosen small arbitrarily) such that
can be chosen small arbitrarily) such that

Hence,

which satisfies the hypothesis (2.1) of Theorem 2.1.
(iv)Suppose that  . Taking
. Taking  , there exists a
, there exists a  (
( can be chosen large arbitrarily) such that
can be chosen large arbitrarily) such that

Hence, we have the following two cases.
Case i.
Assume that  is bounded, say
is bounded, say

for some constant  . Taking
. Taking  (since
(since  can be chosen large arbitrarily,
can be chosen large arbitrarily,  can be chosen large arbitrarily, too),
can be chosen large arbitrarily, too),

Case ii.
Assume that  is unbounded, then there exist a
is unbounded, then there exist a  (
( can be chosen large arbitrarily) and
can be chosen large arbitrarily) and  such that
such that

It follows from  and (2.37) that
and (2.37) that

By Cases (i), (ii) and Remark 2.2, we see that the hypothesis (2.2) of Theorem 2.1 is satisfied if  .
.
We immediately conclude the following corollaries.
Corollary 2.4.
(BVP
λ
) has at least one positive solution for  if one of the following conditions holds:
if one of the following conditions holds:


Proof.
It follows from Remark 2.3 and Theorem 2.1 that the desired result holds, immediately.
Corollary 2.5.
Let

 on
on  for some
for some  and
and  .
.
Then, for  , (BVP
λ
) has at least two positive solutions
, (BVP
λ
) has at least two positive solutions  and
and  such that
such that

Proof.
It follows from Remark 2.3 that there exist two real numbers  satisfying
satisfying

Hence, by Theorem 2.1 and Remark 2.2, we see that for each  , there exist two positive solutions
, there exist two positive solutions  and
and  of (BVP
λ
) such that
of (BVP
λ
) such that

Thus, we complete the proof.
Corollary 2.6.
Let

 on
on  , for some
, for some  .
.
Then, for  , (BVP
λ
) has at least two positive solutions
, (BVP
λ
) has at least two positive solutions  and
and  such that
such that

Proof.
It follows from Remark 2.3 that there exist two real numbers  satisfying
satisfying

Hence, by Theorem 2.1 and Remark 2.2, we see that, for each  , (BVP
λ
) has two positive solutions
, (BVP
λ
) has two positive solutions  and
and  such that
such that

Thus, we completed the proof.
3. Examples
To illustrate the usage of our results, we present the following examples.
Example 3.1.
Consider the following boundary value problem:

Clearly,

If we take  , then it follows from
, then it follows from  of Corollary 2.4 that (BVP.1) has a solution if
of Corollary 2.4 that (BVP.1) has a solution if  .
.
Example 3.2.
Consider the following boundary value problem:

Clearly,

If we take  , then it follows from
, then it follows from  of Corollary 2.4 that (BVP.2) has a solution if
of Corollary 2.4 that (BVP.2) has a solution if  .
.
Example 3.3.
Consider the following boundary value problem:

Clearly, if we take  and
and  ,
,

Hence, it follows from Corollary 2.5 that (BVP.3) has two solutions if  .
.
References
Chu J, Chen H, O'Regan D: Positive periodic solutions and eigenvalue intervals for systems of second order differential equations. Mathematische Nachrichten 2008,281(11):1549-1556. 10.1002/mana.200510695
Chu J, O'Regan D, Zhang M: Positive solutions and eigenvalue intervals for nonlinear systems. Proceedings of the Indian Academy of Sciences 2007,117(1):85-95. 10.1007/s12044-007-0007-z
Chu J, Zhou Z: Positive solutions and eigenvalues of nonlocal boundary-value problems. Electronic Journal of Differential Equations 2005, (86):1-9.
Chu J, Jiang D:Eigenvalues and discrete boundary value problems for the one-dimensional
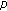 -Laplacian. Journal of Mathematical Analysis and Applications 2005,305(2):452-465. 10.1016/j.jmaa.2004.10.055
-Laplacian. Journal of Mathematical Analysis and Applications 2005,305(2):452-465. 10.1016/j.jmaa.2004.10.055Coffman CV, Marcus M: Existence and uniqueness results for semi-linear Dirichlet problems in annuli. Archive for Rational Mechanics and Analysis 1989,108(4):293-307.
Cohen DS, Keller HB: Some positone problems suggested by nonlinear heat generation. Journal of Mathematics and Mechanics 1967, 16: 1361-1376.
Erbe LH: Existence of solutions to boundary value problems for second order differential equations. Nonlinear Analysis: Theory, Methods & Applications 1982,6(11):1155-1162. 10.1016/0362-546X(82)90027-X
Erbe LH, Hu S, Wang H: Multiple positive solutions of some boundary value problems. Journal of Mathematical Analysis and Applications 1994,184(3):640-648. 10.1006/jmaa.1994.1227
Erbe LH, Wang H: On the existence of positive solutions of ordinary differential equations. Proceedings of the American Mathematical Society 1994,120(3):743-748. 10.1090/S0002-9939-1994-1204373-9
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Iffland G: Positive solution of a problem of Emden-Fowler type with a free boundary. SIAM Journal on Mathematical Analysis 1987,18(2):283-292. 10.1137/0518022
Njoku FI, Zanolin F: Positive solutions for two-point BVPs: existence and multiplicity results. Nonlinear Analysis: Theory, Methods & Applications 1989,13(11):1329-1338. 10.1016/0362-546X(89)90016-3
Santanilla J: Nonnegative solutions to boundary value problems for nonlinear first and second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1987,126(2):397-408. 10.1016/0022-247X(87)90049-7
Wong FH: Existence of positive solutions of singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 1993,21(5):397-406. 10.1016/0362-546X(93)90083-5
Lian W-C, Wong FH, Yeh CC: On the existence of positive solutions of nonlinear second order differential equations. Proceedings of the American Mathematical Society 1996,124(4):1117-1126. 10.1090/S0002-9939-96-03403-X
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, SP., Wong, FH. & Kung, FK. Existence of Positive Solutions for Nonlinear Eigenvalue Problems. Bound Value Probl 2010, 961496 (2010). https://doi.org/10.1155/2010/961496
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/961496
 -Laplacian. Journal of Mathematical Analysis and Applications 2005,305(2):452-465. 10.1016/j.jmaa.2004.10.055
-Laplacian. Journal of Mathematical Analysis and Applications 2005,305(2):452-465. 10.1016/j.jmaa.2004.10.055