- Research Article
- Open access
- Published:
Solutions and Green's Functions for Boundary Value Problems of Second-Order Four-Point Functional Difference Equations
Boundary Value Problems volume 2010, Article number: 973731 (2010)
Abstract
We consider the Green's functions and the existence of positive solutions for a second-order functional difference equation with four-point boundary conditions.
1. Introduction
In recent years, boundary value problems (BVPs) of differential and difference equations have been studied widely and there are many excellent results (see Gai et al. [1], Guo and Tian [2], Henderson and Peterson [3], and Yang et al. [4]). By using the critical point theory, Deng and Shi [5] studied the existence and multiplicity of the boundary value problems to a class of second-order functional difference equations

with boundary value conditions

where the operator  is the Jacobi operator
is the Jacobi operator

Ntouyas et al. [6] and Wong [7] investigated the existence of solutions of a BVP for functional differential equations

where  is a continuous function,
is a continuous function,  , and
, and  .
.
Weng and Guo [8] considered the following two-point BVP for a nonlinear functional difference equation with  -Laplacian operator
-Laplacian operator

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  is continuous,
is continuous,  .
.
Yang et al. [9] considered two-point BVP of the following functional difference equation with  -Laplacian operator:
-Laplacian operator:

where  ,
,  , and
, and  ,
,  ,
,  , and
, and  are nonnegative real constants.
are nonnegative real constants.
For  and
and  , let
, let

Then  and
and  are both Banach spaces endowed with the max-norm
are both Banach spaces endowed with the max-norm

For any real function  defined on the interval
defined on the interval  and any
and any  with
with  , we denote by
, we denote by  an element of
an element of  defined by
defined by  ,
,  .
.
In this paper, we consider the following second-order four-point BVP of a nonlinear functional difference equation:

where  and
and  ,
,  ,
,  ,
,  ,
,  is a continuous function,
is a continuous function,  and
and  for
for  ,
,  ,
,  , and
, and  are nonnegative real constants, and
are nonnegative real constants, and  for
for  .
.
At this point, it is necessary to make some remarks on the first boundary condition in (1.9). This condition is a generalization of the classical condition

from ordinary difference equations. Here this condition connects the history  with the single
with the single  . This is suggested by the well-posedness of BVP (1.9), since the function
. This is suggested by the well-posedness of BVP (1.9), since the function  depends on the term
depends on the term  (i.e., past values of
(i.e., past values of  ).
).
As usual, a sequence  is said to be a positive solution of BVP (1.9) if it satisfies BVP (1.9) and
is said to be a positive solution of BVP (1.9) if it satisfies BVP (1.9) and  for
for  with
with  for
for  .
.
2. The Green's Function of (1.9)
First we consider the nonexistence of positive solutions of (1.9). We have the following result.
Lemma 2.1.
Assume that

or

Then (1.9) has no positive solution.
Proof.
From  , we know that
, we know that  is convex for
is convex for  .
.
Assume that  is a positive solution of (1.9) and (2.1) holds.
is a positive solution of (1.9) and (2.1) holds.
-
(1)
Consider that
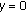 .
.
If  , then
, then  . It follows that
. It follows that

which is a contradiction to the convexity of  .
.
If  , then
, then  . If
. If  , then we have
, then we have

Hence

which is a contradiction to the convexity of  . If
. If  for
for  , then
, then  is a trivial solution. So there exists a
is a trivial solution. So there exists a  such that
such that  .
.
We assume that  . Then
. Then

Hence

which is a contradiction to the convexity of  .
.
If  , similar to the above proof, we can also get a contradiction.
, similar to the above proof, we can also get a contradiction.
-
(2)
Consider that
 .
.
Now we have

which is a contradiction to the convexity of  .
.
Assume that  is a positive solution of (1.9) and (2.2) holds.
is a positive solution of (1.9) and (2.2) holds.
-
(1)
Consider that
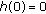 .
.
If  , then we obtain
, then we obtain

which is a contradiction to the convexity of  .
.
If  , similar to the above proof, we can also get a contradiction.
, similar to the above proof, we can also get a contradiction.
If  , and so
, and so  , then there exists a
, then there exists a  such that
such that  . Otherwise,
. Otherwise,  is a trivial solution. Assume that
is a trivial solution. Assume that  , then
, then

which implies that

A contradiction to the convexity of  follows.
follows.
If  , we can also get a contradiction.
, we can also get a contradiction.
-
(2)
Consider that
 .
.
Now we obtain

which is a contradiction to the convexity of  .
.
Next, we consider the existence of the Green's function of equation

We always assume that
( )
)  ,
,  and
and  .
.
Motivated by Zhao [10], we have the following conclusions.
Theorem 2.2.
The Green's function for second-order four-point linear BVP (2.13) is given by

where

Proof.
Consider the second-order two-point BVP

It is easy to find that the solution of BVP (2.16) is given by


The three-point BVP

can be obtained from replacing  by
by  in (2.16). Thus we suppose that the solution of (2.19) can be expressed by
in (2.16). Thus we suppose that the solution of (2.19) can be expressed by

where  and
and  are constants that will be determined.
are constants that will be determined.
From (2.18) and (2.20), we have

Putting the above equations into (2.19) yields

By (H ), we obtain
), we obtain  and
and  by solving the above equation:
by solving the above equation:

By (2.19) and (2.20), we have

The four-point BVP (2.13) can be obtained from replacing  by
by  in (2.19). Thus we suppose that the solution of (2.13) can be expressed by
in (2.19). Thus we suppose that the solution of (2.13) can be expressed by

where  and
and  are constants that will be determined.
are constants that will be determined.
From (2.24) and (2.25), we get

Putting the above equations into (2.13) yields

By (H ), we can easily obtain
), we can easily obtain

Then by (2.17), (2.20), (2.23), (2.25), and (2.28), the solution of BVP (2.13) can be expressed by

where  is defined in (2.14). That is,
is defined in (2.14). That is,  is the Green's function of BVP (2.13).
is the Green's function of BVP (2.13).
Remark 2.3.
By (H ), we can see that
), we can see that  for
for  . Let
. Let

Then  .
.
Lemma 2.4.
Assume that ( ) holds. Then the second-order four-point BVP (2.13) has a unique solution which is given in (2.29).
) holds. Then the second-order four-point BVP (2.13) has a unique solution which is given in (2.29).
Proof.
We need only to show the uniqueness.
Obviously,  in (2.29) is a solution of BVP (2.13). Assume that
in (2.29) is a solution of BVP (2.13). Assume that  is another solution of BVP (2.13). Let
is another solution of BVP (2.13). Let

Then by (2.13), we have


From (2.32) we have, for  ,
,

which implies that

Combining (2.33) with (2.35), we obtain

Condition (H ) implies that (2.36) has a unique solution
) implies that (2.36) has a unique solution  . Therefore
. Therefore  for
for  . This completes the proof of the uniqueness of the solution.
. This completes the proof of the uniqueness of the solution.
3. Existence of Positive Solutions
In this section, we discuss the BVP (1.9).
Assume that  ,
,  .
.
We rewrite BVP (1.9) as

with  .
.
Suppose that  is a solution of the BVP (3.1). Then it can be expressed as
is a solution of the BVP (3.1). Then it can be expressed as

Lemma 3.1 (see Guo et al. [11]).
Assume that  is a Banach space and
is a Banach space and  is a cone in
is a cone in  . Let
. Let  . Furthermore, assume that
. Furthermore, assume that  is a completely continuous operator and
is a completely continuous operator and  for
for  . Thus, one has the following conclusions:
. Thus, one has the following conclusions:
-
(1)
if
 for
for  , then
, then  ;
; -
(2)
if
 for
for  , then
, then 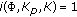 .
.
Assume that  . Then (3.1) may be rewritten as
. Then (3.1) may be rewritten as

Let  be a solution of (3.3). Then by (3.2) and
be a solution of (3.3). Then by (3.2) and  , it can be expressed as
, it can be expressed as

Let  be a solution of BVP (3.1) and
be a solution of BVP (3.1) and  . Then for
. Then for  we have
we have  and
and

Let

Then  is a Banach space endowed with norm
is a Banach space endowed with norm  and
and  is a cone in
is a cone in  .
.
For  , we have by (H
, we have by (H ) and the definition of
) and the definition of  ,
,

For every  ,
,  , by the definition of
, by the definition of  and (3.5), if
and (3.5), if  , we have
, we have

If  , we have, by (3.4),
, we have, by (3.4),

hence by the definition of  , we obtain for
, we obtain for 

Lemma 3.2.
For every  , there is
, there is  , such that
, such that

Proof.
For  , and
, and  , by the definitions of
, by the definitions of  and
and  , we have
, we have

Obviously, there is a  , such that (3.11) holds.
, such that (3.11) holds.
Define an operator  by
by

Then we may transform our existence problem of positive solutions of BVP (3.1) into a fixed point problem of operator (3.13).
Lemma 3.3.
Consider that  .
.
Proof.
If  and
and  ,
,  and
and  , respectively. Thus, (H
, respectively. Thus, (H ) yields
) yields

It follows from the definition of  that
that

which implies that  .
.
Lemma 3.4.
Suppose that ( ) holds. Then
) holds. Then  is completely continuous.
is completely continuous.
We assume that
(H )
)
(H )
) .
.
We have the following main results.
Theorem 3.5.
Assume that ( )–(
)–( ) hold. Then BVP (3.1) has at least one positive solution if the following conditions are satisfied:
) hold. Then BVP (3.1) has at least one positive solution if the following conditions are satisfied:
(H ) there exists a
) there exists a  such that, for
such that, for  , if
, if  , then
, then  ;
;
(H ) there exists a
) there exists a  such that, for
such that, for  , if
, if  , then
, then 
or
(H )
) ;
;
(H ) there exists a
) there exists a  such that, for
such that, for  , if
, if  , then
, then  ;
;
(H ) there exists an
) there exists an  , such that, for
, such that, for  , if
, if  , then
, then 
where

Proof.
Assume that ( ) and (
) and ( ) hold. For every
) hold. For every  , we have
, we have  , thus
, thus

which implies by Lemma 3.1 that

For every  , by (3.8)–(3.10) and Lemma 3.2, we have, for
, by (3.8)–(3.10) and Lemma 3.2, we have, for  ,
,  . Then by (3.13) and (
. Then by (3.13) and ( ), we have
), we have

which implies by Lemma 3.1 that

So by (3.18) and (3.20), there exists one positive fixed point  of operator
of operator  with
with  .
.
Assume that ( )–(
)–( ) hold, for every
) hold, for every  and
and  ,
,  , by (
, by ( ), we have
), we have

Thus we have from Lemma 3.1 that

For every  , by (3.8)–(3.10), we have
, by (3.8)–(3.10), we have  ,
,

Thus we have from Lemma 3.1 that

So by (3.22) and (3.24), there exists one positive fixed point  of operator
of operator  with
with  .
.
Consequently,  or
or  is a positive solution of BVP (3.1).
is a positive solution of BVP (3.1).
Theorem 3.6.
Assume that ( )–(
)–( ) hold. Then BVP (3.1) has at least one positive solution if (
) hold. Then BVP (3.1) has at least one positive solution if ( ) and (
) and ( ) or (
) or ( ) and (
) and ( ) hold.
) hold.
Theorem 3.7.
Assume that ( )–(
)–( ) hold. Then BVP (3.1) has at least two positive solutions if (H
) hold. Then BVP (3.1) has at least two positive solutions if (H ), (H
), (H ), and (H
), and (H ) or (H
) or (H ), (H
), (H ), and (H
), and (H ) hold.
) hold.
Theorem 3.8.
Assume that (H )–(H
)–(H ) hold. Then BVP (3.1) has at least three positive solutions if (H
) hold. Then BVP (3.1) has at least three positive solutions if (H )–(H
)–(H ) hold.
) hold.
Assume that  ,
,  , and
, and
( )
) 
Define  as follows:
as follows:

which satisfies
 H
H .
.
Obviously,  exists.
exists.
Assume that  is a solution of (1.9). Let
is a solution of (1.9). Let

where

By (1.9), (3.26), (3.27), (H ), (H
), (H ), and the definition of
), and the definition of  , we have
, we have


and, for  ,
,

Let

Then by (3.27), (H ), (H
), (H ), and the definition of
), and the definition of  , we have
, we have  for
for  Thus, the BVP (1.9) can be changed into the following BVP:
Thus, the BVP (1.9) can be changed into the following BVP:

with  and
and  .
.
Similar to the above proof, we can show that (1.9) has at least one positive solution. Consequently, (1.9) has at least one positive solution.
Example 3.9.
Consider the following BVP:

That is,

Then we obtain

Let

where 
By calculation, we can see that (H )–(H
)–(H ) hold, then by Theorem 3.8, the BVP (3.33) has at least three positive solutions.
) hold, then by Theorem 3.8, the BVP (3.33) has at least three positive solutions.
4. Eigenvalue Intervals
In this section, we consider the following BVP with parameter  :
:

with  .
.
The BVP (4.1) is equivalent to the equation

Let  be the solution of (3.3),
be the solution of (3.3),  . Then we have
. Then we have

Let  and
and  be defined as the above. Define
be defined as the above. Define  by
by

Then solving the BVP (4.1) is equivalent to finding fixed points in  . Obviously
. Obviously  is completely continuous and keeps the
is completely continuous and keeps the  invariant for
invariant for  .
.
Define

respectively. We have the following results.
Theorem 4.1.
Assume that (H ), (H
), (H ), (H
), (H ),
),
(H )
)  ,
,
(H )
) 
hold, where  , then BVP (4.1) has at least one positive solution, where
, then BVP (4.1) has at least one positive solution, where  is a positive constant.
is a positive constant.
Proof.
Assume that condition (H ) holds. If
) holds. If  and
and  , there exists an
, there exists an  sufficiently small, such that
sufficiently small, such that

By the definition of  , there is an
, there is an  , such that for
, such that for  ,
,

It follows that, for  and
and  ,
,

For every  and
and  , by (3.9), we have
, by (3.9), we have

Therefore by (3.13) and Lemma 3.2, we have

If  then for a sufficiently small
then for a sufficiently small  , we have
, we have  Similar to the above, for every
Similar to the above, for every  , we obtain by (3.10)
, we obtain by (3.10)

If  , choose
, choose  sufficiently large, such that
sufficiently large, such that

By the definition of  , there is an
, there is an  such that, for
such that, for  and
and 

For every  , by (3.8)–(3.10) and (3.13), we have
, by (3.8)–(3.10) and (3.13), we have

which implies that

Finally, we consider the assumption  . By the definition of
. By the definition of  , there is
, there is
 , such that, for
, such that, for  and
and  ,
,

We now show that there is  , such that, for
, such that, for  ,
,  In fact, for
In fact, for 
 and every
and every  ,
,  hence in a similar way, we have
hence in a similar way, we have

which implies that

Theorem 4.2.
Assume that (H ),(H
),(H ), and (H
), and (H ) hold. If
) hold. If  or
or  , then there is a
, then there is a  such that for
such that for  , BVP (4.1) has at least one positive solution.
, BVP (4.1) has at least one positive solution.
Proof.
Let  be given. Define
be given. Define

Then  , where
, where  .
.
For every  , we know that
, we know that  . By the definition of operator
. By the definition of operator  , we obtain
, we obtain

It follows that we can take  such that, for all
such that, for all  and all
and all  ,
,

Fix  . If
. If  , for
, for  , we obtain a sufficiently large
, we obtain a sufficiently large  such that, for
such that, for  ,
,

It follows that, for  and
and  ,
,

For every  , by the definition of
, by the definition of  ,
,  and the definition of Lemma 3.2, there exists a
and the definition of Lemma 3.2, there exists a  such that
such that  and
and  , thus
, thus  . Hence
. Hence

If  there is
there is  , such that, for
, such that, for  and
and  ,
,

where  .
.
For every  , by(3.8)–(3.10) and Lemma 3.2,
, by(3.8)–(3.10) and Lemma 3.2,

which by combining with (4.21) completes the proof.
Example 4.3.
Consider the BVP(3.33) in Example 3.9 with

where  ,
,  is some positive constant,
is some positive constant,  .
.
By calculation,  ,
,  , and
, and  ; let
; let  . Then by Theorem(4.1), for
. Then by Theorem(4.1), for  , the above equation has at least one positive solution.
, the above equation has at least one positive solution.
References
Gai MJ, Shi B, Zhang DC: Boundary value problems for second-order singular functional differential equations. Chinese Annals of Mathematics 2001,23A(6):1-10.
Guo Y, Tian J: Two positive solutions for second-order quasilinear differential equation boundary value problems with sign changing nonlinearities. Journal of Computational and Applied Mathematics 2004,169(2):345-357. 10.1016/j.cam.2003.12.029
Henderson J, Peterson A: Boundary value problems for functional difference equations. Applied Mathematics Letters 1996,9(3):57-61. 10.1016/0893-9659(96)00032-8
Yang SJ, Shi B, Gai MJ: Boundary value problems for functional differential systems. Indian Journal of Pure and Applied Mathematics 2005,36(12):685-705.
Deng X, Shi H: On boundary value problems for second order nonlinear functional difference equations. Acta Applicandae Mathematicae 2009,110(3):1277-1287.
Ntouyas SK, Sficas YG, Tsamatos PCh: Boundary value problems for functional-differential equations. Journal of Mathematical Analysis and Applications 1996,199(1):213-230. 10.1006/jmaa.1996.0137
Wong F-H:Existence of positive solutions for
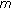 -Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11-17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11-17. 10.1016/S0893-9659(98)00164-5Weng PX, Guo ZH:Existence of positive solutions to BVPs for a nonlinear functional difference equation with
 -Laplacian operator. Acta Mathematica Sinica 2006,49(1):187-194.
-Laplacian operator. Acta Mathematica Sinica 2006,49(1):187-194.Yang SJ, Shi B, Zhang DC:Existence of positive solutions for boundary value problems of nonlinear functional difference equation with
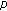 -Laplacian operator. Boundary Value Problems 2007, 2007:-12.
-Laplacian operator. Boundary Value Problems 2007, 2007:-12.Zhao Z: Solutions and Green's functions for some linear second-order three-point boundary value problems. Computers and Mathematics with Applications 2008,56(1):104-113. 10.1016/j.camwa.2007.11.037
Guo DJ, Sun JX, Liu ZL: Functional Methods of Nonlinear Ordinary Differential Equations. Shandong Science and Technology Press, Jinan, China; 1995.
Acknowledgments
The authors would like to thank the editor and the reviewers for their valuable comments and suggestions which helped to significantly improve the paper. This work is supported by Distinguished Expert Science Foundation of Naval Aeronautical and Astronautical University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shujie, Y., Bao, S. Solutions and Green's Functions for Boundary Value Problems of Second-Order Four-Point Functional Difference Equations. Bound Value Probl 2010, 973731 (2010). https://doi.org/10.1155/2010/973731
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/973731
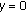 .
. .
.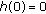 .
. .
. for
for  , then
, then  ;
; for
for  , then
, then 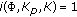 .
.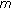 -Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11-17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11-17. 10.1016/S0893-9659(98)00164-5 -Laplacian operator. Acta Mathematica Sinica 2006,49(1):187-194.
-Laplacian operator. Acta Mathematica Sinica 2006,49(1):187-194.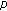 -Laplacian operator. Boundary Value Problems 2007, 2007:-12.
-Laplacian operator. Boundary Value Problems 2007, 2007:-12.