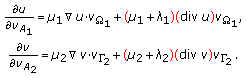Transmission Problem in Thermoelasticity

Abstract

We show that the energy to the thermoelastic transmission problem decays exponentially as time goes to infinity. We also prove the existence, uniqueness, and regularity of the solution to the system.

1. Introduction

In this paper we deal with the theory of thermoelasticity. We consider the following transmission problem between two thermoelastic materials:

(1.1)

(1.2)

(1.3)

(1.4)

We denote by a point of () while stands for the time variable. The displacement in the thermoelasticity parts is denoted by , (, ) and , (, ), , and is the variation of temperature between the actual state and a reference temperature, respectively. , are the thermal conductivity. All the constants of the system are positive. Let us consider an -dimensional body which is configured in ().

The thermoelastic parts are given by and , respectively. The constants are the coupling parameters depending on the material properties. The boundary of is denoted by and the boundary of by . We will consider the boundaries and of class in the rest of this paper. The thermoelastic parts are given by and , respectively, that is (see Figure 1),

(1.5)

We consider for the operators

(1.6)

(1.7)

where , () are the Lamé moduli satisfying .

Figure 1

Domains and and boundaries of the transmission problem.

The initial conditions are given by

(1.8)

(1.9)

The system is subject to the following boundary conditions:

(1.10)

(1.11)

and transmission conditions

(1.12)

(1.13)

The transmission conditions are imposed, that express the continuity of the medium and the equilibrium of the forces acting on it. The discontinuity of the coefficients of the equations corresponds to the fact that the medium consists of two physically different materials.

Since the domain is composed of two different materials, its density is not necessarily a continuous function, and since the stress-strain relation changes from the thermoelastic parts, the corresponding model is not continuous. Taking in consideration this, the mathematical problem that deals with this type of situation is called a transmission problem. From a mathematical point of view, the transmission problem is described by a system of partial differential equations with discontinuous coefficients. The model (1.1)–(1.13) to consider is interesting because we deal with composite materials. From the economical and the strategic point of view, materials are mixed with others in order to get another more convenient material for industry (see [1–3] and references therein). Our purpose in this work is to investigate that the solution of the symmetrical transmission problem decays exponentially as time tends to infinity, no matter how small is the size of the thermoelastic parts. The transmission problem has been of interest to many authors, for instance, in the one-dimensional thermoelastic composite case, we can refer to the papers [4–7]. In the two-, three- or -dimensional, we refer the reader to the papers [8, 9] and references therein. The method used here is based on energy estimates applied to nonlinear problems, and the differential inequality is obtained by exploiting the symmetry of the solutions and applying techniques for the elastic wave equations, which solve the exponential stability produced by the boundary terms in the interface of the material. This methods allow us to find a Lyapunov functional equivalent to the second-order energy for which we have that

(1.14)

In spite of the obvious importance of the subject in applications, there are relatively few mathematical results about general transmission problem for composite materials. For this reason we study this topic here.

This paper is organized as follows. Before describing the main results, in Section 2, we briefly outline the notation and terminology to be used later on and we present some lemmas. In Section 3 we prove the existence and regularity of radially symmetric solutions to the transmission problem. In Section 4 we show the exponential decay of the solutions and we prove the main theorem.

2. Preliminaries

We will use the following standard notation. Let be a domain in . For , are all real valued measurable functions on such that is integrable for and is finite for . The norm will be written as

(2.1)

For a nonnegative integer and , we denote by the Sobolev space of functions in having all derivatives of order belonging to . The norm in is given by . with norm , with norm . We write for the space of -valued functions which are -times continuously differentiable (resp. square integrable) in , where is an interval, is a Banach space, and is a nonnegative integer. We denote by the set of orthogonal real matrices and by the set of matrices in which have determinant 1.

The following results are going to be used several times from now on. The proof can be found in [10].

Lemma 2.1.

Let for or for be arbitrary but fixed. Assume that , , , , , and satisfy

(2.2)

Then the solution , , , and of (1.1)–(1.13) has the form

(2.3)

(2.4)

(2.5)

(2.6)

where , for some functions , , , and .

Lemma 2.2.

One supposes that is a radially symmetric function satisfying . Then there exists a positive constant such that

(2.7)

Moreover one has the following estimate at the boundary:

(2.8)

Remark 2.3.

From (2.3) we have that

(2.9)

The following straightforward calculations are going to be used several times from now on.

• (a) From (1.8) we obtain

  

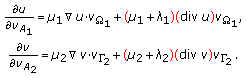  (2.10)

• (b) Using (1.10) and (1.11) we have that

  

  (2.11)

(2.12)

(2.13)

(2.14)

• (c) Using (1.6) we have that

  

  (2.15)

Thus, using (1.10) and (1.11) we have that

(2.16)

Similarly, we obtain

(2.17)

Throughout this paper is a generic constant, not necessarily the same at each occasion (it will change from line to line), which depends in an increasing way on the indicated quantities.

3. Existence and Uniqueness

In this section we establish the existence and uniqueness of solutions to the system (1.1)–(1.13). The proof is based using the standard Galerkin approximation and the elliptic regularity for transmission problem given in [11]. First of all, we define what we will understand for weak solution of the problem (1.1)–(1.13).

We introduce the following spaces:

(3.1)

for and .

Definition 3.1.

One says that is a weak solution of (1.1)–(1.13) if

(3.2)

satisfying the identities

(3.3)

(3.4)

for all , , , and almost every such that

(3.5)

The existence of solutions to the system (1.1)–(1.13) is given in the following theorem.

Theorem 3.2.

One considers the following initial data satisfying

(3.6)

Then there exists only one solution of the system (1.1)–(1.13) satisfying

(3.7)

Moreover, if

(3.8)

verifying the boundary conditions

(3.9)

and the transmission conditions

(3.10)

then the solution satisfies

(3.11)

Proof.

The existence of solutions follows using the standard Galerking approximation.

Faedo-Galerkin Scheme

Given , denote by and the projections on the subspaces

(3.12)

of and , respectively. Let us write

(3.13)

where and satisfy

(3.14)

(3.15)

with

(3.16)

for almost all , where , , , and are the zero vectors in the respective spaces. Recasting exactly the classical Faedo-Galerkin scheme, we get a system of ordinary differential equations in the variables and . According to the standard existence theory for ordinary differential equations there exists a continuous solution of this system, on some interval . The a priori estimates that follow imply that in fact .

Energy Estimates

Multiplying (3.14) by , summing up over , and integrating over we obtain

(3.17)

where

(3.18)

Multiplying (3.15) by , summing up over , and integrating over we obtain

(3.19)

where

(3.20)

Adding (3.17) with (3.19) we obtain

(3.21)

where

(3.22)

Integrating over , , we have that

(3.23)

Thus,

(3.24)

Hence,

(3.25)

In particular,

(3.26)

and it follows that

(3.27)

The system (1.1)–(1.4) is a linear system, and hence the rest of the proof of the existence of weak solution is a standard matter.

The uniqueness follows using the elliptic regularity for the elliptic transmission problem (see [11]).We suppose that there exist two solutions , , and we denote

(3.28)

Taking

(3.29)

we can see that satisfies (1.1)–(1.4). Since , are weak solutions of the system we have that satisfies

(3.30)

Using the elliptic regularity for the elliptic transmission problem we conclude that

(3.31)

Thus satisfies (1.1)–(1.4) in the strong sense. Multiplying (1.1) by , (1.2) by , (1.3) by , and (1.4) by and performing similar calculations as above we obtain , where

(3.32)

which implies that , , , and . The uniqueness follows.

To obtain more regularity, we differentiate the approximate system (1.1)–(1.4); then multiplying the resulting system by and and performing similar calculations as in (3.23) we have that

(3.33)

where

(3.34)

Therefore, we find that

(3.35)

Finally, our conclusion will follow by using the regularity result for the elliptic transmission problem (see [11]).

Remark 3.3.

To obtain higher regularity we introduce the following definition.

Definition 3.4.

One will say that the initial data is -regular () if

(3.36)

where the values of and are given by

(3.37)

verifying the boundary conditions

(3.38)

and the transmission conditions

(3.39)

for . Using the above notation we say that if the initial data is -regular, then we have that the solution satisfies

(3.40)

Using the same arguments as in Theorem 3.2, the result follows.

4. Exponential Stability

In this section we prove the exponential stability. The great difficulty here is to deal with the boundary terms in the interface of the material. This difficulty is solved using an observability result of the elastic wave equations together with the fact that the solution is radially symmetric.

Lemma 4.1.

Let one suppose that the initial data is 3-regular; then the corresponding solution of the system (1.1)–(1.13) satisfies

(4.1)

(4.2)

where with

(4.3)

and .

Proof.

Multiplying (1.1) by , integrating in , and using (2.16) we have that

(4.4)

Multiplying (1.2) by , integrating in , and using (2.17) we have that

(4.5)

Multiplying (1.3) by , integrating in , and using (2.11) we have that

(4.6)

Multiplying (1.4) by , integrating in , using (2.11), and performing similar calculations as above we have that

(4.7)

Adding up (4.4), (4.5), (4.6), and (4.7) and using (1.12) and (1.13) we obtain

(4.8)

where

(4.9)

Thus

(4.10)

In a similar way we obtain (4.2).

Lemma 4.2.

Under the same hypotheses as in Lemma 4.1 one has that the corresponding solution of the system (1.1)–(1.11) satisfies

(4.11)

(4.12)

where , are positive constants and

(4.13)

Proof.

Multiplying (1.1) by , integrating in , and using (1.10) we have that

(4.14)

Then

(4.15)

Hence

(4.16)

Thus

(4.17)

Hence

(4.18)

Therefore

(4.19)

Similarly, multiplying (1.2) by , integrating in , and performing similar calculations as above we obtain

(4.20)

Multiplying (1.3) by and integrating in we have that

(4.21)

Hence

(4.22)

Then

(4.23)

Using (1.10) and (2.9) and performing similar calculations as above we obtain

(4.24)

Replacing (1.1) in the above equation we obtain

(4.25)

On the other hand

(4.26)

Therefore

(4.27)

Multiplying (1.4) by , integrating in , and performing similar calculations as above we obtain

(4.28)

Adding (4.19) with (4.27) we have that

(4.29)

Adding (4.20) with (4.28) we have that

(4.30)

Moreover, by Lemma 2.2, there exist positive constants , such that

(4.31)

Therefore we obtain

(4.32)

Similarly

(4.33)

The result follows.

Lemma 4.3.

Under the same hypotheses of Lemma 4.1 one has that the corresponding solution of the system (1.1)–(1.13) satisfies

(4.34)

with

(4.35)

where , and are positive constants.

Proof.

Multiplying (1.1) by , integrating in , using (2.9), and performing straightforward calculations we have that

(4.36)

Using (1.10) we obtain

(4.37)

Multiplying (1.2) by , integrating in , and performing similar calculations as above we obtain

(4.38)

Multiplying (1.3) by and integrating in , we have that

(4.39)

Performing similar calculations as above we obtain

(4.40)

Multiplying (1.4) by , integrating in , and performing similar calculation as above we obtain

(4.41)

Adding (4.37), (4.38), (4.40), and (4.41), using (1.13), and performing straightforward calculations we obtain

(4.42)

with

(4.43)

Using the Cauchy inequality we have that

(4.44)

and, from trace and interpolation inequalities, we obtain

(4.45)

Similarly

(4.46)

Replacing in the above equation we obtain

(4.47)

The result follows.

We introduce the following integrals:

(4.48)

where

(4.49)

with , where is a ball with center and radius .

Lemma 4.4.

Under the same hypotheses as in Lemma 4.1 one has that the corresponding solution of the system (1.1)–(1.13) satisfies

(4.50)

(4.51)

where , , and are positive constants and , .

Proof.

Using Lemma A.1, taking as above, , , and , we obtain

(4.52)

Applying the hypothesis on and since

(4.53)

we have that

(4.54)

Using (2.8) and the Cauchy-Schwartz inequality in the last term and performing straightforward calculations we obtain

(4.55)

Finally, considering (1.1) and applying the trace theorem we obtain

(4.56)

with ; there exists a positive constant which proves (4.51).

We now introduce the integrals

(4.57)

Lemma 4.5.

With the same hypotheses as in Lemma 4.1, the following equality holds:

(4.58)

Proof.

Differentiating (1.2) in the -variable we have that

(4.59)

Multiplying the above equation by and integrating in we obtain

(4.60)

Hence

(4.61)

On the other hand, using Lemma A.1 for , , , and we obtain

(4.62)

Multiplying (4.61) by and adding with (4.62) we obtain

(4.63)

The result follows.

We introduce the integral

(4.64)

where and are positive constants.

Lemma 4.6.

Under the same hypotheses as in Lemma 4.1 one has that the corresponding solution of the system (1.1)–(1.13) satisfies

(4.65)

Proof.

From (4.11), (4.12), and (4.34), using the Cauchy-Schwartz inequality and performing straightforward calculations we have that

(4.66)

where , , and are positive constants. By Lemma 2.2, there exist positive constants and such that

(4.67)

Then

(4.68)

Hence, taking , , and we obtain

(4.69)

where we have used

(4.70)

Using (1.10), we have that

(4.71)

Thus

(4.72)

where .

We define the functional

(4.73)

where and are positive constants.

Theorem 4.7.

Let us suppose that is a strong solution of the system (1.1)–(1.13). Then there exist positive constants and such that

(4.74)

Proof.

We will assume that the initial data is 3-regular. The conclusion will follow by standard density arguments. Using Lemmas 4.3 and 4.5 and considering boundary conditions, we find that

(4.75)

From (4.1), (4.2), and (4.75) we have that

(4.76)

where

(4.77)

Using the Cauchy inequality, we see that there exist positive constants , such that

(4.78)

Then . Note that for large enough we have that

(4.79)

From the above two inequalities our conclusion follows.

Appendix

We introduce the following functional:

(A1)

where is a symmetric set of .

Lemma A.1.

Let be a radially symmetric set of . Suppose that and . Then for any function satisfying

(A2)

where and are positive constants, one has that

(A3)

where .

Proof.

We consider

(A4)

Moreover

(A5)

Hence

(A6)

On the other hand,

(A7)

Using

(A8)

we obtain

(A9)

Replacing in (A.6) the result follows.