- Research Article
- Open access
- Published:
Degenerate Anisotropic Differential Operators and Applications
Boundary Value Problems volume 2011, Article number: 268032 (2011)
Abstract
The boundary value problems for degenerate anisotropic differential operator equations with variable coefficients are studied. Several conditions for the separability and Fredholmness in Banach-valued  spaces are given. Sharp estimates for resolvent, discreetness of spectrum, and completeness of root elements of the corresponding differential operators are obtained. In the last section, some applications of the main results are given.
spaces are given. Sharp estimates for resolvent, discreetness of spectrum, and completeness of root elements of the corresponding differential operators are obtained. In the last section, some applications of the main results are given.
1. Introduction and Notations
It is well known that many classes of PDEs, pseudo-Des, and integro-DEs can be expressed as differential-operator equations (DOEs). As a result, many authors investigated PDEs as a result of single DOEs. DOEs in  -valued (Hilbert space valued) function spaces have been studied extensively in the literature (see [1–14] and the references therein). Maximal regularity properties for higher-order degenerate anisotropic DOEs with constant coefficients and nondegenerate equations with variable coefficients were studied in [15, 16].
-valued (Hilbert space valued) function spaces have been studied extensively in the literature (see [1–14] and the references therein). Maximal regularity properties for higher-order degenerate anisotropic DOEs with constant coefficients and nondegenerate equations with variable coefficients were studied in [15, 16].
The main aim of the present paper is to discuss the separability properties of BVPs for higher-order degenerate DOEs; that is,

where  ,
,  are weighted functions,
are weighted functions,  and
and  are linear operators in a Banach Space
are linear operators in a Banach Space  . The above DOE is a generalized form of an elliptic equation. In fact, the special case
. The above DOE is a generalized form of an elliptic equation. In fact, the special case  ,
,  reduces (1.1) to elliptic form.
reduces (1.1) to elliptic form.
Note, the principal part of the corresponding differential operator is nonself-adjoint. Nevertheless, the sharp uniform coercive estimate for the resolvent, Fredholmness, discreetness of the spectrum, and completeness of root elements of this operator are established.
We prove that the corresponding differential operator is separable in  ; that is, it has a bounded inverse from
; that is, it has a bounded inverse from  to the anisotropic weighted space
to the anisotropic weighted space  . This fact allows us to derive some significant spectral properties of the differential operator. For the exposition of differential equations with bounded or unbounded operator coefficients in Banach-valued function spaces, we refer the reader to [8, 15–25].
. This fact allows us to derive some significant spectral properties of the differential operator. For the exposition of differential equations with bounded or unbounded operator coefficients in Banach-valued function spaces, we refer the reader to [8, 15–25].
Let  be a positive measurable weighted function on the region
be a positive measurable weighted function on the region  . Let
. Let  denote the space of all strongly measurable
denote the space of all strongly measurable  -valued functions that are defined on
-valued functions that are defined on  with the norm
with the norm

For  , the space
, the space  will be denoted by
will be denoted by  .
.
The weight  we will consider satisfies an
we will consider satisfies an  condition; that is,
condition; that is,  ,
,  if there is a positive constant
if there is a positive constant  such that
such that

for all cubes  .
.
The Banach space  is called a UMD space if the Hilbert operator
is called a UMD space if the Hilbert operator  is bounded in
is bounded in  ,
,  (see, e.g., [26]). UMD spaces include, for example,
(see, e.g., [26]). UMD spaces include, for example,  ,
,  spaces, and Lorentz spaces
spaces, and Lorentz spaces  ,
,  ,
,  .
.
Let  be the set of complex numbers and
be the set of complex numbers and

A linear operator  is said to be
is said to be  -positive in a Banach space
-positive in a Banach space  with bound
with bound  if
if  is dense on
is dense on  and
and

for all  ,
,  is an identity operator in
is an identity operator in  , and
, and  is the space of bounded linear operators in
is the space of bounded linear operators in  . Sometimes
. Sometimes  will be written as
will be written as  and denoted by
and denoted by  . It is known [27, Section 1.15.1] that there exists fractional powers
. It is known [27, Section 1.15.1] that there exists fractional powers  of the sectorial operator
of the sectorial operator  . Let
. Let  denote the space
denote the space  with graphical norm
with graphical norm

Let  and
and  be two Banach spaces. Now,
be two Banach spaces. Now,  ,
,  ,
,  will denote interpolation spaces obtained from
will denote interpolation spaces obtained from  by the
by the  method [27, Section 1.3.1].
method [27, Section 1.3.1].
A set  is called
is called  -bounded (see [3, 25, 26]) if there is a constant
-bounded (see [3, 25, 26]) if there is a constant  such that for all
such that for all  and
and  ,
, 

where  is a sequence of independent symmetric
is a sequence of independent symmetric  -valued random variables on
-valued random variables on  .
.
The smallest  for which the above estimate holds is called an
for which the above estimate holds is called an  -bound of the collection
-bound of the collection  and is denoted by
and is denoted by  .
.
Let  denote the Schwartz class, that is, the space of all
denote the Schwartz class, that is, the space of all  -valued rapidly decreasing smooth functions on
-valued rapidly decreasing smooth functions on  . Let
. Let  be the Fourier transformation. A function
be the Fourier transformation. A function  is called a Fourier multiplier in
is called a Fourier multiplier in  if the map
if the map  ,
,  is well defined and extends to a bounded linear operator in
is well defined and extends to a bounded linear operator in  . The set of all multipliers in
. The set of all multipliers in  will denoted by
will denoted by  .
.
Let

Definition 1.1.
A Banach space  is said to be a space satisfying a multiplier condition if, for any
is said to be a space satisfying a multiplier condition if, for any  , the
, the  -boundedness of the set
-boundedness of the set  implies that
implies that  is a Fourier multiplier in
is a Fourier multiplier in  , that is,
, that is, 
 for any
for any  .
.
Let  be a multiplier function dependent on the parameter
be a multiplier function dependent on the parameter  . The uniform
. The uniform  -boundedness of the set
-boundedness of the set  ; that is,
; that is,

implies that  is a uniform collection of Fourier multipliers.
is a uniform collection of Fourier multipliers.
Definition 1.2.
The  -positive operator
-positive operator  is said to be
is said to be  -positive in a Banach space
-positive in a Banach space  if there exists
if there exists  such that the set
such that the set  is
is  -bounded.
-bounded.
A linear operator  is said to be
is said to be  -positive in
-positive in  uniformly in
uniformly in  if
if  is independent of
is independent of  ,
,  is dense in
is dense in  and
and  for any
for any  ,
,  .
.
The  -positive operator
-positive operator  ,
,  is said to be uniformly
is said to be uniformly  -positive in a Banach space
-positive in a Banach space  if there exists
if there exists  such that the set
such that the set  is uniformly
is uniformly  -bounded; that is,
-bounded; that is,

Let  denote the space of all compact operators from
denote the space of all compact operators from  to
to  . For
. For  , it is denoted by
, it is denoted by  .
.
For two sequences  and
and  of positive numbers, the expression
of positive numbers, the expression  means that there exist positive numbers
means that there exist positive numbers  and
and  such that
such that

Let  denote the space of all compact operators from
denote the space of all compact operators from  to
to  . For
. For  , it is denoted by
, it is denoted by  .
.
Now,  denotes the approximation numbers of operator
denotes the approximation numbers of operator  (see, e.g., [27, Section 1.16.1]). Let
(see, e.g., [27, Section 1.16.1]). Let

Let  and
and  be two Banach spaces and
be two Banach spaces and  continuously and densely embedded into
continuously and densely embedded into  and
and  .
.
We let  denote the space of all functions
denote the space of all functions  possessing generalized derivatives
possessing generalized derivatives  such that
such that  with the norm
with the norm

Let  . Consider the following weighted spaces of functions:
. Consider the following weighted spaces of functions:

2. Background
The embedding theorems play a key role in the perturbation theory of DOEs. For estimating lower order derivatives, we use following embedding theorems from [24].
Theorem A1.
Let  and
and  and suppose that the following conditions are satisfied:
and suppose that the following conditions are satisfied:
(1) is a Banach space satisfying the multiplier condition with respect to
is a Banach space satisfying the multiplier condition with respect to  and
and  ,
,
(2) is an
is an  -positive operator in
-positive operator in  ,
,
(3) and
and  are
are  -tuples of nonnegative integer such that
-tuples of nonnegative integer such that

(4) is a region such that there exists a bounded linear extension operator from
is a region such that there exists a bounded linear extension operator from  to
to  .
.
Then, the embedding  is continuous. Moreover, for all positive number
is continuous. Moreover, for all positive number  and
and  , the following estimate holds
, the following estimate holds

Theorem A2.
Suppose that all conditions of Theorem A1 are satisfied. Moreover, let  ,
,  be a bounded region and
be a bounded region and  . Then, the embedding
. Then, the embedding

is compact.
Let  denote the closure of the linear span of the root vectors of the linear operator
denote the closure of the linear span of the root vectors of the linear operator  .
.
From [18, Theorem 3.4.1], we have the following.
Theorem A3.
Assume that
(1) is an UMD space and
is an UMD space and  is an operator in
is an operator in  ,
,  ,
,
(2) are non overlapping, differentiable arcs in the complex plane starting at the origin. Suppose that each of the
are non overlapping, differentiable arcs in the complex plane starting at the origin. Suppose that each of the  regions into which the planes are divided by these arcs is contained in an angular sector of opening less then
regions into which the planes are divided by these arcs is contained in an angular sector of opening less then  ,
,
(3) is an integer so that the resolvent of
is an integer so that the resolvent of  satisfies the inequality
satisfies the inequality

as  along any of the arcs
along any of the arcs  .
.
Then, the subspace  contains the space
contains the space  .
.
Let

Let

Let  denote the embedding operator
denote the embedding operator 
 .
.
From [15, Theorem 2.8], we have the following.
Theorem A4.
Let  and
and  be two Banach spaces possessing bases. Suppose that
be two Banach spaces possessing bases. Suppose that

Then,

3. Statement of the Problem
Consider the BVPs for the degenerate anisotropic DOE


where

 ,
,  ,
,  are complex numbers,
are complex numbers,  are complex-valued functions on
are complex-valued functions on  ,
,  , and
, and  are linear operators in
are linear operators in  . Moreover,
. Moreover,  and
and  are such that
are such that

A function  and satisfying (3.1) a.e. on
and satisfying (3.1) a.e. on  is said to be solution of the problem (3.1)-(3.2).
is said to be solution of the problem (3.1)-(3.2).
We say the problem (3.1)-(3.2) is  -separable if for all
-separable if for all  , there exists a unique solution
, there exists a unique solution 
 of the problem (3.1)-(3.2) and a positive constant
of the problem (3.1)-(3.2) and a positive constant  depending only
depending only  such that the coercive estimate
such that the coercive estimate

holds.
Let  be a differential operator generated by problem (3.1)-(3.2) with
be a differential operator generated by problem (3.1)-(3.2) with  ; that is,
; that is,

We say the problem (3.1)-(3.2) is Fredholm in  if
if  , where
, where  is a conjugate of
is a conjugate of  .
.
Remark 3.1.
Under the substitutions

the spaces  and
and  are mapped isomorphically onto the weighted spaces
are mapped isomorphically onto the weighted spaces  and
and  , where
, where

Moreover, under the substitution (3.7) the problem (3.1)-(3.2) reduces to the nondegenerate BVP

where

By denoting  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  again by
again by  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , respectively, we get
, respectively, we get

4. BVPs for Partial DOE
Let us first consider the BVP for the anisotropic type DOE with constant coefficients

where

 are boundary conditions defined by (3.2),
are boundary conditions defined by (3.2),  are complex numbers,
are complex numbers,  is a complex parameter, and
is a complex parameter, and  is a linear operator in a Banach space
is a linear operator in a Banach space  . Let
. Let  be the roots of the characteristic equations
be the roots of the characteristic equations

Now, let

By applying the trace theorem [27, Section 1.8.2], we have the following.
Theorem A5.
Let  and
and  be integer numbers,
be integer numbers,  ,
,  ,
,  . Then, for any
. Then, for any  , the transformations
, the transformations  are bounded linear from
are bounded linear from  onto
onto  , and the following inequality holds:
, and the following inequality holds:

Proof.
It is clear that

Then, by applying the trace theorem [27, Section 1.8.2] to the space  , we obtain the assertion.
, we obtain the assertion.
Condition 1.
Assume that the following conditions are satisfied:
(1) is a Banach space satisfying the multiplier condition with respect to
is a Banach space satisfying the multiplier condition with respect to  and the weight function
and the weight function  ,
,  ;
;
(2) is an
is an  -positive operator in
-positive operator in  for
for  ;
;
(3) , and
, and

for  ,
,  .
.
Let  denote the operator in
denote the operator in  generated by BVP (4.1). In [15, Theorem 5.1] the following result is proved.
generated by BVP (4.1). In [15, Theorem 5.1] the following result is proved.
Theorem A6.
Let Condition 1 be satisfied. Then,
-
(a)
the problem (4.1) for
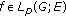 and
and 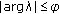 with sufficiently large
with sufficiently large 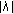 has a unique solution
has a unique solution  that belongs to
that belongs to 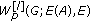 and the following coercive uniform estimate holds:
and the following coercive uniform estimate holds: 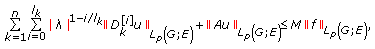 (4.8)
(4.8)
(b)the operator  is
is  -positive in
-positive in  .
.
From Theorems A5 and A6 we have.
Theorem A7.
Suppose that Condition 1 is satisfied. Then, for sufficiently large  with
with  the problem (4.1) has a unique solution
the problem (4.1) has a unique solution  for all
for all  and
and  . Moreover, the following uniform coercive estimate holds:
. Moreover, the following uniform coercive estimate holds:

Consider BVP (3.11). Let  be roots of the characteristic equations
be roots of the characteristic equations

Condition 2.
Suppose the following conditions are satisfied:
(1) and
and

for

(2) is a Banach space satisfying the multiplier condition with respect to
is a Banach space satisfying the multiplier condition with respect to  and the weighted function
and the weighted function  ,
,  .
.
Remark 4.1.
Let  and
and  , where
, where  are real-valued positive functions. Then, Condition 2 is satisfied for
are real-valued positive functions. Then, Condition 2 is satisfied for  .
.
Consider the inhomogenous BVP (3.1)-(3.2); that is,

Lemma 4.2.
Assume that Condition 2 is satisfied and the following hold:
(1) is a uniformly
is a uniformly  -positive operator in
-positive operator in  for
for  , and
, and  are continuous functions on
are continuous functions on  ,
,  ,
,
(2) and
and  for
for  .
.
Then, for all  and for sufficiently large
and for sufficiently large  the following coercive uniform estimate holds:
the following coercive uniform estimate holds:

for the solution of problem (4.13).
Proof.
Let  be regions covering
be regions covering  and let
and let  be a corresponding partition of unity; that is,
be a corresponding partition of unity; that is,  ,
,  and
and  . Now, for
. Now, for  and
and  , we get
, we get

where

here,  and
and  are boundary operators which orders less than
are boundary operators which orders less than  . Freezing the coefficients of (4.15), we have
. Freezing the coefficients of (4.15), we have

where

It is clear that 
 on neighborhoods of
on neighborhoods of  and
and

on neighborhoods of  and
and  on other parts of the domains
on other parts of the domains  , where
, where  are positive constants. Hence, the problems (4.17) are generated locally only on parts of the boundary. Then, by Theorem A7 problem (4.17) has a unique solution
are positive constants. Hence, the problems (4.17) are generated locally only on parts of the boundary. Then, by Theorem A7 problem (4.17) has a unique solution  and for
and for  the following coercive estimate holds:
the following coercive estimate holds:

From the representation of  ,
,  and in view of the boundedness of the coefficients, we get
and in view of the boundedness of the coefficients, we get

Now, applying Theorem A1 and by using the smoothness of the coefficients of (4.16), (4.18) and choosing the diameters of  so small, we see there is an
so small, we see there is an  and
and  such that
such that

Then, using Theorem A5 and using the smoothness of the coefficients of (4.16), (4.18), we get

Now, using Theorem A1, we get that there is an  and
and  such that
such that

where

Using the above estimates, we get

Consequently, from (4.22)–(4.26), we have

Choosing  from the above inequality, we obtain
from the above inequality, we obtain

Then, by using the equality 
 and the above estimates, we get (4.14).
and the above estimates, we get (4.14).
Condition 3.
Suppose that part (1.1) of Condition 1 is satisfied and that  is a Banach space satisfying the multiplier condition with respect to
is a Banach space satisfying the multiplier condition with respect to  and the weighted function
and the weighted function  ,
,  ,
,  .
.
Consider the problem (3.11). Reasoning as in the proof of Lemma 4.2, we obtain.
Proposition 4.3.
Assume Condition 3 hold and suppose that
(1) is a uniformly
is a uniformly  -positive operator in
-positive operator in  for
for  , and that
, and that  are continuous functions on
are continuous functions on  ,
,  ,
,
(2) and
and  for
for  .
.
Then, for all  and for sufficiently large
and for sufficiently large  , the following coercive uniform estimate holds
, the following coercive uniform estimate holds

for the solution of problem (3.11).
Let  denote the operator generated by problem (3.11) for
denote the operator generated by problem (3.11) for  ; that is,
; that is,

Theorem 4.4.
Assume that Condition 3 is satisfied and that the following hold:
(1) is a uniformly
is a uniformly  -positive operator in
-positive operator in  , and
, and  are continuous functions on
are continuous functions on  ,
,
(2) , and
, and  for
for  .
.
Then, problem (3.11) has a unique solution 
 for
for  and
and  with large enough
with large enough  . Moreover, the following coercive uniform estimate holds:
. Moreover, the following coercive uniform estimate holds:

Proof.
By Proposition 4.3 for  , we have
, we have

It is clear that

Hence, by using the definition of  and applying Theorem A1, we obtain
and applying Theorem A1, we obtain

From the above estimate, we have

The estimate (4.35) implies that problem (3.11) has a unique solution and that the operator  has a bounded inverse in its rank space. We need to show that this rank space coincides with the space
has a bounded inverse in its rank space. We need to show that this rank space coincides with the space  ; that is, we have to show that for all
; that is, we have to show that for all  , there is a unique solution of the problem (3.11). We consider the smooth functions
, there is a unique solution of the problem (3.11). We consider the smooth functions  with respect to a partition of unity
with respect to a partition of unity  on the region
on the region  that equals one on
that equals one on  , where supp
, where supp  and
and  . Let us construct for all
. Let us construct for all  the functions
the functions  that are defined on the regions
that are defined on the regions  and satisfying problem (3.11). The problem (3.11) can be expressed as
and satisfying problem (3.11). The problem (3.11) can be expressed as

Consider operators  in
in  that are generated by the BVPs (4.17); that is,
that are generated by the BVPs (4.17); that is,

By virtue of Theorem A6, the operators  have inverses
have inverses  for
for  and for sufficiently large
and for sufficiently large  . Moreover, the operators
. Moreover, the operators  are bounded from
are bounded from  to
to  , and for all
, and for all  , we have
, we have

Extending  to zero outside of
to zero outside of  in the equalities (4.36), and using the substitutions
in the equalities (4.36), and using the substitutions  , we obtain the operator equations
, we obtain the operator equations

where  are bounded linear operators in
are bounded linear operators in  defined by
defined by

In fact, because of the smoothness of the coefficients of the expression  and from the estimate (4.38), for
and from the estimate (4.38), for  with sufficiently large
with sufficiently large  , there is a sufficiently small
, there is a sufficiently small  such that
such that

Moreover, from assumption (2.2) of Theorem 4.4 and Theorem A1 for  , there is a constant
, there is a constant  such that
such that

Hence, for  with sufficiently large
with sufficiently large  , there is a
, there is a  such that
such that  . Consequently, (4.39) for all
. Consequently, (4.39) for all  have a unique solution
have a unique solution  . Moreover,
. Moreover,

Thus,  are bounded linear operators from
are bounded linear operators from  to
to  . Thus, the functions
. Thus, the functions

are solutions of (4.38). Consider the following linear operator  in
in  defined by
defined by

It is clear from the constructions  and from the estimate (4.39) that the operators
and from the estimate (4.39) that the operators  are bounded linear from
are bounded linear from  to
to  , and for
, and for  with sufficiently large
with sufficiently large  , we have
, we have

Therefore,  is a bounded linear operator in
is a bounded linear operator in  . Since the operators
. Since the operators  coincide with the inverse of the operator
coincide with the inverse of the operator  in
in  , then acting on
, then acting on  to
to  gives
gives

where  are bounded linear operators defined by
are bounded linear operators defined by

Indeed, from Theorem A1 and estimate (4.46) and from the expression  , we obtain that the operators
, we obtain that the operators  are bounded linear from
are bounded linear from  to
to  , and for
, and for  with sufficiently large
with sufficiently large  , there is an
, there is an  such that
such that  . Therefore, there exists a bounded linear invertible operator
. Therefore, there exists a bounded linear invertible operator  ; that is, we infer for all
; that is, we infer for all  that the BVP (3.11) has a unique solution
that the BVP (3.11) has a unique solution

Result 1.
Theorem 4.4 implies that the resolvent  satisfies the following anisotropic type sharp estimate:
satisfies the following anisotropic type sharp estimate:

for  ,
,  .
.
Let  denote the operator generated by BVP (3.1)-(3.2). From Theorem 4.4 and Remark 3.1, we get the following.
denote the operator generated by BVP (3.1)-(3.2). From Theorem 4.4 and Remark 3.1, we get the following.
Result 2.
Assume all the conditions of Theorem 4.4 hold. Then,
(a)the problem (3.1)-(3.2) for  ,
,  and for sufficiently large
and for sufficiently large  has a unique solution
has a unique solution 
 , and the following coercive uniform estimate holds
, and the following coercive uniform estimate holds

(b)if  , then the operator
, then the operator  is Fredholm from
is Fredholm from  into
into  .
.
Example 4.5.
Now, let us consider a special case of (3.1)-(3.2). Let  ,
,  and
and  ,
,  ,
,  and
and  ; that is, consider the problem
; that is, consider the problem

where

Theorem 4.4 implies that for each  , problem (4.52) has a unique solution
, problem (4.52) has a unique solution  satisfying the following coercive estimate:
satisfying the following coercive estimate:

Example 4.6.
Let  and
and  , where
, where  are positive continuous function on
are positive continuous function on  ,
,  and
and  is a diagonal matrix-function with continuous components
is a diagonal matrix-function with continuous components  .
.
Then, we obtain the separability of the following BVPs for the system of anisotropic PDEs with varying coefficients:

in the vector-valued space  .
.
5. The Spectral Properties of Anisotropic Differential Operators
Consider the following degenerated BVP:

where

Consider the operator  generated by problem (5.1).
generated by problem (5.1).
Theorem 5.1.
Let all the conditions of Theorem 4.4 hold for  and
and  . Then, the operator
. Then, the operator  is Fredholm from
is Fredholm from  into
into  .
.
Proof.
Theorem 4.4 implies that the operator  for sufficiently large
for sufficiently large  has a bounded inverse
has a bounded inverse  from
from  to
to  ; that is, the operator
; that is, the operator  is Fredholm from
is Fredholm from  into
into  . Then, from Theorem A2 and the perturbation theory of linear operators, we obtain that the operator
. Then, from Theorem A2 and the perturbation theory of linear operators, we obtain that the operator  is Fredholm from
is Fredholm from  into
into  .
.
Theorem 5.2.
Suppose that all the conditions of Theorem 5.1 are satisfied with  . Assume that
. Assume that  is a Banach space with a basis and
is a Banach space with a basis and

Then,
(a)for a sufficiently large positive

(b)the system of root functions of the differential operator  is complete in
is complete in  .
.
Proof.
Let  denote the embedding operator from
denote the embedding operator from  to
to  . From Result 2, there exists a resolvent operator
. From Result 2, there exists a resolvent operator  which is bounded from
which is bounded from  to
to  . Moreover, from Theorem A4 and Remark 3.1, we get that the embedding operator
. Moreover, from Theorem A4 and Remark 3.1, we get that the embedding operator

is compact and

It is clear that

Hence, from relations (5.6) and (5.7), we obtain (5.4). Now, Result 1 implies that the operator 
 is positive in
is positive in  and
and

Then, from (4.52) and (5.6), we obtain assertion (b).
Consider now the operator  in
in  generated by the nondegenerate BVP obtained from (5.1) under the mapping (3.7); that is,
generated by the nondegenerate BVP obtained from (5.1) under the mapping (3.7); that is,

From Theorem 5.2 and Remark 3.1, we get the following.
Result 3.
Let all the conditions of Theorem 5.1 hold. Then, the operator  is Fredholm from
is Fredholm from  into
into  .
.
Result 4.
Then,
(a)for a sufficiently large positive 

(b)the system of root functions of the differential operator  is complete in
is complete in  .
.
6. BVPs for Degenerate Quasielliptic PDE
In this section, maximal regularity properties of degenerate anisotropic differential equations are studied. Maximal regularity properties for PDEs have been studied, for example, in [3] for smooth domains and in [28] for nonsmooth domains.
Consider the BVP

where  ,
,  ,
,  are complex number,
are complex number,  and
and

Let  ,
,  . Now,
. Now,  will denote the space of all
will denote the space of all  -summable scalar-valued functions with mixed norm (see, e.g., [29, Section 1, page 6]), that is, the space of all measurable functions
-summable scalar-valued functions with mixed norm (see, e.g., [29, Section 1, page 6]), that is, the space of all measurable functions  defined on
defined on  , for which
, for which

Analogously,  denotes the Sobolev space with corresponding mixed norm.
denotes the Sobolev space with corresponding mixed norm.
Let 
 ,
,  ,
,  denote the roots of the equations
denote the roots of the equations

Let  denote the operator generated by BVP (6.1). Let
denote the operator generated by BVP (6.1). Let

Theorem 6.1.
Let the following conditions be satisfied:
(1) for each
for each  and
and  for each
for each  with
with  ,
,  and
and  ,
,  ,
,
(2) for each
for each  ,
,  ,
,  ,
,  ,
,  ,
,
(3)for  ,
,  ,
,  ,
,  ,
,  let
let

(4)for each  , the local BVPs in local coordinates corresponding to
, the local BVPs in local coordinates corresponding to 

has a unique solution  for all
for all  and for
and for  with
with  ,
,
(5) ,
,  and
and

Then,
(a)the following coercive estimate

holds for the solution  of problem (6.1),
of problem (6.1),
(b)for  and for sufficiently large
and for sufficiently large  , there exists a resolvent
, there exists a resolvent  and
and

(c)the problem (6.1) for  is Fredholm in
is Fredholm in  ,
,
(d)the relation with 

holds,
(e)for  the system of root functions of the BVP (6.1) is complete in
the system of root functions of the BVP (6.1) is complete in  .
.
Proof.
Let  . Then, from [3, Theorem 3.6], part (1.1) of Condition 1 is satisfied. Consider the operator
. Then, from [3, Theorem 3.6], part (1.1) of Condition 1 is satisfied. Consider the operator  which is defined by
which is defined by

For  , we also consider operators
, we also consider operators

The problem (6.1) can be rewritten as the form of (3.1)-(3.2), where  and
and  are functions with values in
are functions with values in  . From [3, Theorem 8.2] problem
. From [3, Theorem 8.2] problem

has a unique solution for  and arg
and arg  ,
,  . Moreover, the operator
. Moreover, the operator  , generated by (5.8) is
, generated by (5.8) is  -positive in
-positive in  ; that is, part (2.2) of Condition 1 holds. From (2.2), (3.7), and by [29, Section 18], we have
; that is, part (2.2) of Condition 1 holds. From (2.2), (3.7), and by [29, Section 18], we have

that is, all the conditions of Theorem 5.2 and Result 4 are fulfilled. As a result, we obtain assertion (a) and (b) of the theorem. Also, it is known (e.g., [27, Theorem 3.2.5, Section 4.10]) that the embedding  is compact and
is compact and

Then, Results 3 and 4 imply assertions (c), (d), (e).
7. Boundary Value Problems for Infinite Systems of Degenerate PDE
Consider the infinity systems of BVP for the degenerate anisotropic PDE

where  ,
,  are complex-valued functions,
are complex-valued functions,  ,
,  are complex numbers. Let
are complex numbers. Let

Let  denote the operator in
denote the operator in  generated by problem (7.1). Let
generated by problem (7.1). Let

Theorem 7.1.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
,  such that
such that

Then,
(a)for all  , for
, for  and sufficiently large
and sufficiently large  , the problem (7.1) has a unique solution
, the problem (7.1) has a unique solution  that belongs to the space
that belongs to the space  and the following coercive estimate holds:
and the following coercive estimate holds:

(b)there exists a resolvent  of the operator
of the operator  and
and

(c)for  , the system of root functions of the BVP (7.1) is complete in
, the system of root functions of the BVP (7.1) is complete in  .
.
Proof.
Let  ,
,  and
and  be infinite matrices such that
be infinite matrices such that

It is clear that the operator  is
is  -positive in
-positive in  . The problem (7.1) can be rewritten in the form (1.1). From Theorem 4.4, we obtain that problem (7.1) has a unique solution
. The problem (7.1) can be rewritten in the form (1.1). From Theorem 4.4, we obtain that problem (7.1) has a unique solution 
 for all
for all  and
and

From the above estimate, we obtain assertions (a) and (b). The assertion (c) is obtained from Result 4.
References
Agranovich MS:Spectral problems in Lipschitz domains for strongly elliptic systems in the Banach spaces
 and
and 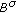 . Functional Analysis and Its Applications 2008, 42(4):249-267. 10.1007/s10688-008-0039-x
. Functional Analysis and Its Applications 2008, 42(4):249-267. 10.1007/s10688-008-0039-xAshyralyev A: On well-posedness of the nonlocal boundary value problems for elliptic equations. Numerical Functional Analysis and Optimization 2003, 24(1-2):1-15. 10.1081/NFA-120020240
Denk R, Hieber M, Prüss J: R-Boundedness, Fourier Multipliers and Problems of Elliptic and Parabolic Type, Mem. Amer. Math. Soc.. American Mathematical Society; 2003.
Favini A, Shakhmurov V, Yakubov Y: Regular boundary value problems for complete second order elliptic differential-operator equations in UMD Banach spaces. Semigroup Forum 2009, 79(1):22-54. 10.1007/s00233-009-9138-0
Gorbachuk VI, Gorbachuk ML: Boundary Value Problems for Differential-Operator Equations. "Naukova Dumka", Kiev, Ukraine; 1984:284.
Goldstein JA: Semigroups of Linear Operators and Applications, Oxford Mathematical Monographs. The Clarendon Press/Oxford University Press, New York, NY, USA; 1985:x+245.
Lions J-L, Magenes E: Nonhomogenous Boundary Value Problems. Mir, Moscow, Russia; 1971.
Shklyar AYa: Complete Second Order Linear Differential Equations in Hilbert Spaces, Operator Theory: Advances and Applications. Volume 92. Birkhäuser, Basel, Switzerland; 1997:xii+219.
Shakhmurov VB: Nonlinear abstract boundary-value problems in vector-valued function spaces and applications. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(3):745-762. 10.1016/j.na.2006.06.027
Shakhmurov VB: Theorems on the embedding of abstract function spaces and their applications. Matematicheskiĭ Sbornik. Novaya Seriya 1987, 134(176)(2):260-273.
Shakhmurov VB: Embedding theorems and their applications to degenerate equations. Differentsial'nye Uravneniya 1988, 24(4):672-682.
Yakubov S: Completeness of Root Functions of Regular Differential Operators, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 71. Longman Scientific & Technical, Harlow, UK; 1994:x+245.
Yakubov S: A nonlocal boundary value problem for elliptic differential-operator equations and applications. Integral Equations and Operator Theory 1999, 35(4):485-506. 10.1007/BF01228044
Yakubov S, Yakubov Y: Differential-Operator Equations: Ordinary and Partial Differential Equations, Chapman & Hall/CRC Monographs and Surveys in Pure and Applied Mathematics. Volume 103. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2000:xxvi+541.
Agarwal RP, Bohner R, Shakhmurov VB: Maximal regular boundary value problems in Banach-valued weighted spaces. Boundary Value Problems 2005, 2005(1):9-42. 10.1155/BVP.2005.9
Shakhmurov VB: Separable anisotropic differential operators and applications. Journal of Mathematical Analysis and Applications 2007, 327(2):1182-1201. 10.1016/j.jmaa.2006.05.007
Amann H: Operator-valued Fourier multipliers, vector-valued Besov spaces, and applications. Mathematische Nachrichten 1997, 186: 5-56.
Amann H: Linear and Quasi-Linear Equations. Birkhauser; 1995.
Krein SG: Linear Differential Equations in Banach Space. American Mathematical Society, Providence, RI, USA; 1971.
Lunardi A: Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progress in Nonlinear Differential Equations and their Applications, 16. Birkhäuser, Basel, Switzerland; 1995:xviii+424.
Orlov VP: Regular degenerate differential operators of arbitrary order with unbounded operators coefficients. Proceedings of Voronej State University 1974, 2: 33-41.
Sobolevskiĭ PE: Inequalities coerciveness for abstract parabolic equations. Doklady Akademii Nauk SSSR 1964, 57: 27-40.
Shakhmurov VB: Coercive boundary value problems for regular degenerate differential-operator equations. Journal of Mathematical Analysis and Applications 2004, 292(2):605-620. 10.1016/j.jmaa.2003.12.032
Shakhmurov VB: Degenerate differential operators with parameters. Abstract and Applied Analysis 2007, 2007:-27.
Weis Lutz:Operator-valued Fourier multiplier theorems and maximal
 -regularity. Mathematische Annalen 2001, 319(4):735-758. 10.1007/PL00004457
-regularity. Mathematische Annalen 2001, 319(4):735-758. 10.1007/PL00004457Burkholder DL: A geometric condition that implies the existence of certain singular integrals of Banach-space-valued functions. Proceedings of the Conference on Harmonic Analysis in Honor of Antoni Zygmund, Vol. I, II, 1981, Chicago, Ill, USA, Wadsworth Math. Ser. 270-286.
Triebel H: Interpolation Theory, Function Spaces, Differential Operators, North-Holland Mathematical Library. Volume 18. North-Holland, Amsterdam, The Netherlands; 1978:528.
Grisvard P: Elliptic Problems in Non Smooth Domains. Pitman; 1985.
Besov OV, Ilin VP, Nikolskii SM: Integral Representations of Functions and Embedding Theorems. Wiley, New York, NY, USA; 1978.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R., O'Regan, D. & Shakhmurov, V. Degenerate Anisotropic Differential Operators and Applications. Bound Value Probl 2011, 268032 (2011). https://doi.org/10.1155/2011/268032
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/268032
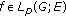 and
and 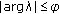 with sufficiently large
with sufficiently large 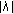 has a unique solution
has a unique solution  that belongs to
that belongs to 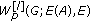 and the following coercive uniform estimate holds:
and the following coercive uniform estimate holds: 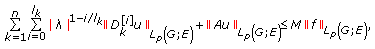
 and
and  . Functional Analysis and Its Applications 2008, 42(4):249-267. 10.1007/s10688-008-0039-x
. Functional Analysis and Its Applications 2008, 42(4):249-267. 10.1007/s10688-008-0039-x -regularity. Mathematische Annalen 2001, 319(4):735-758. 10.1007/PL00004457
-regularity. Mathematische Annalen 2001, 319(4):735-758. 10.1007/PL00004457