- Research Article
- Open access
- Published:
Existence of Positive Solutions of Fourth-Order Problems with Integral Boundary Conditions
Boundary Value Problems volume 2011, Article number: 297578 (2011)
Abstract
We study the existence of positive solutions of the following fourth-order boundary value problem with integral boundary conditions,  ,
,  ,
,  ,
,  ,
,  ,
,  , where
, where  is continuous,
is continuous,  are nonnegative. The proof of our main result is based upon the Krein-Rutman theorem and the global bifurcation techniques.
are nonnegative. The proof of our main result is based upon the Krein-Rutman theorem and the global bifurcation techniques.
1. Introduction
The deformations of an elastic beam in an equilibrium state, whose both ends are simple supported, can be described by the fourth-order boundary value problem


where  is continuous; see Gupta [1, 2]. In the past twenty more years, the existence of solutions and positive solutions of these kinds of problems and the Lidstone problem has been extensively studied; see [3–9] and the references therein. In [3], Ma was concerned with the existence of positive solutions of (1.1) and (1.2) under the assumptions:
is continuous; see Gupta [1, 2]. In the past twenty more years, the existence of solutions and positive solutions of these kinds of problems and the Lidstone problem has been extensively studied; see [3–9] and the references therein. In [3], Ma was concerned with the existence of positive solutions of (1.1) and (1.2) under the assumptions:
(H1)  is continuous and there exist constants
is continuous and there exist constants  , with
, with  such that
such that

uniformly for  , and
, and

uniformly for  , where
, where  ;
;
(H2)  for
for  and
and  ;
;
(H3) there exist constants  satisfying
satisfying  and
and

Ma proved the following.
Theorem A (see [3, Theorem  ]).
]).
Let (H1), (H2), and (H3) hold. Assume that either

or

where  denotes the first generalized eigenvalue of the generalized eigenvalue problem
denotes the first generalized eigenvalue of the generalized eigenvalue problem

Then (1.1) and (1.2) have at least one positive solution.
At the same time, we notice that a class of boundary value problems with integral boundary conditions appeared in heat conduction, chemical engineering underground water flow, thermoelasticity, and plasma physics. Such a kind of problems include two-point, three-point, multipoint and nonlocal boundary value problems as special cases and attracting the attention of a few readers; see [10–13] and the references therein. For example, In particular, Zhang and Ge [10] used Guo-Krasnoselskii fixed-point theorem to study existence and nonexistence of positive solutions of the following fourth-order boundary value problem with integral boundary conditions:

where  may be singular at
may be singular at  and (or)
and (or)  ;
;  is continuous, and
is continuous, and  are nonnegative.
are nonnegative.
Motivated by [3, 10], in this paper, we consider the existence of positive solutions of the following fourth-order boundary value problem with integral boundary conditions:

under the assumption
(H4)  are nonnegative, and
are nonnegative, and  . The main result of this paper is the following.
. The main result of this paper is the following.
Theorem 1.1.
Let (H1), (H2), (H3), and (H4) hold. Assume that either

or

where



Then (1.9) has at least one positive solution.
Remark 1.2.
Theorem 1.1 generalizes [3, Theorem  ] where the special case
] where the special case  and
and  was treated.
was treated.
Remark 1.3.
Zhang and Ge [10] proved existence and nonexistence of positive solutions via Guo-Krasnoselskii fixed-point theorem under some conditions which do not involve the eigenvalues of (1.12)–(1.14). While our Theorem 1.1 is established under (1.10) or (1.11) which is related to the eigenvalues of (1.12)–(1.14). Moreover, (1.10) and (1.11) are optimal. Let us consider the problem


In this case,  and the corresponding eigenfunction is
and the corresponding eigenfunction is  . However, (1.15) and (1.16) has no positive solution. (In fact, suppose on the contrary that (1.15) and (1.16) has a positive solution
. However, (1.15) and (1.16) has no positive solution. (In fact, suppose on the contrary that (1.15) and (1.16) has a positive solution  . Multiplying (1.15) with
. Multiplying (1.15) with  and integrating from
and integrating from  to
to  , we get a desired contradiction!).
, we get a desired contradiction!).
Suppose that  is a real Banach space with norm
is a real Banach space with norm  . Let
. Let  be a cone in
be a cone in  . A nonlinear mapping
. A nonlinear mapping  is said to be positive if
is said to be positive if  . It is said to be
. It is said to be  -completely continuous if
-completely continuous if  is continuous and maps bounded subsets of
is continuous and maps bounded subsets of  to precompact subset of
to precompact subset of  . Finally, a positive linear operator
. Finally, a positive linear operator  on
on  is said to be a linear minorant for
is said to be a linear minorant for  if
if  for
for  . If
. If  is a continuous linear operator on
is a continuous linear operator on  , denote
, denote  the spectral radius of
the spectral radius of  . Define
. Define

The following lemma will play a very important role in the proof of our main results, which is essentially a consequence of Dancer [14, Theorem  ].
].
Lemma 1.4.
Assume that
-
(i)
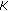 has nonempty interior and
has nonempty interior and  ;
; -
(ii)
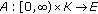 is
is 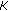 -completely continuous and positive,
-completely continuous and positive, 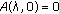 for
for 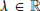 ,
, 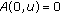 for
for 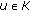 and
and 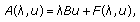 (1.18)
(1.18)
where  is a strongly positive linear compact operator on
is a strongly positive linear compact operator on  with the spectral radius
with the spectral radius  ,
,  satisfies
satisfies  as
as  locally uniformly in
locally uniformly in  .
.
Then there exists an unbounded connected subset  of
of

such that  .
.
Moreover, if  has a linear minorant
has a linear minorant  and there exists a
and there exists a

such that  and
and  , then
, then  can be chosen in
can be chosen in

Proof.
Since  is a strongly positive compact endomorphism of
is a strongly positive compact endomorphism of  and
and  has nonempty interior, we have from Amann [15, Theorem
has nonempty interior, we have from Amann [15, Theorem  ] that the set
] that the set  in [14, Theorem
in [14, Theorem  ] reduces to a single point
] reduces to a single point  . Now the desired result is a consequence of Dancer [14, Theorem
. Now the desired result is a consequence of Dancer [14, Theorem  ].
].
The rest of the paper is arranged as follows. In Section 2, we state and prove some preliminary results about the spectrum of (1.12)–(1.14). Finally, in Section 3, we proved our main result.
2. Generalized Eigenvalues
Lemma 2.1 (see [10]).
Assume that (H4) holds. Then for any  , the boundary value problem
, the boundary value problem

has a unique solution  which is given by
which is given by

where

Lemma 2.2 (see [10]).
Assume that (H4) holds. Then for any  , the boundary value problem
, the boundary value problem

has a unique solution  which is given by
which is given by

where

Lemma 2.3 (see [10]).
Assume that (H4) holds. Then one has

Let
(H5)  be two given constants with
be two given constants with  .
.
Definition 2.4.
One says that
 is a generalized eigenvalue of linear problem
is a generalized eigenvalue of linear problem


if (2.8) and (2.9) have nontrivial solutions.
Let

Let  with the norm
with the norm  . Let
. Let  with the norm
with the norm  .
.
Let

For  , from Lemma 2.1, it follows that
, from Lemma 2.1, it follows that

By simple calculations, we have

Combining this with (H4), we conclude that

This together with (2.12) and the fact that  imply that
imply that

Since  , we may define the norm of
, we may define the norm of  by
by

We claim that  is a Banach space.
is a Banach space.
In fact, let  be a Cauchy sequence, that is,
be a Cauchy sequence, that is,  as
as  . From the definition of
. From the definition of  , it follows that
, it follows that

where  is a normal in
is a normal in  defined by
defined by  . Thus,
. Thus,

By the completeness of  , there exists
, there exists  , such that
, such that

From the fact that  , we have that for arbitrary
, we have that for arbitrary  , there exists
, there exists  , such that
, such that

and subsequently,

Fixed  and let
and let  , we get
, we get

This is,

Therefore,  is a Banach space.
is a Banach space.
Let

Then the cone  is normal and nonempty interior
is normal and nonempty interior  and
and  .
.
In fact, for any  , it follows from the definition of
, it follows from the definition of  that
that
(1) there exist real number  , such that
, such that

(2)  ,
,  .
.
From  and (H4), we obtain that
and (H4), we obtain that  for some
for some  . Moreover,
. Moreover,

and subsequently,

for some  . We may take
. We may take  satisfying
satisfying

Now, let us define

Then  , and
, and

Thus,  . Obviously,
. Obviously,  .
.
Lemma 2.5.
Assume that  holds. Then for any
holds. Then for any  , one has
, one has

Proof.
In fact, for  , we have that
, we have that

From  , we have that
, we have that  , and so
, and so  , and accordingly
, and accordingly  .
.
We have from the fact that  ,
,  , that
, that

which implies that  , and consequently
, and consequently  .
.
For  , define a linear operator
, define a linear operator  by
by

Theorem 2.6.
Assume that (H4) and (H5) hold. Let  be the spectral radius of
be the spectral radius of  . Then (2.8) and (2.9) has an algebraically simple eigenvalue,
. Then (2.8) and (2.9) has an algebraically simple eigenvalue, 
 , with a positive eigenfunction
, with a positive eigenfunction  . Moreover, there is no other eigenvalue with a positive eigenfunction.
. Moreover, there is no other eigenvalue with a positive eigenfunction.
Remark 2.7.
If  , then
, then  can be explicitly given by
can be explicitly given by

and the corresponding eigenfunction  .
.
Proof of Theorem 2.6.
From Lemma 2.2, it is easy to check that (2.8) and (2.9) is equivalent to the integral equation

We claim that  .
.
In fact, for  , we have that
, we have that

Since

and for some constant  , it concludes that
, it concludes that

Hence,

where  , it follows that
, it follows that  , and accordingly
, and accordingly  .
.
If  , then
, then  on
on  , and accordingly
, and accordingly

Thus  , and accordingly
, and accordingly  .
.
Now, since  , and
, and  is compactly embedded in
is compactly embedded in  , we have that
, we have that  is compact.
is compact.
Next, we show that  is positive.
is positive.
For  , if
, if  , from Lemma 2.3, we have
, from Lemma 2.3, we have

Combining this with (2.39), there exist  such that
such that

For  , if
, if  , applying a similar proof process of (2.43), we have
, applying a similar proof process of (2.43), we have

Combining this with (2.39), there exist  such that
such that

This together with (2.9) and (H4) imply  on
on  .
.
Therefore, it follows from (2.43) and (2.45) that  .
.
Now, by the Krein-Rutman theorem ([16, Theorem  C]; [17, Theorem
C]; [17, Theorem  ]),
]),  has an algebraically simple eigenvalue
has an algebraically simple eigenvalue  with an eigenfunction
with an eigenfunction  . Moreover, there is no other eigenvalue with a positive eigenfunction. Correspondingly,
. Moreover, there is no other eigenvalue with a positive eigenfunction. Correspondingly,  with a positive eigenfunction of
with a positive eigenfunction of  , is a simple eigenvalue of (2.8) and (2.9). Moreover, for (2.8) and (2.9), there is no other eigenvalue with a positive eigenfunction.
, is a simple eigenvalue of (2.8) and (2.9). Moreover, for (2.8) and (2.9), there is no other eigenvalue with a positive eigenfunction.
3. The Proof of the Main Result
Before proving Theorem 1.1, we denote  by setting
by setting

where

It is easy to check that  is compact.
is compact.
Let  be such that
be such that

Obviously,( )impliesthat
)impliesthat


Let

then  is nondecreasing and
is nondecreasing and

Let us consider

as a bifurcation problem from the trivial solution  . It is to easy to check that (3.8) can be converted to the equivalent equation
. It is to easy to check that (3.8) can be converted to the equivalent equation

From the proof process of Theorem 2.6, the operator  ,
,

is compact and strongly positive. Define  by
by

then we have from (3.4) and Lemma 2.5 that

locally uniformly in  . From
. From and Theorem 2.6 (with obvious changes), it follows that if
and Theorem 2.6 (with obvious changes), it follows that if  is a nontrivial solution of (3.8) with
is a nontrivial solution of (3.8) with  , then
, then  . Combining this with Lemma 1.4, we conclude that there exists an unbounded connected subset
. Combining this with Lemma 1.4, we conclude that there exists an unbounded connected subset  of the set
of the set

such that  .
.
Proof of Theorem 1.1.
It is clear that any solution of the form  yields a solution
yields a solution  of (1.9). We will show that
of (1.9). We will show that  crosses the hyperplane
crosses the hyperplane  . To do this, it is enough to show that
. To do this, it is enough to show that  joins
joins  to
to  . Let
. Let  satisfy
satisfy

we note that  for all
for all  since
since  is the only solution of (3.8) for
is the only solution of (3.8) for  and
and  .
.
Case 1 ( ).
).
In this case, we show that

We divide the proof into two steps.
Step 1.
We show that if there exists a constant number  such that
such that

then  joins
joins  to
to  .
.
From (3.16), we have that  . We divide the equation
. We divide the equation

by  and set
and set  . Since
. Since  is bounded in
is bounded in  , choosing a subsequence and relabeling if necessary, we see that
, choosing a subsequence and relabeling if necessary, we see that  for some
for some  with
with  . Moreover, we have from (3.7) and Lemma 2.5 that
. Moreover, we have from (3.7) and Lemma 2.5 that

Since  Thus,
Thus,

where  , again choosing a subsequence and relabeling if necessary. Thus,
, again choosing a subsequence and relabeling if necessary. Thus,

This together with Theorem 2.6 imply that  . Therefore,
. Therefore,  joins
joins  to
to  .
.
Step 2.
We show that there exists a constant  be such that
be such that  for all
for all  .
.
By Lemma 1.4, we only need to show that  has a linear minorant
has a linear minorant  and there exists a
and there exists a  such that
such that  and
and  .
.
By ,there exist constants
,there exist constants  satisfying
satisfying  and
and

For  , let
, let

then  is a linear minorant of
is a linear minorant of  . Moreover,
. Moreover,

where

Combining this with (2.39), we conclude that  , here,
, here,  . Therefore, we have that from Lemma 1.4 that
. Therefore, we have that from Lemma 1.4 that  .
.
Case 2 ( ).
).
In this case, if  such that
such that

and  then
then

and, moreover,  .
.
Assume that there exists  , such that for all
, such that for all  ,
,

Applying a similar argument to that used in Step 1 of Case 1, after taking a subsequence and relabeling if necessary, it follows that

Again  joins
joins  to
to  and the result follows.
and the result follows.
References
Gupta CP: Existence and uniqueness theorems for the bending of an elastic beam equation. Applicable Analysis 1988, 26(4):289-304. 10.1080/00036818808839715
Gupta CP: Existence and uniqueness results for the bending of an elastic beam equation at resonance. Journal of Mathematical Analysis and Applications 1988, 135(1):208-225. 10.1016/0022-247X(88)90149-7
Ma R: Existence of positive solutions of a fourth-order boundary value problem. Applied Mathematics and Computation 2005, 168(2):1219-1231. 10.1016/j.amc.2004.10.014
Ma R, Xu L: Existence of positive solutions of a nonlinear fourth-order boundary value problem. Applied Mathematics Letters 2010, 23(5):537-543. 10.1016/j.aml.2010.01.007
Li Y: Positive solutions of fourth-order boundary value problems with two parameters. Journal of Mathematical Analysis and Applications 2003, 281(2):477-484. 10.1016/S0022-247X(03)00131-8
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Applicable Analysis 1995, 59(1–4):225-231.
Bai Z, Wang H: On positive solutions of some nonlinear fourth-order beam equations. Journal of Mathematical Analysis and Applications 2002, 270(2):357-368. 10.1016/S0022-247X(02)00071-9
Ma R, Xu J: Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(1):113-122. 10.1016/j.na.2009.06.061
Ma Y: Existence of positive solutions of Lidstone boundary value problems. Journal of Mathematical Analysis and Applications 2006, 314(1):97-108.
Zhang X, Ge W: Positive solutions for a class of boundary-value problems with integral boundary conditions. Computers & Mathematics with Applications 2009, 58(2):203-215. 10.1016/j.camwa.2009.04.002
Gallardo JM: Second-order differential operators with integral boundary conditions and generation of analytic semigroups. The Rocky Mountain Journal of Mathematics 2000, 30(4):1265-1291. 10.1216/rmjm/1021477351
Karakostas GL, Tsamatos PCh: Multiple positive solutions of some integral equations arisen from nonlocal boundary-value problems. Electronic Journal of Differential Equations 2002, 30: 1-17.
Lomtatidze A, Malaguti L: On a nonlocal boundary value problem for second order nonlinear singular differential equations. Georgian Mathematical Journal 2000, 7(1):133-154.
Dancer EN: Global solution branches for positive mappings. Archive for Rational Mechanics and Analysis 1973, 52: 181-192.
Amann H: Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Review 1976, 18(4):620-709. 10.1137/1018114
Zeidler E: Nonlinear Functional Analysis and Its Applications. I. Fixed-point Theorems. Springer, New York, NY, USA; 1986:xxi+897.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Acknowledgments
The authors are very grateful to the anonymous referees for their valuable suggestions. This paper was supported by the NSFC (no. 11061030), the Fundamental Research Funds for the Gansu Universities.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, R., Chen, T. Existence of Positive Solutions of Fourth-Order Problems with Integral Boundary Conditions. Bound Value Probl 2011, 297578 (2011). https://doi.org/10.1155/2011/297578
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/297578
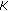 has nonempty interior and
has nonempty interior and  ;
;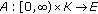 is
is 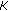 -completely continuous and positive,
-completely continuous and positive, 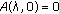 for
for 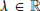 ,
, 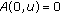 for
for 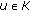 and
and