- Research Article
- Open access
- Published:
Existence of Solutions to Nonlinear Langevin Equation Involving Two Fractional Orders with Boundary Value Conditions
Boundary Value Problems volume 2011, Article number: 516481 (2011)
Abstract
We study a boundary value problem to Langevin equation involving two fractional orders. The Banach fixed point theorem and Krasnoselskii's fixed point theorem are applied to establish the existence results.
1. Introduction
Recently, the subject of fractional differential equations has emerged as an important area of investigation. Indeed, we can find numerous applications in viscoelasticity, electrochemistry, control, electromagnetic, porous media, and so forth. In consequence, the subject of fractional differential equations is gaining much importance and attention. For some recent developments on the subject, see [1–8] and the references therein.
Langevin equation is widely used to describe the evolution of physical phenomena in fluctuating environments. However, for systems in complex media, ordinary Langevin equation does not provide the correct description of the dynamics. One of the possible generalizations of Langevin equation is to replace the ordinary derivative by a fractional derivative in it. This gives rise to fractional Langevin equation, see for instance [9–12] and the references therein.
In this paper, we consider the following boundary value problem of Langevin equation with two different fractional orders:

where  is a positive constant,
is a positive constant,  ,
,  ,
,  , and
, and  are the Caputo fractional derivatives,
are the Caputo fractional derivatives,  is continuous, and
is continuous, and  is a real number.
is a real number.
The organization of this paper is as follows. In Section 2, we recall some definitions of fractional integral and derivative and preliminary results which will be used in this paper. In Section 3, we will consider the existence results for problem (1.1). In Section 4, we will give an example to ensure our main results.
2. Preliminaries
In this section, we present some basic notations, definitions, and preliminary results which will be used throughout this paper.
Definition 2.1.
The Caputo fractional derivative of order  of a function
of a function  , is defined as
, is defined as

where  denotes the integer part of the real number
denotes the integer part of the real number  .
.
Definition 2.2.
The Riemann-Liouville fractional integral of order  of a function
of a function  ,
,  , is defined as
, is defined as

provided that the right side is pointwise defined on  .
.
Definition 2.3.
The Riemann-Liouville fractional derivative of order  of a continuous function
of a continuous function  is given by
is given by

where  and
and  denotes the integer part of real number
denotes the integer part of real number  , provided that the right side is pointwise defined on
, provided that the right side is pointwise defined on  .
.
Lemma 2.4 (see [8]).
Let  , then the fractional differential equation
, then the fractional differential equation  has solution
has solution

where  ,
,  ,
,  .
.
Lemma 2.5 (see [8]).
Let  , then
, then

for some  ,
,  ,
,  .
.
Lemma 2.6.
The unique solution of the following boundary value problem

is given by

Proof.
Similar to the discussion of [9, equation (1.5)], the general solution of

can be written as

By the boundary conditions  and
and  , we obtain
, we obtain

Hence,

Lemma 2.7 (Krasnoselskii s fixed point theorem).
s fixed point theorem).
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  , and let
, and let  ,
,  be the operators such that
be the operators such that
-
(i)
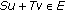 whenever
whenever 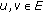 ,
, -
(ii)
 is completely continuous,
is completely continuous, -
(iii)
 is a contraction mapping.
is a contraction mapping.
Then there exists  such that
such that  .
.
Lemma 2.8 (Hölder inequality).
Let  ,
,  ,
,  ,
,  , then the following inequality holds:
, then the following inequality holds:

3. Main Result
In this section, our aim is to discuss the existence and uniqueness of solutions to the problem (1.1).
Let  be a Banach space of all continuous functions from
be a Banach space of all continuous functions from  with the norm
with the norm  .
.
Theorem 3.1.
Assume that
(H1) there exists a real-valued function  for some
for some  such that
such that

If

where  ,
,  ,
,  ,
,  , then problem (1.1) has a unique solution.
, then problem (1.1) has a unique solution.
Proof.
Define an operator  by
by

Let  and choose
and choose

where  is such that
is such that  .
.
Now we show that  , where
, where  . For
. For  , by Hölder inequality, we have
, by Hölder inequality, we have

Take notice of Beta functions:

We can get

Therefore,  .
.
For  and for each
and for each  , based on Hölder inequality, we obtain
, based on Hölder inequality, we obtain

Since  , consequently
, consequently  is a contraction. As a consequence of Banach fixed point theorem, we deduce that
is a contraction. As a consequence of Banach fixed point theorem, we deduce that  has a fixed point which is a solution of problem (1.1).
has a fixed point which is a solution of problem (1.1).
Corollary 3.2.
Assume that
(H1)′ There exists a constant  such that
such that

If

then problem (1.1) has a unique solution.
Theorem 3.3.
Suppose that (H1) and the following condition hold:
(H2) There exists a constant  and a real-valued function
and a real-valued function  such that
such that

Then the problem (1.1) has at least one solution on  if
if

Proof.
Let us fix

here,  ; consider
; consider  , then
, then  is a closed, bounded, and convex subset of Banach space
is a closed, bounded, and convex subset of Banach space  . We define the operators
. We define the operators  and
and  on
on  as
as

For  , based on Hölder inequality, we find that
, based on Hölder inequality, we find that

Thus,  , so
, so  .
.
For  and for each
and for each  , by the analogous argument to the proof of Theorem 3.1, we obtain
, by the analogous argument to the proof of Theorem 3.1, we obtain

From the assumption

it follows that  is a contraction mapping.
is a contraction mapping.
The continuity of  implies that the operator
implies that the operator  is continuous. Also,
is continuous. Also,  is uniformly bounded on
is uniformly bounded on  as
as

On the other hand, let  , for all
, for all  , setting
, setting

For each  , we will prove that if
, we will prove that if  and
and  , then
, then

In fact, we have

In the following, the proof is divided into two cases.
Case 1.
For  , we have
, we have

Case 2.
for  ,
,  , we have.
, we have.

Therefore,  is equicontinuous and the Arzela-Ascoli theorem implies that
is equicontinuous and the Arzela-Ascoli theorem implies that  is compact on
is compact on  , so the operator
, so the operator  is completely continuous.
is completely continuous.
Thus, all the assumptions of Lemma 2.7 are satisfied and the conclusion of Lemma 2.7 implies that the boundary value problem (1.1) has at least one solution on  .
.
Corollary 3.4.
Suppose that the condition (H1)′ hold and, assume that

Further assume that
(H2)′ there exists a constant  such that
such that

then problem (1.1) has at least one solution on  .
.
4. Example
Let  ,
,  ,
,  ,
,  . We consider the following boundary value problem
. We consider the following boundary value problem

where

Because of  , let
, let  , then
, then  , we have
, we have  and
and  . Further,
. Further,

Then BVP (4.1) has a unique solution on  according to Theorem 3.1.
according to Theorem 3.1.
On the other hand, we find that

Then BVP (4.1) has at least one solution on  according to Theorem 3.3.
according to Theorem 3.3.
References
Alsaedi A: Existence of solutions for integrodifferential equations of fractional order with antiperiodic boundary conditions. International Journal of Differential Equations 2009, 2009:-9.
Ahmad B:Existence of solutions for fractional differential equations of order
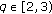 with anti-periodic boundary conditions. Journal of Applied Mathematics and Computing 2010, 34(1-2):385-391. 10.1007/s12190-009-0328-4
with anti-periodic boundary conditions. Journal of Applied Mathematics and Computing 2010, 34(1-2):385-391. 10.1007/s12190-009-0328-4Ahmad B, Otero-Espinar V: Existence of solutions for fractional differential inclusions with antiperiodic boundary conditions. Boundary Value Problems 2009, 2009:-11.
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005, 311(2):495-505. 10.1016/j.jmaa.2005.02.052
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Computers & Mathematics with Applications 2010, 59(3):1363-1375.
Lakshmikantham V, Leela S, Devi JV: Theory of Fractional Dynamic Systems. Cambridge Academic, Cambridge, UK; 2009.
Tian Y, Chen A: The existence of positive solution to three-point singular boundary value problem of fractional differential equation. Abstract and Applied Analysis 2009, 2009:-18.
Zhang S: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electronic Journal of Differential Equations 2006, 2006: 1-12.
Ahmad B, Nieto JJ: Solvability of nonlinear Langevin equation involving two fractional orders with Dirichlet boundary conditions. International Journal of Differential Equations 2010, 2010:-10.
Ahmad B, Eloe P: A nonlocal boundary value problem for a nonlinear fractional differential equation with two indices. Communications on Applied Nonlinear Analysis 2010, 17(3):69-80.
Lim SC, Li M, Teo LP: Langevin equation with two fractional orders. Physics Letters A 2008, 372(42):6309-6320. 10.1016/j.physleta.2008.08.045
Lim SC, Teo LP: The fractional oscillator process with two indices. Journal of Physics A 2009, 42:-34.
Acknowledgments
This work was supported by the Natural Science Foundation of China (10971173), the Natural Science Foundation of Hunan Province (10JJ3096), the Aid Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province, and the Construct Program of the Key Discipline in Hunan Province.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, A., Chen, Y. Existence of Solutions to Nonlinear Langevin Equation Involving Two Fractional Orders with Boundary Value Conditions. Bound Value Probl 2011, 516481 (2011). https://doi.org/10.1155/2011/516481
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/516481
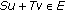 whenever
whenever 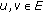 ,
, is completely continuous,
is completely continuous, is a contraction mapping.
is a contraction mapping.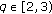 with anti-periodic boundary conditions. Journal of Applied Mathematics and Computing 2010, 34(1-2):385-391. 10.1007/s12190-009-0328-4
with anti-periodic boundary conditions. Journal of Applied Mathematics and Computing 2010, 34(1-2):385-391. 10.1007/s12190-009-0328-4