- Research Article
- Open access
- Published:
Multiple Positive Solutions of Fourth-Order Impulsive Differential Equations with Integral Boundary Conditions and One-Dimensional 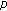 -Laplacian
-Laplacian
Boundary Value Problems volume 2011, Article number: 654871 (2011)
Abstract
By using the fixed point theory for completely continuous operator, this paper investigates the existence of positive solutions for a class of fourth-order impulsive boundary value problems with integral boundary conditions and one-dimensional  -Laplacian. Moreover, we offer some interesting discussion of the associated boundary value problems. Upper and lower bounds for these positive solutions also are given, so our work is new.
-Laplacian. Moreover, we offer some interesting discussion of the associated boundary value problems. Upper and lower bounds for these positive solutions also are given, so our work is new.
1. Introduction
The theory of impulsive differential equations describes processes which experience a sudden change of their state at certain moments. Processes with such a character arise naturally and often, especially in phenomena studied in physics, chemical technology, population dynamics, biotechnology, and economics. For an introduction of the basic theory of impulsive differential equations, see Lakshmikantham et al. [1]; for an overview of existing results and of recent research areas of impulsive differential equations, see Benchohra et al. [2]. The theory of impulsive differential equations has become an important area of investigation in recent years and is much richer than the corresponding theory of differential equations (see, e.g., [3–18] and references cited therein).
Moreover, the theory of boundary-value problems with integral boundary conditions for ordinary differential equations arises in different areas of applied mathematics and physics. For example, heat conduction, chemical engineering, underground water flow, thermo-elasticity, and plasma physics can be reduced to the nonlocal problems with integral boundary conditions. For boundary-value problems with integral boundary conditions and comments on their importance, we refer the reader to the papers by Gallardo [19], Karakostas and Tsamatos [20], Lomtatidze and Malaguti [21], and the references therein. For more information about the general theory of integral equations and their relation with boundary-value problems, we refer to the book of Corduneanu [22] and Agarwal and O'Regan [23].
On the other hand, boundary-value problems with integral boundary conditions constitute a very interesting and important class of problems. They include two, three, multipoint and nonlocal boundary-value problems as special cases. The existence and multiplicity of positive solutions for such problems have received a great deal of attention in the literature. To identify a few, we refer the reader to [24–46] and references therein. In particular, we would like to mention some results of Zhang et al. [34], Kang et al. [44], and Webb et al. [45]. In [34], Zhang et al. studied the following fourth-order boundary value problem with integral boundary conditions

where  is a positive parameter,
is a positive parameter,  ,
,  is the zero element of
is the zero element of  , and
, and  . The authors investigated the multiplicity of positive solutions to problem (1.1) by using the fixed point index theory in cone for strict set contraction operator.
. The authors investigated the multiplicity of positive solutions to problem (1.1) by using the fixed point index theory in cone for strict set contraction operator.
In [44], Kang et al. have improved and generalized the work of [34] by applying the fixed point theory in cone for a strict set contraction operator; they proved that there exist various results on the existence of positive solutions to a class of fourth-order singular boundary value problems with integral boundary conditions

where  and may be singular at
and may be singular at  or
or  ;
;  are continuous and may be singular at
are continuous and may be singular at  , and
, and  ;
;  , and
, and  , and
, and  , and
, and  are nonnegative,
are nonnegative,  .
.
More recently, by using a unified approach, Webb et al. [45] considered the widely studied boundary conditions corresponding to clamped and hinged ends and many nonlocal boundary conditions and established excellent existence results for multiple positive solutions of fourth-order nonlinear equations which model deflections of an elastic beam

subject to various boundary conditions

where  denotes a linear functional on
denotes a linear functional on  given by
given by  involving a Stieltjes integral, and
involving a Stieltjes integral, and  is a function of bounded variation.
is a function of bounded variation.
At the same time, we notice that there has been a considerable attention on  -Laplacian BVPs [18, 32, 35, 36, 38, 42] as
-Laplacian BVPs [18, 32, 35, 36, 38, 42] as  -Laplacian appears in the study of flow through porous media (
-Laplacian appears in the study of flow through porous media ( ), nonlinear elasticity (
), nonlinear elasticity ( ), glaciology (
), glaciology ( ), and so forth. Here, it is worth mentioning that Liu et al. [43] considered the following fourth-order four-point boundary value problem:
), and so forth. Here, it is worth mentioning that Liu et al. [43] considered the following fourth-order four-point boundary value problem:

where  ,
,  , and
, and  . By using upper and lower solution method, fixed-point theorems, and the properties of Green's function
. By using upper and lower solution method, fixed-point theorems, and the properties of Green's function  and
and  , the authors give sufficient conditions for the existence of one positive solution.
, the authors give sufficient conditions for the existence of one positive solution.
Motivated by works mentioned above, in this paper, we consider the existence of positive solutions for a class of boundary value problems with integral boundary conditions of fourth-order impulsive differential equations:

Here  is
is  -Laplace operator, that is,
-Laplace operator, that is,  ,
,  ,
, (where
(where  is fixed positive integer) are fixed points with
is fixed positive integer) are fixed points with  ,
,  where
where  and
and  represent the right-hand limit and left-hand limit of
represent the right-hand limit and left-hand limit of  at
at  , respectively, and
, respectively, and  is nonnegative.
is nonnegative.
For the case of  , problem (1.6) reduces to the problem studied by Zhang et al. in [33]. By using the fixed point theorem in cone, the authors obtained some sufficient conditions for the existence and multiplicity of symmetric positive solutions for a class of
, problem (1.6) reduces to the problem studied by Zhang et al. in [33]. By using the fixed point theorem in cone, the authors obtained some sufficient conditions for the existence and multiplicity of symmetric positive solutions for a class of  -Laplacian fourth-order differential equations with integral boundary conditions.
-Laplacian fourth-order differential equations with integral boundary conditions.
For the case of  , and
, and  , problem (1.6) is related to fourth-order two-points boundary value problem of ODE. Under this case, problem (1.6) has received considerable attention (see, e.g., [40–42] and references cited therein). Aftabizadeh [40] showed the existence of a solution to problem (1.6) under the restriction that
, problem (1.6) is related to fourth-order two-points boundary value problem of ODE. Under this case, problem (1.6) has received considerable attention (see, e.g., [40–42] and references cited therein). Aftabizadeh [40] showed the existence of a solution to problem (1.6) under the restriction that  is a bounded function. Bai and Wang [41] have applied the fixed point theorem and degree theory to establish existence, uniqueness, and multiplicity of positive solutions to problem (1.6). Ma and Wang [42] have proved that there exist at least two positive solutions by applying the existence of positive solutions under the fact that
is a bounded function. Bai and Wang [41] have applied the fixed point theorem and degree theory to establish existence, uniqueness, and multiplicity of positive solutions to problem (1.6). Ma and Wang [42] have proved that there exist at least two positive solutions by applying the existence of positive solutions under the fact that  is either superlinear or sublinear on
is either superlinear or sublinear on  by employing the fixed point theorem of cone extension or compression.
by employing the fixed point theorem of cone extension or compression.
Being directly inspired by [18, 34, 43], in the present paper, we consider some existence results for problem (1.6) in a specially constructed cone by using the fixed point theorem. The main features of this paper are as follows. Firstly, comparing with [39–43], we discuss the impulsive boundary value problem with integral boundary conditions, that is, problem (1.6) includes fourth-order two-, three-, multipoint, and nonlocal boundary value problems as special cases. Secondly, the conditions are weaker than those of [33, 34, 46], and we consider the case  . Finally, comparing with [33, 34, 39–43, 46], upper and lower bounds for these positive solutions also are given. Hence, we improve and generalize the results of [33, 34, 39–43, 46] to some degree, and so, it is interesting and important to study the existence of positive solutions of problem (1.6).
. Finally, comparing with [33, 34, 39–43, 46], upper and lower bounds for these positive solutions also are given. Hence, we improve and generalize the results of [33, 34, 39–43, 46] to some degree, and so, it is interesting and important to study the existence of positive solutions of problem (1.6).
The organization of this paper is as follows. We shall introduce some lemmas in the rest of this section. In Section 2, we provide some necessary background. In particular, we state some properties of the Green's function associated with problem (1.6). In Section 3, the main results will be stated and proved. Finally, in Section 4, we offer some interesting discussion of the associated problem (1.6).
To obtain positive solutions of problem (1.6), the following fixed point theorem in cones is fundamental, which can be found in [47, page 94].
Lemma 1.1.
Let  and
and  be two bounded open sets in Banach space
be two bounded open sets in Banach space  , such that
, such that  and
and  . Let
. Let  be a cone in
be a cone in  and let operator
and let operator  be completely continuous. Suppose that one of the following two conditions is satisfied:
be completely continuous. Suppose that one of the following two conditions is satisfied:
(a) , and
, and  ;
;
(b) , and
, and  .
.
Then,  has at least one fixed point in
has at least one fixed point in  .
.
2. Preliminaries
In order to define the solution of problem (1.6), we shall consider the following space.
Let  , and
, and

Then  is a real Banach space with norm
is a real Banach space with norm

where  .
.
A function  is called a solution of problem (1.6) if it satisfies (1.6).
is called a solution of problem (1.6) if it satisfies (1.6).
To establish the existence of multiple positive solutions in  of problem (1.6), let us list the following assumptions:
of problem (1.6), let us list the following assumptions:
 ;
;
 with
with

Write

From  , it is clear that
, it is clear that  .
.
We shall reduce problem (1.6) to an integral equation. To this goal, firstly by means of the transformation

we convert problem (1.6) into


Lemma 2.1.
Assume that  and
and  hold. Then problem (2.6) has a unique solution
hold. Then problem (2.6) has a unique solution  given by
given by

where


Proof.
The proof follows by routine calculations.
Write  . Then from (2.9) and (2.10), we can prove that
. Then from (2.9) and (2.10), we can prove that  have the following properties.
have the following properties.
Proposition 2.2.
If  holds, then we have
holds, then we have

Proposition 2.3.
For  , we have
, we have

Proposition 2.4.
If  holds, then for
holds, then for  , we have
, we have

where

Proof.
By (2.6) and (2.12), we have

On the other hand, noticing  , we obtain
, we obtain

The proof of Proposition 2.4 is complete.
Remark 2.5.
From (2.9) and (2.13), we can obtain that

Lemma 2.6.
If  and
and  hold, then problem (2.7) has a unique solution
hold, then problem (2.7) has a unique solution  and
and  can be expressed in the following form:
can be expressed in the following form:

where

and  is defined in (2.10).
is defined in (2.10).
Proof.
First suppose that  is a solution of problem (2.7).
is a solution of problem (2.7).
If  it is easy to see by integration of problem (2.7) that
it is easy to see by integration of problem (2.7) that

If  then integrate from
then integrate from  to
to  ,
,

Similarly, if  we have
we have

Integrating again, we can get

Letting  in (2.23), we find
in (2.23), we find

Substituting  and (2.24) into (2.23), we obtain
and (2.24) into (2.23), we obtain

where

Therefore, we have

Let

Then,

and the proof of sufficient is complete.
Conversely, if  is a solution of (2.18).
is a solution of (2.18).
Direct differentiation of (2.18) implies, for  ,
,

Evidently,

The Lemma is proved.
Remark 2.7.
From (2.19), we can prove that the properties of  are similar to that of
are similar to that of  .
.
Suppose that  is a solution of problem (1.6). Then from Lemmas 2.6 and 2.1, we have
is a solution of problem (1.6). Then from Lemmas 2.6 and 2.1, we have

For the sake of applying Lemma 1.1, we construct a cone in  via
via

where

It is easy to see that  is a closed convex cone of
is a closed convex cone of  .
.
Define an operator  by
by

From (2.35), we know that  is a solution of problem (1.6) if and only if
is a solution of problem (1.6) if and only if  is a fixed point of operator
is a fixed point of operator  .
.
Definition 2.8 (see [1]).
The set  is said to be quasi-equicontinuous in
is said to be quasi-equicontinuous in  if for any
if for any  there exist
there exist  such that if
such that if  then
then

We present the following result about relatively compact sets in  which is a consequence of the Arzela-Ascoli Theorem. The reader can find its proof partially in [1].
which is a consequence of the Arzela-Ascoli Theorem. The reader can find its proof partially in [1].
Lemma 2.9.
 is relatively compact if and only if
is relatively compact if and only if  is bounded and quasi-equicontinuous on
is bounded and quasi-equicontinuous on  .
.
Write

where  .
.
Lemma 2.10.
Suppose that  and
and  hold. Then
hold. Then  and
and  is completely continuous.
is completely continuous.
Proof.
For  , it is clear that
, it is clear that  , and
, and

From (2.35) and Remark 2.5, we obtain the following cases.
Case 1.
if  , noticing
, noticing  , then we have
, then we have

Case 2.
if  , noticing
, noticing  and
and  , then we have
, then we have

Therefore,  , that is,
, that is,  . Also, we have
. Also, we have  since
since  . Hence we have
. Hence we have  .
.
Next, we prove that  is completely continuous.
is completely continuous.
It is obvious that  is continuous. Now we prove
is continuous. Now we prove  is relatively compact.
is relatively compact.
Let  be a bounded set. Then, for all
be a bounded set. Then, for all  , we have
, we have

Therefore  is uniformly bounded.
is uniformly bounded.
On the other hand, for all  with
with  , we have
, we have

and by the continuity of  , we have
, we have

and then  is quasi-equicontinuous. It follows that
is quasi-equicontinuous. It follows that  is relatively compact on
is relatively compact on  by Lemma 2.9. So
by Lemma 2.9. So  is completely continuous.
is completely continuous.
3. Main Results
In this section, we apply Lemma 1.1 to establish the existence of positive solutions of problem (1.6). We begin by introducing the following conditions on  and
and  .
.
There exist numbers  such that
such that


where  is defined in (2.4),
is defined in (2.4),  are defined in (2.14), respectively, and write
are defined in (2.14), respectively, and write

where  denotes
denotes  or
or 
Theorem 3.1.
Assume that  hold. Then problem (1.6) has at least one positive solution
hold. Then problem (1.6) has at least one positive solution  with
with

Proof.
Let  be the cone preserving, completely continuous operator that was defined by (2.35). For
be the cone preserving, completely continuous operator that was defined by (2.35). For  with
with  , (2.13), (2.19), and (3.1) imply
, (2.13), (2.19), and (3.1) imply

where

Now if we let  , then (3.5) shows that
, then (3.5) shows that

Further, let

Then,  and
and  implies
implies

that is,

Hence,  for all
for all  . Therefore, for all
. Therefore, for all  , (3.2) implies
, (3.2) implies

that is,  implies
implies

Applying (b) of Lemma 1.1 to (3.7) and (3.12) yields that  has a fixed point
has a fixed point  with
with  . Hence, since for
. Hence, since for  we have
we have  , it follows that (3.4) holds. This and Lemma 2.9 complete the proof.
, it follows that (3.4) holds. This and Lemma 2.9 complete the proof.
As a special case of Theorem 3.1, we can prove the following results.
Corollary 3.2.
Assume that  and
and  hold. If
hold. If  , and
, and  , then, for
, then, for  being sufficiently small and
being sufficiently small and  being sufficiently large, BVP (1.6) has at least one positive solution
being sufficiently large, BVP (1.6) has at least one positive solution  with property (3.4).
with property (3.4).
Proof.
The proof is similar to that of Theorem  of [6].
of [6].
In Theorem 3.3, we assume the following condition on  and
and  .
.
There exist numbers  such that
such that



where  are defined in (2.14), and write
are defined in (2.14), and write

Theorem 3.3.
Assume that  , and
, and  hold. Then problem (1.6) has at least one positive solution
hold. Then problem (1.6) has at least one positive solution  with
with

Proof.
For  with
with  , (3.13) implies
, (3.13) implies

that is,  implies
implies

Next, we turn to (3.14) and (3.15). From (3.14), (3.15), and (3.16), we have

Let

Thus, for  , we have
, we have


Then, (3.22) and (3.23) imply

Applying (a) of Lemma 1.1 to (3.19) and (3.24) yields that  has a fixed point
has a fixed point  with
with  . Hence, since for
. Hence, since for  we have
we have  , it follows that (3.17) holds. This and Lemma 2.9 complete the proof.
, it follows that (3.17) holds. This and Lemma 2.9 complete the proof.
As a special case of Theorem 3.3, we can prove the following results.
Corollary 3.4.
Assume that  and
and  hold. If
hold. If  and
and  ; then, for
; then, for  being sufficiently small and
being sufficiently small and  being sufficiently large, BVP (1.6) has at least one positive solution
being sufficiently large, BVP (1.6) has at least one positive solution  with property (3.17).
with property (3.17).
Proof.
The proof is similar to that of Theorem  of [6].
of [6].
Theorem 3.5.
Assume that  (3.1) of
(3.1) of  and (3.14) and (3.15) of
and (3.14) and (3.15) of  hold. In addition, letting
hold. In addition, letting  and
and  satisfy the following condition:
satisfy the following condition:
There is a  such that
such that  and
and  implies
implies

Then, problem (1.6) has at least two positive solutions  and
and  with
with

where  and
and  satisfy
satisfy

Proof.
If (3.1) of  holds, similar to the proof of (3.7), we can prove that
holds, similar to the proof of (3.7), we can prove that

If (3.14) and (3.15) of  hold, similar to the proof of (3.23), we have
hold, similar to the proof of (3.23), we have

Finally, we show that

In fact, for  with
with  then by (2.18), we have
then by (2.18), we have

and it follows from  that
that

which implies that (3.30) holds.
Applying Lemma 1.1 to (3.28), (3.29), and (3.30) yields that  has two fixed point
has two fixed point  with
with  , and
, and . Hence, since for
. Hence, since for  we have
we have  , it follows that (3.26) holds. This and Lemma 2.9 complete the proof.
, it follows that (3.26) holds. This and Lemma 2.9 complete the proof.
Remark 3.6.
Similar to the proof of that of [5], we can prove that problem (1.6) can be generalized to obtain many positive solutions.
4. Discussion
In this section, we offer some interesting discussions associated with problem (1.6).
Discussion.
Generally, it is difficult to obtain the upper and lower bounds of positive solutions for nonlinear higher-order boundary value problems (see, e.g., [33, 34, 39–43, 46, 48, 49] and their references).
For example, we consider the following problems:

Here  is
is  -Laplace operator, that is,
-Laplace operator, that is,  ,
,  ,
,  (where
(where  is fixed positive integer) are fixed points with
is fixed positive integer) are fixed points with  ,
,  where
where  and
and  represent the right-hand limit and left-hand limit of
represent the right-hand limit and left-hand limit of  at
at  , respectively, and
, respectively, and  is nonnegative.
is nonnegative.
By means of the transformation (2.5), we can convert problem (4.1) into


Using the similar proof of that of Lemmas 2.1 and 2.6, we can obtain the following results. In addition, if we replace  by
by  in
in  , respectively, then we obtain
, respectively, then we obtain  , where
, where

Lemma 4.1.
If  and
and  hold, then BVP (4.2) has a unique solution
hold, then BVP (4.2) has a unique solution  and
and  can be expressed in the form
can be expressed in the form

where

 is defined in (2.10).
is defined in (2.10).
Lemma 4.2.
If  and
and  hold, then BVP (4.3) has a unique solution
hold, then BVP (4.3) has a unique solution  and
and  can be expressed in the form
can be expressed in the form

where

It is not difficult to prove that  and
and  have the similar properties to that of
have the similar properties to that of  and
and  . But for
. But for  ,
,  and
and  have no property (2.13). In fact, if
have no property (2.13). In fact, if  , then we can prove that
, then we can prove that  and
and  have the following properties.
have the following properties.
Proposition 4.3.
If  holds, then for
holds, then for  , we have
, we have


where

Proof.
We only consider (4.9). By (4.3), we have

On the other hand, noticing  , we obtain
, we obtain

Similarly, we can prove that (4.10) holds, too.
Remark 4.4.
Since  ,
,  .
.
From (4.9) and (4.10), we can only define a cone  by
by

which implies that we cannot obtain the lower bounds for the positive solutions of problem (4.1).
5. Example
To illustrate how our main results can be used in practice, we present an example.
Example 5.1.
Consider the following boundary value problem:

where  , and
, and

Conclusion.
Equation(5.1) has at least one positive solution  for
for  with
with

Proof.
By simple computation, we have  . Select
. Select  then for
then for  , we have
, we have

By Theorem 3.1, (5.1) has a positive solution  with
with  .
.
References
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Singapore; 1989:xii+273.
Benchohra M, Henderson J, Ntouyas S: Impulsive Differential Equations and Inclusions, Contemporary Mathematics and Its Applications. Volume 2. Hindawi Publishing Corporation, New York, NY, USA; 2006:xiv+366.
Ahmad B, Sivasundaram S: Existence of solutions for impulsive integral boundary value problems of fractional order. Nonlinear Analysis: Hybrid Systems 2010, 4(1):134-141. 10.1016/j.nahs.2009.09.002
Baĭnov DD, Simeonov PS: Systems with Impulse Effect. Ellis Horwood, Chichester, UK; 1989:255.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations. Volume 14. World Scientific, Singapore; 1995:x+462.
Yan J: Existence of positive periodic solutions of impulsive functional differential equations with two parameters. Journal of Mathematical Analysis and Applications 2007, 327(2):854-868. 10.1016/j.jmaa.2006.04.018
Feng M, Xie D: Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations. Journal of Computational and Applied Mathematics 2009, 223(1):438-448. 10.1016/j.cam.2008.01.024
Nieto JJ: Basic theory for nonresonance impulsive periodic problems of first order. Journal of Mathematical Analysis and Applications 1997, 205(2):423-433. 10.1006/jmaa.1997.5207
Nieto JJ: Impulsive resonance periodic problems of first order. Applied Mathematics Letters 2002, 15(4):489-493. 10.1016/S0893-9659(01)00163-X
Guo D: Multiple positive solutions for first order nonlinear impulsive integro-differential equations in a Banach space. Applied Mathematics and Computation 2003, 143(2-3):233-249. 10.1016/S0096-3003(02)00356-9
Liu X, Guo D: Periodic boundary value problems for a class of second-order impulsive integro-differential equations in Banach spaces. Journal of Mathematical Analysis and Applications 1997, 216(1):284-302. 10.1006/jmaa.1997.5688
Agarwal RP, O'Regan D: Multiple nonnegative solutions for second order impulsive differential equations. Applied Mathematics and Computation 2000, 114(1):51-59. 10.1016/S0096-3003(99)00074-0
Liu B, Yu J:Existence of solution of
 -point boundary value problems of second-order differential systems with impulses. Applied Mathematics and Computation 2002, 125(2-3):155-175. 10.1016/S0096-3003(00)00110-7
-point boundary value problems of second-order differential systems with impulses. Applied Mathematics and Computation 2002, 125(2-3):155-175. 10.1016/S0096-3003(00)00110-7Agarwal RP, Franco D, O'Regan D: Singular boundary value problems for first and second order impulsive differential equations. Aequationes Mathematicae 2005, 69(1-2):83-96. 10.1007/s00010-004-2735-9
Lin X, Jiang D: Multiple positive solutions of Dirichlet boundary value problems for second order impulsive differential equations. Journal of Mathematical Analysis and Applications 2006, 321(2):501-514. 10.1016/j.jmaa.2005.07.076
Jankowski T: Positive solutions of three-point boundary value problems for second order impulsive differential equations with advanced arguments. Applied Mathematics and Computation 2008, 197(1):179-189. 10.1016/j.amc.2007.07.081
Jankowski T: Positive solutions to second order four-point boundary value problems for impulsive differential equations. Applied Mathematics and Computation 2008, 202(2):550-561. 10.1016/j.amc.2008.02.040
Feng M, Du B, Ge W:Impulsive boundary value problems with integral boundary conditions and one-dimensional
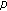 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3119-3126. 10.1016/j.na.2008.04.015
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3119-3126. 10.1016/j.na.2008.04.015Gallardo JM: Second-order differential operators with integral boundary conditions and generation of analytic semigroups. Rocky Mountain Journal of Mathematics 2000, 30(4):1265-1291. 10.1216/rmjm/1021477351
Karakostas GL, Tsamatos PCh: Multiple positive solutions of some Fredholm integral equations arisen from nonlocal boundary-value problems. Electronic Journal of Differential Equations 2002, 2002(30):1-17.
Lomtatidze A, Malaguti L: On a nonlocal boundary value problem for second order nonlinear singular differential equations. Georgian Mathematical Journal 2000, 7(1):133-154.
Corduneanu C: Integral Equations and Applications. Cambridge University Press, Cambridge, UK; 1991:x+366.
Agarwal RP, O'Regan D: Infinite Interval Problems for Differential, Difference and Integral Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+341.
Webb JRL, Infante G: Positive solutions of nonlocal boundary value problems involving integral conditions. Nonlinear Differential Equations and Applications 2008, 15(1-2):45-67. 10.1007/s00030-007-4067-7
Webb JRL, Infante G: Non-local boundary value problems of arbitrary order. Journal of the London Mathematical Society 2009, 79(1):238-258.
Webb JRL, Infante G: Positive solutions of nonlocal boundary value problems: a unified approach. Journal of the London Mathematical Society 2006, 74(3):673-693. 10.1112/S0024610706023179
Ahmad B, Nieto JJ:The monotone iterative technique for three-point second-order integrodifferential boundary value problems with
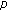 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Ahmad B, Alsaedi A, Alghamdi BS: Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 9(4):1727-1740.
Feng M, Ji D, Ge W: Positive solutions for a class of boundary-value problem with integral boundary conditions in Banach spaces. Journal of Computational and Applied Mathematics 2008, 222(2):351-363. 10.1016/j.cam.2007.11.003
Zhang X, Feng M, Ge W:Multiple positive solutions for a class of
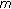 -point boundary value problems. Applied Mathematics Letters 2009, 22(1):12-18. 10.1016/j.aml.2007.10.019
-point boundary value problems. Applied Mathematics Letters 2009, 22(1):12-18. 10.1016/j.aml.2007.10.019Feng M, Ge W:Positive solutions for a class of
 -point singular boundary value problems. Mathematical and Computer Modelling 2007, 46(3-4):375-383. 10.1016/j.mcm.2006.11.009
-point singular boundary value problems. Mathematical and Computer Modelling 2007, 46(3-4):375-383. 10.1016/j.mcm.2006.11.009Zhang X, Feng M, Ge W:Symmetric positive solutions for
 -Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008, 222(2):561-573. 10.1016/j.cam.2007.12.002
-Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008, 222(2):561-573. 10.1016/j.cam.2007.12.002Zhang X, Feng M, Ge W: Existence results for nonlinear boundary-value problems with integral boundary conditions in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(10):3310-3321. 10.1016/j.na.2007.09.020
Yang Z: Positive solutions of a second-order integral boundary value problem. Journal of Mathematical Analysis and Applications 2006, 321(2):751-765. 10.1016/j.jmaa.2005.09.002
Ma R:Positive solutions for multipoint boundary value problem with a one-dimensional
 -Laplacian. Computational & Applied Mathematics 2001, 42: 755-765.
-Laplacian. Computational & Applied Mathematics 2001, 42: 755-765.Bai Z, Huang B, Ge W:The iterative solutions for some fourth-order
 -Laplace equation boundary value problems. Applied Mathematics Letters 2006, 19(1):8-14. 10.1016/j.aml.2004.10.010
-Laplace equation boundary value problems. Applied Mathematics Letters 2006, 19(1):8-14. 10.1016/j.aml.2004.10.010Liu B, Liu L, Wu Y: Positive solutions for singular second order three-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(12):2756-2766. 10.1016/j.na.2006.04.005
Zhang X, Liu L:A necessary and sufficient condition for positive solutions for fourth-order multi-point boundary value problems with
 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3127-3137. 10.1016/j.na.2007.03.006
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3127-3137. 10.1016/j.na.2007.03.006Aftabizadeh AR: Existence and uniqueness theorems for fourth-order boundary value problems. Journal of Mathematical Analysis and Applications 1986, 116(2):415-426. 10.1016/S0022-247X(86)80006-3
Bai Z, Wang H: On positive solutions of some nonlinear fourth-order beam equations. Journal of Mathematical Analysis and Applications 2002, 270(2):357-368. 10.1016/S0022-247X(02)00071-9
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Applicable Analysis 1995, 59(1–4):225-231.
Liu L, Zhang X, Wu Y:Positive solutions of fourth order four-point boundary value problems with
 -Laplacian operator. Journal of Mathematical Analysis and Applications 2007, 326(2):1212-1224. 10.1016/j.jmaa.2006.03.029
-Laplacian operator. Journal of Mathematical Analysis and Applications 2007, 326(2):1212-1224. 10.1016/j.jmaa.2006.03.029Kang P, Wei Z, Xu J: Positive solutions to fourth-order singular boundary value problems with integral boundary conditions in abstract spaces. Applied Mathematics and Computation 2008, 206(1):245-256. 10.1016/j.amc.2008.09.010
Webb JRL, Infante G, Franco D: Positive solutions of nonlinear fourth-order boundary-value problems with local and non-local boundary conditions. Proceedings of the Royal Society of Edinburgh 2008, 138(2):427-446.
Ma H: Symmetric positive solutions for nonlocal boundary value problems of fourth order. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(3):645-651. 10.1016/j.na.2006.11.026
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Eloe PW, Ahmad B:Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009Hao X, Liu L, Wu Y:Positive solutions for nonlinear
 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
Acknowledgments
The authors thank the referee for his/her careful reading of the manuscript and useful suggestions. This work is sponsored by the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHR201008430), the Scientific Research Common Program of Beijing Municipal Commission of Education (KM201010772018), and Beijing Municipal Education Commission (71D0911003).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, M. Multiple Positive Solutions of Fourth-Order Impulsive Differential Equations with Integral Boundary Conditions and One-Dimensional 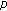 -Laplacian.
Bound Value Probl 2011, 654871 (2011). https://doi.org/10.1155/2011/654871
-Laplacian.
Bound Value Probl 2011, 654871 (2011). https://doi.org/10.1155/2011/654871
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/654871
 -point boundary value problems of second-order differential systems with impulses. Applied Mathematics and Computation 2002, 125(2-3):155-175. 10.1016/S0096-3003(00)00110-7
-point boundary value problems of second-order differential systems with impulses. Applied Mathematics and Computation 2002, 125(2-3):155-175. 10.1016/S0096-3003(00)00110-7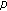 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3119-3126. 10.1016/j.na.2008.04.015
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3119-3126. 10.1016/j.na.2008.04.015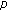 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.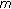 -point boundary value problems. Applied Mathematics Letters 2009, 22(1):12-18. 10.1016/j.aml.2007.10.019
-point boundary value problems. Applied Mathematics Letters 2009, 22(1):12-18. 10.1016/j.aml.2007.10.019 -point singular boundary value problems. Mathematical and Computer Modelling 2007, 46(3-4):375-383. 10.1016/j.mcm.2006.11.009
-point singular boundary value problems. Mathematical and Computer Modelling 2007, 46(3-4):375-383. 10.1016/j.mcm.2006.11.009 -Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008, 222(2):561-573. 10.1016/j.cam.2007.12.002
-Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008, 222(2):561-573. 10.1016/j.cam.2007.12.002 -Laplacian. Computational & Applied Mathematics 2001, 42: 755-765.
-Laplacian. Computational & Applied Mathematics 2001, 42: 755-765. -Laplace equation boundary value problems. Applied Mathematics Letters 2006, 19(1):8-14. 10.1016/j.aml.2004.10.010
-Laplace equation boundary value problems. Applied Mathematics Letters 2006, 19(1):8-14. 10.1016/j.aml.2004.10.010 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3127-3137. 10.1016/j.na.2007.03.006
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3127-3137. 10.1016/j.na.2007.03.006 -Laplacian operator. Journal of Mathematical Analysis and Applications 2007, 326(2):1212-1224. 10.1016/j.jmaa.2006.03.029
-Laplacian operator. Journal of Mathematical Analysis and Applications 2007, 326(2):1212-1224. 10.1016/j.jmaa.2006.03.029 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.