- Research Article
- Open access
- Published:
A Quasilinear Parabolic System with Nonlocal Boundary Condition
Boundary Value Problems volume 2011, Article number: 750769 (2011)
Abstract
We investigate the blow-up properties of the positive solutions to a quasilinear parabolic system with nonlocal boundary condition. We first give the criteria for finite time blowup or global existence, which shows the important influence of nonlocal boundary. And then we establish the precise blow-up rate estimate. These extend the resent results of Wang et al. (2009), which considered the special case  , and Wang et al. (2007), which studied the single equation.
, and Wang et al. (2007), which studied the single equation.
1. Introduction
In this paper, we deal with the following degenerate parabolic system:

with nonlocal boundary condition

and initial data

where  , and
, and  is a bounded connected domain with smooth boundary.
is a bounded connected domain with smooth boundary.  and
and  for the sake of the meaning of nonlocal boundary are nonnegative continuous functions defined for
for the sake of the meaning of nonlocal boundary are nonnegative continuous functions defined for  and
and  , while the initial data
, while the initial data  ,
, are positive continuous functions and satisfy the compatibility conditions
are positive continuous functions and satisfy the compatibility conditions  and
and  for
for  , respectively.
, respectively.
Problem (1.1)–(1.3) models a variety of physical phenomena such as the absorption and "downward infiltration" of a fluid (e.g., water) by the porous medium with an internal localized source or in the study of population dynamics (see [1]). The solution  of the problem (1.1)–(1.3) is said to blow up in finite time if there exists
of the problem (1.1)–(1.3) is said to blow up in finite time if there exists  called the blow-up time such that
called the blow-up time such that

while we say that  exists globally if
exists globally if

Over the past few years, a considerable effort has been devoted to the study of the blow-up properties of solutions to parabolic equations with local boundary conditions, say Dirichlet, Neumann, or Robin boundary condition, which can be used to describe heat propagation on the boundary of container (see the survey papers [2, 3] and references therein). The semilinear case  of (1.1)–(1.3) has been deeply investigated by many authors (see, e.g., [2–11]). The system turns out to be degenerate if
of (1.1)–(1.3) has been deeply investigated by many authors (see, e.g., [2–11]). The system turns out to be degenerate if  ; for example, in [12, 13], Galaktionov et al. studied the following degenerate parabolic equations:
; for example, in [12, 13], Galaktionov et al. studied the following degenerate parabolic equations:

with  ,
,  ,
,  , and
, and  . They obtained that solutions of (1.6) are global if
. They obtained that solutions of (1.6) are global if  , and may blow up in finite time if
, and may blow up in finite time if  . For the critical case of
. For the critical case of  , there should be some additional assumptions on the geometry of
, there should be some additional assumptions on the geometry of  .
.
Song et al. [14] considered the following nonlinear diffusion system with  coupled via more general sources:
coupled via more general sources:

Recently, the genuine degenerate situation with zero boundary values for (1.7) has been discussed by Lei and Zheng [15]. Clearly, problem (1.6) is just the special case by taking  in (1.7) with zero boundary condition.
in (1.7) with zero boundary condition.
For the more parabolic problems related to the local boundary, we refer to the recent works [16–20] and references therein.
On the other hand, there are a number of important phenomena modeled by parabolic equations coupled with nonlocal boundary condition of form (1.2). In this case, the solution could be used to describe the entropy per volume of the material (see [21–23]). Over the past decades, some basic results such as the global existence and decay property have been obtained for the nonlocal boundary problem (1.1)–(1.3) in the case of scalar equation (see [24–28]). In particular, in [28], Wang et al. studied the following problem:

with  . They obtained the blow-up condition and its blow-up rate estimate. For the special case
. They obtained the blow-up condition and its blow-up rate estimate. For the special case  in the system (1.8), under the assumption that
in the system (1.8), under the assumption that  , Seo [26] established the following blow-up rate estimate:
, Seo [26] established the following blow-up rate estimate:

for any  For the more nonlocal boundary problems, we also mention the recent works [29–34]. In particular, Kong and Wang in [29], by using some ideas of Souplet [35], obtained the blow-up conditions and blow-up profile of the following system:
For the more nonlocal boundary problems, we also mention the recent works [29–34]. In particular, Kong and Wang in [29], by using some ideas of Souplet [35], obtained the blow-up conditions and blow-up profile of the following system:

subject to nonlocal boundary (1.2), and Zheng and Kong in [34] gave the condition for global existence or nonexistence of solutions to the following similar system:

with nonlocal boundary condition (1.2). The typical characterization of systems (1.10) and (1.11) is the complete couple of the nonlocal sources, which leads to the analysis of simultaneous blowup.
Recently, Wang and Xiang [30] studied the following semilinear parabolic system with nonlocal boundary condition:

where  and
and  are positive parameters. They gave the criteria for finite time blowup or global existence, and established blow-up rate estimate.
are positive parameters. They gave the criteria for finite time blowup or global existence, and established blow-up rate estimate.
To our knowledge, there is no work dealing with the parabolic system (1.1) with nonlocal boundary condition (1.2) except for the single equation case, although this is a very classical model. Therefore, the main purpose of this paper is to understand how the reaction terms, the weight functions and the nonlinear diffusion affect the blow-up properties for the problem (1.1)–(1.3). We will show that the weight functions  play substantial roles in determining blowup or not of solutions. Firstly, we establish the global existence and finite time blow-up of the solution. Secondly, we establish the precise blowup rate estimates for all solutions which blow up.
play substantial roles in determining blowup or not of solutions. Firstly, we establish the global existence and finite time blow-up of the solution. Secondly, we establish the precise blowup rate estimates for all solutions which blow up.
Our main results could be stated as follows.
Theorem 1.1.
Suppose that  for any
for any  . If
. If  and
and  hold, then any solution to (1.1)–(1.3) with positive initial data blows up in finite time.
hold, then any solution to (1.1)–(1.3) with positive initial data blows up in finite time.
Theorem 1.2 ..
Suppose that  for any
for any  .
.
(1)If  , and
, and  , then every nonnegative solution of (1.1)–(1.3) is global.
, then every nonnegative solution of (1.1)–(1.3) is global.
(2)If  ,
,  or
or  , then the nonnegative solution of (1.1)–(1.3) exists globally for sufficiently small initial values and blows up in finite time for sufficiently large initial values.
, then the nonnegative solution of (1.1)–(1.3) exists globally for sufficiently small initial values and blows up in finite time for sufficiently large initial values.
To establish blow-up rate of the blow-up solution, we need the following assumptions on the initial data 
(1) for some
for some  ;
;
(2) There exists a constant  , such tha
, such tha

where  ,
,  , and
, and  will be given in Section 4.
will be given in Section 4.
Theorem 1.3 ..
Suppose that  for any
for any  ;
;  and satisfy
and satisfy  and
and  ; assumptions (H1)-(H2) hold. If the solution
; assumptions (H1)-(H2) hold. If the solution  of (1.1)–(1.3) with positive initial data
of (1.1)–(1.3) with positive initial data  blows up in finite time
blows up in finite time  , then there exist constants
, then there exist constants  such that
such that

This paper is organized as follows. In the next section, we give the comparison principle of the solution of problem (1.1)–(1.3) and some important lemmas. In Section 3, we concern the global existence and nonexistence of solution of problem (1.1)–(1.3) and show the proofs of Theorems 1.1 and 1.2. In Section 4, we will give the estimate of the blow-up rate.
2. Preliminaries
In this section, we give some basic preliminaries. For convenience, we denote that  for
for  . As it is now well known that degenerate equations need not posses classical solutions, we begin by giving a precise definition of a weak solution for problem (1.1)–(1.3).
. As it is now well known that degenerate equations need not posses classical solutions, we begin by giving a precise definition of a weak solution for problem (1.1)–(1.3).
Definition 2.1 ..
A vector function
 defined on
defined on
 , for some
, for some
 , is called a sub (or super) solution of ( 1.1 )–( 1.3 ), if all the following hold:
, is called a sub (or super) solution of ( 1.1 )–( 1.3 ), if all the following hold:
(1) ;
;
(2) for
for  , and
, and  for almost all
for almost all  ;
;
-
(3)
 (2.1)
(2.1)
where  is the unit outward normal to the lateral boundary of
is the unit outward normal to the lateral boundary of  . For every
. For every  and any ϕ belong to the class of test functions,
and any ϕ belong to the class of test functions,

A weak solution of (1.1) is a vector function which is both a subsolution and a supersolution of (1.1)-(1.3).
Lemma 2.2 (Comparison principle).
Let and
and  be a subsolution and supersolution of (1.1)–(1.3) in
be a subsolution and supersolution of (1.1)–(1.3) in  , respectively. Then
, respectively. Then  in
in  , if
, if 
Proof.
Let  , the subsolution
, the subsolution  satisfies
satisfies

On the other hand, the supersolution  satisfies the reversed inequality
satisfies the reversed inequality

Set  , we have
, we have

where

Since  and
and  are bounded in
are bounded in  , it follows from
, it follows from  ,
,  ,
,  that
that  are bounded nonnegative functions.
are bounded nonnegative functions.  is a function between
is a function between  and
and  . Noticing that
. Noticing that  and
and  are nonnegative bounded function and
are nonnegative bounded function and  on
on  , we choose appropriate function
, we choose appropriate function  as in [36] to obtain that
as in [36] to obtain that

By Gronwall's inequality, we know that  ,
,  can be obtained in similar way, then
can be obtained in similar way, then  .
.
Local in time existence of positive classical solutions of the problem (1.1)–(1.3) can be obtained using fixed point theorem (see [37]), the representation formula and the contraction mapping principle as in [38]. By the above comparison principle, we get the uniqueness of the solution to the problem. The proof is more or less standard, so is omitted here.
Remark 2.3.
From Lemma 2.2, it is easy to see that the solution of (1.1)–(1.3) is unique if  .
.
The following comparison lemma plays a crucial role in our proof which can be obtained by similar arguments as in [24, 38–40]
Lemma 2.4.
Suppose that  and satisfy
and satisfy

where  are bounded functions and
are bounded functions and  , and
, and  and is not identically zero. Then
and is not identically zero. Then  for
for  imply that
imply that  in
in  . Moreover, if
. Moreover, if  or if
or if  , then
, then  for
for  imply that
imply that  in
in 
Denote that

We give some lemmas that will be used in the following section. Please see [41] for their proofs.
Lemma 2.5.
If  , and
, and  , then there exist two positive constants
, then there exist two positive constants  , such that
, such that  . Moreover,
. Moreover,  for any
for any  .
.
Lemma 2.6 ..
If  ,
,  or
or  , then there exist two positive constants
, then there exist two positive constants  , such that
, such that  . Moreover,
. Moreover,  for any
for any  .
.
3. Global Existence and Blowup in Finite Time
Compared with usual homogeneous Dirichlet boundary data, the weight functions  and
and  play an important role in the global existence or global nonexistence results for problem (1.1)–(1.3).
play an important role in the global existence or global nonexistence results for problem (1.1)–(1.3).
Proof of Theorem 1.1..
We consider the ODE system

where  , and we use the assumption
, and we use the assumption 
Set

with

It is easy to check that  is the unique solution of the ODE problem (3.1), then
is the unique solution of the ODE problem (3.1), then  and
and  imply that
imply that  blows up in finite time. Under the assumption that
blows up in finite time. Under the assumption that  for any
for any  ,
,  is a subsolution of problem (1.1)–(1.3). Therefore, by Lemma 2.2, we see that the solution
is a subsolution of problem (1.1)–(1.3). Therefore, by Lemma 2.2, we see that the solution  of problem (1.1)–(1.3) satisfies
of problem (1.1)–(1.3) satisfies  and then
and then  blows up in finite time.
blows up in finite time.
Proof of Theorem 1.2.
-
(1)
Let
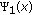 be the positive solution of the linear elliptic problem
be the positive solution of the linear elliptic problem  (3.4)
(3.4)
and  be the positive solution of the linear elliptic problem
be the positive solution of the linear elliptic problem

where  are positive constant such that
are positive constant such that  . We remark that
. We remark that  and
and  ensure the existence of such
ensure the existence of such  .
.
Denote that

We define the functions  as following:
as following:

where  is a constant to be determined later. Then, we have
is a constant to be determined later. Then, we have

In a similar way, we can obtain that

here, we used 
 , and
, and  .
.
On the other hand, we have


Let

If  , and
, and  , by Lemma 2.5, there exist positive constants
, by Lemma 2.5, there exist positive constants  such that
such that

Therefore, we can choose  sufficiently large, such that
sufficiently large, such that


Now, it follows from (3.8)–(3.15) that  defined by (3.7) is a positive supersolution of (1.1)–(1.3).
defined by (3.7) is a positive supersolution of (1.1)–(1.3).
By comparison principle, we conclude that  , which implies
, which implies  exists globally.
exists globally.
-
(2)
If
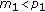 ,
, 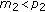 or
or  , by Lemma 2.6, there exist positive constants
, by Lemma 2.6, there exist positive constants 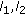 such that
such that  (3.16)
(3.16)
So we can choose  . Furthermore, assume that
. Furthermore, assume that  are small enough to satisfy (3.15). It follows that
are small enough to satisfy (3.15). It follows that  defined by (3.7) is a positive supersolution of (1.1)–(1.3). Hence,
defined by (3.7) is a positive supersolution of (1.1)–(1.3). Hence,  exists globally.
exists globally.
Due to the requirement of the comparison principle we will construct blow-up subsolutions in some subdomain of  in which
in which  . We use an idea from Souplet [42] and apply it to degenerate equations. Let
. We use an idea from Souplet [42] and apply it to degenerate equations. Let  be a nontrivial nonnegative continuous function and vanished on
be a nontrivial nonnegative continuous function and vanished on  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  and
and  . We will construct a blow-up positive subsolution to complete the proof.
. We will construct a blow-up positive subsolution to complete the proof.
Set

with

where  and
and  are to be determined later. Clearly,
are to be determined later. Clearly,  and
and  is nonincreasing since
is nonincreasing since  Note that
Note that

for sufficiently small  . Obviously,
. Obviously,  becomes unbounded as
becomes unbounded as  , at the point
, at the point  . Calculating directly, we obtain that
. Calculating directly, we obtain that


notice that  is sufficiently small.
is sufficiently small.
Similarly, we have

Case 1.
If  , we have
, we have  , then
, then

Hence,

Case 2.
If  , then
, then

By Lemma 2.6, there exist positive constants  large enough to satisfy
large enough to satisfy

and we can choose  be sufficiently small that
be sufficiently small that

Thus, we have

Hence, for sufficiently small  , (3.24) and (3.25) imply that
, (3.24) and (3.25) imply that


Since  and
and  is continuous, there exist two positive constants
is continuous, there exist two positive constants  and
and  such that
such that  , for all
, for all  . Choose
. Choose  small enough to insure
small enough to insure  , hence
, hence  on
on  . Under the assumption that
. Under the assumption that  and
and  for any
for any  , we have
, we have  and
and  Furthermore, choose
Furthermore, choose  so large that
so large that  . By comparison principle, we have
. By comparison principle, we have  . It shows that solution
. It shows that solution  to (1.1)–(1.3) blows up in finite time.
to (1.1)–(1.3) blows up in finite time.
4. Blow-Up Rate Estimates
In this section, we will estimate the blow-up rate of the blow-up solution of (1.1). Throughout this section, we will assume that

To obtain the estimate, we firstly introduce some transformations. Let 
 then problem (1.1)–(1.3) becomes
then problem (1.1)–(1.3) becomes

where  ,
,  ;
;  ,
,  ;
;  ,
,  ,
,  ,
,  ;
;  ,
,  ;
;  ,
,  . By the conditions (4.1), we have
. By the conditions (4.1), we have  and satisfy that
and satisfy that  . Under this transformation, assumptions
. Under this transformation, assumptions  -
- become
become
() , for some
, for some  ;
;
() there exists a constant  , such that
, such that

where  will be given later.
will be given later.
By the standard method [16, 42], we can show that system (4.2) has a smooth nonnegative solution  , provided that
, provided that  satisfy the hypotheses
satisfy the hypotheses  -
- . We thus assume that the solution
. We thus assume that the solution  of problem (4.2) blows up in the finite time
of problem (4.2) blows up in the finite time  . Denote
. Denote  . We can obtain the blow-up rate from the following lemmas.
. We can obtain the blow-up rate from the following lemmas.
Lemma 4.1.
Suppose that  satisfy
satisfy  -
- , then there exists a positive constant
, then there exists a positive constant  such that
such that

Proof.
By (4.2), we have (see [43])

Noticing that  and
and  , hence we have
, hence we have

by virtue of Young's inequality. Integrating (4.6) from  to
to  , we can obtain (4.4).
, we can obtain (4.4).
Lemma 4.2.
Suppose that  satisfy
satisfy  -
- ,
,  is a solution of (4.2). Then
is a solution of (4.2). Then

where

Proof.
Set  a straightforward computation yields
a straightforward computation yields

If  , obviously we have
, obviously we have

Otherwise, noticing that  , by virtue of Young's inequality,
, by virtue of Young's inequality,

where  we have
we have

Similarly, we also have

Fix  , we have
, we have

where  . Since
. Since  , we have
, we have

Noticing that  by virtue of Jensen's inequality, we have
by virtue of Jensen's inequality, we have

here, we used  and
and  in the last inequality. Hence
in the last inequality. Hence 

Similarly, we also have

On the other hand,  -
- imply that
imply that  Combined inequalities (4.12)-(4.18) and Lemma 2.4, we obtain
Combined inequalities (4.12)-(4.18) and Lemma 2.4, we obtain  that is, (4.7) holds.Integrating (4.7) from
that is, (4.7) holds.Integrating (4.7) from  to
to  , we conclude that
, we conclude that

where  are positive constants independent of
are positive constants independent of  . It follows from Lemma 4.1 and (4.19), we have the following lemma.
. It follows from Lemma 4.1 and (4.19), we have the following lemma.
Lemma 4.3.
Suppose that  satisfy
satisfy  -
- . If
. If  is the solution of system (4.2) and blows up in finite time
is the solution of system (4.2) and blows up in finite time  , then there exist positive constants
, then there exist positive constants  such that
such that

According the transform and Lemma 4.3, we can obtain Theorem 1.3.
References
Diaz JI, Kersner R: On a nonlinear degenerate parabolic equation in infiltration or evaporation through a porous medium. Journal of Differential Equations 1987, 69(3):368-403. 10.1016/0022-0396(87)90125-2
Deng K, Levine HA: The role of critical exponents in blow-up theorems: the sequel. Journal of Mathematical Analysis and Applications 2000, 243(1):85-126. 10.1006/jmaa.1999.6663
Levine HA: The role of critical exponents in blowup theorems. SIAM Review 1990, 32(2):262-288. 10.1137/1032046
Chen H: Global existence and blow-up for a nonlinear reaction-diffusion system. Journal of Mathematical Analysis and Applications 1997, 212(2):481-492. 10.1006/jmaa.1997.5522
Escobedo M, Herrero MA: Boundedness and blow up for a semilinear reaction-diffusion system. Journal of Differential Equations 1991, 89(1):176-202. 10.1016/0022-0396(91)90118-S
Escobedo M, Levine HA: Critical blowup and global existence numbers for a weakly coupled system of reaction-diffusion equations. Archive for Rational Mechanics and Analysis 1995, 129(1):47-100. 10.1007/BF00375126
Levine HA: A Fujita type global existence–global nonexistence theorem for a weakly coupled system of reaction-diffusion equations. Zeitschrift für Angewandte Mathematik und Physik 1991, 42(3):408-430. 10.1007/BF00945712
Quirós F, Rossi JD: Non-simultaneous blow-up in a semilinear parabolic system. Zeitschrift für Angewandte Mathematik und Physik 2001, 52(2):342-346. 10.1007/PL00001549
Wang M: Global existence and finite time blow up for a reaction-diffusion system. Zeitschrift für Angewandte Mathematik und Physik 2000, 51(1):160-167. 10.1007/PL00001504
Zheng S: Global boundedness of solutions to a reaction-diffusion system. Mathematical Methods in the Applied Sciences 1999, 22(1):43-54. 10.1002/(SICI)1099-1476(19990110)22:1<43::AID-MMA19>3.0.CO;2-8
Zheng S: Global existence and global non-existence of solutions to a reaction-diffusion system. Nonlinear Analysis: Theory, Methods & Applications 2000, 39(3):327-340. 10.1016/S0362-546X(98)00171-0
Galaktionov VA, Kurdyumov SP, Samarskiĭ AA: A parabolic system of quasilinear equations. I. Differentsial'nye Uravneniya 1983, 19(12):2123-2140.
Galaktionov VA, Kurdyumov SP, Samarskiĭ AA: A parabolic system of quasilinear equations. II. Differentsial'nye Uravneniya 1985, 21(9):1049-1062.
Song X, Zheng S, Jiang Z: Blow-up analysis for a nonlinear diffusion system. Zeitschrift für Angewandte Mathematik und Physik 2005, 56(1):1-10. 10.1007/s00033-004-1152-1
Lei P, Zheng S: Global and nonglobal weak solutions to a degenerate parabolic system. Journal of Mathematical Analysis and Applications 2006, 324(1):177-198. 10.1016/j.jmaa.2005.12.012
Duan Z, Deng W, Xie C: Uniform blow-up profile for a degenerate parabolic system with nonlocal source. Computers & Mathematics with Applications 2004, 47(6-7):977-995. 10.1016/S0898-1221(04)90081-8
Li Z, Mu C, Cui Z: Critical curves for a fast diffusive polytropic filtration system coupled via nonlinear boundary flux. Zeitschrift fur Angewandte Mathematik und Physik 2009, 60(2):284-296. 10.1007/s00033-008-7095-1
Li Z, Cui Z, Mu C: Critical curves for fast diffusive polytropic filtration equations coupled through boundary. Applicable Analysis 2008, 87(9):1041-1052. 10.1080/00036810802428912
Zhou J, Mu C: On the critical Fujita exponent for a degenerate parabolic system coupled via nonlinear boundary flux. Proceedings of the Edinburgh Mathematical Society. Series II 2008, 51(3):785-805. 10.1017/S0013091505001537
Zhou J, Mu C: The critical curve for a non-Newtonian polytropic filtration system coupled via nonlinear boundary flux. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(1):1-11. 10.1016/j.na.2006.10.022
Day WA: A decreasing property of solutions of parabolic equations with applications to thermoelasticity. Quarterly of Applied Mathematics 1983, 40(4):468-475.
Day WA: Heat Conduction within Linear Thermoelasticity, Springer Tracts in Natural Philosophy. Volume 30. Springer, New York, NY, USA; 1985:viii+83.
Friedman A: Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions. Quarterly of Applied Mathematics 1986, 44(3):401-407.
Deng K: Comparison principle for some nonlocal problems. Quarterly of Applied Mathematics 1992, 50(3):517-522.
Pao CV: Asymptotic behavior of solutions of reaction-diffusion equations with nonlocal boundary conditions. Journal of Computational and Applied Mathematics 1998, 88(1):225-238. 10.1016/S0377-0427(97)00215-X
Seo S: Blowup of solutions to heat equations with nonlocal boundary conditions. Kobe Journal of Mathematics 1996, 13(2):123-132.
Seo S: Global existence and decreasing property of boundary values of solutions to parabolic equations with nonlocal boundary conditions. Pacific Journal of Mathematics 2000, 193(1):219-226. 10.2140/pjm.2000.193.219
Wang Y, Mu C, Xiang Z: Blowup of solutions to a porous medium equation with nonlocal boundary condition. Applied Mathematics and Computation 2007, 192(2):579-585. 10.1016/j.amc.2007.03.036
Kong L, Wang M: Global existence and blow-up of solutions to a parabolic system with nonlocal sources and boundaries. Science in China. Series A 2007, 50(9):1251-1266. 10.1007/s11425-007-0105-5
Wang Y, Xiang Z: Blowup analysis for a semilinear parabolic system with nonlocal boundary condition. Boundary Value Problems 2009, 2009:-14.
Wang Y, Mu C, Xiang Z: Properties of positive solution for nonlocal reaction-diffusion equation with nonlocal boundary. Boundary Value Problems 2007, 2007:-12.
Yin H-M: On a class of parabolic equations with nonlocal boundary conditions. Journal of Mathematical Analysis and Applications 2004, 294(2):712-728. 10.1016/j.jmaa.2004.03.021
Yin Y: On nonlinear parabolic equations with nonlocal boundary condition. Journal of Mathematical Analysis and Applications 1994, 185(1):161-174. 10.1006/jmaa.1994.1239
Zheng S, Kong L: Roles of weight functions in a nonlinear nonlocal parabolic system. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(8):2406-2416. 10.1016/j.na.2007.01.067
Souplet P: Uniform blow-up profiles and boundary behavior for diffusion equations with nonlocal nonlinear source. Journal of Differential Equations 1999, 153(2):374-406. 10.1006/jdeq.1998.3535
Anderson JR: Local existence and uniqueness of solutions of degenerate parabolic equations. Communications in Partial Differential Equations 1991, 16(1):105-143. 10.1080/03605309108820753
Day WA: Extensions of a property of the heat equation to linear thermoelasticity and other theories. Quarterly of Applied Mathematics 1982, 40(3):319-330.
Lin Z, Liu Y: Uniform blowup profiles for diffusion equations with nonlocal source and nonlocal boundary. Acta Mathematica Scientia. Series B 2004, 24(3):443-450.
Pao CV: Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York, NY, USA; 1992:xvi+777.
Pao CV: Blowing-up of solution for a nonlocal reaction-diffusion problem in combustion theory. Journal of Mathematical Analysis and Applications 1992, 166(2):591-600. 10.1016/0022-247X(92)90318-8
Deng W: Global existence and finite time blow up for a degenerate reaction-diffusion system. Nonlinear Analysis: Theory, Methods & Applications 2005, 60(5):977-991. 10.1016/j.na.2004.10.016
Souplet P: Blow-up in nonlocal reaction-diffusion equations. SIAM Journal on Mathematical Analysis 1998, 29(6):1301-1334. 10.1137/S0036141097318900
Friedman A, McLeod B: Blow-up of positive solutions of semilinear heat equations. Indiana University Mathematics Journal 1985, 34(2):425-447. 10.1512/iumj.1985.34.34025
Acknowledgments
The authors would like to thank the anonymous referees for their suggestions and comments on the original manuscript. This work was partially supported by NSF of China (10771226) and partially supported by the Educational Science Foundation of Chongqing (KJ101303), China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, B., Mi, Y. & Mu, C. A Quasilinear Parabolic System with Nonlocal Boundary Condition. Bound Value Probl 2011, 750769 (2011). https://doi.org/10.1155/2011/750769
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/750769

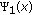 be the positive solution of the linear elliptic problem
be the positive solution of the linear elliptic problem 
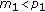 ,
, 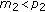 or
or  , by Lemma 2.6, there exist positive constants
, by Lemma 2.6, there exist positive constants 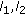 such that
such that 