- Research Article
- Open access
- Published:
Positive Solutions for Integral Boundary Value Problem with ϕ-Laplacian Operator
Boundary Value Problems volume 2011, Article number: 827510 (2011)
Abstract
We consider the existence, multiplicity of positive solutions for the integral boundary value problem with  -Laplacian
-Laplacian  ,
,  ,
,  ,
,  , where
, where  is an odd, increasing homeomorphism from
is an odd, increasing homeomorphism from  onto
onto  . We show that it has at least one, two, or three positive solutions under some assumptions by applying fixed point theorems. The interesting point is that the nonlinear term
. We show that it has at least one, two, or three positive solutions under some assumptions by applying fixed point theorems. The interesting point is that the nonlinear term  is involved with the first-order derivative explicitly.
is involved with the first-order derivative explicitly.
1. Introduction
We are interested in the existence of positive solutions for the integral boundary value problem

where  , and
, and  satisfy the following conditions.
satisfy the following conditions.
(H1) is an odd, increasing homeomorphism from
is an odd, increasing homeomorphism from  onto
onto  , and there exist two increasing homeomorphisms
, and there exist two increasing homeomorphisms  and
and  of
of  onto
onto  such that
such that

Moreover,  , where
, where  denotes the inverse of
denotes the inverse of  .
.
(H2) is continuous.
is continuous.  are nonnegative, and
are nonnegative, and  ,
,  .
.
The assumption (H1) on the function  was first introduced by Wang [1, 2], it covers two important cases:
was first introduced by Wang [1, 2], it covers two important cases:  and
and  . The existence of positive solutions for two above cases received wide attention (see [3–10]). For example, Ji and Ge [4] studied the multiplicity of positive solutions for the multipoint boundary value problem
. The existence of positive solutions for two above cases received wide attention (see [3–10]). For example, Ji and Ge [4] studied the multiplicity of positive solutions for the multipoint boundary value problem

where  ,
,  . They provided sufficient conditions for the existence of at least three positive solutions by using Avery-Peterson fixed point theorem. In [5], Feng et al. researched the boundary value problem
. They provided sufficient conditions for the existence of at least three positive solutions by using Avery-Peterson fixed point theorem. In [5], Feng et al. researched the boundary value problem

where the nonlinear term  does not depend on the first-order derivative and
does not depend on the first-order derivative and  ,
,  . They obtained at least one or two positive solutions under some assumptions imposed on the nonlinearity of
. They obtained at least one or two positive solutions under some assumptions imposed on the nonlinearity of  by applying Krasnoselskii fixed point theorem.
by applying Krasnoselskii fixed point theorem.
As for integral boundary value problem, when  is linear, the existence of positive solutions has been obtained (see [8–10]). In [8], the author investigated the positive solutions for the integral boundary value problem
is linear, the existence of positive solutions has been obtained (see [8–10]). In [8], the author investigated the positive solutions for the integral boundary value problem

The main tools are the priori estimate method and the Leray-Schauder fixed point theorem. However, there are few papers dealing with the existence of positive solutions when  satisfies (H1) and
satisfies (H1) and  depends on both
depends on both  and
and  . This paper fills this gap in the literature. The aim of this paper is to establish some simple criteria for the existence of positive solutions of BVP(1.1). To get rid of the difficulty of
. This paper fills this gap in the literature. The aim of this paper is to establish some simple criteria for the existence of positive solutions of BVP(1.1). To get rid of the difficulty of  depending on
depending on  , we will define a special norm in Banach space (in Section 2).
, we will define a special norm in Banach space (in Section 2).
This paper is organized as follows. In Section 2, we present some lemmas that are used to prove our main results. In Section 3, the existence of one or two positive solutions for BVP(1.1) is established by applying the Krasnoselskii fixed point theorem. In Section 4, we give the existence of three positive solutions for BVP(1.1) by using a new fixed point theorem introduced by Avery and Peterson. In Section 5, we give some examples to illustrate our main results.
2. Preliminaries
The basic space used in this paper is a real Banach space  with norm
with norm  defined by
defined by  , where
, where  . Let
. Let

It is obvious that  is a cone in
is a cone in  .
.
Lemma 2.1 (see [7]).
Let  , then
, then  ,
,  .
.
Lemma 2.2.
Let  , then there exists a constant
, then there exists a constant  such that
such that  .
.
Proof.
The mean value theorem guarantees that there exists  , such that
, such that

Moreover, the mean value theorem of differential guarantees that there exists  , such that
, such that

So we have

Denote  ; then the proof is complete.
; then the proof is complete.
Lemma 2.3.
Assume that (H1), (H2) hold. If  is a solution of BVP(1.1), there exists a unique
is a solution of BVP(1.1), there exists a unique  , such that
, such that  and
and  ,
,  .
.
Proof.
From the fact that  , we know that
, we know that  is strictly decreasing. It follows that
is strictly decreasing. It follows that  is also strictly decreasing. Thus,
is also strictly decreasing. Thus,  is strictly concave on [0, 1]. Without loss of generality, we assume that
is strictly concave on [0, 1]. Without loss of generality, we assume that  . By the concavity of
. By the concavity of  , we know that
, we know that  ,
,  . So we get
. So we get  . By
. By  , it is obvious that
, it is obvious that  . Hence,
. Hence,  ,
,  .
.
On the other hand, from the concavity of  , we know that there exists a unique
, we know that there exists a unique  where the maximum is attained. By the boundary conditions and
where the maximum is attained. By the boundary conditions and  , we know that
, we know that  or 1, that is,
or 1, that is,  such that
such that  and then
and then  .
.
Lemma 2.4.
Assume that (H1), (H2) hold. Suppose  is a solution of BVP(1.1); then
is a solution of BVP(1.1); then

or

Proof.
First, by integrating (1.1) on  , we have
, we have

then

Thus

or

According to the boundary condition, we have

By a similar argument in [5],  ; then the proof is completed.
; then the proof is completed.
Now we define an operator  by
by

Lemma 2.5.
 is completely continuous.
is completely continuous.
Proof.
Let  ; then from the definition of
; then from the definition of  , we have
, we have

So  is monotone decreasing continuous and
is monotone decreasing continuous and  . Hence,
. Hence,  is nonnegative and concave on [0, 1]. By computation, we can get
is nonnegative and concave on [0, 1]. By computation, we can get  . This shows that
. This shows that  . The continuity of
. The continuity of  is obvious since
is obvious since  is continuous. Next, we prove that
is continuous. Next, we prove that  is compact on
is compact on  .
.
Let  be a bounded subset of
be a bounded subset of  and
and  is a constant such that
is a constant such that  for
for  . From the definition of
. From the definition of  , for any
, for any  , we get
, we get

Hence,  is uniformly bounded and equicontinuous. So we have that
is uniformly bounded and equicontinuous. So we have that  is compact on
is compact on  . From (2.13), we know for
. From (2.13), we know for  ,
,  , such that when
, such that when  , we have
, we have  . So
. So  is compact on
is compact on  ; it follows that
; it follows that  is compact on
is compact on  . Therefore,
. Therefore,  is compact on
is compact on  .
.
Thus,  is completely continuous.
is completely continuous.
It is easy to prove that each fixed point of  is a solution for BVP(1.1).
is a solution for BVP(1.1).
Lemma 2.6 (see [1]).
Assume that (H1) holds. Then for  ,
,

To obtain positive solution for BVP(1.1), the following definitions and fixed point theorems in a cone are very useful.
Definition 2.7.
The map  is said to be a nonnegative continuous concave functional on a cone of a real Banach space
is said to be a nonnegative continuous concave functional on a cone of a real Banach space  provided that
provided that  is continuous and
is continuous and

for all  and
and  . Similarly, we say the map
. Similarly, we say the map  is a nonnegative continuous convex functional on a cone of a real Banach space
is a nonnegative continuous convex functional on a cone of a real Banach space  provided that
provided that  is continuous and
is continuous and

for all  and
and  .
.
Let  and
and  be a nonnegative continuous convex functionals on
be a nonnegative continuous convex functionals on  ,
,  a nonnegative continuous concave functional on
a nonnegative continuous concave functional on  , and
, and  a nonnegative continuous functional on
a nonnegative continuous functional on  . Then for positive real number
. Then for positive real number  , and
, and  , we define the following convex sets:
, we define the following convex sets:

Theorem 2.8 (see [11]).
Let  be a real Banach space and
be a real Banach space and  a cone. Assume that
a cone. Assume that  and
and  are two bounded open sets in
are two bounded open sets in  with
with  ,
,  . Let
. Let  be completely continuous. Suppose that one of following two conditions is satisfied:
be completely continuous. Suppose that one of following two conditions is satisfied:
(1) ,
,  , and
, and  ,
,  ;
;
(2) ,
,  , and
, and  ,
,  .
.
Then  has at least one fixed point in
has at least one fixed point in  .
.
Theorem 2.9 (see [12]).
Let  be a cone in a real Banach space
be a cone in a real Banach space  . Let
. Let  and
and  be a nonnegative continuous convex functionals on
be a nonnegative continuous convex functionals on  ,
,  a nonnegative continuous concave functional on
a nonnegative continuous concave functional on  , and
, and  a nonnegative continuous functional on
a nonnegative continuous functional on  satisfying
satisfying  for
for  , such that for positive number
, such that for positive number  and
and  ,
,

for all  . Suppose
. Suppose  is completely continuous and there exist positive numbers
is completely continuous and there exist positive numbers  , and
, and  with
with  such that
such that
 and
and  for
for  ;
;
() for
for  with
with  ;
;
() and
and  for
for  with
with  .
.
Then  has at least three fixed points
has at least three fixed points  , such that
, such that
 for
for  ,
,
 ,
,
 with
with  ,
,
 .
.
3. The Existence of One or Two Positive Solutions
For convenience, we denote

where  denotes 0 or
denotes 0 or  .
.
Theorem 3.1.
Assume that (H1) and (H2) hold. In addition, suppose that one of following conditions is satisfied.
-
(i)
There exist two constants
 with
with 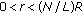 such that
such that
(a) for
for  and
and
(b) for
for  ;
;
(ii) ;
;
(iii) .
.
Then BVP(1.1) has at least one positive solution.
Proof.
-
(i)
Let
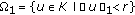 ,
, 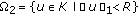 .
.
For  , we obtain
, we obtain  and
and  , which implies
, which implies  . Hence, by (2.12) and Lemma 2.6,
. Hence, by (2.12) and Lemma 2.6,

This implies that

Next, for  , we have
, we have  . Thus, by (2.12) and Lemma 2.6,
. Thus, by (2.12) and Lemma 2.6,

From (2.13), we have

This implies that

Therefore, by Theorem 2.8, it follows that  has a fixed point in
has a fixed point in  . That is BVP(1.1) has at least one positive solution such that
. That is BVP(1.1) has at least one positive solution such that  .
.
-
(ii)
Considering
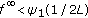 , there exists
, there exists 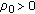 such that
such that  (3.7)
(3.7)
Choosing  such that
such that

then for all  , let
, let  . For every
. For every  , we have
, we have  . In the following, we consider two cases.
. In the following, we consider two cases.
Case 1 ( ).
).
In this case,

Case 2 ( ).
).
In this case,

Then it is similar to the proof of (3.6); we have  for
for  .
.
Next, turning to  , there exists
, there exists  such that
such that

Let  . For every
. For every  , we have
, we have  . So
. So

Then like in the proof of (3.3), we have  for
for  . Hence, BVP(1.1) has at least one positive solution such that
. Hence, BVP(1.1) has at least one positive solution such that  .
.
-
(iii)
The proof is similar to the (i) and (ii); here we omit it.
In the following, we present a result for the existence of at least two positive solutions of BVP(1.1).
Theorem 3.2.
Assume that (H1) and (H2) hold. In addition, suppose that one of following conditions is satisfied.
(I) ,
,  , and there exists
, and there exists  such that
such that

(II) ,
,  , and there exists
, and there exists  such that
such that

Then BVP(1.1) has at least two positive solutions.
4. The Existence of Three Positive Solutions
In this section, we impose growth conditions on  which allow us to apply Theorem 2.9 of BVP(1.1).
which allow us to apply Theorem 2.9 of BVP(1.1).
Let the nonnegative continuous concave functional  , the nonnegative continuous convex functionals
, the nonnegative continuous convex functionals  ,
,  , and nonnegative continuous functional
, and nonnegative continuous functional  be defined on cone
be defined on cone  by
by

By Lemmas 2.1 and 2.2, the functionals defined above satisfy

for all  . Therefore, the condition (2.19) of Theorem 2.9 is satisfied.
. Therefore, the condition (2.19) of Theorem 2.9 is satisfied.
Theorem 4.1.
Assume that (H1) and (H2) hold. Let  and suppose that
and suppose that  satisfies the following conditions:
satisfies the following conditions:
 for
for  ;
;
 for
for  .
.
 for
for  ;
;
Then BVP(1.1) has at least three positive solutions  , and
, and  satisfying
satisfying

where  defined as (3.1),
defined as (3.1),  .
.
Proof.
We will show that all the conditions of Theorem 2.9 are satisfied.
If  , then
, then  . With Lemma 2.2 implying
. With Lemma 2.2 implying  , so by (
, so by ( ), we have
), we have  when
when  . Thus
. Thus

This proves that  .
.
To check condition ( ) of Theorem 2.9, we choose
) of Theorem 2.9, we choose

Let

Then  and
and  , so
, so  . Hence, for
. Hence, for  , there is
, there is  ,
,  when
when  . From assumption (
. From assumption ( ), we have
), we have

It is similar to the proof of assumption (i) of Theorem 3.1; we can easily get that

This shows that condition ( ) of Theorem 2.9 is satisfied.
) of Theorem 2.9 is satisfied.
Secondly, for  with
with  , we have
, we have

Thus condition ( ) of Theorem 2.9 holds.
) of Theorem 2.9 holds.
Finally, as  , there holds
, there holds  . Suppose that
. Suppose that  with
with  ; then by the assumption (
; then by the assumption ( ),
),

So like in the proof of assumption (i) of Theorem 3.1, we can get

Hence condition ( ) of Theorem 2.9 is also satisfied.
) of Theorem 2.9 is also satisfied.
Thus BVP(1.1) has at least three positive solutions  , and
, and  satisfying
satisfying

5. Examples
In this section, we give three examples as applications.
Example 5.1.
Let  ,
,  . Now we consider the BVP
. Now we consider the BVP

where  for
for  .
.
Let  ,
,  . Choosing
. Choosing  . By calculations we obtain
. By calculations we obtain

For  ,
,

for  ,
,

Hence, by Theorem 3.1, BVP(5.1) has at least one positive solution.
Example 5.2.
Let  ,
,  . Consider the BVP
. Consider the BVP

where  for
for  .
.
Let  ,
,  . Then
. Then  . It easy to see
. It easy to see

Choosing  , for
, for  ,
,  .
.

Hence, by Theorem 3.2, BVP(5.5) has at least two positive solutions.
Example 5.3.
Let  ,
,  ; consider the boundary value problem
; consider the boundary value problem

where

Choosing  ,
,  ,
,  ,
,  , then by calculations we obtain that
, then by calculations we obtain that

It is easy to check that

Thus, according to Theorem 4.1, BVP(5.8) has at least three positive solutions  , and
, and  satisfying
satisfying

References
Wang H: On the number of positive solutions of nonlinear systems. Journal of Mathematical Analysis and Applications 2003, 281(1):287–306.
Wang H: On the structure of positive radial solutions for quasilinear equations in annular domains. Advances in Differential Equations 2003, 8(1):111–128.
Wang J: The existence of positive solutions for the one-dimensional p -Laplacian. Proceedings of the American Mathematical Society 1997, 125(8):2275–2283. 10.1090/S0002-9939-97-04148-8
Ji D, Ge W: Multiple positive solutions for some p -Laplacian boundary value problems. Applied Mathematics and Computation 2007, 187(2):1315–1325. 10.1016/j.amc.2006.09.041
Feng H, Ge W, Jiang M: Multiple positive solutions for m -point boundary-value problems with a one-dimensional p -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(8):2269–2279. 10.1016/j.na.2007.01.052
Liu B: Positive solutions of three-point boundary value problems for the one-dimensional p -Laplacian with infinitely many singularities. Applied Mathematics Letters 2004, 17(6):655–661. 10.1016/S0893-9659(04)90100-0
Wang Z, Zhang J: Positive solutions for one-dimensional p -Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006, 314(2):618–630. 10.1016/j.jmaa.2005.04.012
Yang Z: Existence and uniqueness of positive solutions for an integral boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(11):3910–3918. 10.1016/j.na.2007.10.026
Kong L: Second order singular boundary value problems with integral boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(5):2628–2638. 10.1016/j.na.2009.11.010
Boucherif A: Second-order boundary value problems with integral boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):364–371. 10.1016/j.na.2007.12.007
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Avery RI, Peterson AC: Three positive fixed points of nonlinear operators on ordered Banach spaces. Computers & Mathematics with Applications 2001, 42(3–5):313–322.
Acknowledgments
The research was supported by NNSF of China (10871160), the NSF of Gansu Province (0710RJZA103), and Project of NWNU-KJCXGC-3-47.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ding, Y. Positive Solutions for Integral Boundary Value Problem with ϕ-Laplacian Operator. Bound Value Probl 2011, 827510 (2011). https://doi.org/10.1155/2011/827510
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/827510
 with
with 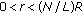 such that
such that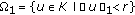 ,
, 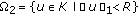 .
.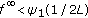 , there exists
, there exists 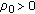 such that
such that 