- Research Article
- Open access
- Published:
On the Derivatives of Bernstein Polynomials: An Application for the Solution of High Even-Order Differential Equations
Boundary Value Problems volume 2011, Article number: 829543 (2011)
Abstract
A new formula expressing explicitly the derivatives of Bernstein polynomials of any degree and for any order in terms of Bernstein polynomials themselves is proved, and a formula expressing the Bernstein coefficients of the general-order derivative of a differentiable function in terms of its Bernstein coefficients is deduced. An application of how to use Bernstein polynomials for solving high even-order differential equations by Bernstein Galerkin and Bernstein Petrov-Galerkin methods is described. These two methods are then tested on examples and compared with other methods. It is shown that the presented methods yield better results.
1. Introduction
Bernstein polynomials [1] have many useful properties, such as, the positivity, the continuity, and unity partition of the basis set over the interval  . The Bernstein polynomial bases vanish except the first polynomial at
. The Bernstein polynomial bases vanish except the first polynomial at  , which is equal to 1 and the last polynomial at
, which is equal to 1 and the last polynomial at  , which is also equal to 1 over the interval
, which is also equal to 1 over the interval  . This provides greater flexibility in imposing boundary conditions at the end points of the interval. The moments
. This provides greater flexibility in imposing boundary conditions at the end points of the interval. The moments  is nothing but Bernstein polynomial itself. With the advent of computer graphics, Bernstein polynomial restricted to the interval
is nothing but Bernstein polynomial itself. With the advent of computer graphics, Bernstein polynomial restricted to the interval  becomes important in the form of Bezier curves [2]. Many properties of the Bézier curves and surfaces come from the properties of the Bernstein polynomials. Moreover, Bernstein polynomials have been recently used for the solution of differential equations, (see, e.g., [3]).
becomes important in the form of Bezier curves [2]. Many properties of the Bézier curves and surfaces come from the properties of the Bernstein polynomials. Moreover, Bernstein polynomials have been recently used for the solution of differential equations, (see, e.g., [3]).
The Bernstein polynomials are not orthogonal; so their uses in the least square approximations are limited. To overcome this difficulty, two approaches are used. The first approach is the basis transformation, for the transformation matrix between Bernstein polynomial basis and Legendre polynomial basis [4], between Bernstein polynomial basis and Chebyshev polynomial basis [5], and between Bernstein polynomial basis and Jacobi polynomial basis [6]. The second approach is the dual basis functions for Bernstein polynomials (see Jüttler [7]). Jüttler [7] derived an explicit formula for the dual basis function of Bernstein polynomials. The construction of the dual basis must be repeated at each time the approximation polynomial increased.
For spectral methods [8, 9], explicit formulae for the expansion coefficients of a general-order derivative of an infinitely differentiable function in terms of those of the original expansion coefficients of the function itself are needed. Such formulae are available for expansions in Chebyshev [10], Legendre [11], ultraspherical [12], Hermite [13], Jacobi [14], and Laguerre [15] polynomials. These polynomials have been used in both the solution of boundary value problems [16–19] and in computational fluid dynamics [8]. In most of these applications, use is made of formulae relating the expansion coefficients of derivatives appearing in the differential equation to those of the function itself, (see, e.g., [16–19]). This process results in an algebraic system or a system of differential equations for the expansion coefficients of the solution which then must be solved.
Due to the increasing interest on Bernstein polynomials, the question arises of how to describe their properties in terms of their coefficients when they are given in the Bernstein basis. Up to now, and to the best of our Knowledge, many formulae corresponding to those mentioned previously are unknown and are traceless in the literature for Bernstein polynomials. This partially motivates our interest in such polynomials.
Another motivation is concerned with the direct solution techniques for solving high even-order differential equations, using the Bernstein Galerkin approximation. Also, we use Bernstein Petrov-Galerkin approximation; we choose the trial functions to satisfy the underlying boundary conditions of the differential equations, and the test functions to be dual Bernstein polynomials which satisfy the orthogonality condition. The method leads to linear systems which are sparse for problems with constant coefficients. Numerical results are presented in which the usual exponential convergence behavior of spectral approximations is exhibited.
The remainder of this paper is organized as follows. In Section 2, we give an overview of Bernstein polynomials and the relevant properties needed in the sequel, and in Section 3, we prove the main results of the paper which are: (i) an explicit expression for the derivatives of Bernstein polynomials of any degree and for any order in terms of the Bernstein polynomials themselves and (ii) an explicit formula for the expansion coefficient of the derivatives of an infinitely differentiable function in terms of those of the original expansion coefficients of the functions itself. In Section 4, we discuss separately Bernstein Galerkin and Bernstein Petrov-Galerkin methods and describe how they are used to solve high even-order differential equations. Finally, Section 5 gives some numerical results exhibiting the accuracy and efficiency of our proposed numerical algorithms.
2. Relevant Properties of Bernstein Polynomials
The Bernstein polynomials of  th degree form a complete basis over
th degree form a complete basis over  , and they are defined by
, and they are defined by

where the binomial coefficients are given by  .
.
The derivatives of the  th degree Bernstein polynomials are polynomials of degree
th degree Bernstein polynomials are polynomials of degree  and are given by
and are given by

The multiplication of two Bernstein basis is

and the moments of Bernstein basis are

Like any basis of the space  , the Bernstein polynomials have a unique dual basis
, the Bernstein polynomials have a unique dual basis  (also called the inverse or reciprocal basis) which consists of the
(also called the inverse or reciprocal basis) which consists of the  dual basis functions
dual basis functions

where

Jüttler [7] represented the dual basis function with respect to the Bernstein basis. The dual basis functions must satisfy the relation of duality

Indefinite integral of Bernstein basis is given by

and all Bernstein basis function of the same order have the same definite integral over the interval  , namely,
, namely,

3. Derivatives of Bernstein Polynomials
The main objective of this section is to prove the following two theorems for the derivatives of  and Bernstein coefficients of the
and Bernstein coefficients of the  th derivative of
th derivative of  .
.
Theorem 3.1.

Proof.
For  , (3.1) leads us to go back to (2.2).
, (3.1) leads us to go back to (2.2).
If we apply induction on  , assuming that (3.1) holds, we want to show that
, assuming that (3.1) holds, we want to show that

If we differentiate (3.1), then we have (with application of relation (2.2))

which can be written as

Set  in the first term of the right-hand side of relation (3.4) to get
in the first term of the right-hand side of relation (3.4) to get

It can be easily shown that

which completes the induction and proves the theorem.
We can express the Bernstein polynomial of any degree  in terms of any higher degree basis
in terms of any higher degree basis  using the following lemma.
using the following lemma.
Lemma 3.2.

For proof, see, Farouki and Rajan [20].
Let  be a differentiable function of degree
be a differentiable function of degree  defined on the interval
defined on the interval  , then we can write
, then we can write

Further, let  denote the Bernstein coefficients of the
denote the Bernstein coefficients of the  th derivative of
th derivative of  , that is,
, that is,

Then, we can state and prove the following theorem.
Theorem 3.3.

where

Proof.
Since

then making use of Theorem 3.1 (formula (3.1)) immediately yields

If we change the degree of Bernstein polynomials using (3.7), then we can write

Expanding the two summation  and rearranging the coefficients of
and rearranging the coefficients of  from
from  , we get
, we get

and this completes the proof of Theorem 3.3.
The following two corollaries will be of fundamental importance in what follows.
Corollary 3.4.

Proof.
We can express explicitly the  th derivatives of Bernstein polynomials from Theorem 3.1 to obtain
th derivatives of Bernstein polynomials from Theorem 3.1 to obtain

Now, (3.16) can be easily derived by using (2.3). Thanks to (2.9), we have

Corollary 3.5.

Proof.
Using Theorem 3.1, we get

It follows immediately from (3.7) and (2.7) that

4. An Application for the Solution of High Even-Order Differential Equations
4.1. Bernstein Galerkin Method
Consider the solution of the differential equation

subject to the following boundary conditions

Let us first introduce some basic notation which will be used in the sequel. We set

then the Bernstein-Galerkin approximation to (4.1) is to find  such that
such that

where  is the inner product in
is the inner product in  , and its norm will be denoted by
, and its norm will be denoted by  .
.
It is of fundamental importance to note here that the crucial task in applying the Galerkin-spectral Bernstein approximations is how to choose an appropriate basis for  such that the linear system resulting from the Bernstein-Galerkin approximation to (4.4) is as simple as possible.
such that the linear system resulting from the Bernstein-Galerkin approximation to (4.4) is as simple as possible.
We can choose the basis functions  to be of the form
to be of the form

where 

 for all
for all  . The
. The  boundary conditions lead to the first
boundary conditions lead to the first  and the last
and the last  expansion coefficients to be zero.
expansion coefficients to be zero.
Therefore, for  , we have
, we have

It is now clear that (4.4) is equivalent to

Let us denote

Then, (4.7) is equivalent to the following matrix equation

where the elements of the matrices  ,
,  , and
, and  ,
,  are given explicitly using Corollary 3.4, as follows:
are given explicitly using Corollary 3.4, as follows:

4.2. Bernstein Petrov-Galerkin Method
The Petrov-Galerkin method generates a sequence of approximate solutions that satisfy a weak form of the original differential equation as tested against polynomials in a dual space. To describe this method and the full discretization more precisely, we introduce some basic notation. We set

Denoting by  and
and  the spaces of Bernstein polynomials of degree ≤
the spaces of Bernstein polynomials of degree ≤ and dual Bernstein of degree ≤
and dual Bernstein of degree ≤ , then the Bernstein Petrov-Galerkin approximation to (4.1) is, to find
, then the Bernstein Petrov-Galerkin approximation to (4.1) is, to find  such that
such that

We choose the trial Bernstein functions to satisfy the underlying boundary conditions of the differential equation, and we choose the test dual Bernstein functions to satisfy the orthogonality condition. Consider the test and trial functions of expansion  and
and  to be of the form
to be of the form

where 

 and
and 

 , for all
, for all  . The
. The  boundary conditions lead to the first
boundary conditions lead to the first  and the last
and the last  expansion coefficients to be zero.
expansion coefficients to be zero.
Therefore, for  , we have
, we have

and, accordingly, (4.12) is equivalent to

Let us denote

Then, (4.15) is equivalent to the following matrix equation:

If we take  and
and  as defined in (4.13) and if we denote
as defined in (4.13) and if we denote  and
and  . Then, the elements
. Then, the elements  ,
,  , and
, and  for
for  ,
,  are given explicitly by using Corollary 3.5, as follows:
are given explicitly by using Corollary 3.5, as follows:

4.3. Using Coefficients of Differentiated Expansions
Here, we shall use Theorem 3.3 for the solution of the  th-order differential (4.1)-(4.2). We approximate
th-order differential (4.1)-(4.2). We approximate  by an expansion of Bernstein polynomials
by an expansion of Bernstein polynomials

We seek to determine  ,
,  , using Petrov-Galerkin method. Note here that we set
, using Petrov-Galerkin method. Note here that we set  ,
,  to ensure that the boundary conditions (4.2) are satisfied. Since
to ensure that the boundary conditions (4.2) are satisfied. Since  and
and  are polynomials of degree at most
are polynomials of degree at most  and
and  , respectively, we may write
, respectively, we may write

where

It is to be noted here that (4.21) is obtained by making use of relation (3.11). The coefficients  are chosen so that
are chosen so that  satisfies
satisfies

Substituting (4.19) and (4.20) into (4.22), multiplying by  , and integrating over the interval
, and integrating over the interval  yield
yield

where

Thus, there are  equations for the
equations for the  unknowns
unknowns  , in order to obtain a solution; it is only necessary to solve (4.23) with the help of (4.21) for the
, in order to obtain a solution; it is only necessary to solve (4.23) with the help of (4.21) for the  unknowns coefficients
unknowns coefficients  ,
,  .
.
5. Numerical Results
We solve in this section several numerical examples by using the algorithms presented in the previous section. Comparisons between Bernstein Galerkin method (BGM), Bernstein Petrov-Galerkin method (BPGM), and other methods proposed in [21–24] are made. We consider the following examples.
Example 5.1.
Consider the boundary value problem (see, [22])

subject to the boundary conditions  , with the exact solution
, with the exact solution  .
.
Table 1 lists the maximum pointwise error  and maximum absolute relative error
and maximum absolute relative error  of
of  using the BGM and BPGM with various choices of
using the BGM and BPGM with various choices of  . Table 1 shows that our methods have better accuracy compared with the quintic nonpolynomial spline method developed in [22]; it is also shown that, in the case of solving linear system of order 14, we obtain a maximum absolute error of order
. Table 1 shows that our methods have better accuracy compared with the quintic nonpolynomial spline method developed in [22]; it is also shown that, in the case of solving linear system of order 14, we obtain a maximum absolute error of order  . It is worthy noting here that the method of [22] gives the maximum absolute error
. It is worthy noting here that the method of [22] gives the maximum absolute error  but by solving a linear system of order 64 instead of order 14 in our case.
but by solving a linear system of order 64 instead of order 14 in our case.
 and
and  for
for  .
.Example 5.2.
We consider the fourth-order two point boundary value problem (see, [21])

with the analytical solution  .
.
Table 2 lists the maximum pointwise error and maximum absolute relative error of  using the BGM and BPGM with various choices of
using the BGM and BPGM with various choices of  . In Table 3, a comparison between the error obtained by using BGM, BPGM, the sinc-Galerkin, and modified decomposition methods (see, [21]) is displayed. This definitely shows that our methods are more accurate.
. In Table 3, a comparison between the error obtained by using BGM, BPGM, the sinc-Galerkin, and modified decomposition methods (see, [21]) is displayed. This definitely shows that our methods are more accurate.
 and
and  for
for  .
.Example 5.3.
Consider the sixth-order BVP (see, [21, 23, 24])

with the exact solution  .
.
Table 4 lists the maximum pointwise error and maximum absolute relative error of  using BGM and BPG with various choices of
using BGM and BPG with various choices of  . Table 5 exhibits a comparison between the error obtained by using BGM, BPGM, and Sinc-Galerkin in [21], septic splines in [23] and modified decomposition in [24]. From this Table, one can check that our methods are more accurate.
. Table 5 exhibits a comparison between the error obtained by using BGM, BPGM, and Sinc-Galerkin in [21], septic splines in [23] and modified decomposition in [24]. From this Table, one can check that our methods are more accurate.
 and
and  for
for  .
.References
Lorentz GG: Bernstein Polynomials, Mathematical Expositions, no. 8. University of Toronto Press, Toronto, Canada; 1953:x+130.
Farin G: Curves and Surfaces for Computer Aided Geometric Design. Academic Press, Boston, Mass, USA; 1996.
Bhatti MI, Bracken P: Solutions of differential equations in a Bernstein polynomial basis. Journal of Computational and Applied Mathematics 2007, 205(1):272–280. 10.1016/j.cam.2006.05.002
Boyd JP: Exploiting parity in converting to and from Bernstein polynomials and orthogonal polynomials. Applied Mathematics and Computation 2008, 198(2):925–929.
Rababah A: Transformation of Chebyshev-Bernstein polynomial basis. Computational Methods in Applied Mathematics 2003, 3(4):608–622.
Rababah A: Jacobi-Bernstein basis transformation. Computational Methods in Applied Mathematics 2004, 4(2):206–214.
Jüttler B: The dual basis functions for the Bernstein polynomials. Advances in Computational Mathematics 1998, 8(4):345–352. 10.1023/A:1018912801267
Canuto C, Hussaini MY, Quarteroni A, Zang TA: Spectral Methods in Fluid Mechanics, Scientific Computation. Springer, Berlin, Germany; 1988:xxii+563.
Livermore PW: Orthogonal Galerkin polynomials. Journal of Computational Physics 2010, 229(6):2046–2060. 10.1016/j.jcp.2009.11.022
Karageorghis A: A note on the Chebyshev coefficients of the general order derivative of an infinitely differentiable function. Journal of Computational and Applied Mathematics 1988, 21(1):129–132. 10.1016/0377-0427(88)90396-2
Phillips TN: On the Legendre coefficients of a general-order derivative of an infinitely differentiable function. IMA Journal of Numerical Analysis 1988, 8(4):455–459. 10.1093/imanum/8.4.455
Karageorghis A, Phillips TN: On the coefficients of differentiated expansions of ultraspherical polynomials. Applied Numerical Mathematics 1992, 9(2):133–141. 10.1016/0168-9274(92)90010-B
Doha EH: On the connection coefficients and recurrence relations arising from expansions in series of Hermite polynomials. Integral Transforms and Special Functions 2004, 15(1):13–29. 10.1080/10652460310001600618
Doha EH: On the construction of recurrence relations for the expansion and connection coefficients in series of Jacobi polynomials. Journal of Physics. A 2004, 37(3):657–675. 10.1088/0305-4470/37/3/010
Doha EH: On the connection coefficients and recurrence relations arising from expansions in series of Laguerre polynomials. Journal of Physics. A 2003, 36(20):5449–5462. 10.1088/0305-4470/36/20/307
Doha EH, Bhrawy AH: Efficient spectral-Galerkin algorithms for direct solution for second-order differential equations using Jacobi polynomials. Numerical Algorithms 2006, 42(2):137–164. 10.1007/s11075-006-9034-6
Doha EH, Bhrawy AH: Efficient spectral-Galerkin algorithms for direct solution of fourth-order differential equations using Jacobi polynomials. Applied Numerical Mathematics 2008, 58(8):1224–1244. 10.1016/j.apnum.2007.07.001
Doha EH, Bhrawy AH: A Jacobi spectral Galerkin method for the integrated forms of fourth-order elliptic differential equations. Numerical Methods for Partial Differential Equations 2009, 25(3):712–739. 10.1002/num.20369
Doha EH, Bhrawy AH, Abd-Elhameed WM: Jacobi spectral Galerkin method for elliptic Neumann problems. Numerical Algorithms 2009, 50(1):67–91. 10.1007/s11075-008-9216-5
Farouki RT, Rajan VT: Algorithms for polynomials in Bernstein form. Computer Aided Geometric Design 1988, 5(1):1–26. 10.1016/0167-8396(88)90016-7
El-gamel M: A comparison between the sinc-Galerkin and the modified decomposition methods for solving two-point boundary-value problems. Journal of Computational Physics 2007, 223(1):369–383. 10.1016/j.jcp.2006.09.025
Ramadan MA, Lashien IF, Zahra WK: High order accuracy nonpolynomial spline solutions for
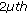 order two point boundary value problems. Applied Mathematics and Computation 2008, 204(2):920–927. 10.1016/j.amc.2008.07.038
order two point boundary value problems. Applied Mathematics and Computation 2008, 204(2):920–927. 10.1016/j.amc.2008.07.038Siddiqi SS, Akram G: Septic spline solutions of sixth-order boundary value problems. Journal of Computational and Applied Mathematics 2008, 215(1):288–301. 10.1016/j.cam.2007.04.013
Wazwaz A: The numerical solution of sixth-order boundary value problems by the modified decomposition method. Applied Mathematics and Computation 2001, 118(2–3):311–325. 10.1016/S0096-3003(99)00224-6
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Doha, E., Bhrawy, A. & Saker, M. On the Derivatives of Bernstein Polynomials: An Application for the Solution of High Even-Order Differential Equations. Bound Value Probl 2011, 829543 (2011). https://doi.org/10.1155/2011/829543
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/829543
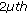 order two point boundary value problems. Applied Mathematics and Computation 2008, 204(2):920–927. 10.1016/j.amc.2008.07.038
order two point boundary value problems. Applied Mathematics and Computation 2008, 204(2):920–927. 10.1016/j.amc.2008.07.038