- Review Article
- Open access
- Published:
An Overview of the Lower and Upper Solutions Method with Nonlinear Boundary Value Conditions
Boundary Value Problems volume 2011, Article number: 893753 (2011)
Abstract
The aim of this paper is to point out recent and classical results related with the existence of solutions of second-order problems coupled with nonlinear boundary value conditions.
1. Introduction
The first steps in the theory of lower and upper solutions have been given by Picard in 1890 [1] for Partial Differential Equations and, three years after, in [2] for Ordinary Differential Equations. In both cases, the existence of a solution is guaranteed from a monotone iterative technique. Existence of solutions for Cauchy equations have been proved by Perron in 1915 [3]. In 1927, Müller extended Perron's results to initial value systems in [4].
Dragoni [5] introduces in 1931 the notion of the method of lower and upper solutions for ordinary differential equations with Dirichlet boundary value conditions. In particular, by assuming stronger conditions than nowadays, the author considers the second-order boundary value problem

for  a continuous function and
a continuous function and  .
.
The most usual form to define a lower solution is to consider a function  that satisfies the inequality
that satisfies the inequality

together with

In the same way, an upper solution is a function  that satisfies the reversed inequalities
that satisfies the reversed inequalities


When  on
on  , the existence of a solution of the considered problem lying between
, the existence of a solution of the considered problem lying between  and
and  is proved.
is proved.
In consequence, this method allows us to ensure the existence of a solution of the considered problem lying between the lower and the upper solution, that is, we have information about the existence and location of the solutions. So the problem of finding a solution of the considered problem is replaced by that of finding two well-ordered functions that satisfy some suitable inequalities.
Following these pioneering results, there have been a large number of works in which the method has been developed for different kinds of boundary value problems, thus first-, second- and higher-order ordinary differential equations with different type of boundary conditions such as, among others, periodic, mixed, Dirichlet, or Neumann conditions, have been considered. Also partial differential equations of first and second-order, have been treated in the literature.
In these situations, we have that for the Neumann problem

a lower solution  is a
is a  -function that satisfies (1.2) coupled with the inequalities
-function that satisfies (1.2) coupled with the inequalities

 is an upper solution of the Neumann problem if it satisfies (1.4) and
is an upper solution of the Neumann problem if it satisfies (1.4) and

Analogously, for the periodic problem

a lower solution  and an upper solution
and an upper solution  are
are  -functions that satisfy (1.2) and (1.4), respectively, together with the inequalities
-functions that satisfy (1.2) and (1.4), respectively, together with the inequalities

In the classical books of Bernfeld and Lakshmikantham [6] and Ladde et al. [7] the classical theory of the method of lower and upper solutions and the monotone iterative technique are given. This gives the solution as the limit of a monotone sequence formed by functions that solve linear problems related to the nonlinear equations considered. We refer the reader to the classical works of Mawhin [8–11] and the surveys in this field of De Coster and Habets [12–14] in which one can found historical and bibliographical references together with recent results and open problems.
It is important to point out that to derive the existence of a solution a growth condition on the nonlinear part of the equation with respect to the dependence on the first derivative is imposed. The most usual condition is the so-called Nagumo condition that was introduced for this author [15] in 1937. This condition imposes, roughly speaking, a quadratic growth in the dependence of the derivative. The most common form of presenting it is the following.
Definition 1.1.
We say that  satisfies the Nagumo condition if there is
satisfies the Nagumo condition if there is  satisfying
satisfying


with  .
.
The main importance of this condition is that it provides a priori bounds on the first derivative of all the possible solutions of the studied problem that lie between the lower and the upper solution. A careful proof of this property has been made in [6]. One can verify that in the proof the condition (1.12) can be replaced by the weaker one,

The usual tool to derive an existence result consists in the construction of a modified problem that satisfies the two following properties.
()The nonlinear part of the modified equation is bounded.
()The nonlinear part of the modified equation coincides with the nonlinear part when the spatial variable is in  .
.
When the Dirichlet problem (1.1) is studied, the usual truncated problem considered is

Here


with

Notice that both  and
and  are continuous and bounded functions and, in consequence, if
are continuous and bounded functions and, in consequence, if  is continuous, both properties are satisfied by
is continuous, both properties are satisfied by  .
.
In the proof it is deduced that all the solutions  of the truncated problem (1.14) belong to the segment
of the truncated problem (1.14) belong to the segment  and
and  on
on  . Notice that the constant
. Notice that the constant  only depends on
only depends on  ,
,  and
and  . The existence of solutions is deduced from fixed point theory.
. The existence of solutions is deduced from fixed point theory.
It is important to point out that the a priori bound is deduced for all solutions of the truncated problem. The boundary data is not used. This property is fundamental when more general situations are considered.
In 1954, Nagumo [16] constructed an example in which the existence of well-ordered lower and upper solutions is not sufficient to ensure the existence of solutions of a Dirichlet problem, that is, in general this growth condition cannot be removed for the Dirichlet case. An analogous result concerning the optimality of the Nagumo condition for periodic and Sturm-Liouville conditions has been showed recently by Habets and Pouso in [17].
In 1967, Kiguradze [18] proved that it is enough to consider a one-sided Nagumo condition (by eliminating the absolute value in (1.11)) to deduce existence results for Dirichlet problems. Similar results have been given in 1968 by Schrader [19].
Other classical assumptions that impose some growth conditions on the nonlinear part of the equation are given in 1939 by Tonelli [20]. In this situation, considering the Dirichlet problem (1.1) with  , the following one-sided growth condition is assumed:
, the following one-sided growth condition is assumed:

where  and
and  are sufficiently small numbers.
are sufficiently small numbers.
Different generalizations of these conditions have been developed by, among others, Epheser [21], Krasnoselskii [22], Kiguradze [23, 24], Mawhin [25], and Fabry and Habets [26].
In the case of  being a Carathéodory function, the arguments to deduce the existence result are not a direct translation from the continuous case. This is due to the fact that in the proof the properties are fulfilled at every point of the interval
being a Carathéodory function, the arguments to deduce the existence result are not a direct translation from the continuous case. This is due to the fact that in the proof the properties are fulfilled at every point of the interval  . In this new situation the equalities and inequalities hold almost everywhere and, in consequence, the arguments must be directed to positive measurable sets. Thus, a suitable truncated problem is the following:
. In this new situation the equalities and inequalities hold almost everywhere and, in consequence, the arguments must be directed to positive measurable sets. Thus, a suitable truncated problem is the following:

coupled with the corresponding boundary value conditions.
This truncation has been introduced by Gao and Wang in [27] for the periodic problem and improves a previous one given by Wang et al. in [28]. Notice that the function  is bounded in
is bounded in  and it is measurable because of the following result proved in [28, Lemma
and it is measurable because of the following result proved in [28, Lemma  ].
].
Lemma 1.2.
For any  , the two following properties hold:
, the two following properties hold:
(a) exists for a.e.
exists for a.e.  ;
;
(b)If  and
and  , then
, then  for a.e.
for a.e.  .
.
When a one-sided Lipschitz condition of the following type:

is assumed on function  for some
for some  and all
and all  , it is possible to deduce the existence of extremal solutions in the sector
, it is possible to deduce the existence of extremal solutions in the sector  of the considered problem. By extremal solutions we mean the greatest and the smallest solutions in the set of all the solutions in
of the considered problem. By extremal solutions we mean the greatest and the smallest solutions in the set of all the solutions in  . The deduction of such a property holds from an iterative technique that consists of solving related linear problems on
. The deduction of such a property holds from an iterative technique that consists of solving related linear problems on  and using suitable maximum principles which are equivalent to the constant sign of the associated Green's function. One can find in [7] a complete development of this theory for different kinds of boundary value conditions.
and using suitable maximum principles which are equivalent to the constant sign of the associated Green's function. One can find in [7] a complete development of this theory for different kinds of boundary value conditions.
It is important to note that there are many papers that have tried to get existence results under weaker assumptions on the definition of lower and upper solutions. In particular, Scorza Dragoni proves in 1938 [29], an existence result for the Dirichlet problem by assuming the existence of two  functions
functions  that satisfy
that satisfy

are nondecreasing in  .
.
Kiguradze uses in [24] regular lower and upper solutions and explain that it is possible to get the same results for lower and upper solutions whose first derivatives are not absolutely continuous functions. Ponomarev considers in [30] two continuous functions  with right Dini derivatives
with right Dini derivatives  , absolute semicontinuous from below in
, absolute semicontinuous from below in  , and
, and  absolute semicontinuous from above in
absolute semicontinuous from above in  , that satisfy the following inequalities a.e.
, that satisfy the following inequalities a.e.  :
:

For further works in this direction see [31–36].
Cherpion et al. prove in [37] the existence of extremal solutions for the Dirichlet problem without assuming the condition (1.20). In fact, they consider a more general problem: the  -laplacian equation. In this case, they define a concept of lower and upper solutions in which some kind of angles are allowed. The definitions are the following.
-laplacian equation. In this case, they define a concept of lower and upper solutions in which some kind of angles are allowed. The definitions are the following.
Definition 1.3.
A function  is a lower solution of problem (1.1) (with
is a lower solution of problem (1.1) (with  ), if
), if  ,
,  , and for any
, and for any  , either
, either  , or there exists an open interval
, or there exists an open interval  such that
such that  ,
,  and, for a.e.
and, for a.e.  ,
,

Definition 1.4.
A function  is a lower solution of problem (1.1) (with
is a lower solution of problem (1.1) (with  ), if
), if  ,
,  , and for any
, and for any  , either
, either  , or there exists an open interval
, or there exists an open interval  such that
such that  ,
,  and, for a.e.
and, for a.e.  ,
,

Here  ,
,  ,
,  , and
, and  denote the usual Dini derivatives.
denote the usual Dini derivatives.
By means of a sophisticated argument, the authors construct a sequence of upper solutions that converges uniformly to the function defined at each point  as the minimum value attained by all the solutions of problem (1.1) in
as the minimum value attained by all the solutions of problem (1.1) in  at this point. Passing to the limit, they conclude that such function is a solution too. The construction of these upper solutions is valid only in the case that corners are allowed in the definition. The same idea is valid to get a maximal solution.
at this point. Passing to the limit, they conclude that such function is a solution too. The construction of these upper solutions is valid only in the case that corners are allowed in the definition. The same idea is valid to get a maximal solution.
Similar results are deduced for the periodic boundary conditions in [12]. In this case the arguments follow from the finite intersection property of the set of solutions (see [38, 39]).
2. Two-Point Nonlinear Boundary Value Conditions
Two point nonlinear boundary conditions are considered with the aim of covering more complicated situations as, for instance,  or
or  .
.
In general, the framework of linear boundary conditions cannot be directly translated to this new situation. For instance, as we have noticed in the previous section, to ensure existence results for linear boundary conditions, we make use of the fixed point theory. So, in the case of a Dirichlet problem, the set of solutions of (1.1) coincide with the set of the fixed points of the operator  , defined by
, defined by

where

is the Green's function related to the linear problem

It is obvious that when nonlinear boundary value conditions are treated, the operator whose fixed points are the solutions of the considered problem must be modified.
Moreover the truncations that have to be made in the nonlinear part of the problem (1.14), for the continuous case, and in (1.19), for the Carathéodory one, must be extended to the nonlinear boundary conditions. This new truncation on the boundary conditions must satisfy similar properties to the ones of the nonlinear part of the equation, that is,
()the modified nonlinear boundary value conditions must be bounded,
()the modified nonlinear boundary value conditions coincide with the nonmodified ones in  .
.
So, to deduce existence results for this new situation, it is necessary to make use of the qualitative properties of continuity and monotonicity of the functions that define the nonlinear boundary value conditions.
Perhaps the first work that considers nonlinear boundary value conditions coupled with lower and upper solutions is due to Bebernes and Fraker [40] in 1971. In this work, the equation  coupled with the boundary conditions
coupled with the boundary conditions  and
and  is considered. Here,
is considered. Here,  is compact and connected and
is compact and connected and  is closed and connected. Under some additional conditions on the two sets, that include as a particular case
is closed and connected. Under some additional conditions on the two sets, that include as a particular case  ;
;  , the existence result is deduced under the assumption that a pair of well-ordered lower and upper solutions exist and a Nagumo condition is satisfied.
, the existence result is deduced under the assumption that a pair of well-ordered lower and upper solutions exist and a Nagumo condition is satisfied.
Later Bernfeld and Lakshmikantham [6] studied the boundary conditions  ; with
; with  and
and  monotone nonincreasing in the second variable.
monotone nonincreasing in the second variable.
Erbe considers in [41] the three types of boundary value conditions:

Here functions  and
and  satisfy suitable monotonicity conditions. Such monotonicity properties include, as particular cases, the periodic problem in the first situation and the separated conditions in the second and third cases.
satisfy suitable monotonicity conditions. Such monotonicity properties include, as particular cases, the periodic problem in the first situation and the separated conditions in the second and third cases.
The proofs follow from the study of the Dirichlet problem (1.1) with  and
and  . From the monotonicity assumptions it is proved, by a similar argument to the shooting method, that there is at least a pair
. From the monotonicity assumptions it is proved, by a similar argument to the shooting method, that there is at least a pair  ,
,  for which the boundary conditions hold.
for which the boundary conditions hold.
Mawhin studies in [11] the nonlinear separated boundary conditions

with  and
and  two nondecreasing functions in
two nondecreasing functions in  for all
for all  and
and  .
.
In this case, he constructs the modified problem

with  defined in (1.12) and
defined in (1.12) and  in (1.15).
in (1.15).
Virzhbitskiĭ and Sadyrbaev consider in [42] the conditions

where  is a continuously parametrized curve in
is a continuously parametrized curve in  and
and  is a continuous function. The proof is based on reducing the problem to another one with divided boundary conditions and applying the Bol'-Brauer theorem.
is a continuous function. The proof is based on reducing the problem to another one with divided boundary conditions and applying the Bol'-Brauer theorem.
Fabry and Habets treat in [26] the two types of boundary value conditions


with  , and
, and  monotone functions in some of their variables.
monotone functions in some of their variables.
The first case covers the periodic case and the second one separated boundary conditions.
In the proofs, a more general definition of lower and upper solutions is used. In particular, they replace the definitions (1.2) and (1.4) by the following ones.
 are continuous functions with right Dini derivatives
are continuous functions with right Dini derivatives  and
and  continuous from the right and left Dini derivatives
continuous from the right and left Dini derivatives  and
and  such that
such that
()for all  it is satisfied that
it is satisfied that  ,
,  and
and  ;
;
()the functions

are nondecreasing in  .
.
It is clear that if  and
and  are
are  -functions, this definition reduces to (1.2) and (1.4). Moreover, they assume a more general condition than the Nagumo one.
-functions, this definition reduces to (1.2) and (1.4). Moreover, they assume a more general condition than the Nagumo one.
To deduce existence results for (2.8) they consider a variant of the truncated problem (1.14) (by adding the term tanh ) coupled with the following nonconstant Dirichlet boundary conditions:
) coupled with the following nonconstant Dirichlet boundary conditions:

with  defined in (1.15).
defined in (1.15).
When the conditions (2.9) are studied, the authors consider

The proofs follow from oscillation theory and boundedness of the boundary conditions.
In [43], by using degree theory, Rachůnková proves the existence of at least two different solutions with boundary conditions

Here,  and
and  satisfy some suitable monotonicity conditions that cover as a particular case the separated ones.
satisfy some suitable monotonicity conditions that cover as a particular case the separated ones.
In all of the previous works,  is considered a continuous function.
is considered a continuous function.
For  being a Carathéodory function Sadyrbaev studies in [44, 45] the first-order system
being a Carathéodory function Sadyrbaev studies in [44, 45] the first-order system  ,
,  , coupled with boundary value conditions
, coupled with boundary value conditions  with
with  some suitable sets.
some suitable sets.
Lepin et al. generalize in [31, 34, 35] some of the results proved by Erbe in [41].
Adje generalizes in [46] the results obtained by Fabry and Habets in [26] for problem (2.8) and proves the existence of solution by considering the boundary value conditions

and  is a
is a  -Carathéodory function.
-Carathéodory function.
Franco and O'Regan, by avoiding some monotonicity assumptions on the boundary data, introduce in [47] a new definition of coupled lower and upper solutions for the boundary value conditions (2.9). In this case, the definition of such functions concerns both of the functions together. Under this definition they cover, under the same notation, periodic, antiperiodic, and Dirichlet boundary value conditions. Moreover they introduce a new concept of Nagumo condition as follows.
Definition 2.1.
One says that  satisfies a Nagumo condition relative to the interval
satisfies a Nagumo condition relative to the interval  , where
, where  is a lower solution and
is a lower solution and  is an upper solution if for
is an upper solution if for

there exists a constant  such that
such that

and a continuous function  such that
such that

3. 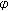 -Laplacian Problems and Functional Boundary Conditions
-Laplacian Problems and Functional Boundary Conditions
A more general framework of the second-order general equation  is given by the so-called
is given by the so-called  -laplacian equation. This kind of problems follow the expression
-laplacian equation. This kind of problems follow the expression

where  for some
for some  . This type of equations appears in the study of nonNewtonian fluid mechanics [48, 49].
. This type of equations appears in the study of nonNewtonian fluid mechanics [48, 49].
As far as the author is aware, the first reference in which this problem has been studied in combination with the method of lower and upper solutions is due to De Coster in [50], who considers (3.1) (without dependence on  ) coupled with Dirichlet conditions. Moreover, she treat, a more general operator
) coupled with Dirichlet conditions. Moreover, she treat, a more general operator  that includes, as a particular case, the
that includes, as a particular case, the  -laplacian operator. To be concise, operator
-laplacian operator. To be concise, operator  conserves the two main qualitative properties of operator
conserves the two main qualitative properties of operator  :
:
() is a strictly increasing homeomorphism from
is a strictly increasing homeomorphism from  onto
onto  , such that
, such that  ;
;
() .
.
As consequence, after this work authors considered the  -laplacian equation
-laplacian equation

with  an operator that satisfies the above mentioned properties.
an operator that satisfies the above mentioned properties.
After this paper, the method of lower and upper solutions has been applied to  -laplacian problems with Mixed boundary conditions in [51] and for Neumann and periodic boundary conditions in [52].
-laplacian problems with Mixed boundary conditions in [51] and for Neumann and periodic boundary conditions in [52].
In this case, the definition of a lower and an upper solution, for  being a Carathéodory function, is the direct translation to this case for
being a Carathéodory function, is the direct translation to this case for  the identity.
the identity.
Definition 3.1.
A function  is said to be a lower solution for (3.2) if
is said to be a lower solution for (3.2) if  and
and

A function  is an upper solution for (3.2) if
is an upper solution for (3.2) if  and
and

We will say that  is a solution of (3.2) if it is both a lower and an upper solution.
is a solution of (3.2) if it is both a lower and an upper solution.
Of course, some additional assumptions are needed depending on the considered boundary conditions, that is, we assume (1.3) and (1.5) for the Dirichlet case, (1.7) and (1.8) for the Neumann case, or (1.10) for the periodic case.
The definition of a Nagumo condition, see [52], is the direct adaptation of the one used by Adje in [46]. Note that such condition does not depend on the boundary data of the problem.
Definition 3.2.
One says that the function  satisfies a Nagumo condition with respect to continuous functions
satisfies a Nagumo condition with respect to continuous functions  and
and  , with
, with  , if there exist
, if there exist  , and a continuous function
, and a continuous function  , such that
, such that

where  .
.
Furthermore

where

If  , we replace
, we replace  .
.
It is obvious that, to construct an operator whose fixed points coincide with the solutions of the considered problem, there is no possibility of constructing a Green's function, so no operator analogous to (2.1) can be given. In this case, one can see [52] that the solutions of (3.2) coupled with Dirichlet boundary conditions are the fixed points of the operator  , defined as
, defined as

where  is the unique solution of the equation
is the unique solution of the equation

In the previous mentioned papers, the existence of solutions lying between a pair of well-ordered lower and upper solutions was shown. In [37], the existence of extremal solutions for the Dirichlet problem is proved. As we have noted earlier, in that paper, a new definition of lower and upper solutions with corners is used that allows one to construct a sequence of upper solutions over the function minimum of the solutions in  .
.
Two point nonlinear boundary value conditions have been treated in [53]. In this case  and
and  have been studied. The monotonicity assumptions on
have been studied. The monotonicity assumptions on  and
and  cover the periodic conditions. The proof follows from a truncated problem on
cover the periodic conditions. The proof follows from a truncated problem on  as in the nonlinear part of (1.19) and a truncated boundary conditions as in (2.11).
as in the nonlinear part of (1.19) and a truncated boundary conditions as in (2.11).
Lepin et al. study in [54] the more general equation  together with the two point nonlinear boundary conditions
together with the two point nonlinear boundary conditions

The existence results are on the basis of the monotone properties of functions  and
and  .
.
Functional boundary conditions allow us to consider dependence on some intermediate points of the interval of definition. This is the case of the multipoint boundary conditions:

where  ,
,  , and
, and  ,
,  have the same sign for all
have the same sign for all  and
and  .
.
Many other type of boundary conditions can be treated, is the case, for instance, of the following:

In this situation, it is necessary to consider functions that are not only defined at the extremes of the interval, but also in its interior. Such kind of problems have been treated in [55]. There the authors consider nonlinear functional boundary conditions of the form

with  and
and  a continuous functions that satisfy certain monotonicity conditions which include, as particular cases, the periodic ones.
a continuous functions that satisfy certain monotonicity conditions which include, as particular cases, the periodic ones.
More precisely, it is considered the equation

with  and
and  locally bounded (possibly discontinuous) function and
locally bounded (possibly discontinuous) function and  measurable.
measurable.
The discontinuity on  can be eliminated by the use of the transformation
can be eliminated by the use of the transformation  , where
, where  is given by
is given by

In this case, the studied problem is translated to the usual  -laplacian
-laplacian

and the existence of extremal solutions lying between a pair of well-ordered lower and upper solutions is obtained. The results follows from an appropriate truncated problem and the extension to this case of the arguments used in [37] to get the extremal solutions.
4. General Functional Equations
In this last section, we mention some kind of problems that model different real phenomena that, as we will see, can be presented under the same formulation.
()We consider the classical self-adjoint equation

with  such that
such that  .
.
We can formulate the previous equation in the form

with

()We refer to the usual diffusion equation

with  such that
such that  and
and  .
.
By defining

it is possible to rewrite this equation as

()We study a higher-order differential equation, for instance, the following third-order problem:

By means of the change of variables

we arrive at the following equivalent second-order Dirichlet functional equation:

()Consider the following third-order problem:

Using the same change of variable as above, we arrive at the following second-order differential equation with functional boundary conditions:

In order to include under the same formulation all the previous problems, the following equation is considered in [56]:

coupled with the nonlinear functional boundary conditions (3.13).
The definitions of the lower and upper solutions cover all the usual cases but the Nagumo condition does not generalize the case of  depending only on the first derivative given in Definition 3.2. This gap has been covered in the definition given in [57], where (4.12) is considered coupled with the boundary conditions
depending only on the first derivative given in Definition 3.2. This gap has been covered in the definition given in [57], where (4.12) is considered coupled with the boundary conditions

covering in this case the Sturm-Liouville and the multipoint boundary conditions as particular cases.
5. Final Remarks
It is important to note that in some of the previous results some kind of discontinuities on the spatial variable are assumed. In this case, some techniques developed by Heikkilä and Lakshmikantham in [58] are used.
There is large bibliography on papers related with lower and upper solutions with nonlinear boundary value conditions for first- and higher-order equations.
Problems with impulses, difference equations, and partial differential equations have been studied under this point of view for an important number of researchers.
Some theories as the Thompson's notion of compatibility [59] or the Frigon's tube-solutions [60] give some generalizations of the concept of lower and upper solutions that ensure the existence of solutions of nonlinear boundary problems under weaker assumptions.
References
Picard E: Mémoire sur la théorie des équations aux derivés partielles et las méthode des approximations succesives. Journal de Mathématiques Pures et Appliquées 1890, 6: 145–210.
Picard E: Sur l'application des métodes d'approximations succesives à l'étude de certains équations différentielles ordinaires. Journal de Mathématiques Pures et Appliquées 1893, 9: 217–271.
Perron O: Ein neuer existenzbeweis für die integrale der differentialgleichung
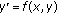 . Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218
. Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218Müller M: Über das fundamentaltheorem in der theorie der gewöhnlichen differentialgleichungen. Mathematische Zeitschrift 1927, 26(1):619–645. 10.1007/BF01475477
Dragoni GS: II problema dei valori ai limiti studiato in grande per le equazioni differenziali del secondo ordine. Mathematische Annalen 1931, 105(1):133–143. 10.1007/BF01455811
Bernfeld SR, Lakshmikantham V: An Introduction to Nonlinear Boundary Value Problems, Mathematics in Science and Engineering, Vol. 10. Academic Press, New York, NY, USA; 1974:xi+386.
Ladde GS, Lakshmikantham V, Vatsala AS: Monotone Iterative Techniques for Nonlinear Differential Equations. Pitman, Boston, Mass, USA; 1985.
Mawhin J: Bounded solutions of nonlinear ordinary differential equations. In Non-Linear Analysis and Boundary Value Problems for Ordinary Differential Equations (Udine), CISM Courses and Lectures. Volume 371. Springer, Vienna, Austria; 1996:121–147.
Mawhin J: Boundary value problems for nonlinear ordinary differential equations: from successive approximations to topology. In Development of Mathematics 1900–1950 (Luxembourg, 1992). Birkhäuser, Basel, Switzerland; 1994:443–477.
Mawhin J: Twenty years of ordinary differential equations through twelve Oberwolfach meetings. Results in Mathematics 1992, 21(1–2):165–189.
Mawhin J: Points fixes, points critiques et problèmes aux limites, Séminaire de Mathématiques Supérieures. Volume 92. Presses de l'Université de Montréal, Montreal, Canada; 1985:162.
De Coster C, Habets P: Two-Point Boundary Value Problems: Lower and Upper Solutions, Mathematics in Science and Engineering. Volume 205. Elsevier, Amsterdam, The Netherlands; 2006:xii+489.
De Coster C, Habets P: The lower and upper solutions method for boundary value problems. In Handbook of Differential Equations. Elsevier/North-Holland, Amsterdam, The Netherlands; 2004:69–160.
De Coster C, Habets P: An overview of the method of lower and upper solutions for ODEs. In Nonlinear Analysis and Its Applications to Differential Equations, Progr. Nonlinear Differential Equations Appl.. Volume 43. Birkhäuser, Boston, Mass, USA; 2001:3–22.
Nagumo M: Uber die differentialgleichung .
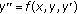 Proceedings of the Physico-Mathematical Society of Japan 1937, 19: 861–866.
Proceedings of the Physico-Mathematical Society of Japan 1937, 19: 861–866.Nagumo M: On principally linear elliptic differential equations of the second order. Osaka Journal of Mathematics 1954, 6: 207–229.
Habets P, Pouso RL: Examples of the nonexistence of a solution in the presence of upper and lower solutions. The ANZIAM Journal 2003, 44(4):591–594. 10.1017/S1446181100012955
Kiguradze IT: A priori estimates for the derivatives of bounded functions satisfying second-order differential inequalities. Differentsial'nye Uravneniya 1967, 3: 1043–1052.
Schrader KW: Solutions of second order ordinary differential equations. Journal of Differential Equations 1968, 4: 510–518. 10.1016/0022-0396(68)90002-8
Tonelli L: Sull'equazione differenziale .
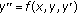 Annali della Scuola Normale Superiore di Pisa 1939, 8(1):75–88.
Annali della Scuola Normale Superiore di Pisa 1939, 8(1):75–88.Epheser H: Über die Existenz der Lösungen von Randwertaufgaben mit gewöhnlichen, nichtlinearen Differentialgleichungen zweiter Ordnung. Mathematische Zeitschrift 1955, 61: 435–454.
Krasnoselskii M: On some boundary value problems. Izvestiya Academy of Sciences USSR 1956, 20: 241–252.
Kiguradze IT: Some Singular Boundary Value Problems for Ordinary Differential Equations. Izdat. Tbilis. Univ., Tbilisi, Russia; 1975.
Kiguradze IT: Some singular boundary value problems for second order nonlinear ordinary differential equations. Differentsial'nye Uravneniya 1968, 4: 1753–1773.
Mawhin J: The Bernstein-Nagumo problem and two-point boundary value problems for ordinary differential equations. In Qualitative Theory of Differential Equations, Vol. I, II (Szeged, 1979), Colloq. Math. Soc. János Bolyai. Volume 30. North-Holland, Amsterdam, The Netherlands; 1981:709–740.
Fabry C, Habets P: Upper and lower solutions for second-order boundary value problems with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(10):985–1007. 10.1016/0362-546X(86)90084-2
Gao WJ, Wang JY: On a nonlinear second order periodic boundary value problem with Carathéodory functions. Annales Polonici Mathematici 1995, 62(3):283–291.
Wang MX, Cabada A, Nieto JJ: Monotone method for nonlinear second order periodic boundary value problems with Carathéodory functions. Annales Polonici Mathematici 1993, 58(3):221–235.
Scorza Dragoni S: Elementi uniti di transformazioni funzionali e problemi di valori ai limiti Rend. Sem. Mat. Univ. Roma 1938, 2(4):255–275.
Ponomarev VD: The existence of the solution of the simplest boundary value problem for a second-order differential equation. Latviĭskiĭ Matematicheskiĭ Ezhegodnik 1978, (22):69–74.
Lepin AYa: Existence of solutions of boundary value problems for a second-order equation. Differential Equations 1990, 26(10):1279–1286.
Lepin LA: On the concepts of lower and upper functions. Differential Equations 1980, 16(10):1750–1759.
Lepin LA: Generalized lower and upper functions and their properties. Latviĭskiĭ Matematicheskiĭ Ezhegodnik 1980, (24):113–123.
Lepin LA: Generalized solutions and the solvability of boundary value problems for a second-order differential equation. Differential Equations 1982, 18(8):1323–1330.
Lepin AYa, Lepin LA, Ponomarev VD: Generalized solvability of nonlinear boundary value problems. Differential Equations 1986, 22(2):198–203.
Lepin AJa, Sadyrbaev FZh: The upper and lower functions method for second order systems. Zeitschrift für Analysis und ihre Anwendungen 2001, 20(3):739–753.
Cherpion M, De Coster C, Habets P: Monotone iterative methods for boundary value problems. Differential and Integral Equations 1999, 12(3):309–338.
Cid JÁ: On extremal fixed points in Schauder's theorem with applications to differential equations. Bulletin of the Belgian Mathematical Society. Simon Stevin 2004, 11(1):15–20.
Kelley JL: General Topology, Graduate Texts in Mathematics, No. 27. Springer, Berlin, Germany; 1975:xiv+298.
Bebernes JW, Fraker R: A priori bounds for boundary sets. Proceedings of the American Mathematical Society 1971, 29: 313–318. 10.1090/S0002-9939-1971-0277807-9
Erbe LH: Existence of solutions to boundary value problems for second order differential equations. Nonlinear Analysis: Theory, Methods & Applications 1982, 6(11):1155–1162. 10.1016/0362-546X(82)90027-X
Virzhbitskiĭ YaV, Sadyrbaev FZh: A two-point boundary value problem for a second-order ordinary differential equation. Latviĭskiĭ Matematicheskiĭ Ezhegodnik 1986, (30):39–42.
Rachůnková I: Upper and lower solutions and multiplicity results. Journal of Mathematical Analysis and Applications 2000, 246(2):446–464. 10.1006/jmaa.2000.6798
Sadyrbaev FZh: Level surfaces of Lyapunov functions and solvability of a two-point boundary value problem. Latviĭskiĭ Matematicheskiĭ Ezhegodnik 1980, (24):172–177.
Sadyrbaev FŽ: A two-point boundary value problem for a system of first-order ordinary differential equations. Latviĭskiĭ Matematicheskiĭ Ezhegodnik 1979, (23):131–136.
Assohoun A: Sur et sous-solutions généralisées et problèmes aux limites du second ordre. Bulletin de la Société Mathématique de Belgique. Série B 1990, 42(3):347–368.
Franco D, O'Regan D: Existence of solutions to second order problems with nonlinear boundary conditions. Discrete and Continuous Dynamical Systems. Series A 2003, (supplement):273–280.
Esteban JR, Vázquez JL: On the equation of turbulent filtration in one-dimensional porous media. Nonlinear Analysis: Theory, Methods & Applications 1986, 10(11):1303–1325. 10.1016/0362-546X(86)90068-4
Herrero MA, Vázquez JL: On the propagation properties of a nonlinear degenerate parabolic equation. Communications in Partial Differential Equations 1982, 7(12):1381–1402. 10.1080/03605308208820255
De Coster C: Pairs of positive solutions for the one-dimensional
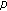 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1994, 23(5):669–681. 10.1016/0362-546X(94)90245-3
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1994, 23(5):669–681. 10.1016/0362-546X(94)90245-3Wang J, Gao W: Existence of solutions to boundary value problems for a nonlinear second order equation with weak Carathéodory functions. Differential Equations and Dynamical Systems 1997, 5(2):175–185.
Cabada A, Pouso RL: Existence result for the problem
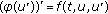 with periodic and Neumann boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(3):1733–1742. 10.1016/S0362-546X(97)00249-6
with periodic and Neumann boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(3):1733–1742. 10.1016/S0362-546X(97)00249-6Cabada A, Pouso RL: Existence results for the problem
 with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1
with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1Lepin AJa, Lepin LA, Sadyrbaev FZh: Two-point boundary value problems with monotonically boundary conditions for one-dimensional φ -Laplacian equations. Functional Differential Equations 2005, 12(3–4):347–363.
Cabada A, Pouso RL: Extremal solutions of strongly nonlinear discontinuous second-order equations with nonlinear functional boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2000, 42(8):1377–1396. 10.1016/S0362-546X(99)00158-3
Cabada A, Pouso RL: Existence theory for functional
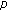 -Laplacian equations with variable exponents. Nonlinear Analysis: Theory, Methods & Applications 2003, 52(2):557–572. 10.1016/S0362-546X(02)00122-0
-Laplacian equations with variable exponents. Nonlinear Analysis: Theory, Methods & Applications 2003, 52(2):557–572. 10.1016/S0362-546X(02)00122-0Cabada A, O'Regan D, Pouso RL: Second order problems with functional conditions including Sturm-Liouville and multipoint conditions. Mathematische Nachrichten 2008, 281(9):1254–1263. 10.1002/mana.200510675
Heikkilä S, Lakshmikantham V: Monotone Iterative Techniques for Discontinuous Nonlinear Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 181. Marcel Dekker, New York, NY, USA; 1994:xii+514.
Thompson HB, Tisdell CC: Nonlinear multipoint boundary value problems for weakly coupled systems. Bulletin of the Australian Mathematical Society 1999, 60(1):45–54. 10.1017/S0004972700033311
Frigon M, Montoki E: Systems of differential inclusions with maximal monotone terms. Journal of Mathematical Analysis and Applications 2006, 323(2):1134–1151. 10.1016/j.jmaa.2005.11.023
Acknowledgments
The author is grateful for professors Jean Mawhin and Felix Ž. Sadyrbaev, their interesting comments have been of great importance in the development of this work. He is also grateful for the anonymous referees whose useful remarks have made the paper more readable. This paper was partially supported by Ministerio de Educación y Ciencia, Spain, Project MTM2007-61724.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cabada, A. An Overview of the Lower and Upper Solutions Method with Nonlinear Boundary Value Conditions. Bound Value Probl 2011, 893753 (2011). https://doi.org/10.1155/2011/893753
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/893753
 -Laplacian Problems and Functional Boundary Conditions
-Laplacian Problems and Functional Boundary Conditions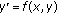 . Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218
. Mathematische Annalen 1915, 76(4):471–484. 10.1007/BF01458218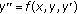 Proceedings of the Physico-Mathematical Society of Japan 1937, 19: 861–866.
Proceedings of the Physico-Mathematical Society of Japan 1937, 19: 861–866.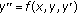 Annali della Scuola Normale Superiore di Pisa 1939, 8(1):75–88.
Annali della Scuola Normale Superiore di Pisa 1939, 8(1):75–88. -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1994, 23(5):669–681. 10.1016/0362-546X(94)90245-3
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 1994, 23(5):669–681. 10.1016/0362-546X(94)90245-3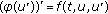 with periodic and Neumann boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(3):1733–1742. 10.1016/S0362-546X(97)00249-6
with periodic and Neumann boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(3):1733–1742. 10.1016/S0362-546X(97)00249-6 with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1
with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1 -Laplacian equations with variable exponents. Nonlinear Analysis: Theory, Methods & Applications 2003, 52(2):557–572. 10.1016/S0362-546X(02)00122-0
-Laplacian equations with variable exponents. Nonlinear Analysis: Theory, Methods & Applications 2003, 52(2):557–572. 10.1016/S0362-546X(02)00122-0