- Research Article
- Open access
- Published:
Approximation of Solutions for Second-Order 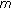 -Point Nonlocal Boundary Value Problems via the Method of Generalized Quasilinearization
-Point Nonlocal Boundary Value Problems via the Method of Generalized Quasilinearization
Boundary Value Problems volume 2011, Article number: 929061 (2011)
Abstract
We discuss the existence and uniqueness of the solutions of a second-order  -point nonlocal boundary value problem by applying a generalized quasilinearization technique. A monotone sequence of solutions converging uniformly and quadratically to a unique solution of the problem is presented.
-point nonlocal boundary value problem by applying a generalized quasilinearization technique. A monotone sequence of solutions converging uniformly and quadratically to a unique solution of the problem is presented.
1. Introduction
The monotone iterative technique coupled with the method of upper and lower solutions [1–7] manifests itself as an effective and flexible mechanism that offers theoretical as well as constructive existence results in a closed set, generated by the lower and upper solutions. In general, the convergence of the sequence of approximate solutions given by the monotone iterative technique is at most linear [8, 9]. To obtain a sequence of approximate solutions converging quadratically, we use the method of quasilinearization [10]. This method has been developed for a variety of problems [11–20]. In view of its diverse applications, this approach is quite an elegant and easier for application algorithms.
The subject of multipoint nonlocal boundary conditions, initiated by Bicadze and Samarskiĭ [21], has been addressed by many authors, for instance, [22–32]. The multipoint boundary conditions appear in certain problems of thermodynamics, elasticity and wave propagation, see [23] and the references therein. The multipoint boundary conditions may be understood in the sense that the controllers at the endpoints dissipate or add energy according to censors located at intermediate positions.
In this paper, we develop the method of generalized quasilinearization to obtain a sequence of approximate solutions converging monotonically and quadratically to a unique solution of the following second-order  point nonlocal boundary value problem
point nonlocal boundary value problem


where  is continuous and
is continuous and  are nonnegative real constants such that
are nonnegative real constants such that  ,
,  and
and  with
with 
Here we remark that [26] studies (1.1) with the boundary conditions of the form

A perturbed integral equation equivalent to the problem (1.1) and (1.3) considered in [26] is

where

It can readily be verified that the solution given by (1.4) does not satisfy (1.1). On the other hand, by Green's function method, a unique solution of the problem (1.1) and (1.3) is

where  is given by (1.5). Thus, (1.6) represents the correct form of the solution for the problem (1.1) and (1.3).
is given by (1.5). Thus, (1.6) represents the correct form of the solution for the problem (1.1) and (1.3).
2. Preliminaries
For  we define
we define  where
where  It can easily be verified that the homogeneous problem associated with (1.1)-(1.2) has only the trivial solution. Therefore, by Green's function method, the solution of (1.1)-(1.2) can be written as
It can easily be verified that the homogeneous problem associated with (1.1)-(1.2) has only the trivial solution. Therefore, by Green's function method, the solution of (1.1)-(1.2) can be written as

where  is the Green's function and is given by
is the Green's function and is given by

Note that  on
on 
We say that  is a lower solution of the boundary value problem (1.1) and (1.2) if
is a lower solution of the boundary value problem (1.1) and (1.2) if

and  is an upper solution of (1.1) and (1.2) if
is an upper solution of (1.1) and (1.2) if

Definition 2.1.
A continuous function  is called a Nagumo function if
is called a Nagumo function if

for  . We say that
. We say that  satisfies a Nagumo condition on
satisfies a Nagumo condition on  relative to
relative to  if for every
if for every  and
and  there exists a Nagumo function
there exists a Nagumo function  such that
such that 
We need the following result [33] to establish the main result.
Theorem 2.2.
Let  be a continuous function satisfying the Nagumo condition on
be a continuous function satisfying the Nagumo condition on  where
where  are continuous functions such that
are continuous functions such that  for all
for all  Then there exists a constant
Then there exists a constant  (depending only on
(depending only on  the Nagumo function
the Nagumo function  ) such that every solution
) such that every solution  of (1.1)-(1.2) with
of (1.1)-(1.2) with  ,
,  satisfies
satisfies 
If  are assumed to be lower and upper solutions of (1.1)-(1.2), respectively, in the statement of Theorem 2.2, then there exists a solution,
are assumed to be lower and upper solutions of (1.1)-(1.2), respectively, in the statement of Theorem 2.2, then there exists a solution,  of (1.1) and (1.2) such that
of (1.1) and (1.2) such that  ,
, 
Theorem 2.3.
Assume that  are, respectively, lower and upper solutions of (1.1)-(1.2). If
are, respectively, lower and upper solutions of (1.1)-(1.2). If  is decreasing in
is decreasing in  for each
for each  then
then  on
on 
Proof.
Let us define  so that
so that  and satisfies the boundary conditions
and satisfies the boundary conditions

For the sake of contradiction, let  have a positive maximum at some
have a positive maximum at some  . If
. If  , then
, then  and
and  On the other hand, in view of the decreasing property of
On the other hand, in view of the decreasing property of  in
in  we have
we have

which is a contradiction. If we suppose that  has a positive maximum at
has a positive maximum at  , then it follows from the first of boundary conditions (2.6) that
, then it follows from the first of boundary conditions (2.6) that

which implies that  Now as
Now as  ,
,  ,
,  ,
,  therefore we obtain a contradiction. We have a similar contradiction at
therefore we obtain a contradiction. We have a similar contradiction at  Thus, we conclude that
Thus, we conclude that  ,
, 
3. Main Results
Theorem 3.1.
Assume that
the functions  are, respectively, lower and upper solutions of (1.1)-(1.2) such that
are, respectively, lower and upper solutions of (1.1)-(1.2) such that  on
on 
the function  satisfies a Nagumo condition relative to
satisfies a Nagumo condition relative to  and
and  on
on  where
where  is a positive constant depending on
is a positive constant depending on  and the Nagumo function
and the Nagumo function  . Further, there exists a function
. Further, there exists a function  such that
such that  with
with  on
on  where
where

Then, there exists a monotone sequence  of approximate solutions converging uniformly to a unique solution of the problems (1.1)-(1.2).
of approximate solutions converging uniformly to a unique solution of the problems (1.1)-(1.2).
Proof.
For  we define
we define  and consider the following modified
and consider the following modified  -point BVP
-point BVP

We note that  are, respectively, lower and upper solutions of (3.2) and for every
are, respectively, lower and upper solutions of (3.2) and for every  we have
we have

where  As
As

so  is a Nagumo function. Furthermore, there exists a constant
is a Nagumo function. Furthermore, there exists a constant  depending on
depending on  , and Nagumo function
, and Nagumo function  such that
such that

where  . Thus, any solution
. Thus, any solution  of (3.2) with
of (3.2) with  ,
,  satisfies
satisfies  on
on  and hence it is a solution of (1.1)-(1.2).
and hence it is a solution of (1.1)-(1.2).
Let us define a function  by
by

In view of the assumption  it follows that
it follows that  and satisfies
and satisfies  on
on  Therefore, by Taylor's theorem, we obtain
Therefore, by Taylor's theorem, we obtain

We set

and observe that

By the mean value theorem, we can find  and
and  (
( depend on
depend on  , resp.), such that
, resp.), such that

Letting

we note that

Let us define  as
as

Clearly  is continuous and bounded on
is continuous and bounded on  and satisfies a Nagumo condition relative to
and satisfies a Nagumo condition relative to  . For every
. For every  and
and  , we consider the
, we consider the  -point BVP
-point BVP

Using (3.9), (3.12) and (3.13), we have

Thus,  are lower and upper solutions of (3.14), respectively. Since
are lower and upper solutions of (3.14), respectively. Since  satisfies a Nagumo condition, there exists a constant
satisfies a Nagumo condition, there exists a constant  (depending on
(depending on  and a Nagumo function) such that any solution
and a Nagumo function) such that any solution  of (3.14) with
of (3.14) with  satisfies
satisfies  on
on 
Now, we choose  and consider the problem
and consider the problem

Using  , (3.9), (3.12) and (3.13), we obtain
, (3.9), (3.12) and (3.13), we obtain

which imply that  and
and  are lower and upper solutions of (3.16). Hence by Theorems 2.2 and 2.3, there exists a unique solution
are lower and upper solutions of (3.16). Hence by Theorems 2.2 and 2.3, there exists a unique solution  of (3.16) such that
of (3.16) such that

Note that the uniqueness of the solution follows by Theorem 2.3. Using (3.9) and (3.13) together with the fact that  is solution of (3.16), we find that
is solution of (3.16), we find that  is a lower solution of (3.2), that is,
is a lower solution of (3.2), that is,

In a similar manner, it can be shown by using  , (3.12), (3.13), and (3.19) that
, (3.12), (3.13), and (3.19) that  and
and  are lower and upper solutions of the following
are lower and upper solutions of the following  -point BVP
-point BVP

Again, by Theorems 2.2 and 2.3, there exists a unique solution  of (3.20) such that
of (3.20) such that

Continuing this process successively, we obtain a bounded monotone sequence  of solutions satisfying
of solutions satisfying

where  is a solution of the problem
is a solution of the problem

and is given by

Since  is bounded on
is bounded on  ,
,  ,
,  therefore it follows that the sequences
therefore it follows that the sequences  are uniformly bounded and equicontinuous on
are uniformly bounded and equicontinuous on  Hence, by Ascoli-Arzela theorem, there exist the subsequences and a function
Hence, by Ascoli-Arzela theorem, there exist the subsequences and a function  such that
such that  uniformly on
uniformly on  as
as  Taking the limit
Taking the limit  we find that
we find that  which consequently yields
which consequently yields

This proves that  is a solution of (3.2).
is a solution of (3.2).
Theorem 3.2.
Assume that  and
and  hold. Further, one assumes that
hold. Further, one assumes that
the function  satisfies
satisfies  for
for  where
where  and
and 
Then, the convergence of the sequence  of approximate solutions (obtained in Theorem 3.1) is quadratic.
of approximate solutions (obtained in Theorem 3.1) is quadratic.
Proof.
Let us set  so that
so that  satisfies the boundary conditions
satisfies the boundary conditions

In view of the assumption  for every
for every  it follows that
it follows that

Now, by Taylor's theorem, we have

where  ,
,  ,
,  ,
,  on
on  ,
,  and
and  ,
,  with
with  satisfying
satisfying  on
on  Also, in view of (3.13), we have
Also, in view of (3.13), we have

where  and
and  ,
, 
Now we show that  By the mean value theorem, for every
By the mean value theorem, for every  and
and  we obtain
we obtain

Let  for some
for some  Then
Then  and (3.30) becomes
and (3.30) becomes

In particular, taking  and using (3.27), we have
and using (3.27), we have

which contradicts that  Similarly, letting
Similarly, letting  for some
for some  we get a contradiction. Thus, it follows that
we get a contradiction. Thus, it follows that  for every
for every  , which implies that
, which implies that  and consequently, (3.28) and (3.29) take the form
and consequently, (3.28) and (3.29) take the form

where  and
and

Now, by a comparison principle, we can obtain  on
on  , where
, where  is a solution of the problem
is a solution of the problem

Since  is continuous and bounded on
is continuous and bounded on  , there exist
, there exist  (independent of
(independent of  ) such that
) such that  on
on  Since
Since  on
on  so we can rewrite (3.35) as
so we can rewrite (3.35) as

whose solution is given by

where

Introducing the integrating factor  such that
such that  (3.34) takes the form
(3.34) takes the form

Integrating (3.39) from  to
to  and using
and using  we obtain
we obtain

which can alternatively be written as

where  ,
,  . Using the fact that
. Using the fact that  together with (3.41) yields
together with (3.41) yields

which, on substitutingin (3.37), yields

where

Taking the maximum over  and then solving (3.43) for
and then solving (3.43) for  we obtain
we obtain

Also, it follows from (3.33) that

Integrating (3.46) from  to
to  and using
and using  (from the boundary condition
(from the boundary condition  we obtain
we obtain

which, in view of the fact  and (3.45), yields
and (3.45), yields

where

As  , there exists
, there exists  such that
such that

Integrating (3.46) from  to
to  (
( ) and using (3.50), we have
) and using (3.50), we have

Using (3.45) in (3.34), we obtain

where  . Since
. Since  is bounded on
is bounded on  ,
,  we can choose
we can choose  such that
such that  on
on  ,
,  and
and  so that (3.52) takes the form
so that (3.52) takes the form

Integrating (3.53) from  to
to  (
( ), and using (3.51), we find that
), and using (3.51), we find that

Letting

it follows from (3.51) and (3.54) that

Hence, from (3.48) and (3.56), it follows that

where  From (3.45) and (3.57) with
From (3.45) and (3.57) with

we obtain

This proves the quadratic convergence in  norm.
norm.
Example 3.3.
Consider the boundary value problem

Let  and
and  be, respectively, lower and upper solutions of (3.60). Clearly
be, respectively, lower and upper solutions of (3.60). Clearly  and
and  are not the solutions of (3.60) and
are not the solutions of (3.60) and  Also, the assumptions of Theorem 3.1 are satisfied. Thus, the conclusion of Theorem 3.1 applies to the problem (3.60).
Also, the assumptions of Theorem 3.1 are satisfied. Thus, the conclusion of Theorem 3.1 applies to the problem (3.60).
References
Ladde GS, Lakshmikantham V, Vatsala AS: Monotone Iterative Techniques for Nonlinear Differential Equations, Monographs, Advanced Texts and Surveys in Pure and Applied Mathematics, 27. Pitman, Boston, Mass, USA; 1985:x+236.
Nieto JJ, Jiang Y, Jurang Y: Monotone iterative method for functional-differential equations. Nonlinear Analysis: Theory, Methods & Applications 1998, 32(6):741–747. 10.1016/S0362-546X(97)00524-5
Vatsala AS, Yang J: Monotone iterative technique for semilinear elliptic systems. Boundary Value Problems 2005, 2005(2):93–106. 10.1155/BVP.2005.93
Drici Z, McRae FA, Devi JV: Monotone iterative technique for periodic boundary value problems with causal operators. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(6):1271–1277. 10.1016/j.na.2005.06.033
Jiang D, Nieto JJ, Zuo W: On monotone method for first and second order periodic boundary value problems and periodic solutions of functional differential equations. Journal of Mathematical Analysis and Applications 2004, 289(2):691–699. 10.1016/j.jmaa.2003.09.020
Nieto JJ, Rodríguez-López R: Monotone method for first-order functional differential equations. Computers & Mathematics with Applications 2006, 52(3–4):471–484. 10.1016/j.camwa.2006.01.012
Ahmad B, Sivasundaram S: The monotone iterative technique for impulsive hybrid set valued integro-differential equations. Nonlinear Analysis: Theory, Methods & Applications 2006, 65(12):2260–2276. 10.1016/j.na.2006.01.033
Cabada A, Nieto JJ: Rapid convergence of the iterative technique for first order initial value problems. Applied Mathematics and Computation 1997, 87(2–3):217–226. 10.1016/S0096-3003(96)00285-8
Lakshmikantham V, Nieto JJ: Generalized quasilinearization for nonlinear first order ordinary differential equations. Nonlinear Times and Digest 1995, 2(1):1–9.
Bellman RE, Kalaba RE: Quasilinearization and Nonlinear Boundary-Value Problems, Modern Analytic and Computional Methods in Science and Mathematics. Volume 3. American Elsevier, New York, NY, USA; 1965:ix+206.
Lakshmikantham V, Vatsala AS: Generalized Quasilinearization for Nonlinear Problems, Mathematics and Its Applications. Volume 440. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1998:x+276.
Cabada A, Nieto JJ: Quasilinearization and rate of convergence for higher-order nonlinear periodic boundary-value problems. Journal of Optimization Theory and Applications 2001, 108(1):97–107. 10.1023/A:1026413921997
Ahmad B, Nieto JJ, Shahzad N: The Bellman-Kalaba-Lakshmikantham quasilinearization method for Neumann problems. Journal of Mathematical Analysis and Applications 2001, 257(2):356–363. 10.1006/jmaa.2000.7352
Eloe PW, Gao Y: The method of quasilinearization and a three-point boundary value problem. Journal of the Korean Mathematical Society 2002, 39(2):319–330.
Akyildiz FT, Vajravelu K: Existence, uniqueness, and quasilinearization results for nonlinear differential equations arising in viscoelastic fluid flow. Differential Equations & Nonlinear Mechanics 2006, 2006:-9.
Ahmad B: A quasilinearization method for a class of integro-differential equations with mixed nonlinearities. Nonlinear Analysis: Real World Applications 2006, 7(5):997–1004. 10.1016/j.nonrwa.2005.09.003
Krivec R, Mandelzweig VB: Quasilinearization method and WKB. Computer Physics Communications 2006, 174(2):119–126. 10.1016/j.cpc.2004.12.017
Amster P, De Nápoli P: A quasilinearization method for elliptic problems with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(10):2255–2263. 10.1016/j.na.2006.03.016
Ahmad B, Alsaedi A, Alghamdi BS: Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions. Nonlinear Analysis: Real World Applications 2008, 9(4):1727–1740. 10.1016/j.nonrwa.2007.05.005
Ahmad B, Nieto JJ: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(10):3291–3298. 10.1016/j.na.2007.09.018
Bicadze AV, Samarskiĭ AA: Some elementary generalizations of linear elliptic boundary value problems. Doklady Akademii Nauk SSSR 1969, 185: 739–740.
Gupta CP: A second order
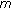 -point boundary value problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 1995, 24(10):1483–1489. 10.1016/0362-546X(94)00204-U
-point boundary value problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 1995, 24(10):1483–1489. 10.1016/0362-546X(94)00204-UMa R: Multiple positive solutions for nonlinear
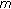 -point boundary value problems. Applied Mathematics and Computation 2004, 148(1):249–262. 10.1016/S0096-3003(02)00843-3
-point boundary value problems. Applied Mathematics and Computation 2004, 148(1):249–262. 10.1016/S0096-3003(02)00843-3Eloe PW, Ahmad B: Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009Webb JRL, Infante G: Positive solutions of nonlocal boundary value problems: a unified approach. Journal of the London Mathematical Society 2006, 74(3):673–693. 10.1112/S0024610706023179
Khan RA: Generalized approximations and rapid convergence of solutions of
 -point boundary value problems. Applied Mathematics and Computation 2007, 188(2):1878–1890. 10.1016/j.amc.2006.11.138
-point boundary value problems. Applied Mathematics and Computation 2007, 188(2):1878–1890. 10.1016/j.amc.2006.11.138Pei M, Chang SK: The generalized quasilinearization method for second-order three-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2779–2790. 10.1016/j.na.2007.02.025
Pei M, Chang SK: A quasilinearization method for second-order four-point boundary value problems. Applied Mathematics and Computation 2008, 202(1):54–66. 10.1016/j.amc.2008.01.026
Ahmad B: Approximation of solutions of the forced Duffing equation with
 -point boundary conditions. Communications in Applied Analysis 2009, 13(1):11–20.
-point boundary conditions. Communications in Applied Analysis 2009, 13(1):11–20.Wang L, Pei M, Ge W: Existence and approximation of solutions for nonlinear second-order four-point boundary value problems. Mathematical and Computer Modelling 2009, 50(9–10):1348–1359. 10.1016/j.mcm.2008.11.018
Chang Y-K, Nieto JJ, Li W-S: On impulsive hyperbolic differential inclusions with nonlocal initial conditions. Journal of Optimization Theory and Applications 2009, 140(3):431–442. 10.1007/s10957-008-9468-1
Graef JR, Webb JRL: Third order boundary value problems with nonlocal boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(5–6):1542–1551. 10.1016/j.na.2008.12.047
Grossinho M, Minhós FM: Upper and lower solutions for higher order boundary value problems. Nonlinear Studies 2005, 12(2):165–176.
Acknowledgment
The author is grateful to the referees and professor G. Infante for their valuable suggestions and comments that led to the improvement of the original paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alsaedi, A. Approximation of Solutions for Second-Order 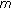 -Point Nonlocal Boundary Value Problems via the Method of Generalized Quasilinearization.
Bound Value Probl 2011, 929061 (2011). https://doi.org/10.1155/2011/929061
-Point Nonlocal Boundary Value Problems via the Method of Generalized Quasilinearization.
Bound Value Probl 2011, 929061 (2011). https://doi.org/10.1155/2011/929061
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/929061
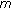 -point boundary value problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 1995, 24(10):1483–1489. 10.1016/0362-546X(94)00204-U
-point boundary value problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 1995, 24(10):1483–1489. 10.1016/0362-546X(94)00204-U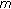 -point boundary value problems. Applied Mathematics and Computation 2004, 148(1):249–262. 10.1016/S0096-3003(02)00843-3
-point boundary value problems. Applied Mathematics and Computation 2004, 148(1):249–262. 10.1016/S0096-3003(02)00843-3 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521–527. 10.1016/j.aml.2004.05.009 -point boundary value problems. Applied Mathematics and Computation 2007, 188(2):1878–1890. 10.1016/j.amc.2006.11.138
-point boundary value problems. Applied Mathematics and Computation 2007, 188(2):1878–1890. 10.1016/j.amc.2006.11.138 -point boundary conditions. Communications in Applied Analysis 2009, 13(1):11–20.
-point boundary conditions. Communications in Applied Analysis 2009, 13(1):11–20.