- Research Article
- Open access
- Published:
Uniqueness of solutions for fourth-order nonlocal boundary value problems
Boundary Value Problems volume 2006, Article number: 23875 (2006)
Abstract
Uniqueness implies uniqueness relationships are examined among solutions of the fourth-order ordinary differential equation, , satisfying
, satisfying -point,
-point, -point, and
-point, and -point nonlocal boundary conditions.
-point nonlocal boundary conditions.
References
Agarwal RP: Compactness condition for boundary value problems. Equadiff (Brno) 1997, 9: 1-23.
Clark S, Henderson J: Uniqueness implies existence and uniqueness criterion for nonlocal boundary value problems for third order differential equations. to appear in Proceedings of the American Mathematical Society
Conti M, Terracini S, Verzini G: Infinitely many solutions to fourth order superlinear periodic problems. Transactions of the American Mathematical Society 2004,356(8):3283-3300. 10.1090/S0002-9947-03-03514-1
Ehme J, Hankerson D: Existence of solutions for right focal boundary value problems. Nonlinear Analysis 1992,18(2):191-197. 10.1016/0362-546X(92)90093-T
Franco D, O'Regan D, Perán J: Fourth-order problems with nonlinear boundary conditions. Journal of Computational and Applied Mathematics 2005,174(2):315-327. 10.1016/j.cam.2004.04.013
Graef JR, Qian C, Yang B: A three point boundary value problem for nonlinear fourth order differential equations. Journal of Mathematical Analysis and Applications 2003,287(1):217-233. 10.1016/S0022-247X(03)00545-6
Gupta CP: A Dirichlet type multi-point boundary value problem for second order ordinary differential equations. Nonlinear Analysis 1996,26(5):925-931. 10.1016/0362-546X(94)00338-X
Gupta CP, Ntouyas SK, Tsamatos PCh:Solvability of an
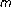 -point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036
-point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036Hartman P:Unrestricted
 -parameter families. Rendiconti del Circolo Matematico di Palermo. Serie II 1958, 7: 123-142. 10.1007/BF02854523
-parameter families. Rendiconti del Circolo Matematico di Palermo. Serie II 1958, 7: 123-142. 10.1007/BF02854523Hartman P:On
 -parameter families and interpolation problems for nonlinear ordinary differential equations. Transactions of the American Mathematical Society 1971, 154: 201-226.
-parameter families and interpolation problems for nonlinear ordinary differential equations. Transactions of the American Mathematical Society 1971, 154: 201-226.Henderson J: Uniqueness of solutions of right focal point boundary value problems for ordinary differential equations. Journal of Differential Equations 1981,41(2):218-227. 10.1016/0022-0396(81)90058-9
Henderson J: Existence of solutions of right focal point boundary value problems for ordinary differential equations. Nonlinear Analysis 1981,5(9):989-1002. 10.1016/0362-546X(81)90058-4
Henderson J:Right
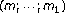 boundary value problems for third order differential equations. Journal of Mathematical and Physical Sciences 1984,18(4):405-413.
boundary value problems for third order differential equations. Journal of Mathematical and Physical Sciences 1984,18(4):405-413.Henderson J:Existence theorems for boundary value problems for
 th-order nonlinear difference equations. SIAM Journal on Mathematical Analysis 1989,20(2):468-478. 10.1137/0520032
th-order nonlinear difference equations. SIAM Journal on Mathematical Analysis 1989,20(2):468-478. 10.1137/0520032Henderson J: Uniqueness implies existence for three-point boundary value problems for second order differential equations. Applied Mathematics Letters 2005,18(8):905-909. 10.1016/j.aml.2004.07.032
Henderson J, Karna B, Tisdell CC: Existence of solutions for three-point boundary value problems for second order equations. Proceedings of the American Mathematical Society 2005,133(5):1365-1369. 10.1090/S0002-9939-04-07647-6
Henderson J, McGwier RW Jr.: Uniqueness, existence, and optimality for fourth-order Lipschitz equations. Journal of Differential Equations 1987,67(3):414-440. 10.1016/0022-0396(87)90135-5
Henderson J, Yin WKC: Existence of solutions for fourth order boundary value problems on a time scale. Journal of Difference Equations and Applications 2003,9(1):15-28.
Ill'in VA, Moiseev EI: Nonlocal boundary value problem of the second kind for a Sturm-Liouville operator. Differential Equations 1987,23(8):979-987.
Jackson LK: Uniqueness of solutions of boundary value problems for ordinary differential equations. SIAM Journal on Applied Mathematics 1973,24(4):535-538. 10.1137/0124054
Jackson LK: Existence and uniqueness of solutions of boundary value problems for third order differential equations. Journal of Differential Equations 1973,13(3):432-437. 10.1016/0022-0396(73)90002-8
Jackson LK: Boundary value problems for Lipschitz equations. In Differential Equations. Edited by: Ahmed S, Keener M, Lazer A. Academic Press, New York; 1980:31-50.
Karna B: Extremal points for the fourth order boundary value problems. Mathematical Sciences Research Journal 2003,7(10):382-393.
Klaasen GA:Existence theorems for boundary value problems for
 th order ordinary differential equations. The Rocky Mountain Journal of Mathematics 1973, 3: 457-472. 10.1216/RMJ-1973-3-3-457
th order ordinary differential equations. The Rocky Mountain Journal of Mathematics 1973, 3: 457-472. 10.1216/RMJ-1973-3-3-457Kong L, Kong Q:Positive solutions of nonlinear
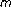 -point boundary value problems on a measure chain. Journal of Difference Equations and Applications 2003,9(6):615-627. 10.1080/1023619031000060963
-point boundary value problems on a measure chain. Journal of Difference Equations and Applications 2003,9(6):615-627. 10.1080/1023619031000060963Lasota A, Łuczyński M: A note on the uniqueness of two point boundary value problems I. Zeszyty Naukowe Uniwersytetu Jagiellonskiego, Prace Matematyczne 1968, 12: 27-29.
Lasota A, Opial Z: On the existence and uniqueness of solutions of a boundary value problem for an ordinary second-order differential equation. Colloquium Mathematicum 1967, 18: 1-5.
Liu Y, Ge W: Existence theorems of positive solutions for fourth-order four point boundary value problems. Analysis and Applications (Singapore) 2004,2(1):71-85.
Lü H, Yu H, Liu Y: Positive solutions for singular boundary value problems of a coupled system of differential equations. Journal of Mathematical Analysis and Applications 2005,302(1):14-29. 10.1016/j.jmaa.2004.08.003
Ma R: Positive solutions for second-order three-point boundary value problems. Applied Mathematics Letters 2001,14(1):1-5. 10.1016/S0893-9659(00)00102-6
Ma R:Existence of positive solutions for superlinear semipositone
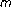 -point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391
-point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391Ma R, Castaneda N:Existence of solutions of nonlinear
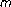 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320Ma R: Multiple positive solutions for a semipositone fourth-order boundary value problem. Hiroshima Mathematical Journal 2003,33(2):217-227.
Ma R: Some multiplicity results for an elastic beam equation at resonance. Applied Mathematics and Mechanics 1993,14(2):193-200. 10.1007/BF02453362
Ma JJ, Zhang FR: Solvability of a class of fourth-order two-point boundary value problems. Heilongjiang Daxue Ziran Kexue Xuebao 2001,18(2):19-22.
Marchant TR: Higher-order interaction of solitary waves on shallow water. Studies in Applied Mathematics 2002,109(1):1-17. 10.1111/1467-9590.00001
Palamides PK:Multi point boundary-value problems at resonance for
 -order differential equations: positive and monotone solutions. Electronic Journal of Differential Equations 2004,2004(25):1-14.
-order differential equations: positive and monotone solutions. Electronic Journal of Differential Equations 2004,2004(25):1-14.Pei MH, Chang SK: Existence and uniqueness theorems of solutions for a class fourth-order boundary value problems. Kyungpook Mathematical Journal 2001,41(2):299-309.
Peterson AC: Focal Green's functions for fourth-order differential equations. Journal of Mathematical Analysis and Applications 1980,75(2):602-610. 10.1016/0022-247X(80)90104-3
Peterson DE: Uniqueness, existence, and comparison theorems for ordinary differential equations, Doctoral dissertation. , Nebraska; 1973.
Spanier EH: Algebraic Topology. McGraw-Hill, New York; 1966:xiv+528.
Vidossich G: On the continuous dependence of solutions of boundary value problems for ordinary differential equations. Journal of Differential Equations 1989,82(1):1-14. 10.1016/0022-0396(89)90164-2
Webb JRL: Positive solutions of some three point boundary value problems via fixed point index theory. Nonlinear Analysis 2001,47(7):4319-4332. 10.1016/S0362-546X(01)00547-8
Zhang Z, Wang J: Positive solutions to a second order three-point boundary value problem. Journal of Mathematical Analysis and Applications 2003,285(1):237-249. 10.1016/S0022-247X(03)00396-2
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Henderson, J., Ma, D. Uniqueness of solutions for fourth-order nonlocal boundary value problems. Bound Value Probl 2006, 23875 (2006). https://doi.org/10.1155/BVP/2006/23875
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/23875
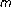 -point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036
-point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036 -parameter families. Rendiconti del Circolo Matematico di Palermo. Serie II 1958, 7: 123-142. 10.1007/BF02854523
-parameter families. Rendiconti del Circolo Matematico di Palermo. Serie II 1958, 7: 123-142. 10.1007/BF02854523 -parameter families and interpolation problems for nonlinear ordinary differential equations. Transactions of the American Mathematical Society 1971, 154: 201-226.
-parameter families and interpolation problems for nonlinear ordinary differential equations. Transactions of the American Mathematical Society 1971, 154: 201-226.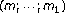 boundary value problems for third order differential equations. Journal of Mathematical and Physical Sciences 1984,18(4):405-413.
boundary value problems for third order differential equations. Journal of Mathematical and Physical Sciences 1984,18(4):405-413. th-order nonlinear difference equations. SIAM Journal on Mathematical Analysis 1989,20(2):468-478. 10.1137/0520032
th-order nonlinear difference equations. SIAM Journal on Mathematical Analysis 1989,20(2):468-478. 10.1137/0520032 th order ordinary differential equations. The Rocky Mountain Journal of Mathematics 1973, 3: 457-472. 10.1216/RMJ-1973-3-3-457
th order ordinary differential equations. The Rocky Mountain Journal of Mathematics 1973, 3: 457-472. 10.1216/RMJ-1973-3-3-457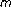 -point boundary value problems on a measure chain. Journal of Difference Equations and Applications 2003,9(6):615-627. 10.1080/1023619031000060963
-point boundary value problems on a measure chain. Journal of Difference Equations and Applications 2003,9(6):615-627. 10.1080/1023619031000060963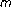 -point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391
-point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391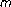 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320 -order differential equations: positive and monotone solutions. Electronic Journal of Differential Equations 2004,2004(25):1-14.
-order differential equations: positive and monotone solutions. Electronic Journal of Differential Equations 2004,2004(25):1-14.