- Research Article
- Open access
- Published:
Parabolic inequalities with nonstandard growths and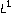 data
data
Boundary Value Problems volume 2006, Article number: 29286 (2006)
Abstract
We prove an existence result for solutions of nonlinear parabolic inequalities with data in Orlicz spaces.
data in Orlicz spaces.
References
Adams RA: Sobolev Spaces, Pure and Applied Mathematics. Volume 65. Academic Press, New York; 1975:xviii+268.
Donaldson T: Inhomogeneous Orlicz-Sobolev spaces and nonlinear parabolic initial value problems. Journal of Differential Equations 1974,16(2):201-256. 10.1016/0022-0396(74)90012-6
Elmahi A, Meskine D: Parabolic equations in Orlicz spaces. Journal of the London Mathematical Society. Second Series 2005,72(2):410-428. 10.1112/S0024610705006630
Elmahi A, Meskine D:Strongly nonlinear parabolic equations with natural growth terms and
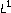 data in Orlicz spaces. Portugaliae Mathematica. Nova Série 2005,62(2):143-183.
data in Orlicz spaces. Portugaliae Mathematica. Nova Série 2005,62(2):143-183.Elmahi A, Meskine D: Strongly nonlinear parabolic equations with natural growth terms in Orlicz spaces. Nonlinear Analysis. Theory, Methods & Applications 2005,60(1):1-35.
Gossez J-P: Nonlinear elliptic boundary value problems for equations with rapidly (or slowly) increasing coefficients. Transactions of the American Mathematical Society 1974, 190: 163-205.
Gossez J-P: Some approximation properties in Orlicz-Sobolev spaces. Studia Mathematica 1982,74(1):17-24.
Gossez J-P: A strongly nonlinear elliptic problem in Orlicz-Sobolev spaces. In Nonlinear Functional Analysis and Its Applications, Part 1 (Berkeley, Calif, 1983), Proc. Sympos. Pure Math.. Volume 45. American Mathematical Society, Rhode Island; 1986:455-462.
Gossez J-P, Mustonen V: Variational inequalities in Orlicz-Sobolev spaces. Nonlinear Analysis. Theory, Methods & Applications 1987,11(3):379-392. 10.1016/0362-546X(87)90053-8
Le VK, Schmitt K: Quasilinear elliptic equations and inequalities with rapidly growing coefficients. Journal of the London Mathematical Society. Second Series 2000,62(3):852-872. 10.1112/S0024610700001423
Robert J: Inéquations variationnelles paraboliques fortement non linéaires. Journal de Mathématiques Pures et Appliquées. Neuvième Série 1974, 53: 299-320.
Rudd M: Nonlinear constrained evolution in Banach spaces, M.S. thesis. University of Utah, Utah; 2003.
Rudd M: Weak and strong solvability of parabolic variational inequalities in Banach spaces. Journal of Evolution Equations 2004,4(4):497-517. 10.1007/s00028-004-0153-z
Rudd M, Schmitt K: Variational inequalities of elliptic and parabolic type. Taiwanese Journal of Mathematics 2002,6(3):287-322.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aboulaich, R., Achchab, B., Meskine, D. et al. Parabolic inequalities with nonstandard growths and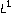 data.
Bound Value Probl 2006, 29286 (2006). https://doi.org/10.1155/BVP/2006/29286
data.
Bound Value Probl 2006, 29286 (2006). https://doi.org/10.1155/BVP/2006/29286
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/29286
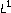 data in Orlicz spaces. Portugaliae Mathematica. Nova Série 2005,62(2):143-183.
data in Orlicz spaces. Portugaliae Mathematica. Nova Série 2005,62(2):143-183.