- Research Article
- Open access
- Published:
Existence and multiplicity of weak solutions for a class of degenerate nonlinear elliptic equations
Boundary Value Problems volume 2006, Article number: 41295 (2006)
Abstract
The goal of this paper is to study the existence and the multiplicity of non-trivial weak solutions for some degenerate nonlinear elliptic equations on the whole space . The solutions will be obtained in a subspace of the Sobolev space
. The solutions will be obtained in a subspace of the Sobolev space . The proofs rely essentially on the Mountain Pass theorem and on Ekeland's Variational principle.
. The proofs rely essentially on the Mountain Pass theorem and on Ekeland's Variational principle.
References
Alves CO, Gonçalves JV, Miyagaki OH:On elliptic equations in
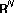 with critical exponents. Electronic Journal of Differential Equations 1996,1996(9):1-11.
with critical exponents. Electronic Journal of Differential Equations 1996,1996(9):1-11.Ambrosetti A, Rabinowitz PH: Dual variational methods in critical point theory and applications. Journal of Functional Analysis 1973,14(4):349-381. 10.1016/0022-1236(73)90051-7
Brezis H: Analyse Fonctionnelle. Théorie et Applications, Collection of Applied Mathematics for the Master's Degree. Masson, Paris; 1983.
De Nápoli P, Mariani MC:Mountain pass solutions to equations of
 -Laplacian type. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2003,54(7):1205-1219.
-Laplacian type. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2003,54(7):1205-1219.Díaz JI: Nonlinear Partial Differential Equations and Free Boundaries. Vol. I. Elliptic Equations, Research Notes in Mathematics. Volume 106. Pitman, Massachusetts; 1985.
do Ó JMB: Existence of solutions for quasilinear elliptic equations. Journal of Mathematical Analysis and Applications 1997,207(1):104-126. 10.1006/jmaa.1997.5270
do Ó JMB:Solutions to perturbed eigenvalue problems of the
 -Laplacian in
-Laplacian in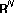 . Electronic Journal of Differential Equations 1997,1997(11):1-15.
. Electronic Journal of Differential Equations 1997,1997(11):1-15.Ekeland I: On the variational principle. Journal of Mathematical Analysis and Applications 1974,47(2):324-353. 10.1016/0022-247X(74)90025-0
Gonçalves JV, Miyagaki OH:Multiple positive solutions for semilinear elliptic equations in
 involving subcritical exponents. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1998,32(1):41-51.
involving subcritical exponents. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1998,32(1):41-51.Mihăilescu M, Rădulescu V: Ground state solutions of non-linear singular Schrödinger equations with lack of compactness. Mathematical Methods in the Applied Sciences 2003,26(11):897-906. 10.1002/mma.403
Motreanu D, Rădulescu V: Eigenvalue problems for degenerate nonlinear elliptic equations in anisotropic media. Boundary Value Problems 2005,2005(2):107-127. 10.1155/BVP.2005.107
Pflüger K:Existence and multiplicity of solutions to a
 -Laplacian equation with nonlinear boundary condition. Electronic Journal of Differential Equations 1998,1998(10):1-13.
-Laplacian equation with nonlinear boundary condition. Electronic Journal of Differential Equations 1998,1998(10):1-13.Rabinowitz PH: On a class of nonlinear Schrödinger equations. Zeitschrift für Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathématiques et de Physique Appliquées 1992,43(2):270-291.
Rădulescu V, Smets D: Critical singular problems on infinite cones. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2003,54(6):1153-1164.
Şt. Cîrstea F, Rădulescu V: Multiple solutions of degenerate perturbed elliptic problems involving a subcritical Sobolev exponent. Topological Methods in Nonlinear Analysis 2000,15(2):283-300.
Tarantello G: On nonhomogeneous elliptic equations involving critical Sobolev exponent. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1992,9(3):281-304.
Willem M: Analyse harmonique réelle, Methods Collection. Hermann, Paris; 1995.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mihăilescu, M. Existence and multiplicity of weak solutions for a class of degenerate nonlinear elliptic equations. Bound Value Probl 2006, 41295 (2006). https://doi.org/10.1155/BVP/2006/41295
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/41295
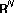 with critical exponents. Electronic Journal of Differential Equations 1996,1996(9):1-11.
with critical exponents. Electronic Journal of Differential Equations 1996,1996(9):1-11. -Laplacian type. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2003,54(7):1205-1219.
-Laplacian type. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2003,54(7):1205-1219. -Laplacian in
-Laplacian in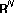 . Electronic Journal of Differential Equations 1997,1997(11):1-15.
. Electronic Journal of Differential Equations 1997,1997(11):1-15. involving subcritical exponents. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1998,32(1):41-51.
involving subcritical exponents. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1998,32(1):41-51. -Laplacian equation with nonlinear boundary condition. Electronic Journal of Differential Equations 1998,1998(10):1-13.
-Laplacian equation with nonlinear boundary condition. Electronic Journal of Differential Equations 1998,1998(10):1-13.