- Research
- Open access
- Published:
Study of the asymptotic eigenvalue distribution and trace formula of a second order operator-differential equation
Boundary Value Problems volume 2011, Article number: 7 (2011)
Abstract
The purpose of writing this article is to show some spectral properties of the Bessel operator equation, with spectral parameter-dependent boundary condition. This problem arises upon separation of variables in heat or wave equations, when one of the boundary conditions contains partial derivative with respect to time. To illustrate the problem and the proof in detail, as a first step, the corresponding operator's discreteness of the spectrum is proved. Then, the nature of the eigenvalue distribution is established. Finally, based on these results, a regularized trace formula for the eigenvalues is obtained.
MSC: 34B05; 34G20; 34L20; 34L05; 47A05; 47A10.
Introduction
Let L2 = L2 (H, [0, 1]) ⊕ H, where H is a separable Hilbert space with a scalar product (·, ·) and a norm ||·|| inside of it. By definition, a scalar product in L2 is

where Y = {y (t), y1}, Z = {z (t), z1} and y(t), z(t) ∈ L2 (H, [0, 1]) for which L2 (H, [0, 1]) is a space of vector functions y(t) such that  .
.
Now, consider the equation:


in L2 (H, [0, 1]), where A is a self-adjoint positive-definite operator in H which has a compact inverse operator. Further, suppose the operator-valued function q(t) is weakly measurable, and ||q(t)|| is bounded on [0, 1] with the following properties:
-
1.
q(t) has a second-order weak derivative on [0, 1], and q(l)(t) (l = 0, 1, 2) are self-adjoint operators in H for each t ∈ [0, 1], [q(l)(t)]* = q(l)(t), q(l)(t) ∈ σ1(H). Here σ1(H) is a trace class, i.e., a class of compact operators in separable Hilbert space H, whose singular values form a convergent series (denoting the compact operator by B, then its singular values are the eigenvalues of
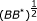 ). If {φ
n
} is a basis formed by the orthonormal eigenvectors of B, then
). If {φ
n
} is a basis formed by the orthonormal eigenvectors of B, then 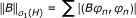 . For simplicity, denote the norm in σ1(H) by ||·||1.
. For simplicity, denote the norm in σ1(H) by ||·||1. -
2.
The functions ||q(l)(t)||1 (l = 0, 1, 2) are bounded on [0, 1].
-
3.
The relation
 is true for each f ∈ H.
is true for each f ∈ H.
State that if q(t) ≡ 0, a self-adjoint operator denoted by L0 can be associated with problem (2), (3) whose definition will be given later.
If q(t) ≢ 0, the operators L and Q are defined by L = L0 + Q, and Q : Q {y (t), y1} = {q(t) y(t), 0} which is a bounded self-adjoint operator in L2.
After the above definitions and the assumptions, the asymptotic of the eigenvalue distribution and regularized trace of the considered problem will be studied. It is clear that because of the appearance of an eigenvalue parameter in the boundary condition at the end point, the operator associated with problem (2), (3) in L2 (H, [0, 1]) is not self-adjoint. Introduce a new Hilbert space L2 (H, [0, 1]) ⊕ H with the scalar product defined by formula (1) similar to one used in [1]. Then, in this space, the operator becomes self-adjoint.
In [2], Walter considers a scalar Sturm-Liouville problem with an eigenvalue parameter λ in the boundary conditions. He shows that one can associate a self-adjoint operator with that by finding a suitable Hilbert space. Further, he obtains the expansion theorem by reference to the self-adjointness of that operator. His approach was used by Fulton in [3] later on.
As for the differential operator equations, to the best of this author's knowledge in the articles [1, 4–6], an eigenvalue parameter appears in the boundary conditions. In [4], the following problem is considered:

where A = A* > E, and u(x) ∈ L2 (H, (0, b)). It is proved that the operator associated with this problem has a discrete spectrum, iff : A has a discrete spectrum. The eigenvalues of this problem form two sequences like  and
and  where n, k ∈ N, and μ
k
is an eigenvalue of A. This is obtained from appearance of λ in the boundary condition.
where n, k ∈ N, and μ
k
is an eigenvalue of A. This is obtained from appearance of λ in the boundary condition.
In [5], both boundary conditions depend on λ. It is shown that the operator defined in the space L2 (H, (0, 1)) ⊕ H ⊕ H is symmetric positive-definite. Further, the asymptotic formulas for eigenvalues are obtained.
In this author's previous study [6], for the operator considered in [4], the trace formula has been established.
If h = 0 in (3), then the boundary condition takes the form y(1) = 0. This problem is considered in [[7], Theorem 2.2], where the trace formula is established. It is proved that there exists a subsequence of natural numbers {n
m
} such that  , where μ
n
and λ
n
are the eigenvalues of perturbed and non-perturbed operators. For definition of {n
m
}, see also [[8], Lemma 1].
, where μ
n
and λ
n
are the eigenvalues of perturbed and non-perturbed operators. For definition of {n
m
}, see also [[8], Lemma 1].
For a scalar case, please refer to [9], where the following problem

is considered on the interval [0, π]. Then, the sum  is calculated.
is calculated.
In comparison with the above mentioned articles, here we consider a differential operator equation which has a singularity at 0, and the boundary condition at 1 involves both the eigenvalue parameter λ and physical parameter h < 0.
Problems with λ-dependent boundary conditions arise upon separation of variables in the heat and wave equations. We can also refer to [10–17], where boundary-value problems for ordinary differential operators with eigenvalue-dependent boundary conditions are studied.
In 1953, Gelfand and Levitan [18] considered the Sturm-Liouville operator

and derived the formula  , where μ
n
are the eigenvalues of the above operator. For q (x) ≡ 0 the eigenvalues of the operator are given by λ
n
= n2.
, where μ
n
are the eigenvalues of the above operator. For q (x) ≡ 0 the eigenvalues of the operator are given by λ
n
= n2.
It is worthwhile to note that, several studies are devoted to searching a regularized trace for the concrete operators (e.g., [9–18]), as well as differential-operator equations (e.g., [6–8, 19]) and discrete abstract operators (e.g., [20–22]). For further detailed discussion of the subject, please refer to [23].
Trace formulas are used for the approximation of the first eigenvalues of the operators [24, 25] to solve inverse problems [26, 27]. They are also applied to index theory of linear operators [28, 29].
To summarize this study, in Section 1, it is proved that the operator associated with (2), (3) is self-adjoint and has a discrete spectrum. In Section 2, we establish an asymptotic formula for the eigenvalues. To do this, the zeros of the characteristic equation (Lemmas 2.1, 2.2, 2.3) are searched in detail. In Section 3, by using the asymptotic for the eigenvalues, we prove that the series called "a regularized trace" converges absolutely (Lemma 3.1). This enables us to arrange the terms of the series in a suitable way for calculation as in (3.9). To calculate the sum of this series, we introduce a function whose poles are zeros of the characteristic equation, the residues at poles of which are the terms of our series. Finally, we establish a trace formula by integrating this function along the expanded contours.
In conclusion, we apply the results of our study to a boundary value problem generated by a partial differential equation.
1 Definition of L0and proof of discreteness of the spectrum
Let  , where
, where  is a set of vector functions with values in H (see [30], p. 57) that vanish in the vicinity of zero and are infinitely differentiable in the norm of H. Also, on
is a set of vector functions with values in H (see [30], p. 57) that vanish in the vicinity of zero and are infinitely differentiable in the norm of H. Also, on  define the operator
define the operator  :
:

Using integration by parts it is easy to see that  is symmetric. Denote its closure by L0 and show that it is self-adjoint. To do that, consider the adjoint operator of
is symmetric. Denote its closure by L0 and show that it is self-adjoint. To do that, consider the adjoint operator of  as
as  . By definition, vector
. By definition, vector  if for each
if for each  it holds
it holds

and Z* = {z* (t), z*} ∈ L2. However, using integration by parts from (1.1), it is obvious that  with
with  and l[z] ∈ L2 (H, [0, 1])}. In other words, z(t) has a first-order derivative on [0, 1] which is absolutely continuous in the norm of H and z (0) = z'(0) = 0, Az(t) ∈ L2 (H, [0, 1]) and
and l[z] ∈ L2 (H, [0, 1])}. In other words, z(t) has a first-order derivative on [0, 1] which is absolutely continuous in the norm of H and z (0) = z'(0) = 0, Az(t) ∈ L2 (H, [0, 1]) and  .
.
Now, the vector  if and only if for any
if and only if for any  (1.1) holds, Z* ∈ L2 and
(1.1) holds, Z* ∈ L2 and  .
.
By virtue of  ,
,  , we can state that any vector Z from
, we can state that any vector Z from  must also belong to
must also belong to  and
and  . On the other hand, it could be verified that relation (1.1) is also true for
. On the other hand, it could be verified that relation (1.1) is also true for

Therefore,  . In other words,
. In other words,  is a self-adjoint operator. However, we know that
is a self-adjoint operator. However, we know that  . Thus, the closure of
. Thus, the closure of  is a self-adjoint operator
is a self-adjoint operator  , which we will denote by L0.
, which we will denote by L0.
By virtue of all as stated above, L0 is defined as

By the properties of ν ≥ 1, A > E, it follows that L0 is a positive-definite operator. To show that, for each Y ∈ D (L0), we have

Since the embedding  is continuous ([[31], Theorem 1.7.7], [[32], p. 48]), then,
is continuous ([[31], Theorem 1.7.7], [[32], p. 48]), then,  , where c > 0 is a constant.
, where c > 0 is a constant.
Thus,

which shows that L0 is a positive-definite operator.
To prove the discreteness of the spectrum, we will use the following Rellich's theorem (see [[33], p. 386]).
Theorem 1.1. Let B be a self-adjoint operator in H satisfying (Bφ, φ) ≥ (φ, φ), φ ∈ D B , where D B is a domain of B.
Then, the spectrum of B is discrete if and only if the set of all vectors φ ∈ D B , satisfying (Bφ, φ) ≤ 1 is precompact.
Let γ1 ≤ γ2 ≤ · · · ≤ γ n ≤ · · · be the eigenvalues of A counted with multiplicity and φ1, φ2,..., φ n ,... be the corresponding orthonormal eigenvectors in H.
Take y k (t) = (y (t), φ k ). Then

Hence, using the Rellich's theorem, we come to the following theorem:
Theorem 1.2. If the operator A-1 is compact in H, then the operator L0 has a discrete spectrum.
Proof. By virtue of positive-definiteness of L0, by Rellich's theorem, it is sufficient to show that the set of vectors

is precompact in L2.
To prove this theorem, consider the following lemma.
Lemma 1.1. For any given ε > 0, there is a number R = R(ε), such that

Proof. From (1.1) for Y ∈ Y :

Since γ
R
→ ∞ for R → ∞, for any given ε > 0, we could choose R(ε) such that  . Therefore, for this choice of R the inequality
. Therefore, for this choice of R the inequality

holds. On the other hand, by virtue of (1.3):

From (1.4) and the above, it follows that

This proves Lemma 1.1.
Now, turn to the proof of Theorem 1.2. Assume, Y ∈ Y. Denote the set of all vector-functions  , by E
R
. Then, from Lemma 1.1 it follows that for the set Y, E
R
is an ε-net in L2. Therefore, to prove the precompactness of the set Y, we must prove the precompactness of E
R
in L2. Since |y
k
(1)| ≤ 1 (k = 1,..., R), it is sufficient to show that y
k
(t) (k = 1,..., R) satisfies the criteria of precompactness in L2 (0, 1) [[34], p. 291]. In other words, y
k
(t), (k = 1,..., R) must be equicontinuous and bounded with respect to the norm in L2 (0, 1). To show that, using (1.3) results in
, by E
R
. Then, from Lemma 1.1 it follows that for the set Y, E
R
is an ε-net in L2. Therefore, to prove the precompactness of the set Y, we must prove the precompactness of E
R
in L2. Since |y
k
(1)| ≤ 1 (k = 1,..., R), it is sufficient to show that y
k
(t) (k = 1,..., R) satisfies the criteria of precompactness in L2 (0, 1) [[34], p. 291]. In other words, y
k
(t), (k = 1,..., R) must be equicontinuous and bounded with respect to the norm in L2 (0, 1). To show that, using (1.3) results in

which proves the boundedness of the functions y k (t) (k = 1,..., R). Assume that y k (t) is a zero outside the interval (0, 1). Then, by using the following relation

we have



From the above, for |η| < ε we have

This shows the equicontinuity of E R , and it completes the proof of the discreteness of the spectrum of L0.
2 The derivation of the asymptotic formula for eigenvalue distribution of L0
Suppose that the eigenvalues of A are γ n ~ anα (n → ∞, a > 0, α > 0). Then, by virtue of the spectral expansion of the self-adjoint operator A, we get the following boundary value problem for the coefficients y k (t) = (y(t), φ k ):


The solution to problem (2.1) from L2 (0, 1) is

For this solution to satisfy (2.2), it is necessary and sufficient to hold

at least for one γ k (λ ≠ γ k ). Therefore, the spectrum of the operator L0 consists of those real values of λ ≠ γ k , such that at least for one k

where  . Then, by using (2.4) and identity
. Then, by using (2.4) and identity  [[35], p. 56], we get
[[35], p. 56], we get

Find the eigenvalues of the operator L0 which are less than γ
k
. These values correspond to the imaginary roots of Equation 2.5. By taking  and using [[35], p. 51]:
and using [[35], p. 51]:

we get

or equivalently

Now, consider the quadratic equation  whose roots are given as
whose roots are given as

Therefore, the coefficients for yn in (2.6) become positive for

Further, let N be the number of positive roots of the function in (2.6), and W be the number of sign changes in its coefficients. Because the radius of convergence of this series is ∞, then by Descartes' rule of signs [[36], p. 52] W - N is a nonnegative even number. From (2.7), W = 1, therefore N = 1. Hence, beginning with some k, Equation 2.6 has exactly one positive root corresponding to the imaginary root of Equation 2.5.
Now, find the asymptotic of the imaginary roots of Equation 2.5. For z = iy and using the asymptotic of J ν (z) for imaginary z a large |z| [[37], p. 976]

This means (2.4) is equivalent to

from which

Using (2.8) in  , we come up with the asymptotic formula for the eigenvalues of L0 which are less than γ
k
, we come up with the asymptotic formula for the eigenvalues of L0 which are less than γ
k

Now, find the asymptotic of those solutions of Equation 2.3 which are greater than γ k , i.e., the real roots of Equation 2.5. By virtue of the asymptotic for a large |z| [[35], p. 222]

Equation 2.5 becomes

Hence,

where m is a large integer. Therefore, we can state the following Lemma 2.1:
Lemma 2.1. The eigenvalues of the operator L0 form two sequences

where  . Denote the imaginary and real roots of Equation 2.2 by x0,kand xm, k, respectively.
. Denote the imaginary and real roots of Equation 2.2 by x0,kand xm, k, respectively.
State the following two lemmas.
Lemma 2.2. Equation 2.5 has no complex roots except the pure imaginary or real roots.
Proof. λ is real since it is eigenvalue of self-adjoint operator associated with problem (2.1), (2.2). γ k is real by our assumption (A* = A). Hence, the roots of (2.5) are square roots of real numbers. Lemma 2.2 is proved.
Let C be a rectangular contour with vertices at ±iB, ±iB + A
m
, where  , and B is a large positive number. Further, assume that this contour bypasses the origin and the imaginary root at -ix0,kalong the small semicircle on the right side of the imaginary axis and ix0,kon the left.
, and B is a large positive number. Further, assume that this contour bypasses the origin and the imaginary root at -ix0,kalong the small semicircle on the right side of the imaginary axis and ix0,kon the left.
Then, we claim that the following lemma is true.
Lemma 2.3. For a sufficiently large integer m, the number of zeros of the function

inside of C is exactly m.
Proof. Since  is an entire function of z, then the number of its zeros inside of C equals:
is an entire function of z, then the number of its zeros inside of C equals:

In the above, we have used the following identities:

As the integrand is an odd function. the order of its numerator in the vicinity of zero is O(zν+1), and the order of its denominator is O(zν), the integral along the left part of contour vanishes. Now, consider the integrals along the remaining three sides of the contour. On these sides [[35], p. 221, p. 88]

where

η1,ν (z) and η2,ν (z) are of order  for large |z|.
for large |z|.
For simplicity, denote the integrand by f(z), then

One can analogously show that the integral along the lower side tends to the same number.
To calculate the integral along the fourth side, use the relations:  for large |z|, and
for large |z|, and  .
.
Since  is bounded on the right-hand side of the contour, we get
is bounded on the right-hand side of the contour, we get

Consequently, the limit of the integral along the entire contour is  . However, as the integral must be an integer, it should be equal to m. This completes the proof of Lemma 2.3.
. However, as the integral must be an integer, it should be equal to m. This completes the proof of Lemma 2.3.
By using the above results, derive the asymptotic formula for the eigenvalue distribution of L0. To do that, denote the eigenvalue distribution of the operator L0 by N (λ, L0). Then:

where

Since γ
k
~ a · kα, then  . That is
. That is

From Lemmas 2.2 and 2.3 and the asymptotic of xm, k, it follows that one can find a number c such that for a large m

From this inequality, it follows that N2(λ) is less than  , where
, where  is the number of the positive integer pairs (m, k) satisfying the inequality
is the number of the positive integer pairs (m, k) satisfying the inequality

Also, N2(λ) is greater than  , where
, where  is the number of the positive integer pairs for which
is the number of the positive integer pairs for which

To summarize, we have

Thus, by (2.12) and (2.13) as in [[38], Section 3, Lemma 2] we have:

where  .
.
From the above, we have

Therefore, by virtue of (2.11) and (2.15), we have

For α > 2

and consequently,  ,
,  .
.
For α > 2,  or,
or,  .
.
For α = 2, N (λ) ~ (c1 + c2) λ from which λ n (L0) ~ dn, d = (c1 + c2)-1.
Then, as Q is a bounded operator in L2, it follows from the relation for the resolvents of the operators L0 and L [[30], p. 219]

that the spectrum of L is also discrete. By virtue of the last equality and the properties that hold for s numbers of compact operators [[30], pp. 44, 49] as in [[38], Section 3, Lemma 2], for the eigenvalues of L denoted by μ n (L), we have

Therefore, we can state the following theorem:
Theorem 2.1. If γ n ~ anα (0 < a, α > 0), then

where

For simplicity, we will denote the eigenvalues of L0 and L by λ n and μ n , respectively.
3 Regularized trace of the operator L
Now make use of the theorem proved in [20] for abstract operators. At first, introduce the following notations.
Let A0 be a self-adjoint positive discrete operator, {λ
n
} be its eigenvalues arranged in ascending order, {φ
j
} be a basis formed by the eigenvectors of A0, B be a perturbation operator, and {μ
n
} be the eigenvalues of A0 + B. Also, assume that  . For operators A0 and B in [[20], Theorem 1], the following theorem is proved.
. For operators A0 and B in [[20], Theorem 1], the following theorem is proved.
Theorem 3.1. Let the operator B be such that D(A0) ⊂ D(B), and let there exist a number δ ∈ [0, 1) such that  has a bounded extension, and number ω∈ [0, 1), ω + δ < 1 such that
has a bounded extension, and number ω∈ [0, 1), ω + δ < 1 such that  is a trace class operator. Then, there exists a subsequence of natural numbers
is a trace class operator. Then, there exists a subsequence of natural numbers  and a subsequence of contours Γ
m
∈ C, that for ω ≥ δ the formula
and a subsequence of contours Γ
m
∈ C, that for ω ≥ δ the formula

is true.
Note that the conditions of this theorem are satisfied for L0 and L. That is, if we take A0 = L0, B = Q, then  is bounded. For
is bounded. For  and α > 2, from asymptotic (2.16), we will have that
and α > 2, from asymptotic (2.16), we will have that  is a trace class operator. If α < 2, then
is a trace class operator. If α < 2, then  will be a trace class operator for
will be a trace class operator for  .
.
Thus, by the statement of Theorem 3.1, for α > 2, we have

where ψ1(x), ψ2(x),... are the orthonormal eigenvectors of L0.
Introduce the following notation:

and investigate the sum of series  , which as will be seen later, is independent of the choice of
, which as will be seen later, is independent of the choice of  . We will call the sum of this series a regularized trace of the operator L0.
. We will call the sum of this series a regularized trace of the operator L0.
Now, we calculate the norm for the eigen-vectors of the operator L0 in L2. To do this, we will use the following identity obtained from the Bessel equation"

As α → β, we get

We also consider the following identities:

By the above identities and also by the equation

satisfied by xm, k, we obtain

Therefore,

So, the orthonormal eigen-vectors of L0 are

Now, we prove the following lemma.
Lemma 3.1. If the operator function q(t) has properties 1, 2, and also α > 0, then

Proof. Assume that f
k
(t) = (q(t) φ
k
, φ
k
). By Lemma 2.1 we have  .
.
So, in virtue of the inequality  [[35], p. 666] and properties 1 and 2 we have
[[35], p. 666] and properties 1 and 2 we have

To estimate the second series in (3.5), we use the relation  .
.
By hypothesis of Lemma 3.1 α > 0. Therefore, denoting this sum by s, we have

This proves Lemma 3.1.
Now, assume that


for small δ > 0.
Then, we can state the following theorem.
Theorem 3.2. Let the conditions of Theorem 2.1, (3.6) and (3.7) hold. If the operator-value function q(t) has properties 1-3, then the following formula is true

Proof. By virtue of lemma 3.1 we have

At first evaluate the inner sum in the second term on the right hand side of (3.9). To do this, as N → ∞ investigate the asymptotic behavior of the function

To derive a formula for R
N
(t), show for each fixed value of k, the m th term of the sum R
N
(t) as a residue at the point xm, kof some complex variable function with poles at  .
.
For this purpose, consider the following function:

The poles of this function are x0,k,...,xN - 1,kand j1,..., j N (J ν (j n ) = 0). The residue at j n equals

Now, compute the residue at xm, k:

Denote the right hand side of (3.10) by G(z). Since xm, ksatisfies equation (2.4), by setting z = xm, kand using the identity

we have

Therefore,

Consider the contour C mentioned in Lemma 2.3 as the contour of integration. According to Lemmas 2.1 and 2.3, for a sufficiently large N, we have xN - 1,k< A N < xN, kand j N < A N < jN+1.
It could easily be verified that in the vicinity of zero, the function g(z) is of order O (zν). By virtue of this asymptotic and because g(z) is an odd function, the integral along the left-hand side of the contour C vanishes when r (radius of a semicircle) goes to zero.
Furthermore, if z = u + iv, then for large |v| and u ≥ 0, the integrand will be of order O (e|v|(2t- 2)). That is, for a given value of A N , the integrals along the upper and lower sides of C go to zero as B → ∞ (0 < t < 1). Thus, we obtain

where

Also, along the contour C for  ,
,  , we have |tz| → ∞. Therefore, in integral (3.11), we could replace the Bessel functions by their asymptotic at large arguments. Hence, from
, we have |tz| → ∞. Therefore, in integral (3.11), we could replace the Bessel functions by their asymptotic at large arguments. Hence, from

as N → ∞ we have

Denote the right side of (3.12) by J:

Then the limit of (3.11) becomes:

Using (3.6) and (3.13), we obtain

Moreover, if (3.7) holds, then by virtue of the known relation for a large N [[35], p. 642]

Hence, we will have

Using property 2 and the asymptotic of xm, k

Earlier it was obtained that under the assumptions 1-3 (see [[7], Theorem 2.2])

Thus, from (3.14) to (3.18), we have

Consequently,

In a similar way to the one considered above, we get (this time Equation 2.5 has no imaginary roots, so the contour C will only bypass the origin on the right half-plane):

Finally, combining (3.19) and (3.20), we get

which completes the proof.
Remark. It should be noted that in condition 1, property q(l)(t) ∈ σ1,  may be weakened. Namely, we may just require to hold
may be weakened. Namely, we may just require to hold

Then formula (3.8) takes the form  . There exist the bounded functions that are not from the trace class, even compact, but satisfy the above stated condition. Now, introduce an example.
. There exist the bounded functions that are not from the trace class, even compact, but satisfy the above stated condition. Now, introduce an example.
Example. We consider the following boundary value problem:



in the cylinder ∂Ω × [0, 1], where Ω is a circle in R2 ((x, y) ∈ R2) of radius 1. Also, ∂Ω is a circumference of this circle, n is an exterior normal to the surface ∂Ω × [0, 1] and h = const.. Looking for the solution of this problem, which can be represented as u(x, y, z, t) = U(x, y, z)T(t), we have

Thus, the left-hand side of this equality depends only on t, while the right-hand side on x, y, z. This means they are equal to some constant which we will denote by -λ. Therefore,

and (3.22) becomes like

Using the cylindric coordinates x = r cos φ, y = r sin φ, z = z, we have

The boundary condition in (3.24) becomes

We will solve this problem by separation of variables. Taking U(r, φ, z) = V (r, z)ϕ(φ), q(r, φ, z) = Q(r, z), and  , ν = const., we get
, ν = const., we get

By making  substitution, we get
substitution, we get

and (3.25), (3.23) take the form:

where Q(r, z) is a real-valued function which is continuous on [0, 1] × [0, 1], and has second partial derivative with respect to r on [0, 1] for each fixed z. Fourier series of this function and its partial derivatives converge, respectively, to their values. Also assume that

Now, rewrite the problem in the differential operator form:

where v(r) = V1(r, ·) is a vector function with the values from L2(0, 1). Operators A and q(r) are defined in the following way:

Obviously, the operator A is self-adjoint, positive-definite, and A-1 is a compact operator in L2(0, 1). Also, the eigenvalues of A are of the form:

Then, by virtue of Theorem 2.1, the eigenvalues of this problem behave like  .
.
Using the statement of Theorem 3.2, we have

where μ
i
are the eigenvalues of problem (3.28) with q(r) ≡ 0. Now calculate 

In a similar way, we can find

Therefore,

The authors declare that they have no competing interests
References
Gorbachuk VI, Rybak MA: On Boundary Value Problems for Sturm-Liouville Operator Equation with Eigenvalue Dependent Boundary Condition. Direct and Inverse Problems of Scattering Theory Kiev 1981, 3-13.
Walter J: Regular eigenvalue problems with eigenvalue parameter in the boundary conditions. Math Z 1973, 133: 301-312. 10.1007/BF01177870
Fulton ChT: Two-point boundary value problems with eigenvalue parameter contained in the boundary condition. Proc R Soc Edinburgh 1977, 77A: 293-308.
Rybak MA: On asymptotic of eigenvalue distribution of some boundary value problems for Sturm-Liouville operator equation. Ukr Math J 1980, 32(2):248-252.
Aliev BA: Asymptotic behavior of eigenvalue of one boundary value problem for elliptic dif.-operat. equation of second order. Ukr Math J 2006, 58(8):1146-1152.
Aslanova NM: A trace formula of one boundary value problem for the Sturm-Liouville operator equation. Siberian Math J 2008, 49(6):1207-1215.
Hashimov IF: Calculation of regularized trace for Sturm-Liouville operator with singularity on finite segment. M, DEP. VINITI, No 7340-B89 1989, 37.
Maksudov FG, Bayramogly M, Adigezalov AA: On regularized trace of Sturm-Liouville operator on finite segment with unbounded operator coefficient. DAN SSSR 1984, 277(4):795-799.
Sadovnichii VA: On some identities for eigenvalues of singular differential operators. Relations for zeros of Bessel function. Westnik MGU, ser Math Mech 1971, 3: 77-86.
Meleshko SV, Pokorniy YV: On a vibrational boundary-value problem. Differ Equ 1987, 23(8):1466-1467.
Ahn HJ: Vibrations of a pendulum consisting of a bob suspended from a wire. Quart Appl Math 1981, 39(1):109-117.
Racheva MR: Bounds for the principal eigenvalue of nonhomogeneous bar with a tip mass. C.R Acad Bulgare Sci 2001, 54(11):23-26.
Kapustin NY, Moiceev EI: On basicity in L p of a system of eigenfunctions responding to two problems with a spectral parameter in the boundary conditions. Differensialniye uravneniya 2000, 36(10):1357-1360.
Kapustin NY, Moiceev EI: On pecularities of the root space of a spectral problem with a spectral parameter in the boundary condition. Docl RAN 2002, 385(1):20-24.
Kerimov NB, Mirzoev VS: On basis properties of one spectral problem with spectral parameter dependent boundary condition. Siberian Math J 2003, 44(5):1041-1045.
Yakubov S: Solution of irregular problems by the asymptotic method. Asympt Anal 2000, 22: 129-148.
Bayramoglu M, Sahinturk H: Higher order regularized trace formula for the regular Sturm-Liouville equation contained spectral parameter in the boundary condition. Appl Math Comput 2007, 186(2):1591-1599. 10.1016/j.amc.2006.08.066
Gelfand IM, Levitan BM: About one simple identity for eigenvalue of second order differential operator. DAN SSSR 1953, 88(4):593-596.
Aslanova NM: Trace formula for Sturm-Liouville operator equation. Proc Math Mech Natl Acad Sci Azerb 2007, XXVI: 53-61.
Sadovnichii VA, Podolskii VE: Trace of operators with relatively compact perturbation. Matem Sbor 2002, 193(2):129-152.
Dubrovskii VV: Abstract trace formulas for elliptic smooth differential operators given on compact manifolds. Diff Urav 1991, 27(12):2164-2166.
Halberg CJA Jr, Kramer VA: A generalization of the trace concept. Duke Math J 1960, 27(4):607-617. 10.1215/S0012-7094-60-02758-7
Sadovnichii VA, Podolskii VE: Trace of operators. Uspech Math Nauk 2006, 61(5):89-156.
Dikii LA: Trace formulas for Sturm-Liouville differential operators. Uspech Mathem Nauk XIII 1958, 3(81):111-143.
Sadovnichii VA, Podolskii VE: On the class of Sturm-Liouville operators and approximate calculation of first eigenvalues. Mat Sbornik 1998, 189(1):133-148.
Hochstadt H: On the determination of a Hill's equation from its spectrum. Arch Rational Mech Anal 1965, 19(5):353-362.
Levitan BM: Regularized trace and conditions for smooth periodicity for potential of Sturm-Liouville equation. Sib Matem J 1981, 22(2):137-148.
Fedosov BV: About index of elliptic family on manifold with edge. Doklad AN SSSR 1979, 248(5):1066-1069.
Gesztesy F, Simon B: Topological invariance of the Witten index. J Funct Anal 1988, 79(1):91-102. 10.1016/0022-1236(88)90031-6
Gorbachuk VI, Gorbachuk ML: Boundary value problems for differential-operator equations. Nauk Dumka, Kiev 1984, 284. (Russian)
Yakubov S, Yakubov Ya: Differential-Operator Equations Ordinary and Partial Differential Equations. Chapman and Hall/CRC, Boca Raton; 2000:568.
Lions J-L, Magenes E: Nonhomogeneous boundary value problems and their applications. Nauka, Moscow 1971, 371.
Naymark MA: Linear Differential Operators. Nauka, M 1969, 528.
Smirnov WI: Course of Mathematics. Nauka, M 1959, 5: 655.
Watson GN: A Treatise on the Theory of Bessel Function. IL, M 1949, 1: 798.
Polya G, Szego G: Problems and Theorems from Analysis, II part. IL, M 1978, 2: 431.
Gradstein IS, Rijik IM: Tables of Integrals, Sums, Series and Products. Nauka, M 1971, 1108.
Gorbachuk WI, Gorbachuk ML: On some class of boundary value problems for Sturm-Liouville operator with operator potential. Ukr Mathem J 1972, 24(3):291-305.
Acknowledgements
The author would like to express his thanks to Dr. Yaghoob Ebrahimi, U.S.Fulbright Scholar assigned to Khazar University during 2009-10 academic year, for the latter's help in editing, interpretation, and modification of the initial version of this study.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aslanova, N.M. Study of the asymptotic eigenvalue distribution and trace formula of a second order operator-differential equation. Bound Value Probl 2011, 7 (2011). https://doi.org/10.1186/1687-2770-2011-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2011-7
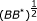 ). If {φ
n
} is a basis formed by the orthonormal eigenvectors of B, then
). If {φ
n
} is a basis formed by the orthonormal eigenvectors of B, then 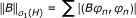 . For simplicity, denote the norm in σ1(H) by ||·||1.
. For simplicity, denote the norm in σ1(H) by ||·||1. is true for each f
is true for each f