Mean-field backward doubly stochastic differential equations and related SPDEs

Abstract

Existence and uniqueness result of the solutions to mean-field backward doubly stochastic differential equations (BDSDEs in short) with locally monotone coefficients as well as the comparison theorem for these equations are established. As a preliminary step, the existence and uniqueness result for the solutions of mean-field BDSDEs with globally monotone coefficients is also established. Furthermore, we give the probabilistic representation of the solutions for a class of stochastic partial differential equations by virtue of mean-field BDSDEs, which can be viewed as the stochastic Feynman-Kac formula for SPDEs of mean-field type.

1 Introduction

In this paper, we study a new kind of stochastic partial differential equations (SPDEs):

$$\begin{array}{rcl}u(t,x)& =& E\left[\mathrm{\Phi }(X_T^{0,x_0},x)\right]+{\int }_t^T\mathcal{L}u(s,x)ds\\ +{\int }_t^{T}E\left[f(s,X_s^{0,x_0},x,u(s,X_s^{0,x_0}),u(s,x),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x))\right]ds\\ +{\int }_t^{T}E\left[g\right(s,X_s^{0,x_0},x,u(s,X_s^{0,x_0}),u(s,x),\\ {\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x)\left)\right]d{B}_s,\end{array}$$

(1.1)

where ${\hat{\sigma }}^{\ast }$ is the transpose of $\hat{\sigma }$ which is defined by $\hat{\sigma }:=E[\sigma (s,X_s^{0,x_0},x)]$, and ℒ is a second-order differential operator given by ${(\mathcal{L}u)}_i={(L{u}_i)}_{1\le i\le n}$ with

$$L:=\frac{1}{2}\sum _{i,j=1}^d{a}_{ij}\frac{{\partial }^2}{\partial x_i\partial x_j}+\sum _{i=1}^{d}E\left[b_i(t,X_t^{0,x_0},x)\right]\frac{\partial }{\partial x_i},$$

and

$$a:=(a_{i,j})=\left(E\left[\sigma (t,X_t^{0,x_0},x)\right]E{\left[\sigma (t,X_t^{0,x_0},x)\right]}^{\ast }\right).$$

Here, the function $u(t,x):[0,T]\times {\mathbb{R}}^d\to {\mathbb{R}}^n$ is the unknown function, and $\{B_t,0\le t\le T\}$ is an l-dimensional Brownian motion process defined on a given complete probability space $(\mathrm{\Omega },\mathcal{F},P)$. $X_t^{0,x_0}$, a stochastic process starting at $x_0$ when $t=0$, is the solution of one class of stochastic differential equations (SDEs), and E denotes expectation with respect to the probability P. In this paper, we call this kind of equations (1.1) McKean-Vlasov SPDEs, because they are analogous to McKean-Vlasov PDEs except the stochastic term $d{B}_t$.

McKean-Vlasov PDEs involving models of large stochastic particle systems with mean-field interaction have been studied by stochastic methods in recent years (see [1–4] and the references therein). Mean-field approaches have applications in many areas such as statistical mechanics and physics, quantum mechanics and quantum chemistry. Recently, Lasry and Lions introduced mean-field approaches for high-dimensional systems of evolution equations corresponding to a large number of ‘agents’ or ‘particles’. They extended the field of such mean-field approaches to problems in economics, finance and game theory (see [5] and the references therein).

As is well known, to give a probabilistic representation (Feynman-Kac formula) of quasilinear parabolic SPDEs, Pardoux and Peng [6] introduced a new class of backward stochastic differential equations (BSDEs) called backward doubly stochastic differential equations which have two different types of stochastic integrals: a standard (forward) stochastic integral $d{W}_t$ and a backward stochastic integral $d{B}_t$. They proved the existence and uniqueness for solutions of BDSDEs under uniformly Lipschitz coefficients. When the coefficients are smooth enough, they also established the connection between BDSDEs and a certain kind of quasilinear SPDEs. BDSDEs have a practical background in finance. The extra noise B can be regarded as some extra inside information in a derivative security market. Since 1990s, BDSDEs have drawn more attention from many authors (cf. [7–13] and the references therein). Shi, Gu and Liu gave the comparison theorem of BDSDEs and investigated the existence of solutions for BDSDEs with continuous coefficients in [11]. To relax the Lipschitz conditions, Wu and Zhang studied two kinds of BDSDEs under globally (respectively, locally) monotone assumptions and obtained the uniqueness and existence results of the solutions (see [12]).

Mean-field BSDEs are deduced by Buckdahn, Djehiche, Li and Peng [14] when they studied a special mean-field problem with a purely stochastic method. Later, Buckdahn, Li and Peng [15] investigated the properties of these equations in a Markovian framework, obtained the uniqueness of the solutions of mean-field BSDEs as well as the comparison theorem and also gave the viscosity solutions of a class of McKean-Vlasov PDEs in terms of mean-field BSDEs.

In this paper, we study a new type of BDSDEs, that is, the so called mean-field BDSDEs, under the globally (respectively locally) monotone coefficients. We obtain the existence and uniqueness result of the solution by virtue of the technique proposed by Wu and Zhang [12] and the contraction mapping theorem under certain conditions. Also, the comparison principle for mean-field BDSDEs is discussed when the coefficients satisfy some stricter assumptions. A comparison theorem is a useful result in the theory of BSDEs. For instance, it can be used to study viscosity solutions of PDEs. Here, we point out that it is more delicate to prove the comparison theorem for mean-field BDSDEs because of the mean-field term.

We also present the connection between McKean-Vlasov SPDEs and mean-field BDSDEs. In detail, let $\{X_s^{t,x},t\le s\le T\}$ be the solution of

$$\{\begin{array}{c}d{X}_s^{t,x}=E^{\prime }[b(s,{(X_s^{0,x_0})}^{\prime },X_s^{t,x})]ds+E^{\prime }[\sigma (s,{(X_s^{0,x_0})}^{\prime },X_s^{t,x})]d{W}_s,s\in [t,T],\hfill \\ X_t^{t,x}=x.\hfill \end{array}$$

Assume that Eq. (1.1) has a classical solution. Then the couple $(Y_s^{t,x},Z_s^{t,x})$, where $Y_s^{t,x}=u(s,X_s^{t,x})$ and $Z_s^{t,x}=E^{\prime }{[\sigma (s,{(X_s^{0,x_0})}^{\prime },X_s^{t,x})]}^{\ast }\cdot Du(s,X_s^{t,x})$, verifies the following mean-field BDSDE :

$$\begin{array}{rcl}{Y}_s^{t,x}& =& E^{\prime }\left[\mathrm{\Phi }({\left(X_T^{0,x_0}\right)}^{\prime },X_T^{t,x})\right]+{\int }_s^T{E}^{\prime }\left[f(r,{\left(X_r^{0,x_0}\right)}^{\prime },X_r^{t,x},{\left(Y_r^{0,x_0}\right)}^{\prime },Y_r^{t,x},{\left(Z_r^{0,x_0}\right)}^{\prime },Z_r^{t,x})\right]dr\\ +{\int }_s^T{E}^{\prime }\left[g(r,{\left(X_r^{0,x_0}\right)}^{\prime },X_r^{t,x},{\left(Y_r^{0,x_0}\right)}^{\prime },Y_r^{t,x},{\left(Z_r^{0,x_0}\right)}^{\prime },Z_r^{t,x})\right]d{B}_r\\ -{\int }_s^T{Z}_r^{t,x}d{W}_r.\end{array}$$

(1.2)

In Eq. (1.2), the integral $d{W}_t$ is a forward Itô integral, and the integral $d{B}_t$ denotes a backward Itô integral. $\{W_t,0\le t\le T\}$ and $\{B_t,0\le t\le T\}$ are two mutually independent standard Brownian motion processes with values respectively in ${\mathbb{R}}^d$ and in ${\mathbb{R}}^l$. This conclusion gives a probabilistic representation of McKean-Vlasov SPDEs (1.1), which can be regarded as a stochastic Feynman-Kac formula for Mckean-Vlasov SPDEs.

Our paper is organized as follows. In Section 2, we present the existence and uniqueness results about mean-field BDSDEs with globally monotone coefficients. We investigate the properties of mean-field BDSDEs with locally monotone assumptions in Section 3. We first prove the existence and uniqueness of the solutions of mean-field BDSDEs and then derive the comparison theorem when the mean-field BDSDEs are one-dimensional. In Section 4, we introduce the decoupled mean-field forward-backward doubly stochastic differential equation and study the regularity of its solution with respect to x, which is the initial condition of the McKean-Vlasov SDE. Finally, Section 5 is devoted to the formulation of McKean-Vlasov SPDEs and provides the relationship between the solutions of SPDEs and those of mean-field BDSDEs.

2 Mean-field BDSDEs with globally monotone coefficients

In this section, we study mean-field BDSDEs with globally monotone coefficients, which is helpful for the case of locally monotone coefficients. To this end, we firstly introduce some notations and recall some results on mean-field BSDEs obtained by Buckdahn, Li and Peng [15].

Let $\{W_t,0\le t\le T\}$ and $\{B_t,0\le t\le T\}$ be two mutually independent standard Brownian motion processes, with values respectively in ${\mathbb{R}}^d$ and ${\mathbb{R}}^l$, defined over some complete probability space $(\mathrm{\Omega },\mathcal{F},P)$, where T is a fixed positive number throughout this paper. Moreover, let $\mathcal{N}$ denote the class of P-null sets of ℱ. For each $0\le s\le T$, we define

$${\mathcal{F}}_t\triangleq {\mathcal{F}}_{0,t}^W\vee {\mathcal{F}}_{t,T}^B$$

with ${\mathcal{F}}_{s,t}^W=\sigma \{W_r;s\le r\le t\}\vee \mathcal{N}$ and ${\mathcal{F}}_{t,s}^B=\sigma \{B_r-B_t;t\le r\le s\}\vee \mathcal{N}$.

Note that $\{{\mathcal{F}}_t,t\in [0,T]\}$ is not an increasing family of σ-fields, so it is not a filtration.

We will also use the following spaces:

• For any $n\in \mathbb{N}$, let ${\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n)$ denote the set of (classes of $dP\times dt$ a.e. equal) n-dimensional jointly measurable random processes $\{{\psi }_t;t\in [0,T]\}$ which satisfy: Evidently, ${\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n)$ is a Banach space endowed with the canonical norm $\parallel \psi \parallel ={\{E{\int }_0^T{|{\psi }_s|}^{2}ds\}}^{\frac{1}{2}}$.

• (i) $E{\int }_0^T{|{\psi }_t|}^{2}dt<+\mathrm{\infty }$,

• (ii) ${\psi }_t$ is ${\mathcal{F}}_t$ measurable, for a.e. $0\le t\le T$.

• We denote similarly by ${\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)$ the set of continuous n-dimensional random processes $\{{\psi }_t;t\in [0,T]\}$ which satisfy:

• (i) $E({sup}_{0\le t\le T}{|{\psi }_t|}^2)<+\mathrm{\infty }$,

• (ii) ${\psi }_t$ is ${\mathcal{F}}_t$ measurable, for a.e. $0\le t\le T$.

• $L^0(\mathrm{\Omega },\mathcal{F},P;{\mathbb{R}}^n)$ denotes the space of all ${\mathbb{R}}^n$ valued ℱ-measurable random variables.

• For $1\le p<\mathrm{\infty }$, $L^p(\mathrm{\Omega },\mathcal{F},P;{\mathbb{R}}^n)$ is the space of all ${\mathbb{R}}^n$ valued ℱ-measurable random variables such that $E[{|\xi |}^p]<\mathrm{\infty }$.

Let $(\overline{\mathrm{\Omega }},\overline{\mathcal{F}},\overline{P})=(\mathrm{\Omega }\times \mathrm{\Omega },\mathcal{F}\otimes \mathcal{F},P\otimes P)$ be the (non-completed) product of $(\mathrm{\Omega },\mathcal{F},P)$ with itself, and we define $\overline{\mathbb{F}}=\{{\overline{\mathcal{F}}}_t=\mathcal{F}\otimes {\mathcal{F}}_t,0\le t\le T\}$ on this product space. A random variable $\xi \in L^0(\mathrm{\Omega },\mathcal{F},P;{\mathbb{R}}^n)$ originally defined on Ω is extended canonically to $\overline{\mathrm{\Omega }}:{\xi }^{\prime }({\omega }^{\prime },\omega )=\xi ({\omega }^{\prime })$, $({\omega }^{\prime },\omega )\in \overline{\mathrm{\Omega }}=\mathrm{\Omega }\times \mathrm{\Omega }$. For any $\theta \in L^1(\overline{\mathrm{\Omega }},\overline{\mathcal{F}},\overline{P})$, the variable $\theta (\cdot ,\omega ):\mathrm{\Omega }\to {\mathbb{R}}^n$ belongs to $L^1(\mathrm{\Omega },\mathcal{F},P)$, $P(d\omega )$-a.s., whose expectation is denoted by

$$E^{\prime }[\theta (\cdot ,\omega )]={\int }_{\mathrm{\Omega }}\theta ({\omega }^{\prime },\omega )P\left(d{\omega }^{\prime }\right).$$

Notice that $E^{\prime }[\theta ]=E^{\prime }[\theta (\cdot ,\omega )]\in L^1(\mathrm{\Omega },\mathcal{F},P)$ and

$$\overline{E}[\theta ](={\int }_{\overline{\mathrm{\Omega }}}\theta d\overline{P}={\int }_{\mathrm{\Omega }}{E}^{\prime }[\theta (\cdot ,\omega )]P(d\omega ))=E[E^{\prime }[\theta ]].$$

Moreover, for all $(y^{\prime },z^{\prime },y,z)$, $f=f({\omega }^{\prime },\omega ,t,y^{\prime },z^{\prime },y,z):\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\to {\mathbb{R}}^n$, $g=g({\omega }^{\prime },\omega ,t,y^{\prime },z^{\prime },y,z):\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\to {\mathbb{R}}^{n\times l}$ are two ${\overline{\mathcal{F}}}_t$-measurable functions which satisfy

Assumption 2.1 (A1) $g(t,0,0,0,0)\in {\mathcal{H}}_{\overline{\mathbb{F}}}^2(0,T;{\mathbb{R}}^{n\times l})$, and there exist $L>0$ and $0<\alpha <\frac{1}{2}$ such that

(A2) for any fixed $({\omega }^{\prime },\omega ,t)$, $f({\omega }^{\prime },\omega ,t,\cdot ,\cdot ,\cdot ,\cdot )$ is continuous;

(A3) there exist a process ${\overline{f}}_t\in {\mathcal{H}}_{\overline{\mathbb{F}}}^2(0,T;\mathbb{R})$ and a constant $L>0$ such that

$$\left|f(t,y^{\prime },z^{\prime },y,z)\right|\le {\overline{f}}_t+L(\left|y^{\prime }\right|+\left|z^{\prime }\right|+|y|+|z|);$$

(A4) there exist constants ${\lambda }_1,{\lambda }_2\in \mathbb{R}$ such that for all $t\in [0,T]$, $y_i,y_i^{\prime }\in {\mathbb{R}}^n$, $z_i,z_i^{\prime }\in {\mathbb{R}}^{n\times d}$ ($i=1,2$),

$$(y_1-y_2)(f(t,y_1^{\prime },z^{\prime },y_1,z)-f(t,y_2^{\prime },z^{\prime },y_2,z))\le {\lambda }_1(y_1-y_2)(y_1^{\prime }-y_2^{\prime })+{\lambda }_2{|y_1-y_2|}^2;$$

(A5) there exists $L>0$ such that, $\overline{P}$-a.s., for all $t\in [0,T]$, $y^{\prime },y\in {\mathbb{R}}^n$, $z_1,z_2,z_1^{\prime },z_2^{\prime }\in {\mathbb{R}}^{n\times d}$,

$${|f(t,y^{\prime },z_1^{\prime },y,z_1)-f(t,y^{\prime },z_2^{\prime },y,z_2)|}^2\le L({|z_1^{\prime }-z_2^{\prime }|}^2+{|z_1-z_2|}^2).$$

We now consider the following mean-field BDSDEs with the form:

$$\begin{array}{rcl}{Y}_t& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)\right]ds+{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)\right]d{B}_s\\ -{\int }_t^T{Z}_{s}d{W}_s,0\le t\le T.\end{array}$$

(2.1)

Remark 2.1 Due to our notation, the coefficients of (2.1) are interpreted as follows:

Remark 2.2 If coefficient f meets the following Lipschitz assumption: There exists a constant $L>0$ such that, $\overline{P}$-a.s., for all $t\in [0,T]$, $y_i,y_i^{\prime }\in {\mathbb{R}}^n$, $z_i,z_i^{\prime }\in {\mathbb{R}}^{n\times d}$ ($i=1,2$),

$${|f(t,y_1^{\prime },z_1^{\prime },y_1,z_1)-f(t,y_2^{\prime },z_2^{\prime },y_2,z_2)|}^2\le L({|y_1^{\prime }-y_2^{\prime }|}^2+{|z_1^{\prime }-z_2^{\prime }|}^2+{|y_1-y_2|}^2+{|z_1-z_2|}^2),$$

then it must satisfy conditions (A4) and (A5).

Definition 2.1 A pair of ${\mathcal{F}}_t$-measurable processes $\{(Y_t,Z_t);0\le t\le T\}$ is called a solution of mean-field BDSDE (2.1) if $(Y,Z)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$ and it satisfies mean-field BDSDE (2.1).

The main result of this section is the following theorem.

Theorem 2.1 For any random variable $\xi \in L^2(\mathrm{\Omega },{\mathcal{F}}_T,P;{\mathbb{R}}^n)$, under Assumption  2.1, mean-field BDSDE (2.1) admits a unique solution $(Y,Z)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$.

Proof Step 1: For any $(y,z)\in {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$, BDSDE

$$\begin{array}{rcl}{Y}_t& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f(s,y_s^{\prime },z_s^{\prime },Y_s,Z_s)\right]ds+{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,y_s^{\prime },z_s^{\prime },Y_s,Z_s)\right]d{B}_s\\ -{\int }_t^T{Z}_{s}d{W}_s,0\le t\le T\end{array}$$

(2.2)

has a unique solution. In order to get this conclusion, we define

$${\phi }^{(y,z)}(s,\mu ,\nu ):=E^{\prime }\left[\phi (s,y_s^{\prime },z_s^{\prime },\mu ,\nu )\right],\text{for }\phi =f,g.$$

Then (2.2) can be rewritten as

$$Y_t=\xi +{\int }_t^T{f}^{(y,z)}(Y_s,Z_s)ds+{\int }_t^T{g}^{(y,z)}(Y_s,Z_s)d{B}_s-{\int }_t^T{Z}_{s}d{W}_s.$$

Due to Assumption 2.1, for all $(\mu ,\nu ),({\mu }_1,{\nu }_1),({\mu }_2,{\nu }_2)\in {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}$, g satisfies

$${|g^{(y,z)}({\mu }_1,{\nu }_1)-g^{(y,z)}({\mu }_2,{\nu }_2)|}^2\le L{|{\mu }_1-{\mu }_2|}^2+\alpha {|{\nu }_1-{\nu }_2|}^2,$$

and f fulfills

According to Theorem 2.2 in [12], BDSDE (2.2) has a unique solution.

Step 2: Now, we introduce a norm on the space ${\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$ which is equivalent to the canonical norm

$${\parallel (y,z)\parallel }_{\beta }={\left\{E{\int }_0^T{e}^{\beta s}(\overline{c}{|y_s|}^2+{|z_s|}^2)ds\right\}}^{\frac{1}{2}},\overline{c},\beta >0.$$

The parameters $\overline{c}$ and β are specified later.

From Step 1, we can introduce the mapping $(Y_{\cdot },Z_{\cdot })=I[(y_{\cdot }^{\prime },z_{\cdot }^{\prime })]:{\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})\to {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$ through the equation

$$\begin{array}{rcl}{Y}_t& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f(s,y_s^{\prime },z_s^{\prime },Y_s,Z_s)\right]ds+{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,y_s^{\prime },z_s^{\prime },Y_s,Z_s)\right]d{B}_s\\ -{\int }_t^T{Z}_{s}d{W}_s,0\le t\le T.\end{array}$$

For any $(y^1,z^1),(y^2,z^2)\in {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$, we set $(Y^1,Z^1)=I[(y^1,z^1)]$, $(Y^2,Z^2)=I[(y^2,z^2)]$, $(\overline{y},\overline{z})=(y^1-y^2,z^1-z^2)$ and $(\overline{Y},\overline{Z})=(Y^1-Y^2,Z^1-Z^2)$. Then applying Itô’s formula to $e^{\beta s}{|{\overline{Y}}_s|}^2$ and by virtue of $Y^1,Y^2\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)$, we have

(2.3)

From condition (A4) and noting that $E^{\prime }[Y_s({\omega }^{\prime })]=E[Y_s(\omega )]$, for any $M>0$, we get

Then we have

If we set $M=\frac{2L}{1-2\alpha }$, $\overline{c}=\frac{4}{1+2\alpha }(\frac{|{\lambda }_1|}{M}+L)$, $\beta =|{\lambda }_1|M+2{\lambda }_2^{+}+3M+L+\frac{1}{2}\overline{c}$, then it yields

$$E\left[{\int }_t^T{e}^{\beta s}(\overline{c}{|{\overline{Y}}_s|}^2+{|{\overline{Z}}_s|}^2)ds\right]\le \frac{1+2\alpha }{2}E\left[{\int }_t^T{e}^{\beta s}(\overline{c}{|{\overline{y}}_s|}^2+{|{\overline{z}}_s|}^2)ds\right].$$

Consequently, I is a strict contraction on ${\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$ equipped with the norm ${\parallel \cdot \parallel }_{\beta }$ for $0<\alpha <\frac{1}{2}$. With the contraction mapping theorem, there admits a unique fixed point $(Y,Z)\in {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n\times {\mathbb{R}}^{n\times d})$ such that $I(Y,Z)=(Y,Z)$. On the other hand, from Step 1, we know that if $I(Y,Z)=(Y,Z)$, then $(Y,Z)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$, which is the unique solution of Eq. (2.1). □

Suppose that: For some $f:\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\to {\mathbb{R}}^n$ satisfying (A2)-(A5), the generators $f_i$, $i=1,2$ are of the form

$$f_i(s,{\left(Y_s^i\right)}^{\mathrm{\prime }},{\left(Z_s^i\right)}^{\mathrm{\prime }},Y_s^i,Z_s^i)=f(s,{\left(Y_s^i\right)}^{\mathrm{\prime }},{\left(Z_s^i\right)}^{\mathrm{\prime }},Y_s^i,Z_s^i)+{\phi }_i(s),dsd\overline{P}\text{-a.e.},i=1,2,$$

where ${\phi }_i\in {\mathcal{H}}_{\overline{\mathbb{F}}}^2(0,T;{\mathbb{R}}^n)$. Then we have the following corollary.

Corollary 2.1 Suppose that $(Y^i,Z^i)$ is the solution of mean-field BDSDE (2.1) with data $({\xi }^i,f_i,g)$, $i=1,2$, where ${\xi }^1,{\xi }^2\in L^2(\mathrm{\Omega },{\mathcal{F}}_T,P;{\mathbb{R}}^n)$ are two arbitrary terminal values. The difference of $(Y^1,Z^1)$ and $(Y^2,Z^2)$ satisfies the following estimate:

(2.4)

where $\beta =2|{\lambda }_1|+2{\lambda }_2^{+}+\frac{4L}{1-2\alpha }+2+2L$.

The proof of the above corollary is similar to that of Theorem 2.1 and is therefore omitted.

3 Mean-field BDSDEs with locally monotone coefficients

In this section, we investigate mean-field BDSDEs with locally monotone coefficients. The results can be regarded as an extension of the results in [12] to the mean-field type.

We assume

(A3′) there exist $L>0$ and $0\le \gamma <1$ such that $|f(t,y^{\prime },z^{\prime },y,z)|\le L(1+{|y^{\prime }|}^{\gamma }+{|z^{\prime }|}^{\gamma }+{|y|}^{\gamma }+{|z|}^{\gamma })$;

(A4′) for any $N\in \mathbb{N}$, there exist constants ${\lambda }_N,{\overline{\lambda }}_N\in \mathbb{R}$ such that, $\mathrm{\forall }{y}_i^{\prime },y_i,z^{\prime },z$ satisfying $|y_i^{\prime }|,|y_i|,|z^{\prime }|,|z|\le N$ ($i=1,2$), we have

$$(y_1-y_2)(f(t,y_1^{\prime },z^{\prime },y_1,z)-f(t,y_2^{\prime },z^{\prime },y_2,z))\le {\lambda }_N(y_1-y_2)(y_1^{\prime }-y_2^{\prime })+{\overline{\lambda }}_N{|y_1-y_2|}^2;$$

(A5′) $\mathrm{\forall }N\in \mathbb{N}$, there exists $L_N>0$ such that, for any $y^{\prime }$, y, $z_i^{\prime }$, $z_i$ satisfying $|y^{\prime }|,|y|,|z_i^{\prime }|,|z_i|\le N$ ($i=1,2$), it holds

$${|f(t,y^{\prime },z_1^{\prime },y,z_1)-f(t,y^{\prime },z_2^{\prime },y,z_2)|}^2\le L_N({|z_1^{\prime }-z_2^{\prime }|}^2+{|z_1-z_2|}^2).$$

Remark 3.1 Since ${|x|}^{\gamma }\le 1+|x|$, $\gamma \in [0,1)$, (A3′) implies that

$$\left|f(t,y^{\prime },z^{\prime },y,z)\right|\le L(5+\left|y^{\prime }\right|+\left|z^{\prime }\right|+|y|+|z|).$$

We need the following lemma, which plays an important role in the proof of the main result.

Lemma 3.1 Under (A2), (A3′)-(A5′) there exists a sequence of ${\{f_m\}}_{m=1}^{\mathrm{\infty }}$ such that

• (i) for fixed $m\in \mathbb{N}$, ${\omega }^{\prime }$, ω, t, $f_m({\omega }^{\prime },\omega ,t,\cdot ,\cdot ,\cdot ,\cdot )$ is continuous;

• (ii) ∀m, $|f_m(t,y^{\prime },z^{\prime },y,z)|\le |f(t,y^{\prime },z^{\prime },y,z)|\le L(1+{|y^{\prime }|}^{\gamma }+{|z^{\prime }|}^{\gamma }+{|y|}^{\gamma }+{|z|}^{\gamma })$;

• (iii) ∀N, ${\rho }_N(f_m-f)\to 0$ as $m\to \mathrm{\infty }$, where ${\rho }_m^2(f):=E[{\int }_0^T{sup}_{|y^{\prime }|,|z^{\prime }|,|y|,|z|\le m}{|f(t,y^{\prime },z^{\prime },y,z)|}^{2}dt]$;

• (iv) ∀m, $f_m$ is globally monotone in y; moreover, for any m, N with $m\ge N$, it holds that

  $$(y_1-y_2)(f_m(t,y_1^{\prime },z^{\prime },y_1,z)-f_m(t,y_2^{\prime },z^{\prime },y_2,z))\le {\lambda }_N(y_1-y_2)(y_1^{\prime }-y_2^{\prime })+{\overline{\lambda }}_N{|y_1-y_2|}^2,$$

for any t, $y_i^{\prime }$, $y_i$, $z^{\prime }$, z satisfying $|y_i^{\prime }|,|y_i|,|z^{\prime }|,|z|\le N$ ($i=1,2$);

• (v) ∀m, $f_m$ is globally Lipschitz in $z^{\prime }$, z; moreover, for any m, N with $m\ge N$, it holds that

  $${|f_m(t,y^{\prime },z_1^{\prime },y,z_1)-f_m(t,y^{\prime },z_2^{\prime },y,z_2)|}^2\le L_N({|z_1^{\prime }-z_2^{\prime }|}^2+{|z_1-z_2|}^2),$$

for any t, $y^{\prime }$, y, $z_i^{\prime }$, $z_i$ satisfying $|y^{\prime }|,|y|,|z_i^{\prime }|,|z_i|\le N$ ($i=1,2$).

Proof We define $f_m$ by

$$f_m(t,y^{\prime },z^{\prime },y,z)=f(t,y^{\prime },z^{\prime },y,z){\varphi }_m\left(y^{\prime }\right){\phi }_m\left(z^{\prime }\right){\psi }_m(y){\eta }_m(z),$$

where ${\varphi }_m:{\mathbb{R}}^n\to {\mathbb{R}}^{+}$ is a sequence of smooth functions such that $0\le {\varphi }_m\le 1$, ${\varphi }_m(x)=1$ for $|x|\le m$, and ${\varphi }_m(x)=0$ for $|x|\ge m+1$. Similarly, we define the sequences ${\phi }_m:{\mathbb{R}}^{n\times d}\to {\mathbb{R}}^{+}$, ${\psi }_m:{\mathbb{R}}^n\to {\mathbb{R}}^{+}$, ${\eta }_m:{\mathbb{R}}^{n\times d}\to {\mathbb{R}}^{+}$. It should be pointed out that ${\varphi }_m$, ${\phi }_m$, ${\psi }_m$ and ${\eta }_m$ are continuously differentiable with bounded derivatives for each m. The conclusion of this lemma can be easily obtained by arguments similar to those of Lemma 3.3 in [12]. □

We now present the main result of this section.

Theorem 3.1 Let (A1), (A2), (A3′)-(A5′) hold. Assume, moreover,

$$\frac{1+exp(2L+2|{\lambda }_N|+2{\overline{\lambda }}_N^{+}+2L_N{\theta }^{-1}+2)}{N^{2(1-\gamma )}}\to 0,\mathit{\text{as}}N\to \mathrm{\infty },$$

(3.1)

where θ is an arbitrarily fixed constant such that $0<\theta <1-2\alpha$. Then mean-field BDSDE (2.1) has a unique solution $(Y,Z)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$.

Proof We now construct an approximate sequence. Let $f_m$ be associated to f by Lemma 3.1. Then for each m, $f_m$ is globally monotone in y and globally Lipschitz in z. By Theorem 2.1, the following mean-field BDSDE

$$\begin{array}{rcl}{Y}_t^m& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f_m(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^m,Z_s^m)\right]ds\\ +{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^m,Z_s^m)\right]d{B}_s-{\int }_t^T{Z}_s^{m}d{W}_s,0\le t\le T,\end{array}$$

(3.2)

admits a unique solution $(Y^m,Z^m)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$ for each $m\ge N$. Applying Itô’s formula to ${|Y_t^m|}^2$ yields

where

and

Hence,

Then it follows from Gronwall’s inequality and the B-D-G inequality that

where $C>0$ only depends on T, α, L and is independent of m.

For any $m,k\in \mathbb{N}$, set

$$\begin{array}{rcl}A& :=& \{({\omega }^{\prime },\omega ,s):\left|{\left(Y_s^m\right)}^{\prime }\right|+\left|{\left(Z_s^m\right)}^{\prime }\right|+\left|{\left(Y_s^k\right)}^{\prime }\right|+\left|{\left(Z_s^k\right)}^{\prime }\right|\\ +\left|Y_s^m\right|+\left|Z_s^m\right|+\left|Y_s^k\right|+\left|Z_s^k\right|\ge N\},\end{array}$$

and $\overline{A}:=\mathrm{\Omega }\setminus A$.

Next, we will conclude that $(Y^m,Z^m)$ is a Cauchy sequence in ${\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$. Actually, since mean-field BDSDE

$$\begin{array}{rcl}{Y}_t^k& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f_k(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^k\right)}^{\mathrm{\prime }},Y_s^k,Z_s^k)\right]ds+{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^k\right)}^{\mathrm{\prime }},Y_s^k,Z_s^k)\right]d{B}_s\\ -{\int }_t^T{Z}_s^{k}d{W}_s,0\le t\le T,\end{array}$$

admits a unique solution $(Y^k,Z^k)\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$ for each $k\ge N$. Applying Itô’s formula to ${|Y_t^m-Y_t^k|}^2$, we have

(3.3)

where

We next estimate I, II and III.

For the first term I, based on Hölder’s inequality and Chebyshev’s inequality, we have

$$\begin{array}{rcl}\mathrm{I}& \le & E{\int }_t^T{|Y_s^m-Y_s^k|}^{2}ds\\ +E\left[{\int }_t^T{E}^{\mathrm{\prime }}\left[{|f_m(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^m,Z_s^m)-f_k(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^k\right)}^{\mathrm{\prime }},Y_s^k,Z_s^k)|}^2\right]{\mathbb{I}}_{A}ds\right]\\ \le & E{\int }_t^T{|Y_s^m-Y_s^k|}^{2}ds+C{N}^{-2(1-\gamma )},\end{array}$$

(3.4)

where $C>0$ depends on T, L, α and $E[{\int }_0^T{|E^{\prime }[g(s,0,0,0,0)]|}^{2}ds]$.

For the second term II, due to the local monotonicity of $f_m$ in y and the local Lipschitz condition of $f_m$ in z, we obtain that for $\mathrm{\forall }M>0$, the following holds:

$$\begin{array}{rcl}\mathrm{II}& =& 2E[{\int }_t^T(Y_s^m-Y_s^k)\cdot E^{\mathrm{\prime }}[f_m(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^m,Z_s^m)\\ -f_m(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^k,Z_s^m)\left]{\mathbb{I}}_{\overline{A}}ds\right]\\ +2E[{\int }_t^T(Y_s^m-Y_s^k)\cdot E^{\mathrm{\prime }}[f_m(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^k,Z_s^m)\\ -f_m(s,{\left(Y_s^k\right)}^{\mathrm{\prime }},{\left(Z_s^k\right)}^{\mathrm{\prime }},Y_s^k,Z_s^k)\left]{\mathbb{I}}_{\overline{A}}ds\right]\\ \le & 2E{\int }_t^T[{\lambda }_N(Y_s^m-Y_s^k)E(Y_s^m-Y_s^k)+{\overline{\lambda }}_N{|Y_s^m-Y_s^k|}^2]ds\\ +ME{\int }_t^T{|Y_s^m-Y_s^k|}^{2}ds+\frac{L_N}{M}E{\int }_t^T[E^{\prime }\left[{|{\left(Z_s^m\right)}^{\prime }-{\left(Z_s^k\right)}^{\prime }|}^2\right]+{|Z_s^m-Z_s^k|}^2]ds\\ \le & (2|{\lambda }_N|+2{\overline{\lambda }}_N^{+}+M)E{\int }_t^T{|Y_s^m-Y_s^k|}^{2}ds+\frac{2L_N}{M}E{\int }_t^T{|Z_s^m-Z_s^k|}^{2}ds.\end{array}$$

(3.5)

For the last term, we have

$$\mathrm{III}\le E{\int }_t^T{|Y_s^m-Y_s^k|}^{2}ds+{\rho }_N^2(f_m-f_k).$$

(3.6)

Choose $M>0$ such that $\theta :=\frac{2L_N}{M}<1-2\alpha$. Then from (3.3)-(3.6), we obtain

Applying Gronwall’s inequality and the B-D-G inequality to the above inequality yields

where $c>0$ is independent of m, k. Now passing to the limit successively on m, k and N, we see that $(Y^m,Z^m)$ is a Cauchy (hence convergent) sequence in $\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$; denote the limit by $(Y,Z)$, which satisfies

$$E\left[\underset{0\le t\le T}{sup}{|Y_t^m-Y_t|}^2\right]+E\left[{\int }_0^T{|Z_s^m-Z_s|}^{2}ds\right]\to 0$$

as $m\to \mathrm{\infty }$.

Next, we show that $(Y,Z)$ is the solution of mean-field BDSDE (2.1). To this end, we only need to prove that the following conclusion holds along a subsequence:

(3.7)

Set

$$A_m:=\{({\omega }^{\prime },\omega ,s):\left|{\left(Y_s^m\right)}^{\prime }\right|+\left|{\left(Z_s^m\right)}^{\prime }\right|+\left|Y_s^{\mathrm{\prime }}\right|+\left|Z_s^{\mathrm{\prime }}\right|+\left|Y_s^m\right|+\left|Z_s^m\right|+|Y_s|+|Z_s|\ge N\},$$

and ${\overline{A}}_m:=\mathrm{\Omega }\setminus A_m$.

Since

$$f_m(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},{\left(Z_s^m\right)}^{\mathrm{\prime }},Y_s^m,Z_s^m)-f(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)=I_1(m,s)+I_2(m,s)+I_3(m,s)+I_4(m,s),$$

where

then we have

(3.8)

where $C>0$ is independent of m. As

$$E\left[\underset{0\le t\le T}{sup}{|Y_t^m-Y_t|}^2\right]+E\left[{\int }_0^T{|Z_s^m-Z_s|}^{2}ds\right]\to 0\text{and}\underset{m\ge N}{sup}E\left[\underset{0\le t\le T}{sup}{\left|Y_t^m\right|}^2\right]<\mathrm{\infty },$$

there exists a subsequence of $Y^m$, still denoted by $Y^m$, such that $Y_t^m\to Y_t$ a.e., a.s. It then follows from the continuity of f in y and the dominated convergence theorem that

$$E\left[{\int }_t^T{E}^{\mathrm{\prime }}\left[{|f(s,{\left(Y_s^m\right)}^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s^m,Z_s)-f(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)|}^2\right]ds\right]\to 0$$

as $m\to \mathrm{\infty }$.

Now, passing to the limit as $m\to \mathrm{\infty }$ and $N\to \mathrm{\infty }$ in (3.8) successively, it follows that (3.7) holds. Then letting $m\to \mathrm{\infty }$ in (3.2) yields

$$\begin{array}{rcl}{Y}_t& =& \xi +{\int }_t^T{E}^{\mathrm{\prime }}\left[f(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)\right]ds+{\int }_t^T{E}^{\mathrm{\prime }}\left[g(s,Y_s^{\mathrm{\prime }},Z_s^{\mathrm{\prime }},Y_s,Z_s)\right]d{B}_s\\ -{\int }_t^T{Z}_{s}d{W}_s,0\le t\le T.\end{array}$$

Therefore, we come to the conclusion of this theorem. □

Now, we discuss the comparison theorem for mean-field BDSDEs. We only consider one-dimensional mean-field BDSDEs, i.e., $n=1$.

We consider the following mean-field BDSDEs: ($0\le t\le T$)

(3.9)

(3.10)

Theorem 3.2 (Comparison theorem)

Assume mean-field BDSDEs (3.9) and (3.10) satisfy the conditions of Theorem  3.1. Let $(Y^1,Z^1)$ and $(Y^2,Z^2)$ be the solutions of mean-field BDSDEs (3.9) and (3.10), respectively. Moreover, for the two generators of $f_1$ and $f_2$, we suppose:

• (i) One of the two generators is independent of $z^{\prime }$.

• (ii) One of the two generators is nondecreasing in $y^{\prime }$.

Then if ${\xi }^1\le {\xi }^2$, a.s., $f_1(t,y^{\prime },z^{\prime },y,z)\le f_2(t,y^{\prime },z^{\prime },y,z)$, a.s., there also holds that $Y_t^1\le Y_t^2$, a.s. $\mathrm{\forall }t\in [0,T]$.

Remark 3.2 The conditions (i) and (ii) of Theorem 3.2 are, in particular, satisfied if they hold for the same generator $f_j$ ($j=1,2$), but also if (i) is satisfied by one generator and (ii) by the other one.

Proof Without loss of generality, we suppose that (i) is satisfied by $f_1$ and (ii) by $f_2$. For notational simplicity, we set $\overline{\xi }:={\xi }^1-{\xi }^2$, $(\overline{Y},\overline{Z}):=(Y^1-Y^2,Z^1-Z^2)$, then

$$\begin{array}{rcl}{\overline{Y}}_t& =& \overline{\xi }+{\int }_t^T{E}^{\mathrm{\prime }}[f_1(s,{\left(Y_s^1\right)}^{\mathrm{\prime }},Y_s^1,Z_s^1)-f_2(s,{\left(Y_s^2\right)}^{\mathrm{\prime }},{\left(Z_s^2\right)}^{\mathrm{\prime }},Y_s^2,Z_s^2)]ds\\ +{\int }_t^T{E}^{\mathrm{\prime }}[g(s,{\left(Y_s^1\right)}^{\mathrm{\prime }},{\left(Z_s^1\right)}^{\mathrm{\prime }},Y_s^1,Z_s^1)-g(s,{\left(Y_s^2\right)}^{\mathrm{\prime }},{\left(Z_s^2\right)}^{\mathrm{\prime }},Y_s^2,Z_s^2)]d{B}_s\\ -{\int }_t^T{\overline{Z}}_{s}d{W}_s,0\le t\le T.\end{array}$$

By Itô’s formula applied to ${|{\overline{Y}}_t^{+}|}^2$ and noting that ${\xi }^1\le {\xi }^2$, it easily follows that

(3.11)

Since $f_1(t,y^{\prime },z^{\prime },y,z)\le f_2(t,y^{\prime },z^{\prime },y,z)$ a.s. and $f_2$ is nondecreasing in $y^{\prime }$, we have

Then we have

$$\begin{array}{rcl}\mathrm{\Delta }:& =& 2E\left[{\overline{Y}}_s^{+}\left(E^{\mathrm{\prime }}[f_1(s,{\left(Y_s^1\right)}^{\mathrm{\prime }},Y_s^1,Z_s^1)-f_2(s,{\left(Y_s^2\right)}^{\mathrm{\prime }},{\left(Z_s^2\right)}^{\mathrm{\prime }},Y_s^2,Z_s^2)]\right)\right]\\ \le & (2{\overline{\lambda }}_N^{+}+\frac{L_N}{1-2\alpha }+2|{\lambda }_N|)E\left[{\left|{\overline{Y}}_s^{+}\right|}^2\right]+(1-2\alpha )E\left[I_{\{{\overline{Y}}_s>0\}}{|{\overline{Z}}_s|}^2\right].\end{array}$$

(3.12)

With the assumption (A1), we obtain

(3.13)

Combining (3.12), (3.13) with (3.11) yields

$$E\left[{\left|{\overline{Y}}_t^{+}\right|}^2\right]\le (2{\overline{\lambda }}_N^{+}+\frac{L_N}{1-2\alpha }+2|{\lambda }_N|+2L){\int }_t^{T}E\left[{\left({\overline{Y}}_s^{+}\right)}^2\right]ds.$$

By Gronwall’s inequality, it follows that

$$E\left[{\left|{\overline{Y}}_t^{+}\right|}^2\right]=0,\mathrm{\forall }t\in [0,T],$$

that is, $Y_t^1\le Y_t^2$, P-a.s., $\mathrm{\forall }t\in [0,T]$. □

4 Decoupled mean-field forward-backward doubly SDEs

In this section, we study the decoupled mean-field forward-backward doubly stochastic differential equations. First, we recall some results of Buckdahn, Li and Peng [15] on McKean-Vlasov SDEs. Given continuous functions $b:\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^d\times {\mathbb{R}}^d\to {\mathbb{R}}^d$ and $\sigma :\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^d\times {\mathbb{R}}^d\to {\mathbb{R}}^{d\times d}$ which are supposed to satisfy the following conditions:

Assumption 4.1 (i) $b(t,0,0)$ and $\sigma (t,0,0)$ are ${\overline{\mathcal{F}}}_t$-measurable continuous processes and there exists some constant $L>0$ such that

$$\left|b(t,x^{\prime },x)\right|+\left|\sigma (t,x^{\prime },x)\right|\le L(1+|x|),\text{a.s., for all }0\le t\le T,x,x^{\prime }\in {\mathbb{R}}^d;$$

• (ii) b and σ are Lipschitz in x, $x^{\prime }$, i.e., there is some constant $L>0$ such that

  

For any $x_0\in {\mathbb{R}}^d$, we consider the following SDE parameterized by the initial condition $(t,\zeta )\in [0,T]\times L^2(\mathrm{\Omega },{\mathcal{F}}_t,P;{\mathbb{R}}^d)$:

$$\{\begin{array}{c}d{X}_s^{t,\zeta }=E^{\prime }[b(s,{(X_s^{0,x_0})}^{\prime },X_s^{t,\zeta })]ds+E^{\prime }[\sigma (s,{(X_s^{0,x_0})}^{\prime },X_s^{t,\zeta })]d{W}_s,s\in [t,T],\hfill \\ X_t^{t,\zeta }=\zeta .\hfill \end{array}$$

(4.1)

From the result about Eq. (5.1) in [15], we know that under Assumption 4.1, SDE (4.1) has a unique strong solution, and we can obtain that $X_T^{t,\zeta }$ has a continuous version with the following well-known standard estimates.

Proposition 4.1 $\mathrm{\forall }p\ge 2$, there exists $C_p\in {\mathbb{R}}^{+}$ such that, for all $t\in [0,T]$ and $\zeta ,{\zeta }^{\prime }\in L^p(\mathrm{\Omega },{\mathcal{F}}_t,P;{\mathbb{R}}^d)$,

(4.2)

for all $\delta >0$ with $t+\delta \le T$.

Now, let $f(t,x^{\prime },x,y^{\prime },y,z^{\prime },z)$, $g(t,x^{\prime },x,y^{\prime },y,z^{\prime },z)$ and $\mathrm{\Phi }(x^{\prime },x)$ be real-valued functions and satisfy the following conditions.

Assumption 4.2 (i) Φ: $\overline{\mathrm{\Omega }}\times {\mathbb{R}}^d\times {\mathbb{R}}^d\to {\mathbb{R}}^n$ is an ${\overline{\mathcal{F}}}_T\otimes \mathcal{B}({\mathbb{R}}^d)$-measurable random variable, $f:\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^{n\times d}\to {\mathbb{R}}^n$ and $g:\overline{\mathrm{\Omega }}\times [0,T]\times {\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^{n\times d}\to {\mathbb{R}}^{n\times l}$ are two measurable processes such that $f(t,x^{\prime },x,y^{\prime },y,z^{\prime },z)$, $g(t,x^{\prime },x,y^{\prime },y,z^{\prime },z)$ are ${\overline{\mathcal{F}}}_t$-measurable, for all $(x^{\prime },x,y^{\prime },y,z^{\prime },z)\in {\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^{n\times d}$.

• (ii) For all $0\le t\le T$, $x_1^{\prime },x_1,x_2^{\prime },x_2\in {\mathbb{R}}^d$, $y_1^{\prime },y_1,y_2^{\prime },y_2\in {\mathbb{R}}^n$, $z_1^{\prime },z_1,z_2^{\prime },z_2\in {\mathbb{R}}^{n\times d}$, there exist constants $L>0$, ${\lambda }_1,{\lambda }_2\in \mathbb{R}$ and $0<\alpha <\frac{1}{2}$ such that

  

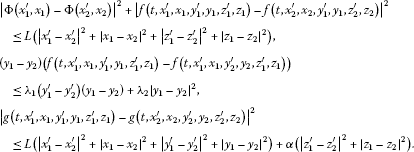
• (iii) f, g and Φ satisfy a linear growth condition, i.e., there exists some $L>0$ such that, a.s., for all $x^{\prime },x\in {\mathbb{R}}^d$

  $$\left|\mathrm{\Phi }(x^{\prime },x)\right|+\left|f(t,x^{\prime },x,0,0,0,0)\right|+\left|g(t,x^{\prime },x,0,0,0,0)\right|\le L(1+|x|+\left|x^{\prime }\right|).$$

Next, we investigate the solution of the following BDSDE:

$$\{\begin{array}{c}-d{Y}_s^{t,\zeta }=E^{\prime }[f(s,{(X_s^{0,x_0})}^{\prime },X_s^{t,\zeta },{(Y_s^{0,x_0})}^{\prime },Y_s^{t,\zeta },{(Z_s^{0,x_0})}^{\prime },Z_s^{t,\zeta })]ds\hfill \\ \phantom{-d{Y}_s^{t,\zeta }=}+E^{\prime }[g(s,{(X_s^{0,x_0})}^{\prime },X_s^{t,\zeta },{(Y_s^{0,x_0})}^{\prime },Y_s^{t,\zeta },{(Z_s^{0,x_0})}^{\prime },Z_s^{t,\zeta })]d{B}_s-Z_s^{t,\zeta }d{W}_s,\hfill \\ Y_T^{t,\zeta }=E^{\prime }[\mathrm{\Phi }({(X_T^{0,x_0})}^{\prime },X_T^{t,\zeta })],s\in [t,T].\hfill \end{array}$$

(4.3)

Firstly, we study the case $(t,\zeta )=(0,x_0)$. From Theorem 2.1, we know that there exists a unique solution $(Y^{0,x_0},Z^{0,x_0})\in {\mathcal{S}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$ to the mean-field BDSDE (4.3). Once we have $(Y^{0,x_0},Z^{0,x_0})$, Eq. (4.3) becomes a classical BDSDE with coefficients

and $\tilde{\mathrm{\Phi }}(\omega ,X_T^{t,\zeta }(\omega ))=E^{\prime }[\mathrm{\Phi }(\cdot ,\omega ,{(X_T^{0,x_0})}^{\prime },X_T^{t,\zeta })]\in L^2(\mathrm{\Omega },{\mathcal{F}}_T,P;{\mathbb{R}}^n)$. Then due to Theorem 2.2 in [12], we obtain that there exists a unique solution $(Y^{t,\zeta },Z^{t,\zeta })\in {\mathcal{S}}_{\mathbb{F}}^2([0,T];{\mathbb{R}}^n)\times {\mathcal{H}}_{\mathbb{F}}^2(0,T;{\mathbb{R}}^{n\times d})$ to Eq. (4.3).

For BDSDE (4.3), we give the following proposition.

Proposition 4.2 For any $t\in [0,T]$ and $\zeta ,{\zeta }^{\prime }\in L^2(\mathrm{\Omega },{\mathcal{F}}_t,P;{\mathbb{R}}^d)$, there exists a constant $C>0$ such that

(4.4)

(4.5)

Proof Combining classical BDSDE estimates (see the proof of Theorem 2.1 in Pardoux and Peng [6]) with the techniques presented in Theorem 3.1, we can get the proof easily. □

5 Mean-field BDSDEs and McKean-Vlasov SPDEs

We now pay attention to investigation of the following system of quasilinear backward stochastic partial differential equations which are called McKean-Vlasov SPDEs: for any $(t,x)\in [0,T]\times {\mathbb{R}}^d$,

$$\begin{array}{rcl}u(t,x)& =& E\left[\mathrm{\Phi }(X_T^{0,x_0},x)\right]+{\int }_t^T\mathcal{L}u(s,x)ds\\ +{\int }_t^{T}E\left[f(s,X_s^{0,x_0},x,u(s,X_s^{0,x_0}),u(s,x),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x))\right]ds\\ +{\int }_t^{T}E\left[g\right(s,X_s^{0,x_0},x,u(s,X_s^{0,x_0}),u(s,x),\\ {\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x)\left)\right]d{B}_s,\end{array}$$

(5.1)

with $\hat{\sigma }:=E[\sigma (s,X_s^{0,x_0},x)]=E^{\prime }[\sigma (s,{(X_s^{0,x_0})}^{\prime },x)]$, and $u:{\mathbb{R}}^{+}\times {\mathbb{R}}^d⟶{\mathbb{R}}^n$,

$$\mathcal{L}u=\left(\begin{array}{c}L{u}_1\\ ⋮\\ L{u}_n\end{array}\right)$$

with

$$L:=\frac{1}{2}\sum _{i,j=1}^d{a}_{ij}\frac{{\partial }^2}{\partial x_i\partial x_j}+\sum _{i=1}^{d}E\left[b_i(t,X_t^{0,x_0},x)\right]\frac{\partial }{\partial x_i},$$

where

$$a:=(a_{i,j})=\left(E\left[\sigma (t,X_t^{0,x_0},x)\right]E{\left[\sigma (t,X_t^{0,x_0},x)\right]}^{\ast }\right).$$

Note that

In fact, Eq. (5.1) is a new kind of nonlocal SPDE because of the mean-field term. Here, the functions b, σ, f, g and Φ are supposed to satisfy Assumption 4.1 and Assumption 4.2 respectively, and $X^{0,x_0}$ is the solution of the mean-field SDE (4.1) with $(t,\xi )=(0,x_0)$.

Now, we give the main theorem of this section.

Theorem 5.1 Suppose that Assumption  4.1 and Assumption  4.2 hold. Let $\{u(t,x);0\le t\le T,x\in {\mathbb{R}}^d\}$ be a ${\mathcal{F}}_{t,T}^B$-measurable random field such that $u(t,x)$ satisfies Eq. (5.1) and for each $(t,x)$, $u\in C^{0,2}([0,T]\times {\mathbb{R}}^d;{\mathbb{R}}^n)$ a.s. Moreover, we assume that $f,g\in C([0,T]\times {\mathbb{R}}^d\times {\mathbb{R}}^d\times {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^{n\times d}\times {\mathbb{R}}^{n\times d})$ for a.s. $\overline{\omega }\in \overline{\mathrm{\Omega }}$.

Then we have $u(t,x)=Y_t^{t,x}$, where ${\{(Y_s^{t,x},Z_s^{t,x});t\le s\le T\}}_{t\ge 0,x\in {\mathbb{R}}^d}$ is the unique solution of the mean-field BDSDEs (4.3) and

$$Y_s^{t,x}=u(s,X_s^{t,x}),Z_s^{t,x}=E^{\prime }{\left[\sigma (s,{\left(X_s^{0,x_0}\right)}^{\prime },X_s^{t,x})\right]}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{t,x}).$$

(5.2)

Proof It suffices to show that $\{u(s,X_s^{t,x}),E^{\prime }{[\sigma (s,{(X_s^{0,x_0})}^{\prime },X_s^{t,x})]}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{t,x});0\le t\le s\}$ solves the mean-field BDSDE (4.3). To simplify the notation, we define

$$\begin{array}{rcl}\hat{\phi }(s,X_s^{0,x_0},x)& \triangleq & E\left[\phi \right(s,X_s^{0,x_0},x,u(s,X_s^{0,x_0}),u(s,x),\\ {\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x)\left)\right],\text{for }\phi =f,g.\end{array}$$

According to our notations introduced in Section 2, we know that

$$\begin{array}{rcl}\hat{\phi }(s,X_s^{0,x_0},x)& =& E^{\prime }\left[\phi \right({\omega }^{\prime },s,X_s^{0,x_0}\left({\omega }^{\prime }\right),x,u(s,X_s^{0,x_0}\left({\omega }^{\prime }\right)),u(s,x),\\ {\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{0,x_0}\left({\omega }^{\prime }\right)),{\hat{\sigma }}^{\ast }\cdot \mathrm{\nabla }u(s,x)\left)\right].\end{array}$$

Let $t=t_0<t_1<t_2<\cdots <t_n=T$ and $\lambda :=max\{t_{i+1}-t_i\}\to 0$. For each $t_i\in [t,T)$, applying Itô’s formula to $u(t_i,X_{t_i}^{t,x})$ and noticing that u satisfies Eq. (5.1), we get

The condition that $u\in C^{0,2}([0,T]\times {\mathbb{R}}^d;{\mathbb{R}}^n)$ and the continuity of f and g are adopted in the last equation.

Then we have

$$\begin{array}{rcl}u(t,x)-u(T,X_T^{t,x})& =& \sum _{i=0}^{n-1}[u(t_i,X_{t_i}^{t,x})-u(t_{i+1},X_{t_{i+1}}^{t,x})]\\ =& \sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}\hat{f}(s,X_s^{0,x_0},X_s^{t,x})ds+\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}\hat{g}(s,X_s^{0,x_0},X_s^{t,x})d{B}_s\\ -\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}{E}^{\prime }{\left[\sigma (s,{\left(X_s^{0,x_0}\right)}^{\prime },X_s^{t,x})\right]}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{t,x})d{W}_s\\ =& {\int }_t^T\hat{f}(s,X_s^{0,x_0},X_s^{t,x})ds+{\int }_t^T\hat{g}(s,X_s^{0,x_0},X_s^{t,x})d{B}_s\\ -{\int }_t^T{E}^{\prime }{\left[\sigma (s,{\left(X_s^{0,x_0}\right)}^{\prime },X_s^{t,x})\right]}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{t,x})d{W}_s.\end{array}$$

So, $Y_s^{t,x}:=u(s,X_s^{t,x})$, $Z_s^{t,x}:=E^{\prime }{[\sigma (s,{(X_s^{0,x_0})}^{\prime },X_s^{t,x})]}^{\ast }\cdot \mathrm{\nabla }u(s,X_s^{t,x})$ solves the mean-field BDSDE (4.3). The proof is now complete. □

Remark 5.1 Formula (5.2) generalizes the stochastic Feynman-Kac formula for SPDEs of the mean-field type.