- Research
- Open access
- Published:
Multiplicity results for nonlinear mixed boundary value problem
Boundary Value Problems volume 2012, Article number: 134 (2012)
Abstract
The aim of this paper is to establish multiplicity results of nontrivial and nonnegative solutions for mixed boundary value problems with the Sturm-Liouville equation. The approach is based on variational methods.
MSC: 34B15.
1 Introduction
The aim of this paper is to establish existence results of two and three nontrivial solutions for Sturm-Liouville problems with mixed conditions involving the ordinary p-Laplacian. We consider the following problem:
with , , with and . Here the nonlinearity is an -Carathéodory function and λ is a real positive parameter.
The existence of at least one solution for problem (P) has been obtained in [1], where only a unique algebraic condition on the nonlinear term is assumed (see [[1], Theorem 1.1]). In the present paper, first we obtain the existence of two solutions by combining an algebraic condition on f of type contained in [1] with the classical Ambrosetti-Rabinowitz condition.
(AR): There exist and such that
The role of (AR) is to ensure the boundness of the Palais-Smale sequences for the Euler-Lagrange functional associated to the problem. This is very crucial in the applications of critical point theory. Subsequently, an existence result of three positive solutions is obtained combining two algebraic conditions which guarantee the existence of two local minima for the Euler-Lagrange functional and applying the mountain pass theorem as given by Pucci and Serrin (see [2]) to ensure the existence of the third critical point.
Many mathematical models give rise to problems for which only nonnegative solutions make sense; therefore, many research articles on the theory of positive solutions have appeared. For a complete overview on this subject, we refer to the monograph [3].
In this paper, we also present, as a consequence of our main theorems, some results on the existence of nonnegative solutions for a particular problem of type
where is such that a.e. , , and is a nonnegative continuous function. In particular, we obtain for such a problem the existence of at least three nonnegative solutions by requiring that the function g has a superlinear behavior at zero, a sublinear behavior at infinity, and a particular growth in a suitable interval . By a similar approach, in [4], the authors obtain the existence of multiple solutions for a Neumann elliptic problem.
Multiplicity results for a mixed boundary value problem have been studied by several authors (see, for instance, [5–8] and references therein). In [5], the authors establish multiplicity results for problem (P), when , and, in particular, they obtain the existence of three solutions, one of which can be trivial. On the contrary, our results (Theorems 3.5 and 3.6) guarantee the existence of three nonnegative and nontrivial solutions.
In [7], by using a fixed point theorem, the existence of at least three solutions for a mixed boundary problem with the equation is obtained, by requiring, among other things, the boundness of f in a right neighborhood of zero (hypothesis (H6), Theorem 3.1), instead in our results (Theorems 3.5 and 3.6) the nonlinearity can blow up at zero.
Here, as an example, we present the following result which is a particular case of Theorem 3.6.
Theorem 1.1 Let be a nonnegative continuous function such that
and
Then, for each , the problem
admits at least three classical nonnegative and nontrivial solutions.
2 Preliminaries and basic notations
Our main tools are Theorems 2.1 and 2.2, consequences of the existence result of a local minimum [[9], Theorem 3.1] which is inspired by the Ricceri variational principle (see [10]). For more information on this topic see, for instance, [11] and [12].
Given a set X and two functionals , put


for all , with , and
for all .
Theorem 2.1 [[9], Theorem 5.1]
Let X be a reflexive real Banach space; be a sequentially weakly lower semicontinuous, coercive, and continuously Gâteaux differentiable function whose Gâteaux derivative admits a continuous inverse on ; be a continuously Gâteaux differentiable function whose Gâteaux derivative is compact. Put and assume that there are , , with , such that
where β and are given by (2.1) and (2.2).
Then, for each , there is such that for all and .
Theorem 2.2 [[9], Theorem 5.3]
Let X be a real Banach space; be a continuously Gâteaux differentiable function whose Gâteaux derivative admits a continuous inverse on ; be a continuously Gâteaux differentiable function whose Gâteaux derivative is compact. Fix and assume that
where ρ is given by (2.3), and for each , the function is coercive.
Then, for each , there is such that for all and .
Now, consider problem (P) and assume that with
Denote by endowed with the norm
Throughout the sequel, is an -Carathéodory function. We recall that a function is said to be an -Carathéodory function if is measurable for all , is continuous for almost every , and for all , one has . Clearly, if f is continuous in , then it is -Carathéodory.
Put
Moreover, it is well known that is compactly embedded in and one has
We use the following notations:
In order to study problem (P), we introduce the functionals defined as follows:
Clearly, the critical points of the functional on X are weak solutions of problem (P). We recall that is a weak solution of problem (P) if satisfies the following condition:
Clearly, if f is continuous, , and , the weak solutions for (P) are classical solutions.
3 Main results
In this section we present our main results.
Given two nonnegative constants c, d such that , where
put
Theorem 3.1 Under the following conditions:
-
(i)
there exist three constants , , d, with
(3.1)
such that
and ;
-
(ii)
there exist and such that
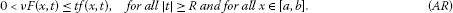
For each , problem (P) admits at least two nontrivial weak solutions , , with such that .
Proof The proof of this theorem is divided into two steps. In the first part, by applying Theorem 2.1, we prove the existence of a local minimum for the functional , where and are functionals given in (2.7) for all . Obviously, Φ and Ψ satisfy all regularity assumptions requested in Theorem 2.1, and the critical points in X of the functional are exactly the weak solutions of problem (P). To this end, we verify condition (2.4) of Theorem 2.1.
Define the following function , by setting
and estimate and as follows:
and
Fix , d, satisfying (3.1) and put and .
From (3.1), one has .
Moreover, for all such that , one has
Hence,
Now, arguing as before, we obtain
From hypothesis (i) and bearing in mind (3.3), (3.2), (3.5), and (3.6), we obtain
From Theorem 2.1, for each , admits at least one critical point which is a local minimum such that
Now, we prove the existence of the second local minimum distinct from the first one. To this end, we must show that the functional satisfies the hypotheses of the mountain pass theorem.
Clearly, the functional is of class and .
From the first part of the proof, we can assume that is a strict local minimum for in X. Therefore, there is such that , so condition [[13], (), Theorem 2.2] is verified.
Now, choosing any , from (ii) one has
as , so condition [[13], (), Theorem 2.2] is verified. Moreover, by standard computations, satisfies the Palais-Smale condition. Hence, the classical theorem of Ambrosetti and Rabinowitz ensures a critical point of such that . So, and are two distinct weak solutions of (P) and the proof is complete. □
Remark 3.1 We observe that in literature the existence of at least one nontrivial solution for differential problems is obtained associating to the classical Ambrosetti-Rabinowitz condition a hypothesis on the nonlinear term of type as . This implies that the problem possesses also the trivial solution . In Theorem 3.1, we find a nontrivial solution of the problem that actually is a proper local minimum of the Euler-Lagrange functional associated to the problem different from zero.
Now, we present an application of Theorem 2.2 which we will use to obtain multiple solutions.
Theorem 3.2 Assume that there exist two constants , , with , such that
and
Then, for each , where
problem (P) admits at least one nontrivial weak solution such that .
Proof The functionals Φ and Ψ satisfy all regularity assumptions requested in Theorem 2.2. Moreover, by standard computations, condition (3.8) implies that , , is coercive. So, our aim is to verify condition (2.5) of Theorem 2.2. To this end, put
Arguing as in the proof of Theorem 3.1, we obtain that
So, from our assumption, it follows that .
Hence, from Theorem 2.2 for each , the functional admits at least one local minimum such that and our conclusion is achieved. □
Remark 3.2 We point out that the same statement of above given result can be obtained by using a classical direct methods theorem (see [14]), but in addition we get the location of the solution, hence in particular the solution is nontrivial.
Now, we point out some results when the nonlinear term is with separable variables. To be precise, let
-
such that a.e. , , and
-
be a nonnegative continuous function,
consider the following boundary value problem:

We observe that the following results give the existence of multiple nonnegative solutions since the nonlinear term is supposed to be nonnegative. In order to justify what has been said above, we point out the following weak maximum principle.
Lemma 3.1 Suppose that is a weak solution of problem (P1), then is nonnegative.
Proof We claim that a weak solution is nonnegative. In fact, arguing by a contradiction and setting , one has . Put , one has (see, for instance, [[15], Lemma 7.6]). So, taking into account that is a weak solution and by choosing , one has
that is, which is absurd. Hence, our claim is proved. □
Corollary 3.1 Assume that
(i′) there exist three nonnegative constants , , d, with , such that
(ii′) there exist and such that
Then, for each , where
problem (P1) admits at least two nonnegative weak solutions and such that .
Theorem 3.3 Assume that there exist two positive constants c, d, with , such that
Further, suppose that there exist and such that
Then, for each , problem (P1) admits at least two nonnegative weak solutions.
Proof Our aim is to apply Corollary 3.1. To this end, we pick and . From (3.10), one has
On the other hand, one has
Hence, from Corollary 3.1 and taking (2.6) into account, the conclusion follows. □
A further consequence of Theorem 3.1 is the following result.
Theorem 3.4 Assume that
and there are constants and such that, for all , one has

Then, for each , where , problem (P1) admits at least two nonnegative weak solutions.
Proof Fix . Then there is such that . From (3.11), there is such that . Hence, Theorem 3.3 ensures the conclusion. □
Next, as a consequence of Theorems 3.3 and 3.2, the following theorem of the existence of three solutions is obtained.
Theorem 3.5 Assume that
Moreover, assume that there exist four positive constants c, d, , , with , such that (3.10),
and
are satisfied.
Then, for each , problem (P1) admits at least three weak nonnegative solutions.
Proof First, we observe that owing to (3.13). Next, fix . Theorem 3.3 ensures a nontrivial weak solution such that which is a local minimum for the associated functional , as well as Theorem 3.2 guarantees a nontrivial weak solution such that which is a local minimum for . Hence, the mountain pass theorem as given by Pucci and Serrin (see [2]) ensures the conclusion. □
Theorem 3.6 Assume that


Further, assume that there exist two positive constants , , with , such that
Then, for each , problem (P1) admits at least three weak nonnegative solutions.
Proof Clearly, (3.15) implies (3.8). Moreover, by choosing d small enough and , simple computations show that (3.14) implies (3.10). Finally, from (3.16) we get (3.7) and also (3.13). Hence, Theorem 3.5 ensures the conclusion. □
Finally, we present two examples of problems that admit multiple solutions owing to Theorems 3.4 and 3.6.
Example 3.1 Owing to Theorem 3.4, for each , the problem
admits at least two nonnegative solutions. In fact, one has and (AR) is satisfied as a simple computation shows. Moreover, one has .
Example 3.2 Consider the following problem:

It has three nonnegative solutions. In fact, let be a function defined as
Owing to Theorem 3.6, the following problem

admits three nonnegative classical solutions. In fact, one has
Moreover, taking into account that , by choosing and , one has and .
So, it is clear that any nonnegative solution u of problem () is also a solution of problem ().
References
D’Aguì G: Existence results for a mixed boundary value problem with Sturm-Liouville equation. Adv. Pure Appl. Math. 2011, 2: 237-248.
Pucci P, Serrin J: A mountain pass theorem. J. Differ. Equ. 1985, 63: 142-149.
Agarwal RV, O’Regan D, Wong PJY: Positive Solutions of Differential, Difference and Integral Equations. Kluwer Academic, Dordrecht; 1999.
Bonanno G, Sciammetta A: Existence and multiplicity results to Neumann problems for elliptic equations involving the p -Laplacian. J. Math. Anal. Appl. 2012, 390: 59-67. 10.1016/j.jmaa.2012.01.012
Averna, D, Giovannelli, N, Tornatore, E: Existence of three solutions for a mixed boundary value problem with the Sturm-Liouville equation. Preprint
Averna D, Salvati R: Three solutions for a mixed boundary value problem involving the one-dimensional p -Laplacian. J. Math. Anal. Appl. 2004, 298: 245-260. 10.1016/j.jmaa.2004.05.012
Lü H, O’Regan D, Zhong C: Multiple positive solutions for the one-dimensional singular p -Laplacian. Appl. Math. Comput. 2002, 133: 407-422. 10.1016/S0096-3003(01)00240-5
Salvati R: Multiple solutions for a mixed boundary value problem. Math. Sci. Res. J. 2003, 7: 275-283.
Bonanno G: A critical point theorem via the Ekeland variational principle. Nonlinear Anal. 2012, 75: 2992-3007. 10.1016/j.na.2011.12.003
Ricceri B: A general variational principle and some of its applications. J. Comput. Appl. Math. 2000, 113: 401-410. 10.1016/S0377-0427(99)00269-1
Bonanno G, Candito P: Non-differentiable functionals and applications to elliptic problems with discontinuous nonlinearities. J. Differ. Equ. 2008, 244: 3031-3059. 10.1016/j.jde.2008.02.025
Bonanno G, Marano SA: On the structure of the critical set of non-differentiable functions with a weak compactness condition. Appl. Anal. 2010, 89: 1-10. 10.1080/00036810903397438
Rabinowitz PH CBMS Reg. Conf. Ser. Math. 65. In Minimax Methods in Critical Point Theory with Applications to Differential Equations. Am. Math. Soc., Providence; 1986.
Struwe M: Variational Methods. Springer, Berlin; 1996.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order. 2nd edition. Springer, Berlin; 1983.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that she has no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
D’Aguì, G. Multiplicity results for nonlinear mixed boundary value problem. Bound Value Probl 2012, 134 (2012). https://doi.org/10.1186/1687-2770-2012-134
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-134