$H_{\lambda }$-regular vector functions and their boundary value problems

Abstract

Let $D=\left(\begin{array}{cc}\lambda +\frac{\partial }{\partial t}& 2\frac{\partial }{\partial \overline{z}}\\ 2\frac{\partial }{\partial z}& \lambda -\frac{\partial }{\partial t}\end{array}\right)$, where λ is a positive real constant. In this paper, by using the methods from quaternion calculus, we investigate the $H_{\lambda }$-regular vector functions, that is, the complex vector solutions $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ of the equation $D\mathrm{\Psi }=0$, and work out a systematic theory analogous to quaternionic regular functions. Differing from that, the component functions of quaternionic regular functions are harmonic, the component functions of $H_{\lambda }$-regular functions satisfy the modified Helmholtz equation, that is $({\lambda }^2-\mathrm{\Delta }){\psi }_i=0$, $i=1,2$. We give out a distribution solution of the inhomogeneous equation $Du=f$ and study some properties of the solution. Moreover, we discuss some boundary value problems for $H_{\lambda }$-regular functions and solutions of equation $Du=f$.

MSC:30G35, 35J05.

It is well known that the theories of holomorphic functions of one complex variable and regular functions of quaternion as well as Clifford calculus are closely connected with the theory of harmonic functions, i.e., their component functions are all harmonic. But side by side with the Laplace operator is the Helmholtz operator and modified Helmholtz operator

$${\mathrm{△}}_{\lambda }={\lambda }^2\pm △,\lambda (\in \mathbb{R})\ne 0,$$

which play an important role and are often met in application. In recent years, it has been considered that by replacing the harmonic function with the solutions of Helmholtz equation and modified Helmholtz equation, the theory of regular functions is naturally generalized in quaternion calculus and Clifford calculus. The theory has been well developed and has been applied to the research of some partial differential equations such as Helmholtz equation, Klein-Cordon equation, and Schroding equation. The corresponding results can be found in [1–3, 5–11, 13–15].

Let $\mathbb{H}(\mathbb{R})$ and $\mathbb{H}(\mathbb{C})$ denote the real and complex quaternion space respectively. Their basis elements 1, i, j, k satisfy the following relations: $i^2=j^2=k^2=-1$, $ij=-ji=k$, $jk=-kj=i$.

In [2, 3], the authors introduced a differential operator of first order $D_{\lambda }=\lambda +i\frac{\partial }{\partial x_1}+j\frac{\partial }{\partial x_2}+k\frac{\partial }{\partial x_3}$, where λ is a positive real constant. It is easy to see that

$$-D_{-\lambda }{D}_{\lambda }={\lambda }^2+\mathrm{\Delta },$$

where ${\lambda }^2+\mathrm{\Delta }$ is namely the 3-dimensional Helmholtz operator. A quaternion function theory associated with the operator was established which involved the Pompeiu formula corresponding to $D_{\lambda }$, the Cauchy integral formula for solutions of equation $D_{\lambda }u=0$, the Plemelj formula of Cauchy type integral and the theory of operator $T_{\lambda }$. By using these results, the authors investigated the Dirichlet boundary problems for Helmholtz equation

$$({\lambda }^2+\mathrm{\Delta })u=f.$$

Since the operator ${\lambda }^2-\mathrm{\Delta }$ can not be factorized into the product of two differential operators of first order in $\mathbb{H}(\mathbb{R})$, the quaternion function theory about modified Helmholtz equation was developed in complex quaternion space $\mathbb{H}(\mathbb{C})$, namely the operator ${\lambda }^2+\mathrm{\Delta }$, $\lambda \in \mathbb{C}$ and some related equations were directly investigated by $\mathbb{H}(\mathbb{C})$. However, different from $\mathbb{H}(\mathbb{R})$, $\mathbb{H}(\mathbb{C})$ is a Euclidean 8-space; and since there exists a set of zero divisors in $\mathbb{H}(\mathbb{C})$, a non-zero complex quaternion is not necessarily invertible. There exist many differences between the two theories.

In this article, we shall use the quasi-quaternion space introduced in [18, 19] and transform the modified Helmholtz operator into matric form $({\lambda }^2-\mathrm{△})e_0=D{D}^{\prime }$. By using the quaternion technique, we obtain a systematic theory about the $H_{\lambda }$-regular vector functions, that is, the complex vector solutions $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ of the equation $D\mathrm{\Psi }=0$, analogous to the quaternion regular function. Because the $H_{\lambda }$-regular vector functions are two-dimensional complex vector functions, this is more similar to the case of $\mathbb{H}(\mathbb{R})$.

For applications of partial differential equations, the research of boundary value problems is very important. How should appropriate boundary data be chosen for the Helmholtz equation or modified Helmholtz equation of first order? So far, there have been very few research works on the aspect. In this article, we introduce and investigate some Riemann-Hilbert type boundary value problems for $H_{\lambda }$-regular vector functions and solutions of the equation $Du=f$, obtain general solutions and solvable conditions respectively in different cases.

1 Some notations and definitions

Denote

$$e_0=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),e_1=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),e_2=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),e_3=\left(\begin{array}{cc}0& i\\ -i& 0\end{array}\right).$$

It is easy to see that

$$\begin{array}{c}{e}_1^2=e_2^2=e_3^2=e_0,e_1{e}_2=-e_2{e}_1=-i{e}_3,\hfill \\ e_2{e}_3=-e_3{e}_2=-i{e}_1,e_3{e}_1=-e_1{e}_3=-i{e}_2.\hfill \end{array}$$

Henceforth we shall abbreviate $e_0$ to 1.

Introduce the three-dimensional modified Helmholtz operator $D=\lambda +\mathrm{\nabla }$ of first order, where $\mathrm{\nabla }=\frac{\partial }{\partial t}{e}_1+\frac{\partial }{\partial x}{e}_2+\frac{\partial }{\partial y}{e}_3$, λ is a positive real constant. Define $D^{\prime }=\lambda -\mathrm{\nabla }$, then $D{D}^{\prime }=D^{\prime }D=({\lambda }^2-\mathrm{△})e_0$, where △ is the three-dimensional Laplace operator. The matrix forms of D, $D^{\prime }$ are

$$D=\left(\begin{array}{cc}\lambda +\frac{\partial }{\partial t}& 2\frac{\partial }{\partial \overline{z}}\\ 2\frac{\partial }{\partial z}& \lambda -\frac{\partial }{\partial t}\end{array}\right),D^{\prime }=\left(\begin{array}{cc}\lambda -\frac{\partial }{\partial t}& -2\frac{\partial }{\partial \overline{z}}\\ -2\frac{\partial }{\partial z}& \lambda +\frac{\partial }{\partial t}\end{array}\right),$$

where

$$\begin{array}{c}\frac{\partial }{\partial \overline{z}}=\frac{1}{2}(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}),\hfill \\ \frac{\partial }{\partial z}=\frac{1}{2}(\frac{\partial }{\partial x}-i\frac{\partial }{\partial y}),\hfill \end{array}$$

and then

$$D{D}^{\prime }=D^{\prime }D=\left(\begin{array}{cc}{\lambda }^2-\mathrm{\Delta }& 0\\ 0& {\lambda }^2-\mathrm{\Delta }\end{array}\right).$$

Let Ω be a region in $\mathbb{R}\times \mathbb{C}$ which identifies with ${\mathbb{R}}^3$. $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ is a complex vector function defined in Ω. If $\mathrm{\Psi }(t,z)\in C^1(\mathrm{\Omega })$ and satisfies the equation

$$D\mathrm{\Psi }=0,$$

(1)

then $\mathrm{\Psi }(t,z)$ will be called $H_{\lambda }$-regular vector function in Ω.

2 Pompeiu formula and Cauchy integral formula of $H_{\lambda }$-regular vector function

Let Ω be a bounded domain in $\mathbb{R}\times \mathbb{C}$ with piecewise smooth boundary S. $U(t,z)$, $V(t,z)$ are two-dimensional complex vector functions defined in Ω and $U(t,z),V(t,z)\in C^1(\mathrm{\Omega })\cap C(\overline{\mathrm{\Omega }})$. By the divergence theorem

$$\begin{array}{rcl}{\int }_{\mathrm{\Omega }}[(U\mathrm{\nabla })V+U(\mathrm{\nabla }V)]d\sigma & =& {\int }_{\mathrm{\Omega }}[\frac{\partial }{\partial x_1}(U{e}_{1}V)+\frac{\partial }{\partial x_2}(U{e}_{2}V)+\frac{\partial }{\partial x_3}(U{e}_{3}V)]d\sigma \\ =& {\int }_{S}U\mathrm{\Im }VdS,\end{array}$$

(2)

where $\mathrm{\Im }=e_{1}cos{\alpha }_1+e_{2}cos{\alpha }_2+e_{3}cos{\alpha }_3$, $(cos{\alpha }_1,cos{\alpha }_2,cos{\alpha }_3)$ denotes the unit outward normal to the surface S. From the equality (2), we have

$${\int }_{\mathrm{\Omega }}[U(DV)-\left(U{D}^{\prime }\right)V]d\sigma ={\int }_{S}U\mathrm{\Im }VdS.$$

(3)

It is easy to show that $\frac{1}{4\pi r}{e}^{-\lambda r}$, $r={(t^2+x^2+y^2)}^{\frac{1}{2}}$, is a fundamental solution of the modified Helmholtz operator ${\lambda }^2-\mathrm{\Delta }$. When $r\ne 0$, $({\lambda }^2-\mathrm{\Delta })(\frac{1}{4\pi r}{e}^{-\lambda r})=0$. We write

$$E(t,z)=D\left(\frac{1}{4\pi r}{e}^{-\lambda r}\right)=\frac{1}{4\pi }[\frac{\lambda }{r}-(\frac{\lambda }{r^2}+\frac{1}{r^3})(t{e}_1+x{e}_2+y{e}_3)]e^{-\lambda r}.$$

Suppose $u(t,z)$ is a complex vector function defined in Ω and $u(t,z)\in C^1(\mathrm{\Omega })\cap C(\overline{\mathrm{\Omega }})$. Let $p_0=(t_0,z_0)$ be a fixed point in Ω and $B_{\epsilon }(p_0)=\{|p-p_0|<\epsilon \}$ be an open ball whose center is $p_0$, and the radius ε is so small that $\overline{B_{\epsilon }(p_0)}\subset \mathrm{\Omega }$. Write ${\mathrm{\Omega }}_{\epsilon }=\mathrm{\Omega }\setminus \overline{B_{\epsilon }(p_0)}$. Using the formula (3) in ${\mathrm{\Omega }}_{\epsilon }$ and replacing U, V by $E(p-p_0)$, $u(p)$ respectively, we have

$${\int }_{{\mathrm{\Omega }}_{\epsilon }}E(p-p_0)Dud\sigma ={\int }_{S}E(p-p_0)\mathrm{\Im }u(p)dS-{\int }_{\partial B_{\epsilon }(p_0)}E(p-p_0)\mathrm{\Im }u(p)dS.$$

(4)

Where

$$\begin{array}{c}{\int }_{\partial B_{\epsilon }(p_0)}E(p-p_0)\mathrm{\Im }u(p)dS=I_1+I_2+I_3,\hfill \\ I_1=\frac{\lambda e^{-\lambda \epsilon }}{4\pi {\epsilon }^2}{\int }_{\partial B_{\epsilon }(p_0)}[(t-t_0)e_1+(x-x_0)e_2+(y-y_0)e_3]u(p)dS,\hfill \\ I_2=-\frac{\lambda e^{-\lambda \epsilon }}{4\pi \epsilon }{\int }_{\partial B_{\epsilon }(p_0)}u(p)dS,\hfill \\ I_3=-\frac{e^{-\lambda \epsilon }}{4\pi {\epsilon }^2}{\int }_{\partial B_{\epsilon }(p_0)}u(p)dS.\hfill \end{array}$$

It is easy to show that

$$\underset{\epsilon \to 0}{lim}{I}_1=0,\underset{\epsilon \to 0}{lim}{I}_2=0,\underset{\epsilon \to 0}{lim}{I}_3=-u(p_0).$$

Then letting ε tend to zero in (4), we obtain the following Pompeiu formula corresponding to the operator D.

Theorem 1 Let Ω be a bounded domain in $\mathbb{R}\times \mathbb{C}$ with piecewise smooth boundary S. If $u(t,z)=u(p)$ is a complex vector function defined in Ω and $u(t,z)\in C^1(\mathrm{\Omega })\cap C(\overline{\mathrm{\Omega }})$, then

$$u(t,z)=-{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }u\left(p^{\prime }\right)d{S}_{p^{\prime }}+{\int }_{\mathrm{\Omega }}E(p^{\prime }-p)D_{p^{\prime }}ud{\sigma }_{p^{\prime }},(t,z)\in \mathrm{\Omega }.$$

(5)

By applying Theorem 1, we can deduce the following Cauchy integral formula of the $H_{\lambda }$-regular vector function.

Theorem 2 If a complex vector function $\mathrm{\Psi }(t,z)\in C^1(\mathrm{\Omega })\cap C(\overline{\mathrm{\Omega }})$ and satisfies the equation $D\mathrm{\Psi }=0$ in Ω, then

$$\mathrm{\Psi }(t,z)=-{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }u\left(p^{\prime }\right)d{S}_{p^{\prime }},(t,z)\in \mathrm{\Omega },$$

(6)

and if $(t,z)\overline{\in }\mathrm{\Omega }$, then

$${\int }_{S}E(p^{\prime }-p)\mathrm{\Im }u\left(p^{\prime }\right)d{S}_{p^{\prime }}=0.$$

(7)

Proof The formula (6) follows directly from the Pompeiu formula (5) and the equality (7) can easily be derived from (3). □

3 Cauchy type integral and Plemelj formula

Let $\phi (t,z)$ be a complex vector function defined on a closed smooth surface S in $\mathbb{R}\times \mathbb{C}$, $\phi (t,z)\in C_{\alpha }(S)$, $0<\alpha <1$. Denote

$$\mathrm{\Psi }(t,z)=-{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }},$$

(8)

and call $\mathrm{\Phi }(t,z)$ the Cauchy type integral with respect to the operator D. In the following, we shall simply call it the Cauchy type integral. In addition, $\phi (t,z)$ is called the density function of $\mathrm{\Psi }(t,z)$.

For arbitrary $p=(t,z)\overline{\in }S$, there exists a neighborhood $B_{\rho }(p)$ of p which does not intersect with S. In $B_{\rho }(p)$,

$$\begin{array}{rcl}D\mathrm{\Psi }(t,z)& =& -(\lambda +{\mathrm{\nabla }}_p){\int }_S(\lambda +{\mathrm{\nabla }}_{p^{\prime }})\left(\frac{1}{4\pi |p^{\prime }-p|}{e}^{-\lambda |p^{\prime }-p|}\right)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}\\ =& -(\lambda +{\mathrm{\nabla }}_p){\int }_S(\lambda -{\mathrm{\nabla }}_p)\left(\frac{1}{4\pi |p^{\prime }-p|}{e}^{-\lambda |p^{\prime }-p|}\right)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}\\ =& -{\int }_S({\lambda }^2-{\mathrm{△}}_p)\left(\frac{1}{4\pi |p^{\prime }-p|}{e}^{-\lambda |p^{\prime }-p|}\right)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}=0.\end{array}$$

Consequently, $\mathrm{\Psi }(t,z)$ is $H_{\lambda }$-regular in the exterior of S. In addition, it is easy to see that $\mathrm{\Psi }(t,z)$ converges to 0 as $(t,z)\to \mathrm{\infty }$.

When $(t,z)\in S$, we provide that the integral on the right-hand side of (8) represents Cauchy’s principal value.

Lemma 1 Let Ω be a bounded domain in $\mathbb{R}\times \mathbb{C}$ with smooth boundary S. If $p\in S$, in the sense of Cauchy’s principal value, then

$${\int }_{S}E(p^{\prime }-p)\mathrm{\Im }d{S}_{p^{\prime }}=-\frac{1}{2}{e}_0+\lambda {\int }_{\mathrm{\Omega }}E(p^{\prime }-p)d{\sigma }_{p^{\prime }}.$$

(9)

Proof Let $B_{\epsilon }(p)$ be an open ball with the radius ε and the center p, write the component of $\partial B_{\epsilon }(p)$ lying in the exterior of Ω as Γ. Then x is an interior point of the region inclosed by the closed surface $S^{\prime }=(S\setminus (S\cap B_{\epsilon }(p)))\cup \mathrm{\Gamma }$. By the Pompeiu formula (5), we have

$$e_0=-({\int }_{S\setminus (S\cap B_{\epsilon }(p))}+{\int }_{\mathrm{\Gamma }})E(p^{\prime }-p)\mathrm{\Im }d{S}_{p^{\prime }}+\lambda {\int }_{\mathrm{\Omega }\cup B_{\epsilon }(p)}E(p^{\prime }-p)d{\sigma }_{p^{\prime }}.$$

(10)

Similarly to the proof of Theorem 1, we can derive

$$\underset{\epsilon \to 0}{lim}{\int }_{\mathrm{\Gamma }}E(p^{\prime }-p)\mathrm{\Im }d{S}_{p^{\prime }}=-\frac{1}{2}{e}_0.$$

Letting $\epsilon \to 0$ in (10), it follows that (9) holds. □

By using Lemma 1, we can obtain the following Plemelj formula of the Cauchy type integral (8).

Theorem 3 Write the domain Ω as ${\mathrm{\Omega }}^{+}$ and the complementary domain of $\overline{\mathrm{\Omega }}$ as ${\mathrm{\Omega }}^{-}$. When p tends to $p_0(\in S)$ from ${\mathrm{\Omega }}^{+}$ and ${\mathrm{\Omega }}^{-}$ respectively, the limits of the Cauchy type integral (8) exist, which will be written as ${\mathrm{\Psi }}^{+}(p_0)$ and ${\mathrm{\Psi }}^{-}(p_0)$ respectively, and

$$\{\begin{array}{c}{\mathrm{\Psi }}^{+}(p_0)=-{\int }_{S}E(p-p_0)\mathrm{\Im }\phi (p)d{S}_p+\frac{1}{2}\phi (p_0),\hfill \\ {\mathrm{\Psi }}^{-}(p_0)=-{\int }_{S}E(p-p_0)\mathrm{\Im }\phi (p)d{S}_p-\frac{1}{2}\phi (p_0).\hfill \end{array}$$

(11)

The above formula can be rewritten as

$$\{\begin{array}{c}{\mathrm{\Psi }}^{+}(p_0)-{\mathrm{\Psi }}^{-}(p_0)=\phi (p_0),\hfill \\ {\mathrm{\Psi }}^{+}(p_0)+{\mathrm{\Psi }}^{-}(p_0)=-2{\int }_{S}E(p-p_0)\mathrm{\Im }\phi (p)d{S}_p.\hfill \end{array}$$

(12)

Proof Since $\phi (p)\in C_{\alpha }(S)$, $0<\alpha <1$, therefore the improper integral ${\int }_{S}E(p-p_0)\mathrm{\Im }(\phi (p)-\phi (p_0))d{S}_p$ is convergent. By Lemma 1, we have

$$\begin{array}{rcl}{\int }_{S}E(p-p_0)\mathrm{\Im }\phi (p)d{S}_p& =& {\int }_{S}E(p-p_0)\mathrm{\Im }(\phi (p)-\phi (p_0))d{S}_p\\ -\frac{1}{2}\phi (p_0)+\lambda {\int }_{\mathrm{\Omega }}E(p-p_0)d{\sigma }_y\cdot \phi (x_0).\end{array}$$

The Cauchy type integral (8) can be written in the following form:

$$\begin{array}{rcl}-{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}& =& -{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }(\phi \left(p^{\prime }\right)-\phi (p_0))d{S}_{p^{\prime }}\\ -{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }d{S}_{p^{\prime }}\cdot \phi (p_0).\end{array}$$

(13)

By the Pompeiu formula, we obtain

$${\int }_{S}E(p^{\prime }-p)\mathrm{\Im }d{S}_{p^{\prime }}=\{\begin{array}{c}-e_0+\lambda {\int }_{\mathrm{\Omega }}E(p^{\prime }-p)d{\sigma }_{p^{\prime }},p\in {\mathrm{\Omega }}^{+},\hfill \\ \lambda {\int }_{\mathrm{\Omega }}E(p^{\prime }-p)d{\sigma }_{p^{\prime }},p\in {\mathrm{\Omega }}^{-}.\hfill \end{array}$$

When $p(\overline{\in }S)\to p_0(\in S)$, using the method similar to one complex variable [12, 13], we can show that

$$\underset{p\to p_0}{lim}{\int }_{S}E(p^{\prime }-p)\mathrm{\Im }(\phi \left(p^{\prime }\right)-\phi (p_0))d{S}_{p^{\prime }}={\int }_{S}E(p^{\prime }-p_0)\mathrm{\Im }(\phi \left(p^{\prime }\right)-\phi (p_0))d{S}_{p^{\prime }}.$$

Moreover, by using the Hölder inequality, it is easy to show that

$$\underset{p\to p_0}{lim}{\int }_{\mathrm{\Omega }}E(p^{\prime }-p)d{\sigma }_{p^{\prime }}={\int }_{\mathrm{\Omega }}E(p^{\prime }-p_0)d{\sigma }_{p^{\prime }}.$$

Thus letting p tend to $p_0(\in S)$ from ${\mathrm{\Omega }}^{+}$ and ${\mathrm{\Omega }}^{-}$ respectively in (13), we get

$$\begin{array}{c}{\mathrm{\Psi }}^{+}(p_0)=-{\int }_{S}E(p^{\prime }-p_0)\mathrm{\Im }(\phi \left(p^{\prime }\right)-\phi (p_0))d{S}_{p^{\prime }}+\phi (p_0)-\lambda {\int }_{\mathrm{\Omega }}E(p^{\prime }-p_0)d{\sigma }_{p^{\prime }}\cdot \phi (p_0)\hfill \\ \phantom{{\mathrm{\Psi }}^{+}(p_0)}=-{\int }_{S}E(p^{\prime }-p_0)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}+\frac{1}{2}\phi (p_0),\hfill \\ {\mathrm{\Psi }}^{-}(p_0)=-{\int }_{S}E(p^{\prime }-p_0)\mathrm{\Im }(\phi \left(p^{\prime }\right)-\phi (p_0))d{S}_{p^{\prime }}-\lambda {\int }_{\mathrm{\Omega }}E(p^{\prime }-p_0)d{\sigma }_{p^{\prime }}\cdot \phi (p_0)\hfill \\ \phantom{{\mathrm{\Psi }}^{-}(p_0)}=-{\int }_{S}E(p^{\prime }-p_0)\mathrm{\Im }\phi \left(p^{\prime }\right)d{S}_{p^{\prime }}-\frac{1}{2}\phi (p_0).\hfill \end{array}$$

This is (11), and (12) is easily deduced from (11). □

The following result follows directly from Theorem 3.

Corollary 1 Let Ω be a bounded domain in $\mathbb{R}\times \mathbb{C}$ whose boundary is a closed smooth surface S. $\phi (t,z)$ is a complex vector function defined on the surface S, and $\phi (t,z)\in C_{\alpha }(S)$, $0<\alpha <1$. Then the Cauchy type integral (8) whose density function is $\phi (t,z)$ is a Cauchy integral if and only if $(t_0,z_0)\in S$,

$${\mathrm{\Psi }}^{-}(t_0,z_0)=0.$$

4 Operator $T_{\mathrm{\Omega }}f$

Let $f(t,z)$ be a complex vector function defined in a bounded domain Ω of $\mathbb{R}\times \mathbb{C}$. Denote

$$T_{\mathrm{\Omega }}f={\int }_{\mathrm{\Omega }}E(p^{\prime }-p)f\left(p^{\prime }\right)d{\sigma }_{p^{\prime }},$$

(14)

where

$$\begin{array}{rcl}E(p^{\prime }-p)& =& \frac{1}{4\pi }[\frac{\lambda }{|p^{\prime }-p|}\\ -(\frac{\lambda }{{|p^{\prime }-p|}^2}+\frac{1}{{|p^{\prime }-p|}^3})((t^{\prime }-t)e_1+(x^{\prime }-x)e_2+(y^{\prime }-y)e_3)]e^{-\lambda |p^{\prime }-p|}.\end{array}$$

In this section, we shall get that if $f(t,z)\in L_1(\overline{\mathrm{\Omega }})$, then $T_{\mathrm{\Omega }}f$ is a distribution solution of the inhomogeneous equation

$$Du=f,$$

(15)

and shall discuss some properties of the operator $T_{\mathrm{\Omega }}f$.

Similarly to the quaternion calculus [3, 17], we can obtain the following results.

Theorem 4 If $f(t,z)\in L_1(\overline{\mathrm{\Omega }})$, then $T_{\mathrm{\Omega }}f$ exists for all $(t,z)$ in the exterior of Ω. Beside $T_{\mathrm{\Omega }}f$ is $H_{\lambda }$-regular in the exterior of Ω and

$$T_{\mathrm{\Omega }}f=0,(t,z)\to \mathrm{\infty }.$$

Theorem 5 Let $f(t,z)\in L_1(\overline{\mathrm{\Omega }})$, then $T_{\mathrm{\Omega }}f$ exists almost everywhere on $\mathbb{R}\times \mathbb{C}$ and belongs to $L_p({\overline{\mathrm{\Omega }}}_{\ast })$, $1\le p<\frac{3}{2}$, where ${\mathrm{\Omega }}_{\ast }$ denotes any bounded domain in $\mathbb{R}\times \mathbb{C}$.

For complex vector functions $f(t,z)=\left(\begin{array}{c}{f}_1(t,z)\\ f_2(t,z)\end{array}\right)$, $\phi (x)=\left(\begin{array}{c}{\phi }_1(t,z)\\ {\phi }_2(t,z)\end{array}\right)$ given on Ω, define

$$(f,\phi )={\int }_{\mathrm{\Omega }}(\overline{f_1}{\phi }_1+\overline{f_2}{\phi }_2)d\sigma .$$

When $f(t,z)\in L_1(\overline{\mathrm{\Omega }})$, $\phi (t,z)\in C_0^{\mathrm{\infty }}(\mathrm{\Omega })$, it is easy to show that $f(\phi )=(f,\phi )$ is a distribution on $C_0^{\mathrm{\infty }}(\mathrm{\Omega })$.

Theorem 6 Let $f(t,z)\in L_1(\overline{\mathrm{\Omega }})$. Then for any $\phi (t,z)=\left(\begin{array}{c}{\phi }_1(t,z)\\ {\phi }_2(t,z)\end{array}\right)\in C_0^{\mathrm{\infty }}(\mathrm{\Omega })$,

$$(T_{\mathrm{\Omega }}f,D^{\prime }\phi )=(f,\phi )$$

holds.

Proof From the equality (2), we get

$${\int }_{\mathrm{\Omega }}[U\left(D^{\prime }V\right)-(UD)V]d\sigma =-{\int }_{S}U\mathrm{\Im }VdS.$$

In the above equality replacing U, V by $E^{\prime }(p^{\prime }-p)=D^{\prime }(\frac{1}{4\pi |p^{\prime }-p|}{e}^{-\lambda |p^{\prime }-p|})$, $u(p)$ respectively, by using the method analogous to the proof of Pompeiu formula (5), we can derive the Pompeiu formula corresponding to the operator $D^{\prime }$, i.e., if $u(t,z)\in C^1(\mathrm{\Omega })\cap C(\overline{\mathrm{\Omega }})$, then

$$u(t,z)={\int }_S{E}^{\prime }(p^{\prime }-p)\mathrm{\Im }u\left(p^{\prime }\right)d{S}_{p^{\prime }}+{\int }_{\mathrm{\Omega }}{E}^{\prime }(p^{\prime }-p)D_{p^{\prime }}^{\prime }ud{\sigma }_{p^{\prime }},(t,z)\in \mathrm{\Omega }.$$

(16)

Thus for any $\phi (t,z)\in C_0^{\mathrm{\infty }}(\mathrm{\Omega })$,

$$\phi (t,z)=T_{\mathrm{\Omega }}^{\prime }{D}^{\prime }\phi ={\int }_{\mathrm{\Omega }}{E}^{\prime }(p^{\prime }-p)D_{p^{\prime }}^{\prime }\phi d{\sigma }_{p^{\prime }}$$

holds.

In accordance with Theorem 5, $T_{\mathrm{\Omega }}f\in L_1(\overline{\mathrm{\Omega }})$. Thereby by the Fubini theorem,

$$(T_{\mathrm{\Omega }}f,D^{\prime }\phi )=(f,T_{\mathrm{\Omega }}^{\prime }\left(D^{\prime }\phi \right))=(f,\phi ),$$

the desired result follows. □

Let complex vector functions $f,g\in L_1(\overline{\mathrm{\Omega }})$. If for any $\phi (t,z)\in C_0^{\mathrm{\infty }}(\mathrm{\Omega })$,

$$(g,D^{\prime }\phi )=(f,\phi ),$$

then f is called a generalized derivative corresponding to the operator D of g. The derivative is denoted by $f={(g)}_D$. From Theorem 6 and the definition, ${(T_{\mathrm{\Omega }}f)}_D=f$.

Theorem 7 If a complex vector function $g\in C^1(\mathrm{\Omega })$ and satisfies the equation $Dg=f$, then

$${(g)}_D=f.$$

This shows that if the complex vector function g is a classical solution of the equation (15), then it is also a distributional solution of the equation.

Proof It follows by the definition and the divergence theorem. □

Let $a=(a_1,a_2)$ be a complex vector. The model of a is defined

$$|a|={({|a_1|}^2+{|a_2|}^2)}^{\frac{1}{2}}.$$

It is easy to show that

$$\begin{array}{rcl}|a(t{e}_1+x{e}_2+y{e}_3)|& =& |(a_1,a_2)\left(\begin{array}{cc}t& z\\ \overline{z}& -t\end{array}\right)|=|(a_{1}t+a_2\overline{z},a_{1}z-a_{2}t)|\\ =& {\left[({|a_1|}^2+{|a_2|}^2)(t^2+{|z|}^2)\right]}^{\frac{1}{2}}=|a||t{e}_1+x{e}_2+y{e}_3|.\end{array}$$

By using similar methods to those used when proving the Hölder continuous of the operator T in quaternion calculus [16, 17], we can prove the following theorem.

Theorem 8 Let Ω be a bounded domain in $\mathbb{R}\times \mathbb{C}$, the complex vector function $f(t,z)\in L_p(\overline{\mathrm{\Omega }})$, $p>3$.

• (a) For any $\zeta \in \mathbb{R}\times \mathbb{C}$,

  $$|T_{\mathrm{\Omega }}f(\zeta )|\le M(p,\mathrm{\Omega }){\parallel f\parallel }_{L_p},$$

  (17)

where $M(p,\mathrm{\Omega })$ is a positive real constant depending only on p, Ω.

• (b) $g(\zeta )=T_{\mathrm{\Omega }}f(\zeta )$ satisfies

  $$|g({\zeta }_1)-g({\zeta }_2)|\le M^{\prime }(p){\parallel f\parallel }_{L_p}{|{\zeta }_1-{\zeta }_2|}^{\alpha },\alpha =\frac{p-3}{p},{\zeta }_1,{\zeta }_2\in \mathbb{R}\times \mathbb{C},$$

  (18)

where $M(p)$ is a positive real constant depending only on p.

The inequalities (17) and (18) imply that $T_{\mathrm{\Omega }}f$ is a compact mapping from $L_p(\overline{\mathrm{\Omega }})$, $p>3$ into $C_{\alpha }(\overline{\mathrm{\Omega }})$, $\alpha =\frac{p-3}{p}$, and

$${\parallel T_{\mathrm{\Omega }}f\parallel }_{C_{\alpha }(\overline{\mathrm{\Omega }})}\le M{\parallel f\parallel }_{L_p},p>3,\alpha =\frac{p-3}{p}.$$

(19)

Proof (a) From the definition (14) of $T_{\mathrm{\Omega }}f$,

$$|T_{\mathrm{\Omega }}f|\le \frac{\lambda }{2\pi }{\int }_{\mathrm{\Omega }}\frac{e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{|{\zeta }^{\prime }-\zeta |}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}+\frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\frac{e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{{|{\zeta }^{\prime }-\zeta |}^2}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}=I_1+I_2.$$

Since

$$e^{-\lambda |{\zeta }^{\prime }-\zeta |}\le \frac{1}{\lambda |{\zeta }^{\prime }-\zeta |},$$

we have by Hölder’s inequality

$$I_1\le \frac{1}{2\pi }{\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}{\parallel f\parallel }_{L_p},$$

where $\frac{1}{p}+\frac{1}{q}=1$. By hypothesis $p>3$, we have $q<\frac{3}{2}$. Let $d={sup}_{\zeta ,{\zeta }^{\prime }\in \overline{\mathrm{\Omega }}}|\zeta -{\zeta }^{\prime }|$, $d_1=dist(\zeta ,\overline{\mathrm{\Omega }})$, namely d, $d_1$ denote the diameter of a bounded domain Ω and the distance between ζ and $\overline{\mathrm{\Omega }}$ respectively.

If $\zeta \in \overline{\mathrm{\Omega }}$,

$${\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}\le {\left({\int }_{|{\zeta }^{\prime }-\zeta |\le d}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}={\left(\frac{4\pi d^{3-2q}}{3-2q}\right)}^{\frac{1}{q}}.$$

If $\zeta \overline{\in }\overline{\mathrm{\Omega }}$,

$$\begin{array}{rcl}{\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}& \le & {\left({\int }_{d_1\le |{\zeta }^{\prime }-\zeta |\le d_1+d}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}\\ =& {\left(\frac{4\pi d^{3-2q}}{3-2q}\right)}^{\frac{1}{q}}{[{(1+\frac{d_1}{d})}^{3-2q}-{\left(\frac{d_1}{d}\right)}^{3-2q}]}^{\frac{1}{q}}\\ \le & {\left(\frac{4\pi d^{3-2q}}{3-2q}\right)}^{\frac{1}{q}}.\end{array}$$

The last inequality is immediate from

$$0<{(1+\frac{d_1}{d})}^{3-2q}-{\left(\frac{d_1}{d}\right)}^{3-2q}\le 1.$$

In fact, from $0<\beta =3-2q<1$, it is easy to see that the real function $\mu (x)={(1+x)}^{\beta }-x^{\beta }$ is a monotone decreasing function in $[0,+\mathrm{\infty })$ and $\mu (0)=0$, so that $0<\mu (x)\le 1$.

Let

$$M_1(p,\mathrm{\Omega })=\frac{1}{2\pi }{\left(\frac{4\pi d^{3-2q}}{3-2q}\right)}^{\frac{1}{q}}.$$

Hence we obtain

$$I_1\le M_1(p,\mathrm{\Omega }){\parallel f\parallel }_{L_p}.$$

(20)

Noting

$$e^{-\lambda |{\zeta }^{\prime }-\zeta |}\le 1,$$

thus

$$\begin{array}{rcl}{I}_2& =& \frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\frac{e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{{|{\zeta }^{\prime }-\zeta |}^2}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}\\ \le & \frac{1}{4\pi }{\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-\zeta |}^{2q}}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}{\parallel f\parallel }_{L_p}\le \frac{1}{4\pi }{\left(\frac{4\pi d^{3-2q}}{3-2q}\right)}^{\frac{1}{q}}{\parallel f\parallel }_{L_p},\end{array}$$

i.e.,

$$I_2\le \frac{1}{2}{M}_1(p,\mathrm{\Omega }){\parallel f\parallel }_{L_p}.$$

(21)

The inequality (17) follows immediately from (20) and (21).

• (b) Without loss of generality, we may take $|{\zeta }_1-{\zeta }_2|<1$. We write

  $$\begin{array}{rcl}g(\zeta )& =& \frac{\lambda }{4\pi }{\int }_{\mathrm{\Omega }}\frac{e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{|{\zeta }^{\prime }-\zeta |}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}-\frac{\lambda }{4\pi }{\int }_{\mathrm{\Omega }}\frac{({\zeta }^{\prime }-\zeta )e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{{|{\zeta }^{\prime }-\zeta |}^2}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}\\ -\frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\frac{({\zeta }^{\prime }-\zeta )e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{{|{\zeta }^{\prime }-\zeta |}^3}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}\\ =& g_1(\zeta )-g_2(\zeta )-g_3(\zeta ),\end{array}$$

where

$${\zeta }^{\prime }-\zeta =(t^{\prime }-t)e_1+(x^{\prime }-x)e_2+(y^{\prime }-y)e_3.$$

It is easy to see that ${({\zeta }^{\prime }-\zeta )}^2={|{\zeta }^{\prime }-\zeta |}^2$.

We have

$$\begin{array}{c}|g_1({\zeta }_1)-g_1({\zeta }_2)|\hfill \\ =\frac{\lambda }{4\pi }\left|{\int }_{\mathrm{\Omega }}\frac{(|{\zeta }^{\prime }-{\zeta }_2|-|{\zeta }^{\prime }-{\zeta }_1|)e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}+|{\zeta }^{\prime }-{\zeta }_1|(e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}-e^{-\lambda |{\zeta }^{\prime }-{\zeta }_2|})}{|{\zeta }^{\prime }-{\zeta }_1||{\zeta }^{\prime }-{\zeta }_2|}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}\right|\hfill \\ \le \frac{\lambda }{4\pi }{\int }_{\mathrm{\Omega }}\frac{|{\zeta }_1-{\zeta }_2|(1+\lambda |{\zeta }^{\prime }-{\zeta }_1|)}{|{\zeta }^{\prime }-{\zeta }_1||{\zeta }^{\prime }-{\zeta }_2|}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}.\hfill \end{array}$$

Here we use the estimates

$$e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}\le 1$$

and

$$|e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}-e^{-\lambda |{\zeta }^{\prime }-{\zeta }_2|}|\le \lambda ||{\zeta }^{\prime }-{\zeta }_2|-|{\zeta }^{\prime }-{\zeta }_1||\le \lambda |{\zeta }_1-{\zeta }_2|.$$

We get by Hölder’s inequality

$${\int }_{\mathrm{\Omega }}\frac{1}{|{\zeta }^{\prime }-{\zeta }_1||{\zeta }^{\prime }-{\zeta }_2|}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}\le {\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-{\zeta }_1|}^q{|{\zeta }^{\prime }-{\zeta }_2|}^q}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}{\parallel f\parallel }_{L_p},$$

and

$${\int }_{\mathrm{\Omega }}\frac{1}{|{\zeta }^{\prime }-{\zeta }_2|}\left|f\left({\zeta }^{\prime }\right)\right|d{\sigma }_{{\zeta }^{\prime }}\le {\left({\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-{\zeta }_2|}^q}d{\sigma }_{{\zeta }^{\prime }}\right)}^{\frac{1}{q}}{\parallel f\parallel }_{L_p}.$$

Using the inequality

$${\int }_{\mathrm{\Omega }}\frac{1}{{|{\zeta }^{\prime }-{\zeta }_1|}^{\alpha }{|{\zeta }^{\prime }-{\zeta }_2|}^{\beta }}d{\sigma }_{{\zeta }^{\prime }}\le \{\begin{array}{cc}{c}_1{|{\zeta }_1-{\zeta }_2|}^{3-\alpha -\beta },\hfill & 0<\alpha ,\beta <3,\alpha +\beta >3,\hfill \\ c_2,\hfill & 0\le \alpha ,\beta <3,\alpha +\beta <3,\hfill \end{array}$$

where $c_1$, $c_2$ are positive real constants, and noting $q<\frac{3}{2}$, we then obtain

$$|g_1({\zeta }_1)-g_1({\zeta }_2)|\le M_1^{\prime }(p){\parallel f\parallel }_{L_p}|{\zeta }_1-{\zeta }_2|.$$

(22)

By simple computation we have

$$|g_2({\zeta }_1)-g_2({\zeta }_2)|=\frac{\lambda }{4\pi }\left|{\int }_{\mathrm{\Omega }}\frac{({\zeta }_1-{\zeta }_2)e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}+({\zeta }^{\prime }-{\zeta }_1)(e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}-e^{-\lambda |{\zeta }^{\prime }-{\zeta }_2|})}{({\zeta }^{\prime }-{\zeta }_1)({\zeta }^{\prime }-{\zeta }_2)}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}\right|,$$

and

$$\begin{array}{rcl}|g_3({\zeta }_1)-g_3({\zeta }_2)|& =& \frac{1}{4\pi }\left|{\int }_{\mathrm{\Omega }}\right\{\frac{[|{\zeta }^{\prime }-{\zeta }_2|({\zeta }_1-{\zeta }_2)+({\zeta }^{\prime }-{\zeta }_1)(|{\zeta }^{\prime }-{\zeta }_2|-|{\zeta }^{\prime }-{\zeta }_1|)]e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}}{|{\zeta }^{\prime }-{\zeta }_1||{\zeta }^{\prime }-{\zeta }_2|({\zeta }^{\prime }-{\zeta }_1)({\zeta }^{\prime }-{\zeta }_2)}\\ +\frac{({\zeta }^{\prime }-{\zeta }_1)(e^{-\lambda |{\zeta }^{\prime }-{\zeta }_1|}-e^{-\lambda |{\zeta }^{\prime }-{\zeta }_2|})}{|{\zeta }^{\prime }-{\zeta }_2|({\zeta }^{\prime }-{\zeta }_1)({\zeta }^{\prime }-{\zeta }_2)}\left\}f\left({\zeta }^{\prime }\right)d{\sigma }_{{\zeta }^{\prime }}\right|.\end{array}$$

By using a similar method, we can obtain

$$|g_2({\zeta }_1)-g_2({\zeta }_2)|\le M_2^{\prime }(p){\parallel f\parallel }_{L_p}|{\zeta }_1-{\zeta }_2|$$

(23)

and

$$|g_3({\zeta }_1)-g_3({\zeta }_2)|\le M_3^{\prime }(p){\parallel f\parallel }_{L_p}{|{\zeta }_1-{\zeta }_2|}^{\alpha }.$$

(24)

The required estimate then follows by combining the resulting inequalities. □

5 Some boundary value problems for $H_{\lambda }$-regular functions

It is well known that the Dirichlet problem for analytic functions $w(z)$ in a bounded domain of the complex plane, boundary value of which is a given complex value function, is overdetermined, thereby being unsolvable in general. In the theory of boundary value problems for analytic functions, the boundary condition is replaced by $Rew=r(t)$, and a more general problem is the so-called Riemann-Hilbert problem with boundary condition $Re\overline{\lambda (t)}w=r(t)$. Analogously to this, the Dirichlet problem for $H_{\lambda }$-regular functions, boundary value of which is a given complex value vector function, is also overdetermined, and we have therefore to consider new boundary conditions. In this section, we introduce and discuss some Riemann-Hilbert type boundary value problems for $H_{\lambda }$-regular vector functions.

Let Ω be a bounded domain with smooth boundary S in $\mathbb{R}\times \mathbb{C}$, $0\in \mathrm{\Omega }$. S satisfies the exterior sphere condition, that is, for every point $\zeta \in S$, there exists a ball B satisfying $\overline{B}\cap \overline{\mathrm{\Omega }}=\zeta$. ${\mathrm{\Omega }}_0$ denotes the transversal domain of Ω on the plane $t=0$, its boundary $L=\partial {\mathrm{\Omega }}_0$ is a closed smooth curve and the projection of every point of Ω on the plane $t=0$ is in ${\mathrm{\Omega }}_0$. We consider the following boundary value problems:

Find a continuous solution $u(t,z)=\left(\begin{array}{c}{u}_1(t,z)\\ u_2(t,z)\end{array}\right)$ of the equation

$$Du=f$$

(25)

in $\overline{\mathrm{\Omega }}$, satisfying the boundary conditions

$$u_1{|}_S=\phi ,$$

(26)

$$Re\overline{\lambda (\tau )}{u}_2(0,\tau )=r(\tau ),\tau \in L,$$

(27)

where φ is a given complex value function on S, $\phi \in C(S)$, $\lambda (\tau )$ is a given complex value function on L, $\lambda (\tau )\ne 0$, $\tau \in L$. $r(\tau )$ is a given real value function on L, $\lambda (\tau )$, $r(\tau )\in C_{\alpha }$, $0<\alpha <1$. This problem is called problem H of the equation (25), and $\kappa =\frac{1}{2\pi }{\mathrm{△}}_{L}arg\lambda (\tau )$ is called index of the problem H.

When $\kappa =0$, if u satisfies the condition

$$Im{u}_2(0,0)=a$$

(28)

besides the above boundary conditions, where a is a real constant, then the problem is called problem D.

In particular, when $f=0$ in the equation (25), the above problems are namely the problem H and problem D for the $H_{\lambda }$-regular vector functions.

Lemma 2 Suppose complex value functions $g_1(t,z)$, $g_2(t,z)\in C(\overline{\mathrm{\Omega }})\cap C^1(\mathrm{\Omega })$. If $g_1(t,z)$, $g_2(t,z)$ satisfy compatible condition

$$(\lambda -\frac{\partial }{\partial t})g_1=\frac{\partial }{\partial \overline{z}}{g}_2,$$

(29)

then the following overdetermined system with respect to $u(t,z)$

$$\{\begin{array}{c}\frac{\partial }{\partial \overline{z}}u=g_1(t,z),\hfill \\ (\lambda -\frac{\partial }{\partial t})u=g_2(t,z)\hfill \end{array}$$

(30)

has the general solution

$$u(t,z)=T_{{\mathrm{\Omega }}_0}{g}_1+\mathrm{\Phi }(z)e^{\lambda t}-F(t,z)e^{\lambda t},$$

(31)

here $\mathrm{\Phi }(z)$ is any analytic function in ${\mathrm{\Omega }}_0$,

$$\begin{array}{c}{T}_{{\mathrm{\Omega }}_0}{g}_1=-\frac{1}{\pi }{\int }_{{\mathrm{\Omega }}_0}\frac{g_1(t,\zeta )}{\zeta -z}d{\sigma }_{\zeta },\hfill \\ F(t,z)={\int }_0^t{e}^{-\lambda \xi }\left(\frac{1}{2\pi i}{\int }_{\mathrm{\Gamma }}\frac{g_2(\xi ,\zeta )}{\zeta -z}d\zeta \right)d\xi .\hfill \end{array}$$

Proof Noting the compatible condition and that $F(t,z)$ is an analytic function with respect to z, using the Pompeiu formula [12], it is not difficult to verify by direct calculation that $u(t,z)$ expressed by (31) is the general solution of the system (30). □

As a special case of Theorem 6.13 in [4], we can derive the following result.

Lemma 3 If φ is continuous on S, then the Dirichlet problem with the boundary condition

$$w{|}_S=\phi$$

for the equation $({\lambda }^2-\mathrm{△})w=0$ in Ω has a unique solution $w(t,z)\in C(\overline{\mathrm{\Omega }})\cap C_{\alpha }^2(\mathrm{\Omega })$.

Similarly to harmonic function, we have the following result.

Lemma 4 For the Dirichlet problem of the equation $({\lambda }^2-\mathrm{△})w=0$ in Ω, Green functions $G(p,p^{\prime })$ exist such that the solutions of the problem can be represented by $G(p,p^{\prime })$, namely we have

$$w(p)=-{\int }_{S}w\left(p^{\prime }\right)\frac{\partial G}{\partial \nu }d{S}_{p^{\prime }}.$$

(32)

These Green functions $G(p,p^{\prime })$ are unique.

Proof Suppose functions $w,v\in C^1(\overline{\mathrm{\Omega }})\cap C^2(\mathrm{\Omega })$. By Green’s second identity

$${\int }_{\mathrm{\Omega }}(w\mathrm{△}v-v\mathrm{△}w)d\sigma ={\int }_S(w\frac{\partial v}{\partial \nu }-v\frac{\partial w}{\partial \nu })dS,$$

where ν denotes the unit outward normal to the surface S, we obtain

$${\int }_{\mathrm{\Omega }}\left\{v[({\lambda }^2-\mathrm{△})w-w({\lambda }^2-\mathrm{△})v]\right\}d\sigma ={\int }_S(w\frac{\partial v}{\partial \nu }-v\frac{\partial w}{\partial \nu })dS.$$

(33)

Let p be a fixed point in Ω and $B_{\epsilon }(p)=\{|p^{\prime }-p|<\epsilon \}$ be an open ball whose radius ε is so small that $\overline{B_{\epsilon }(p)}\subset \mathrm{\Omega }$. Write ${\mathrm{\Omega }}_{\epsilon }=\mathrm{\Omega }\setminus \overline{B_{\epsilon }(p)}$. Replacing v by $\frac{1}{4\pi }\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}$, using the formula (33) in ${\mathrm{\Omega }}_{\epsilon }$ and letting ε tend to zero, similarly to the proof of Theorem 1, we can derive

$$w(p)=-\frac{1}{4\pi }{\int }_S[w\frac{\partial }{\partial \nu }\left(\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}\right)-\left(\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}\right)\frac{\partial w}{\partial \nu }]dS+\frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}({\lambda }^2-\mathrm{△})wd\sigma .$$

Thus when $w\in C^1(\overline{\mathrm{\Omega }})\cap C^2(\mathrm{\Omega })$ and satisfies the equation $({\lambda }^2-\mathrm{△})w=0$,

$$w(p)=-\frac{1}{4\pi }{\int }_S[w\frac{\partial }{\partial \nu }\left(\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}\right)-\left(\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}\right)\frac{\partial w}{\partial \nu }]dS.$$

(34)

For a given p in Ω, find $g(p^{\prime },p)$ which satisfies the equation $({\lambda }^2-\mathrm{△})g=0$ in Ω and the boundary condition $g(p^{\prime },p)=\frac{1}{4\pi }\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}$ on S. By virtue of Lemma 3, this $g(p^{\prime },p)$ is existential and unique. Write $G(p,p^{\prime })=\frac{1}{4\pi }\frac{e^{-\lambda |p^{\prime }-p|}}{|p^{\prime }-p|}-g(p^{\prime },p)$. When w satisfies the equation $({\lambda }^2-\mathrm{△})w=0$ in Ω, from (33) we derive

$${\int }_S(w\frac{\partial g}{\partial \nu }-g\frac{\partial w}{\partial \nu })dS=0.$$

Subtracting this from (34), we get

$$w(p)=-{\int }_{S}w\left(p^{\prime }\right)\frac{\partial G}{\partial \nu }d{S}_{p^{\prime }}.$$

A simple approximation argument shows that this formula continues to hold for $w\in C(\overline{\mathrm{\Omega }})\cap C^2(\mathrm{\Omega })$. □

With the aid of the methods of conformal mapping and standardizing boundary condition from complex analysis (see [12, 13]), we can map conformally ${\mathrm{\Omega }}_0$ into the unit disk on the plane $t=0$, and transform $\lambda (\tau )$ in the condition (33) into ${\tau }^{\kappa }$. Hence without loss of generality, we shall directly suppose that ${\mathrm{\Omega }}_0$ is the unit disk $B_1(0)$ on the plane $t=0$ and replace (27) by the following condition

$$Re{\overline{\tau }}^{\kappa }{u}_2(0,\tau )=r(\tau ),\tau \in L=\partial B_1(0).$$

(35)

Using these results, we can discuss the solvability of the problem H and the problem D for the $H_{\lambda }$-regular vector functions and the equation $Du=f$.

Theorem 9 (1) If the index $\kappa \ge 0$, the problem H for the $H_{\lambda }$-regular vector functions in Ω is solvable. The problem has the general solutions $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$, with

$${\psi }_1(t,z)=-{\int }_S\phi \left(p^{\prime }\right)\frac{\partial G}{\partial \nu }d{S}_{p^{\prime }},$$

(36)

$${\psi }_2(t,z)=T_{B_1(0)}{g}_1+\mathrm{\Phi }(z)e^{\lambda t}-F(t,z)e^{\lambda t},$$

(37)

where

$$\begin{array}{c}{g}_1=\frac{1}{2}(\lambda +\frac{\partial }{\partial t}){\psi }_1,\hfill \\ g_2(t,z)=-2\frac{\partial }{\partial z}{\psi }_1,\hfill \\ \mathrm{\Phi }(z)=-\frac{1}{\pi }{\int }_{B_1(0)}\frac{z^{2\kappa +1}\overline{g_1(0,\zeta )}}{1-\overline{\zeta }z}d{\sigma }_{\zeta }+\frac{z^{\kappa }}{2\pi i}{\int }_{L}r(\tau )\frac{\tau +z}{\tau -z}\frac{d\tau }{\tau }+\sum _{m=0}^{2\kappa }{c}_m{z}^m,\hfill \end{array}$$

here $c_m$, $m=0,\dots ,\kappa$ are arbitrary complex constants, satisfying

$$c_{2\kappa -m}+\overline{c_m}=0.$$

• (2) If the index $\kappa <0$, the problem H for the $H_{\lambda }$-regular vector functions in Ω is solvable if and only if the function $r(\tau )$ in the boundary conditions (27) satisfies the following conditions

  

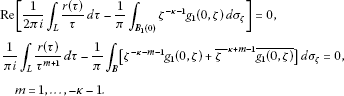  (38)

When the conditions (38) hold, the solution then has the same expression as (1), except that

$$\mathrm{\Phi }(z)=-\frac{1}{\pi }{\int }_{B_1(0)}\frac{{\overline{\zeta }}^{-2\kappa -1}\overline{g_1(0,\zeta )}}{1-\overline{\zeta }z}d{\sigma }_{\zeta }+\frac{1}{\pi i}{\int }_L\frac{r(\tau )}{{\tau }^{-\kappa }(\zeta -z)}d\tau .$$

Proof If $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ is a $H_{\lambda }$-regular vector function, then $\mathrm{\Psi }(t,z)$ satisfies the equation $D\mathrm{\Psi }=0$ which is equivalent to

$$\{\begin{array}{c}\frac{\partial }{\partial \overline{z}}{\psi }_2=-\frac{1}{2}(\lambda +\frac{\partial }{\partial t}){\psi }_1=g_1(t,z),\hfill \\ (\lambda -\frac{\partial }{\partial t}){\psi }_2=-2\frac{\partial }{\partial z}{\psi }_1=g_2(t,z).\hfill \end{array}$$

(39)

From Lemma 4, the function ${\psi }_1(t,z)$ expressed in (36) is the unique solution of the Dirichlet problem with the boundary condition (26) for the equation $({\lambda }^2-\mathrm{△})w=0$ in Ω, so that $g_1(t,z)$, $g_2(t,z)$ satisfy the compatible condition of Lemma 2

$$(\lambda -\frac{\partial }{\partial t})g_1=\frac{\partial }{\partial \overline{z}}{g}_2.$$

(40)

Consequently, ${\psi }_2(t,z)$ can be given by the formula (37). Furthermore, ${\psi }_2(t,z)$ expressed in (37) satisfies the boundary condition (35) if and only if the analytic function $\mathrm{\Phi }(z)$ satisfies the following boundary condition

$$Re{\overline{\tau }}^{\kappa }\mathrm{\Phi }(\tau )=r(\tau )-Re{\overline{\tau }}^{\kappa }{T}_{B_1(0)}{g}_1(0,\tau ),\tau \in L.$$

(41)

By means of the results about the Riemann-Hilbert boundary value problem for analytic function in the unit disk [13], we can derive the solvable conditions and the expression of solutions. □

Corollary 2 The problem D for the $H_{\lambda }$-regular vector functions in Ω has a unique solution, and the solution is $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ which ${\psi }_1(t,z)$ is given by (36) and ${\psi }_2(t,z)$ expressed as (37) where

$$\mathrm{\Phi }(z)=-\frac{1}{\pi }{\int }_{B_1(0)}\frac{z\overline{g_1(0,\zeta )}}{1-\overline{\zeta }z}d{\sigma }_{\zeta }+\frac{1}{2\pi i}{\int }_{L}r(\tau )\frac{\tau +z}{\tau -z}\frac{d\tau }{\tau }+i(a-Im{T}_{B_1(0)}{g}_1(0,z)).$$

Proof The result follows immediately from Theorem 9 and the results of the Dirichlet boundary value problem for analytic function in the unit disk. □

Since the solution u of the equation $Du=f$ can be expressed as $u=\mathrm{\Psi }+T_{\mathrm{\Omega }}f$, where Ψ is any $H_{\lambda }$-regular vector functions in Ω, if $f\in L_p(\overline{\mathrm{\Omega }})$, $p>3$, then $T_{\mathrm{\Omega }}f\in C_{\alpha }(\overline{\mathrm{\Omega }})$, therefore the problem H of the equation $Du=f$ in Ω can be transformed into the problem H of the $H_{\lambda }$-regular vector function $\mathrm{\Psi }(t,z)=\left(\begin{array}{c}{\psi }_1(t,z)\\ {\psi }_2(t,z)\end{array}\right)$ in Ω with the following boundary conditions

$$\begin{array}{c}{\psi }_1(t,z)={\phi }_1(t,z)=\phi (t,z)-T_{\mathrm{\Omega }}^{1}f,(t,z)\in S,\hfill \\ Re{\overline{\tau }}^{\kappa }{\psi }_2(0,\tau )=r_1(\tau )=r(\tau )-Re{\overline{\tau }}^{\kappa }{T}_{\mathrm{\Omega }}^{2}f,\tau \in L,\hfill \end{array}$$

where

$$\begin{array}{rcl}{T}_{\mathrm{\Omega }}^{1}f& =& \frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\{\frac{\lambda e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{|{\zeta }^{\prime }-\zeta |}{f}_1\\ -(\frac{\lambda }{{|{\zeta }^{\prime }-\zeta |}^2}+\frac{1}{{|{\zeta }^{\prime }-\zeta |}^3})e^{-\lambda |{\zeta }^{\prime }-\zeta |}[(t^{\prime }-t)f_1+(z^{\prime }-z)f_2]\}d{\sigma }_{{\zeta }^{\prime }},\\ T_{\mathrm{\Omega }}^{2}f& =& \frac{1}{4\pi }{\int }_{\mathrm{\Omega }}\{\frac{\lambda e^{-\lambda |{\zeta }^{\prime }-\zeta |}}{|{\zeta }^{\prime }-\zeta |}{f}_2\\ -(\frac{\lambda }{{|{\zeta }^{\prime }-\zeta |}^2}+\frac{1}{{|{\zeta }^{\prime }-\zeta |}^3})e^{-\lambda |{\zeta }^{\prime }-\zeta |}[({\overline{z}}^{\prime }-\overline{z})f_1-(t^{\prime }-t)f_2]\}d{\sigma }_{{\zeta }^{\prime }},\end{array}$$

namely $T_{\mathrm{\Omega }}f=\left(\begin{array}{c}{T}_{\mathrm{\Omega }}^{1}f\\ T_{\mathrm{\Omega }}^{2}f\end{array}\right)$. Using Theorem 10, we obtain the following result about the problem H for the equation $Du=f$ in Ω.

Theorem 10 Let $f\in L_p(\overline{\mathrm{\Omega }})$, $p>3$.

(a) If the index $\kappa \ge 0$, the problem H for the equation $Du=f$ in Ω has the solution $u(t,z)=\mathrm{\Psi }(t,z)+T_{\mathrm{\Omega }}f$, where the $H_{\lambda }$-regular vector function $\mathrm{\Psi }(t,z)$ is expressed as (a) of Theorem  9 with ${\phi }_1(t,z)$, $r_1(\tau )$ replacing $\phi (t,z)$, $r(\tau )$ respectively.

(b) If the index $\kappa <0$, replacing $\phi (t,z)$ by ${\phi }_1(t,z)$, the problem H for the equation $Du=f$ in Ω is solvable if and only if the function $r_1(\tau )$ satisfies the conditions (38). When the conditions (38) hold, the problem then has the solution $u(t,z)=\mathrm{\Psi }(t,z)+T_{\mathrm{\Omega }}f$, where the $H_{\lambda }$-regular vector function $\mathrm{\Psi }(t,z)$ is expressed as (b) of Theorem  9 with ${\phi }_1(t,z)$, $r_1(\tau )$ replacing $\phi (t,z)$, $r(\tau )$ respectively.

In the same way, we can obtain the result about the problem D for the equation $Du=f$ in Ω.

Corollary 3 Suppose that $f\in L_p(\overline{\mathrm{\Omega }}),p>3$. The problem D for the equation $Du=f$ in Ω has a unique solution $u(t,z)=\mathrm{\Psi }(t,z)+T_{\mathrm{\Omega }}f$, where the $H_{\lambda }$-regular vector function $\mathrm{\Psi }(t,z)$ is expressed as Corollary  2 with ${\phi }_1(t,z)$, $r_1(\tau )$ and $a_1=a-Im{T}_{\mathrm{\Omega }}^{2}f$ replacing $\phi (t,z)$, $r(\tau )$ and a respectively.