Existence of solutions to strongly damped plate or beam equations

Abstract

In this paper, we study a strongly damped plate or beam equation. By using spatial sequence techniques and energy estimate methods, we obtain an existence theorem of the solution to abstract strongly damped plate or beam equation and to a nonlinear plate or beam equation.

MSC:35L05, 35L20, 35D30, 35D35.

1 Introduction

We consider the following nonlinear strongly damped plate or beam equation:

$$\{\begin{array}{c}\frac{{\partial }^{2}u}{\partial t^2}-k\frac{\partial \mathrm{△}u}{\partial t}=f(x,{\mathrm{△}}^{2}u)+g(x,u,Du,D^{2}u,D^{3}u),k>0,\hfill \\ u{|}_{\partial \mathrm{\Omega }}=\mathrm{△}u{|}_{\partial \mathrm{\Omega }}=0,\hfill \\ u(x,0)=\phi ,u_t(x,0)=\psi ,\hfill \end{array}$$

(1.1)

where Δ is the Laplacian operator, Ω denotes an open bounded set of $R^N$ ($N=1,2$) with a smooth boundary ∂ Ω and u denotes a vertical displacement at $(x,t)$.

It is well known that flexible structures like suspension bridges or overhead power transmission lines can be subjected to oscillations due to various causes. Simple models for such oscillations are described with second- and fourth-order partial differential equations as can be seen for example in [1–8]. The problem (1.1) can be applied in the mechanics of elastic constructions for the study of equilibrium forms of the plate and beam, which has a long history. The abstract theory of Eq. (1.1) was investigated by several authors [9–14].

The main objective of this article is to find proper conditions on f and g to ensure the existence of solutions of Eq. (1.1). This article uses the spatial sequence techniques, each side of the equation to be treated in different spaces, which is an important way to get more extensive and wonderful results.

The outline of the paper is as follows. In Section 2 we provide an essential definition and lemma of solutions to abstract equations from [15–18]. In Section 3, we give an existence theorem of solutions to abstract strongly damped plate or beam equations. In Section 4.10, we present the main result and its proof.

2 Preliminaries

We introduce two spatial sequences:

$$\{\begin{array}{c}X\subset H_3\subset X_2\subset X_1\subset H,\hfill \\ X_2\subset H_2\subset H_1\subset H,\hfill \end{array}$$

(2.1)

where H, $H_1$, $H_2$, $H_3$ are Hilbert spaces, X is a linear space, and $X_1$, $X_2$ are Banach spaces. All embeddings of (2.1) are dense. Let

$$\{\begin{array}{c}L:X\to X_1\text{be one-one dense linear operator},\hfill \\ {〈Lu,v〉}_H={〈u,v〉}_{H_1},\mathrm{\forall }u,v\in X.\hfill \end{array}$$

(2.2)

Furthermore, L has eigenvectors $\{e_k\}$ satisfying

$$L{e}_k={\lambda }_k{e}_k(k=1,2,\dots ),$$

(2.3)

and $\{e_k\}$ constitutes a common orthogonal basis of H and $H_3$.

We consider the following abstract equation:

$$\{\begin{array}{c}\frac{d^{2}u}{d{t}^2}+k\frac{d}{dt}\mathcal{L}u=G(u),k>0,\hfill \\ u(0)=\phi ,u_t(0)=\psi ,\hfill \end{array}$$

(2.4)

where $G:X_2\times R^{+}\to X_1^{\ast }$ is a mapping, $R^{+}=[0,\mathrm{\infty })$ and $\mathcal{L}:X_2\to X_1$ is a bounded linear operator satisfying

$${〈\mathcal{L}u,Lv〉}_H={〈u,v〉}_{H_2},\mathrm{\forall }u,v\in X_2.$$

(2.5)

Definition 2.1[15]

We say $u\in W_{\mathrm{loc}}^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap L_{\mathrm{loc}}^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2)$ is a global weak solution of Eq. (2.4) provided that $(\phi ,\psi )\in X_2\times H_1$

$${〈u_t,v〉}_H+k{〈\mathcal{L}u,v〉}_H={\int }_0^t〈G(u),v〉dt+{〈\psi ,v〉}_H+k{〈\mathcal{L}\phi ,v〉}_H,$$

(2.6)

for all $v\in X_1$ and $0\le t<\mathrm{\infty }$.

Lemma 2.2[18]

Let$u\in L_{\mathrm{loc}}^p((-\mathrm{\infty },\mathrm{\infty }),X)$, X be a Banach space. If$u_h=\frac{1}{h}{\int }_h^{t+h}u(s)ds$ ($0<|h|<1$), then$\{u_h\}\in L_{\mathrm{loc}}^p((-\mathrm{\infty },\mathrm{\infty }),X)$, satisfying

3 Existence theorem of abstract equation

Let $G=A+B:X_2\times R^{+}\to X_1^{\ast }$. Assume:

(A1) There is a $C^1$ functional $F:X_2\to R^1$ such that

$$〈Au,Lv〉=〈-DF(u),v〉,\mathrm{\forall }u,v\in X.$$

(3.1)

(A2) Functional $F:X_2\to R^1$ is coercive, i.e.,

$$F(u)\to \mathrm{\infty },\iff {\parallel u\parallel }_{X_2}\to \mathrm{\infty }.$$

(3.2)

(A3) B satisfies

$$|〈Bu,Lv〉|\le CF(u)+\frac{k}{2}{\parallel v\parallel }_{H_2}^2+g(t),\mathrm{\forall }u,v\in X,$$

(3.3)

for $g\in L_{\mathrm{loc}}^1(0,\mathrm{\infty })$.

Theorem 3.1 If$G:X_2\times R^{+}\to X_1^{\ast }$is bounded and continuous, and DF is monotone, i.e.,

$$〈DF(u_1)-DF(u_2),u_1-u_2〉\ge 0,\mathrm{\forall }{u}_1,u_2\in X_2,$$

(3.4)

then, for all$(\phi ,\psi )\in X_2\times H_1$, the following assertions hold.

• (1) If $G=A$ satisfies (A 1) and (A 2), then Eq. (2.4) has a global weak solution

  $$u\in W^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W^{1,2}((0,\mathrm{\infty }),H_2)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2).$$

  (3.5)

• (2) If $G=A+B$ satisfies (A 1)-(A 3), and $u_n{\rightharpoonup }^{\ast }{u}_0$ in $L^{\mathrm{\infty }}((0,T),X_2)$ such that

  

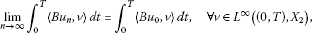  (3.6)

(3.7)

then Eq. (2.4) has a global weak solution

$$u\in W_{\mathrm{loc}}^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W_{\mathrm{loc}}^{1,2}((0,\mathrm{\infty }),H_2)\cap L_{\mathrm{loc}}^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2).$$

(3.8)

• (3) Furthermore, if $G=A+B$ satisfies

  $$|〈Gu,v〉|\le CF(u)+\frac{1}{2}{\parallel v\parallel }_H^2+g(t),$$

  (3.9)

for$g\in L^1(0,T)$, then$u\in W_{\mathrm{loc}}^{2,2}((0,\mathrm{\infty });H)$.

Proof Let $\{e_k\}\subset X$ be a common orthogonal basis of H and $H_3$, satisfying (2.3). Set

$$\{\begin{array}{c}{X}_n=\{\sum _{i=1}^n{\alpha }_i{e}_i|{\alpha }_i\in R^1\},\hfill \\ {\tilde{X}}_n=\{\sum _{j=1}^n{\beta }_j(t)e_j|{\beta }_j\in C^2[0,\mathrm{\infty })\}.\hfill \end{array}$$

(3.10)

Clearly, $L{X}_n=X_n$, $L{\tilde{X}}_n={\tilde{X}}_n$.

By using Galerkin method, there exists $u_n\in C^2([0,\mathrm{\infty }),X_n)$ satisfying

$$\{\begin{array}{c}{〈\frac{d{u}_n}{dt},v〉}_H+k{〈\mathcal{L}{u}_n,v〉}_H={\int }_0^t〈G(u_n),v〉dt+{〈{\psi }_n,v〉}_H+k{〈\mathcal{L}{\phi }_n,v〉}_H,\hfill \\ u_n(0)={\phi }_n,u_n^{\prime }(0)={\psi }_n,\hfill \end{array}$$

(3.11)

for $\mathrm{\forall }v\in X_n$, and

$${\int }_0^t[{〈\frac{d^2{u}_n}{d^{2}t},v〉}_H+k{〈\mathcal{L}\frac{d{u}_n}{dt},v〉}_H]dt={\int }_0^t〈G{u}_n,v〉dt$$

(3.12)

for $\mathrm{\forall }v\in {\tilde{X}}_n$.

Firstly, we consider $G=A$. Let $v=\frac{d}{dt}L{u}_n$ in (3.12). Taking into account (2.2)and (3.1), it follows that

$$\begin{array}{rcl}0& =& {\int }_0^t[\frac{1}{2}\frac{d}{dt}{〈\frac{d{u}_n}{dt},\frac{d{u}_n}{dt}〉}_{H_1}+k{〈\frac{d{u}_n}{dt},\frac{d{u}_n}{dt}〉}_{H_2}+〈DF(u_n),\frac{d{u}_n}{dt}〉]dt\\ =& \frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2-\frac{1}{2}{\parallel {\psi }_n\parallel }_{H_1}^2+k{\int }_0^t{\parallel \frac{d{u}_n}{dt}\parallel }_{H_2}^{2}dt+F(u_n)-F({\phi }_n).\end{array}$$

We get

$$\frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2+k{\int }_0^t{\parallel \frac{d{u}_n}{dt}\parallel }_{H_2}^{2}dt+F(u_n)=F({\phi }_n)+\frac{1}{2}{\parallel {\psi }_n\parallel }_{H_1}^2.$$

(3.13)

Let $\phi \in H_3$. From (2.1) and (2.2), it is known that $\{e_n\}$ is an orthogonal basis of $H_1$. We find that ${\phi }_n\to \phi$ in $H_3$, and ${\psi }_n\to \psi$ in $H_1$. From that $H_3\subset X_2$ is an imbedding, it follows that

$$\{\begin{array}{c}{\phi }_n\to \phi \text{in }{X}_2,\hfill \\ {\psi }_n\to \psi \text{in }{H}_1.\hfill \end{array}$$

(3.14)

From (3.2), (3.13) and (3.14), we obtain

$$\{u_n\}\subset W^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W^{1,2}((0,\mathrm{\infty }),H_2)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2)\text{ is bounded}.$$

Let

$$\{\begin{array}{c}{u}_n{\rightharpoonup }^{\ast }{u}_0\text{in }{W}^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2),\hfill \\ u_n\rightharpoonup u_0\text{in }{W}^{1,2}((0,\mathrm{\infty }),H_2),\hfill \end{array}$$

(3.15)

which implies that $u_n\to u_0$ in $W^{1,2}((0,\mathrm{\infty }),H)$ is uniformly weakly convergent from that $H_2\subset H$ is a compact imbedding.

According to (2.2), (2.4), (2.5) and (3.4), we obtain that

$$\begin{array}{rcl}0& \ge & {\int }_0^t〈DF(v)-DF(u_n),u_n-v〉d\tau \\ =& {\int }_0^t〈Av,Lv-L{u}_n〉d\tau +{\int }_0^t〈A{u}_n,L{u}_n-Lv〉d\tau \\ =& {\int }_0^t〈Av,Lv-L{u}_n〉d\tau +{\int }_0^t{〈\frac{d^2{u}_n}{d{t}^2}+k\frac{d}{dt}\mathcal{L}{u}_n,L{u}_n-Lv〉}_{H}d\tau \\ =& {\int }_0^t〈Av,Lv-L{u}_n〉d\tau +{\int }_0^t{〈\frac{d^2{u}_n}{d{t}^2},L{u}_n〉}_{H}d\tau +k{\int }_0^t{〈\frac{d}{dt}\mathcal{L}{u}_n,L{u}_n〉}_{H}d\tau \\ -{\int }_0^t{〈\frac{d^2{u}_n}{d{t}^2},Lv〉}_{H}d\tau -k{\int }_0^t{〈\frac{d}{dt}\mathcal{L}{u}_n,Lv〉}_{H}d\tau \\ =& {\int }_0^t〈Av,Lv-L{u}_n〉d\tau +{\int }_0^t{〈\frac{d^2{u}_n}{d{t}^2},u_n〉}_{H_1}d\tau +k{\int }_0^t{〈\frac{d{u}_n}{dt},u_n〉}_{H_2}d\tau \\ -{\int }_0^t{〈\frac{d^2{u}_n}{d{t}^2},v〉}_{H_1}d\tau -k{\int }_0^t{〈\frac{d{u}_n}{dt},v〉}_{H_2}d\tau \\ =& {\int }_0^t〈Av,Lv-L{u}_n〉d\tau +{〈u_n,\frac{d{u}_n}{dt}〉}_{H_1}-{〈{\phi }_n,{\psi }_n〉}_{H_1}-{\int }_0^t{〈\frac{d{u}_n}{dt},\frac{d{u}_n}{dt}〉}_{H_1}d\tau \\ +\frac{k}{2}{〈u_n,u_n〉}_{H_2}-\frac{k}{2}{〈{\phi }_n,{\phi }_n〉}_{H_2}-{〈\frac{d{u}_n}{dt},v〉}_{H_1}+{〈{\psi }_n,v(0)〉}_{H_1}+{\int }_0^t{〈\frac{d{u}_n}{dt},\frac{dv}{dt}〉}_{H_1}d\tau \\ -k{〈u_n,v〉}_{H_2}+k{〈{\phi }_n,v(0)〉}_{H_2}+k{\int }_0^t{〈u_n,\frac{dv}{dt}〉}_{H_2}d\tau .\end{array}$$

Let $n\to \mathrm{\infty }$. From (3.15), we get

(3.16)

Since ${\bigcup }_{n=1}^{\mathrm{\infty }}{\tilde{X}}_n$ is dense in $W^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W^{1,2}((0,\mathrm{\infty }),H_2)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2)$, the above equality (3.16) holds for $\mathrm{\forall }v\in W^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W^{1,2}((0,\mathrm{\infty }),H_2)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2)$.

We set v the following variable:

where $w\in X_2$, λ is a real, ${\tilde{u}}_0=u_0$ if $t\ge 0$, and ${\tilde{u}}_0=0$ if $t<0$. Thus the equality (3.16) is read as

(3.17)

and,

(3.18)

In view of (3.17) and (3.18), we have

(3.19)

We know that

and

Let $h\to 0^{+}$. (3.19) can be read as

$${\int }_0^t〈A(u_0+\lambda w),\lambda Lw〉d\tau -{〈\frac{d{u}_0}{dt},\lambda w〉}_{H_1}-k{〈u_0,\lambda w〉}_{H_2}+{〈\psi ,\lambda w〉}_{H_1}+k{〈\phi ,\lambda w〉}_{H_2}\le 0.$$

According to (2.2) and (2.5), we obtain that

$${\int }_0^t〈A(u_0+\lambda w),Lw〉d\tau -{〈\frac{d{u}_0}{dt},Lw〉}_H-k{〈\mathcal{L}{u}_0,Lw〉}_H+{〈\psi ,Lw〉}_{H_1}+k{〈\mathcal{L}\phi ,Lw〉}_H\le 0.$$

Let $\lambda \to 0^{+}$. It follows that

$${\int }_0^t〈A(u_0),Lw〉d\tau -{〈\frac{d{u}_0}{dt},Lw〉}_H-k{〈\mathcal{L}{u}_0,Lw〉}_H+{〈\psi ,Lw〉}_{H_1}+k{〈\mathcal{L}\phi ,Lw〉}_H\le 0.$$

Since $L:X_2\to X_1$ is dense, the above inequality can be rewritten as

$${〈\frac{d{u}_0}{dt},v〉}_H+k{〈\mathcal{L}{u}_0,v〉}_H={\int }_0^t〈A(u_0),v〉d\tau +{〈\psi ,v〉}_H+k{〈\mathcal{L}\phi ,v〉}_H,$$

which implies that $u_0\in W^{1,\mathrm{\infty }}((0,\mathrm{\infty }),H_1)\cap W^{1,2}((0,\mathrm{\infty }),H_2)\cap L^{\mathrm{\infty }}((0,\mathrm{\infty }),X_2)$ is a global weak solution of Eq. (2.4).

Secondly, we consider $G=A+B$. Let $v=\frac{d}{dt}L{u}_n$ in (3.12). In view of (2.2) and (3.1), it follows that

$$\frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2+k{\int }_0^t{\parallel \frac{d{u}_n}{dt}\parallel }_{H_2}^{2}dt+F(u_n)={\int }_0^t〈B(u_n),\frac{d}{dt}L{u}_n〉dt+F({\phi }_n)+\frac{1}{2}{\parallel {\psi }_n\parallel }_{H_1}^2.$$

From (3.3), we have

$$\frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2+F(u_n)+k{\int }_0^t{\parallel \frac{d{u}_n}{dt}\parallel }_{H_2}^{2}dt\le C{\int }_0^t[F(u_n)+\frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2]dt+f(t),$$

(3.20)

where $f(t)={\int }_0^{t}g(\tau )d\tau +\frac{1}{2}{\parallel \psi \parallel }_{H_1}^2+{sup}_{n}F({\phi }_n)$.

By using the Gronwall inequality, it follows that

$$\frac{1}{2}{\parallel \frac{d{u}_n}{dt}\parallel }_{H_1}^2+F(u_n)\le f(0)e^{Ct}+{\int }_0^{t}f(\tau )e^{C(t-\tau )}d\tau ,$$

(3.21)

which implies that for all $0<T<\mathrm{\infty }$,

$$\{u_n\}\subset W^{1,\mathrm{\infty }}((0,T),H_1)\cap L^{\mathrm{\infty }}((0,T),X_2)\text{ is bounded}.$$

From (3.20) and (3.21), it follows that

$$\{u_n\}\subset W^{1,2}((0,T),H_2)\text{ is bounded}.$$

Let

$$\{\begin{array}{c}{u}_n{\rightharpoonup }^{\ast }{u}_0\text{in }{W}^{1,\mathrm{\infty }}((0,T),H_1)\cap L^{\mathrm{\infty }}((0,T),X_2),\hfill \\ u_n\rightharpoonup u_0\text{in }{W}^{1,2}((0,T),H_2),\hfill \end{array}$$

(3.22)

which implies that $u_n\to u_0$ in $W^{1,2}((0,T),H)$ is uniformly weakly convergent from that $H_2\subset H$ is a compact imbedding.

The remaining part of the proof is same as assertion (1).

Lastly, assume (3.9) holds. Let $v=\frac{d^2{u}_n}{d{t}^2}$ in (3.12). It follows that

From (3.21), the above inequality implies

$${\int }_0^t{\parallel \frac{d^2{u}_n}{d{t}^2}\parallel }_H^{2}d\tau \le C(C>0\text{ is constant}).$$

(3.23)

We see that for all $0<T<\mathrm{\infty }$, $\{u_n\}\subset W^{2,2}((0,T),H)$ is bounded. Thus $u\in W^{2,2}((0,T),H)$. □

4 Main result

Now, we consider the nonlinear strongly damped plate or beam equation (1.1). Set

$$F(x,y)={\int }_0^{y}f(x,z)dz.$$

(4.1)

We assume

(4.2)

(4.3)

(4.4)

(4.5)

(4.6)

where $\xi =\{{\xi }_{\alpha }||\alpha |\le 3\}$, ${\xi }_{\alpha }$ corresponds to $D^{\alpha }u$.

Theorem 4.1 Under the assumptions (4.1)-(4.6), if φ satisfies the bounded condition of Eq. (1.1), for$(\phi ,\psi )\in W^{4,p}(\mathrm{\Omega })\cap H^2\times H_0^1(\mathrm{\Omega })$, then there exists a global strong solution for Eq. (1.1)

Proof We introduce spatial sequences

$$\begin{array}{c}X=\{u\in C^{\mathrm{\infty }}(\mathrm{\Omega }){\left|{\mathrm{△}}^{k}u\right|}_{\partial \mathrm{\Omega }}=0,k=0,1,2,\dots \},\hfill \\ X_1=L^p(\mathrm{\Omega }),X_2=\{W^{4,p}(\mathrm{\Omega }){|u|}_{\partial \mathrm{\Omega }}=\mathrm{△}u{|}_{\partial \mathrm{\Omega }}=0\},\hfill \\ H=L^2(\mathrm{\Omega }),H_1=H^2(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega }),\hfill \\ H_2=\{H^3(\mathrm{\Omega }){|u|}_{\partial \mathrm{\Omega }}=\mathrm{△}u{|}_{\partial \mathrm{\Omega }}=0\},\hfill \\ H_3=\{u\in H^{4m}(\mathrm{\Omega }){|u|}_{\partial \mathrm{\Omega }}=\cdots ={\mathrm{△}}^{2m-1}u{|}_{\partial \mathrm{\Omega }}\},\hfill \end{array}$$

where the inner products of $H_1$, $H_2$ and $H_3$ are defined by

$$\begin{array}{c}{〈u,v〉}_{H_1}={\int }_{\mathrm{\Omega }}\mathrm{△}u\mathrm{△}vdx,{〈u,v〉}_{H_2}={\int }_{\mathrm{\Omega }}▽\mathrm{△}u▽\mathrm{△}vdx,\hfill \\ {〈u,v〉}_{H_3}={\int }_{\mathrm{\Omega }}{\mathrm{△}}^{2m}u{\mathrm{△}}^{2m}vdx,\hfill \end{array}$$

where $m\ge 1$ such that $H_3\subset X_2$ is an embedding.

Linear operator $\mathcal{L}:X_2\to X_1$ and $L:X_2\to X_1$ is defined by

$$\mathcal{L}u=-\mathrm{△}u,Lu={\mathrm{△}}^{2}u.$$

It is known that $\mathcal{L}$ and L satisfy (2.2), (2.3) and (2.5). Define $G=A+B:X_2\to X_1^{\ast }$ by

$$〈Au,v〉={\int }_{\mathrm{\Omega }}f(x,{\mathrm{△}}^{2}u)vdx,〈Bu,v〉={\int }_{\mathrm{\Omega }}g(x,u,Du,D^{2}u,D^{3}u)vdx,\text{for }v\in X_1.$$

Let $F_1(u)={\int }_{\mathrm{\Omega }}F(x,\mathrm{△}u)dx$, where F is the same as in (4.2). We get

which implies conditions (A1), (A2) of Theorem 3.1.

From (4.3), we have

$$〈D{F}_1(u_1)-D{F}_1(u_2),u_1-u_2〉\ge 0.$$

From (4.5) and (4.6), we obtain that $B:X_2\to X_1^{\ast }$ is a compact operator. Then, B satisfies (3.6) and (3.7).

We will show (3.3) as follows. From (4.4) and (4.5), for $\mathrm{\forall }u,v\in X$, it follows that

$$\begin{array}{rcl}|〈Bu,Lv〉|& =& {\int }_{\mathrm{\Omega }}\left|g(x,u,Du,D^{2}u,D^{3}u){\mathrm{△}}^{2}v\right|dx\\ =& {\int }_{\mathrm{\Omega }}|\mathrm{\nabla }g(x,u,Du,D^{2}u,D^{3}u)\cdot ▽\mathrm{△}v|dx\\ \le & \frac{k}{2}{\int }_{\mathrm{\Omega }}{|▽\mathrm{△}v|}^{2}dx+\frac{2}{k}{\int }_{\mathrm{\Omega }}{|▽g(x,u,Du,D^{2}u,D^{3}u)|}^{2}dx\\ \le & \frac{k}{2}{\parallel v\parallel }_{H_2}^2+C{\int }_{\mathrm{\Omega }}[{|D_{x}g|}^2+\sum _{i=1}^n\sum _{|\alpha |\le 3}{|D_{{\zeta }_{\alpha }}g|}^2{\left|D_i{D}^{\alpha }u\right|}^2]dx\\ \le & \frac{k}{2}{\parallel v\parallel }_{H_2}^2+C{\int }_{\mathrm{\Omega }}[\sum _{|\alpha |\le 4}{\left|D^{\alpha }u\right|}^p+1]dx,\end{array}$$

which implies condition (A3) of Theorem 3.1. From Theorem 3.1, Eq. (1.1) has a solution

(4.7)

(4.8)

Lastly, we show that $u^{″}\in L^{p^{\prime }}(\mathrm{\Omega }\times (0,T))$. By Definition 2.1, u satisfies

$$\begin{array}{rcl}{\int }_{\mathrm{\Omega }}{u}_t(x,t)vdx+{\int }_{\mathrm{\Omega }}u(x,t)vdx& =& {\int }_0^t{\int }_{\mathrm{\Omega }}[f(x,\mathrm{△}u)+g(x,u,Du,D^{2}u,D^{3}u)v]dxdt\\ +{\int }_{\mathrm{\Omega }}\psi vdx+{\int }_{\mathrm{\Omega }}\phi vdx,\mathrm{\forall }v\in L^p(\mathrm{\Omega }).\end{array}$$

Then, for any $h>0$, it follows that

(4.9)

where ${\mathrm{△}}_h^{t}u=\frac{1}{h}(u(t+h)-u(t))$. Let $v={|{\mathrm{△}}_h^t{u}_t|}^{p^{\prime }-2}{\mathrm{△}}_h^t{u}_t$. From (4.9), we have

Then, it follows that

From (4.2) and (4.5), we have

$$\begin{array}{c}{\int }_0^T{\int }_{\mathrm{\Omega }}{\left|\frac{u_t(x,t+h)-u_t(x,t)}{h}\right|}^{p^{\prime }}dxdt\hfill \\ \le C{\int }_0^T{\int }_{\mathrm{\Omega }}{|{\mathrm{△}}_h^{t}u(x,t)|}^{p^{\prime }}dxdt\hfill \\ +C{\int }_0^T{\int }_t^{t+h}{\int }_{\mathrm{\Omega }}[{|f|}^{p^{\prime }}+{|g|}^{p^{\prime }}]dxd\tau dt\hfill \\ \le C{\int }_0^T{\int }_{\mathrm{\Omega }}{|u_t(x,t)|}^{\frac{p}{p-1}}dxdt\hfill \\ +C{\int }_0^T{\int }_{\mathrm{\Omega }}[{({|\mathrm{△}u|}^{p-1}+1)}^{p^{\prime }}+{(\sum _{|\alpha |\le 3}{\left|D^{\alpha }u\right|}^{\frac{p}{2}}+1)}^{p^{\prime }}]dxdt\hfill \\ \le C{\int }_0^T{\int }_{\mathrm{\Omega }}{|u_t(x,t)|}^{\frac{p}{p-1}}dxdt+C{\int }_0^T{\int }_{\mathrm{\Omega }}[{|\mathrm{△}u|}^p+\sum _{|\alpha |\le 3}{\left|D^{\alpha }u\right|}^{\frac{p^2}{2(p-1)}}+1]dxdt.\hfill \end{array}$$

By using the Sobolev embedding theorem, it follows that from (4.7) and (4.8) the right of the above inequality is bounded. Then, $u_{tt}$ exists almost everywhere in $\mathrm{\Omega }\times (0,T)$, and $u_{tt}\in L^{p^{\prime }}(\mathrm{\Omega }\times (0,T))$, $\mathrm{\forall }0<T<\mathrm{\infty }$. □