- Research
- Open access
- Published:
Nonlocal nonlinear integrodifferential equations of fractional orders
Boundary Value Problems volume 2012, Article number: 78 (2012)
Abstract
In this paper, Schauder fixed point theorem, Gelfand-Shilov principles combined with semigroup theory are used to prove the existence of mild and strong solutions for nonlinear fractional integrodifferential equations of Sobolev type with nonlocal conditions in Banach spaces. To illustrate our abstract results, an example is given.
MSC:35A05, 34G20, 34K05, 26A33.
1 Introduction
We are concerned with the nonlocal nonlinear fractional problem


where , is the Riemann-Liouville fractional derivative, , are real numbers, B and A are linear closed operators with domains contained in a Banach space X and ranges contained in a Banach space Y, , is a family of linear closed operators defined on dense sets respectively in X into X, and are given abstract functions. Here .
Fractional differential equations have attracted many authors [1, 6–8, 21, 24, 25, 30]. This is mostly because it efficiently describes many phenomena arising in engineering, physics, economics and science. In fact, we can find several applications in viscoelasticity, electrochemistry, electromagnetic, etc. For example, Machado [22] gave a novel method for the design of fractional order digital controllers.
Following Gelfand and Shilov [20], we define the fractional integral of order as
also, the (Riemann-Liouville) fractional derivative of the function f of order as
where f is an abstract continuous function on the interval and is the Gamma function, see also [14, 24].
The existence results to evolution equations with nonlocal conditions in a Banach space was studied first by Byszewski [9, 10]; subsequently, many authors were pointed to the same field, see for instance [2–4, 11–13, 19, 28].
Deng [15] indicated that using the nonlocal condition to describe, for instance, the diffusion phenomenon of a small amount of gas in a transparent tube can give a better result than using the usual local Cauchy problem . Let us observe also that since Deng’s papers, the function h is considered
where are given constants and .
However, among the previous research on nonlocal Cauchy problems, few authors have been concerned with mild solutions of fractional semilinear differential equations [23].
Recently, many authors have extended this work to various kinds of nonlinear evolution equations [2, 3, 5, 11, 12, 18]. Balachandran and Uchiyama [3] proved the existence of mild and strong solutions of a nonlinear integrodifferential equation of Sobolev type with nonlocal condition.
In this paper, motivated by [3, 13, 17, 19], we use Schauder fixed point theorem and the semigroup theory to investigate the existence and uniqueness of mild and strong solutions for nonlinear fractional integrodifferential equations of Sobolev type with nonlocal conditions in Banach spaces, the solutions were obtained by using Gelfand-Shilov approach in fractional calculus and are given in terms of some probability density functions such that their Laplace transforms are indicated [17].
Our paper is organized as follows. Section 2 is devoted to the review of some essential results. In Section 3, we state and prove our main results; the last section deals with giving an example to illustrate the abstract results.
2 Preliminary results
In this section, we mention some results obtained by Balachandran [3], El-Borai [19] and Pazy [26], which will be used to get our new results. Let X and Y be Banach spaces with norm and respectively. The operator satisfies the following hypotheses: (H1) = B is bijective,; (H2) = is compact.. The above fact and the closed graph theorem imply the boundedness of the linear operator . Further generates a uniformly continuous semigroup such that for every and all , see [29].
Let , and .
It is supposed that (H3) = f and g are continuous in t on I, Δ respectively, and there exist constants such that , for all , and ..
Definition 2.1 By a strong solution of the nonlocal Cauchy problem (1.1), (1.2), we mean a function u with values in X such that
-
(i)
u is a continuous function in and ,
-
(ii)
exists and is continuous on , , and u satisfies (1.1) on and (1.2).
Remark 2.1 Let us take in the considered problem B is the identity, the inhomogeneous part is equal to an abstract continuous function , and the nonlocal condition is reduced to the initial condition i.e.


According to El-Borai [17–19], we first apply the fractional integral on both sides of (2.1) and then using (2.2), we apply the Laplace transform on the new integral equations by considering a suitable one-sided stable probability density whose Laplace transform is given. Hence we can conclude that a solution of the problem (2.1)-(2.2) can be formally represented by
where is a probability density function defined on such that its Laplace transform is given by
For more details, we refer to Zhou et al.[27, 31], see also [14, 16].
Using Gelfand-Shilov principle [20], it is suitable to rewrite (1.1), (1.2) in the form
where is the Gamma function.
According to [17–19], the equation (2.4) is equivalent to the integral equation
where
It is assumed that there exists an operator ψ on given by the formula
satisfying and for
also (H4) = .. Further we assume (H5) = There is a number such that
where , , and is a positive constant, .; (H6) = The functions are uniformly Hölder continuous in for every element h in .. Suppose that is a -semigroup of operators on X such that , where δ is a positive constant and . Noting that (see [14], p.4]).
If , then , which achieves that ψ exists on X.
3 Main results
The following is different from [3, 19, 26] and represents the new result.
Lemma 3.1 If u is a continuous solution of (2.5), then u satisfies the integral equation
Proof Using (2.5) and (1.2), we get
Then
Thus
Hence the required result. □
Definition 3.1 A continuous solution of the integral equation (3.1) is called a mild solution of the nonlocal problem (1.1), (1.2) on I.
Theorem 3.2 If the assumptions (H1)∼(H4) hold and, then the problem (1.1), (1.2) has a mild solution on I.
Proof Let and . It is easy to see that is a bounded closed convex subset of Z. We define a mapping by
Noting also that (see [14], p.4]), we have
We deduce that φ is continuous and maps into itself. Moreover, φ maps into a precompact subset of . Note that the set is precompact in X, for every fixed . We shall show that is an equicontinuous family of functions. For , we have
The right-hand side of the above inequality is independent of and tends to zero as as a consequence of the continuity of and in the uniform operator topology for . It is clear that S is bounded in Z. Thus by Arzela-Ascoli’s theorem, S is precompact. Hence by the Schauder fixed point theorem, φ has a fixed point in and any fixed point of φ is a mild solution of (1.1), (1.2) on I such that for all . □
Theorem 3.3 Assume that
-
(i)
Conditions (H 1)∼(H 6) hold,
-
(ii)
Y is a reflexive Banach space with norm ,
-
(iii)
there are numbers and such that
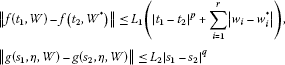
for all, and all, whereand.
Then the problem (1.1), (1.2) has a unique strong solution on I.
Proof Applying Theorem 3.2, the problem (1.1), (1.2) has a mild solution . Now, we shall show that u is a unique strong solution of the considered problem on I.
According to (H6), is uniformly Hölder continuous in for every element u in combined with (iii), which implies that and are uniformly Hölder continuous on I.
Set
From (3.1), the solution u of the considered problem can be written in the form
Noting that Ψ and ψ are bounded, using our assumptions, we observe that there exists a unique function which satisfies the equation
Also as in [19], p.409], we deduce that
for all and . It follows that for all . □
4 Example
Consider the nonlinear integro-partial differential equation of fractional order

with nonlocal condition
where , , , , , is an n-dimensional multi-index, , ,
and Ω is an open subset of . Let be the set of all square integrable functions on . We denote by the set of all continuous real-valued functions defined on which have continuous partial derivatives of order less than or equal to m. By we denote the set of all functions with compact supports. Let be the completion of with respect to the norm
It is supposed that
-
(i)
The operator is uniformly elliptic on . In other words, all the coefficients , are continuous and bounded on , and there is a positive number c such that
for all and all , , where , and .
(ii) All the coefficients , satisfy a uniform Hölder condition on . Under these conditions, the operator E with the domain of definition generates an analytic semigroup defined on , and it is well known that is dense in , see [17], p.438].
Lemma 4.1 The solution representation of (4.1), (4.2) can be written explicitly.
Proof Let be a family of deterministic square matrices of order k and let . We assume that
has roots which satisfy the inequality , for all and for any real vector σ, . If Θ is a matrix of order , then we introduce .
It is well known that there exists a fundamental matrix solution which satisfies the system

This fundamental matrix also satisfies the inequality
where and are positive constants. From [13], p.58], if the nonlocal function is an element in Hilbert space , then we can write
It can be proved that
where M is a positive constant, and .
([17]) The nonlocal Cauchy problems (4.1), (4.2) are equivalent to the integral equation
where the explicit form of Q is given by
. Applying Theorem 3.2, we achieve the proof of the existence of mild solutions of the problems (4.1), (4.2). In addition, if the operators F and G satisfy the following:
-
(iii)
There are numbers and such that
and
for all , , and all . Then applying Theorem 3.3, we deduce that (4.1), (4.2) has a unique strong solution. □
5 Conclusion
In this article, a new solution representation for Sobolev type fractional evolution equation has been proved using Deng’s nonlocal condition, a suitable explicit form of the semigroup has been discussed. Moreover, the existence result of mild solutions for nonlinear fractional integrodifferential equations of Sobolev type with nonlocal conditions in Banach spaces has been established by using Arzela-Ascoli’s theorem and Schauder fixed point theorem. Further, the uniformly Hölder continuous condition has been applied for the existence of strong solution.
References
Agarwal RP, Lakshmikanthama V, Nieto JJ: On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. 2010, 72: 2859-2862. 10.1016/j.na.2009.11.029
Ahmad B, Nieto JJ: Existence of solutions for nonlocal boundary value problems of higher order nonlinear fractional differential equations. Abstr. Appl. Anal. 2009., 2009:
Balachandran K, Uchiyama K: Existence of solutions of nonlinear integrodifferential equations of Sobolev type with nonlocal condition in Banach spaces. Proc. Indian Acad. Sci. Math. Sci. 2000, 110(2):225-232. 10.1007/BF02829493
Balachandran K, Samuel FP: Existence of solutions for quasilinear delay integrodifferential equations with nonlocal conditions. Electron. J. Differ. Equ. 2009, 2009(6):1-7.
Balachandran K, Kumar RR: Existence of solutions of integrodifferential evolution equations with time varying delays. Appl. Math. E-Notes 2007, 7: 1-8.
Baleanu D, Mustafa OG: On the global existence of solutions to a class of fractional differential equations. Comput. Math. Appl. 2010, 59(5):1835-1841. 10.1016/j.camwa.2009.08.028
Baleanu D, Mustafa OG, Agarwal RP: Asymptotically linear solutions for some linear fractional differential equations. Abstr. Appl. Anal. 2010., 2010:
Belmekki M, Benchohra M: Existence results for fractional order semilinear functional differential equations with nondense domain. Nonlinear Anal. 2010, 72: 925-932. 10.1016/j.na.2009.07.034
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. J. Math. Anal. Appl. 1991, 162: 494-505. 10.1016/0022-247X(91)90164-U
Byszewski L: Applications of properties of the right hand sides of evolution equations to an investigation of nonlocal evolution problems. Nonlinear Anal. 1998, 33: 413-426. 10.1016/S0362-546X(97)00594-4
Debbouche A, Baleanu D: Controllability of fractional evolution nonlocal impulsive quasilinear delay integro-differential systems. Comput. Math. Appl. 2011, 62: 1442-1450. 10.1016/j.camwa.2011.03.075
Debbouche A: Fractional nonlocal impulsive quasilinear multi-delay integro-differential systems. Adv. Differ. Equ. 2011, 5: 1-10.
Debbouche A: Fractional evolution integro-differential systems with nonlocal conditions. Adv. Dyn. Syst. Appl. 2010, 5(1):49-60.
Debbouche A, El-Borai MM: Weak almost periodic and optimal mild solutions of fractional evolution equations. Electron. J. Differ. Equ. 2009, 2009(46):1-8.
Deng K: Exponential decay of solutions of semilinear parabolic equations with nonlocal initial conditions. J. Math. Anal. Appl. 1993, 179: 630-637. 10.1006/jmaa.1993.1373
El-Borai MM, Debbouche A: On some fractional integro-differential equations with analytic semigroups. Int. J. Contemp. Math. Sci. 2009, 4(28):1361-1371.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos Solitons Fractals 2002, 14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: Semigroups and some nonlinear fractional differential equations. Appl. Math. Comput. 2004, 149(3):823-831. 10.1016/S0096-3003(03)00188-7
El-Borai MM: On some fractional evolution equations with nonlocal conditions. Int. J. Pure Appl. Math. 2005, 24(3):405-413.
Gelfand IM, Shilov GE: Generalized Functions. Nauka, Moscow; 1959.
Li F: Mild solutions for fractional differential equations with nonlocal conditions. Adv. Differ. Equ. 2010., 2010:
Machado JAT: Analysis and design of fractional-order digital control systems. Syst. Anal. Model. Simul. 1997, 27(2-3):107-122.
Mophou GM, N’Guerekata GM: Mild solutions for semilinear fractional differential equations. Electron. J. Differ. Equ. 2009, 2009(21):1-9.
Podlubny I: Fractional Differential Equations. Academic Press, San Diego; 1999.
Tatar N-E: On a boundary controller of fractional type. Nonlinear Anal. 2010, 72: 3209-3215. 10.1016/j.na.2009.12.017
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, Berlin; 1983.
Wang JR, Zhou Y: A class of fractional evolution equations and optimal controls. Nonlinear Anal., Real World Appl. 2011, 12: 262-272. 10.1016/j.nonrwa.2010.06.013
Yan Z: Controllability of semilinear integrodifferential systems with nonlocal conditions. Int. J. Comput. Appl. Math. 2007, 3(2):221-236.
Zaidman S: Abstract Differential Equations. Pitman, London; 1979.
Zhao Y, Sun S, Han Z, Li Q: Positive solutions to boundary value problems of nonlinear fractional differential equations. Abstr. Appl. Anal. 2011., 2011:
Zhou Y, Jiao F: Nonlocal Cauchy problem for fractional evolution equations. Nonlinear Anal., Real World Appl. 2010, 11: 4465-4475. 10.1016/j.nonrwa.2010.05.029
Acknowledgements
The authors would like to thank the referees for their valuable comments and remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AD wrote the first draft, DB corrected and improved it and RPA prepared the final version. All authors read and approved the final draft.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Debbouche, A., Baleanu, D. & Agarwal, R.P. Nonlocal nonlinear integrodifferential equations of fractional orders. Bound Value Probl 2012, 78 (2012). https://doi.org/10.1186/1687-2770-2012-78
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-78