Asymptotic analysis for reaction-diffusion equations with absorption

Abstract

In this paper, we study the blow-up and nonextinction phenomenon of reaction-diffusion equations with absorption under the null Dirichlet boundary condition. We at first discuss the existence and nonexistence of global solutions to the problem, and then give the blow-up rate estimates for the nonglobal solutions. In addition, the nonextinction of solutions is also concerned.

MSC:35B33, 35K55, 35K60.

1 Introduction

In this paper, we consider the reaction-diffusion equations with absorption

(1.1)

where $m>1$, $p>0$, $q\ge 1$, $p\ne q$, $\mathrm{\Omega }\subset {\mathbb{R}}^N$ is a bounded domain with smooth boundary ∂ Ω, and $u_0(x)$ is a nontrivial, nonnegative, bounded, and appropriately smooth function. Parabolic equations like (1.1) appear in population dynamics, chemical reactions, heat transfer, and so on. We refer to [2, 8, 9] for details on physical models involving more general reaction-diffusion equations.

The semilinear case ($m=1$) of (1.1) has been investigated by Bedjaoui and Souplet [3]. They obtained that the solutions exist globally if either $p<max\{q,1\}$ or $p=max\{q,1\}$, and the solutions may blow up in finite time for large initial value if $p>max\{q,1\}$. Recently, Xiang et al. [11] considered the blow-up rate estimates for nonglobal solutions of (1.1) ($m=1$) with $p>max\{q,1\}$, and obtained that (i) ${max}_{\mathrm{\Omega }}u(x,t)\ge c{(T-t)}^{-\frac{1}{p-1}}$; (ii) ${max}_{\mathrm{\Omega }}u(x,t)\le C{(T-t)}^{-\frac{1}{p-1}}$ if $p\le 1+\frac{2}{N+1}$, where $c,C>0$ are positive constants. Liu et al. [7] studied the extinction phenomenon of solutions of (1.1) for the case $0<m<1$ with $q=1$ and obtained some sufficient conditions about the extinction in finite time and decay estimates of solutions in $\mathrm{\Omega }\subset {\mathbb{R}}^N$ ($N>2$).

Recently, Zhou et al. [10] investigated positive solutions of the degenerate parabolic equation not in divergence form

(1.2)

where $p\ge 1$, $q,a,b>0$, $r>1$. They at first gave some conditions about the existence and nonexistence of global solutions to (1.2), and then studied the large time behavior for the global solutions.

Motivated by the above mentioned works, the aim of this paper is threefold. First, we determine optimal conditions for the existence and nonexistence of global solutions to (1.1). Secondly, by using the scaling arguments we establish the exact blow-up rate estimates for solutions which blow up in a finite time. Finally, we prove that every solution to (1.1) is nonextinction.

As it is well known that degenerate equations need not possess classical solutions, we give a precise definition of a weak solution to (1.1).

Definition 1.1 Let $T>0$ and $Q_T=\mathrm{\Omega }\times (0,T)$, $E=\{u\in L^{2p}(Q_T)\cap L^{2q}(Q_T);u_t,\mathrm{\nabla }u\in L^2(Q_T)\}$, $E_0=\{u\in E;u=0\text{ on }\partial \mathrm{\Omega }\}$, a nonnegative function $u(x,t)\in E$ is called a weak upper (or lower) solution to (1.1) in $Q_T$ if for any nonnegative function $\phi \in E_0$, one has

In particular, $u(x,t)$ is called a weak solution of (1.1) if it is both a weak upper and a weak lower solution. For every $T<\mathrm{\infty }$, if $u(x,t)$ is a weak solution of (1.1) in $Q_T$, we say that $u(x,t)$ is global. The local in time existence of nonnegative weak solutions have been established (see the survey [1]), and the weak comparison principle is stated and proved in the Appendix in this paper.

The behavior of the weak solutions is determined by the interactions among the multinonlinear mechanisms in the nonlinear diffusion equations in (1.1). We divide the $(m,p,q)$-parameter region into three classes: (i) $p<max\{m,q\}$; (ii) $p=max\{m,q\}$; (iii) $p>max\{m,q\}$.

Theorem 1.1 If $p<max\{m,q\}$, then all solutions of (1.1) are bounded.

Let $\varphi (x)$ be the first eigenfunction of

$$-\mathrm{\Delta }\varphi (x)=\lambda \varphi (x)\text{in }\mathrm{\Omega },\varphi (x)=0\text{in }\partial \mathrm{\Omega }$$

(1.3)

with the first eigenvalue ${\lambda }_1$, normalized by ${\parallel \varphi \parallel }_{\mathrm{\infty }}=1$, then ${\lambda }_1>0$ and $\varphi >0$ in Ω.

Theorem 1.2 Assume that $p=max\{m,q\}$. Then all solutions are global if ${\lambda }_1\ge 1$, and there exist both global and nonglobal solutions if ${\lambda }_1<1$.

Theorem 1.3 If $p>max\{m,q\}$, then there exist both global and nonglobal solutions to (1.1).

To obtain the blow-up rate of blow-up solutions to (1.1), we need an extra assumption that $\mathrm{\Omega }=B_R(0)=\{x\in {\mathbb{R}}^N:|x|<R\}$ and $u_0=u_0(r)$, $u_0^{\prime }(r)\le 0$, here $r=|x|$. By the assumption and comparison principle, we know that u is radially decreasing in r with ${max}_{\mathrm{\Omega }}u(x,t)=u(0,t)$.

Theorem 1.4 Suppose that $p>max\{m,q\}$. If the solution $u(x,t)$ of (1.1) blows up in finite time T, then there exists a positive constant c such that

$$\underset{\mathrm{\Omega }}{max}u(x,t)\ge c{(T-t)}^{-\frac{1}{p-1}}\mathit{\text{as}}t\to T.$$

Furthermore, if $p>m\ge q$, then we have also the upper estimate, that is, there exists a positive constant C such that

$$\underset{\mathrm{\Omega }}{max}u(x,t)\le C{(T-t)}^{-\frac{1}{p-1}}\mathit{\text{as}}t\to T.$$

We remark that in $\mathrm{\Omega }={\mathbb{R}}^N$, Liang [6] studied the blow up rate of blow-up solutions to the following Cauchy problem

$$u_t=\mathrm{\Delta }{u}^m+u^p,(x,t)\in {\mathbb{R}}^N\times (0,T)$$

(1.4)

with the bounded initial function, $1<m<p<m\frac{N+2}{{(N-2)}_{+}}$, and obtained that ${\parallel u\parallel }_{L^{\mathrm{\infty }}({\mathbb{R}}^N)}<C{(T-t)}^{-\frac{1}{p-1}}$ for $t\in (0,T)$. By using the same scaling arguments in this paper, we can find that Theorem 1.4 is correct for (1.4) with $p>m$.

Now, we pay attention to the nonextinction property of solutions and have the following result.

Theorem 1.5 Any solution of (1.1) does not go extinct in finite time for any nontrivial and nonnegative initial value $u_0(x)$ with $meas\{x\in \mathrm{\Omega };u_0(x)>0\}>0$.

The rest of this paper is organized as follows. In the next section, we discuss the global existence and nonexistence of solutions, and prove Theorems 1.1-1.3. Subsequently, in Sects. 3 and 4, we consider the estimate of the blow-up rate and study the nonextinction phenomenon for the problem (1.1). The weak comparison principle is stated and proved in the Appendix.

2 Global existence and nonexistence

Proof of Theorem 1.1 If $m\ge q$, that is $p<m$, then by the comparison principle, we have $u\le w$, where w satisfies

(2.1)

We know from [4, 5] that w is bounded.

If $m<q$, we have $p<q$. It is obvious that $\overline{u}=max\{1,{\parallel u_0\parallel }_{\mathrm{\infty }}\}$ is a time-independent upper solution to (1.1). □

Proof of Theorem 1.2 Since $p\ne q$ and $p=max\{m,q\}$ imply $p=m>q$. Due to the fact that the solution of (2.1) is an upper solution of (1.1), the conclusions for ${\lambda }_1\ge 1$ is obvious true; see [4, 5].

Now consider ${\lambda }_1<1$ with small initial data. Let $\psi (x)$ be the unique solution of

$$-\mathrm{\Delta }\psi (x)=1\text{in }\mathrm{\Omega },\psi (x)=0\text{on }\partial \mathrm{\Omega },$$

(2.2)

and $h(t)$ solves $h^{\prime }(t)=-\delta h{(t)}^m$ with $h(0)=h_0$, where $0<\delta \le {\parallel \psi \parallel }_{\mathrm{\infty }}^{-\frac{1}{m}}$. Set $\overline{u}=h(t){\psi }^{\frac{1}{m}}(x)$. Then

$$\begin{array}{rcl}{\overline{u}}_t-\mathrm{\Delta }{\overline{u}}^m-{\overline{u}}^m+{\overline{u}}^q& =& -\delta h^m{\psi }^{\frac{1}{m}}+h^m-h^m\psi +h^q{\psi }^{\frac{q}{m}}\\ =& h^m(1-\delta {\psi }^{\frac{1}{m}})+h^q{\psi }^{\frac{q}{m}}(1-h^{m-q}{\psi }^{\frac{m-q}{m}})\ge 0\end{array}$$

provided $h_0^{m-q}{\psi }^{\frac{m-q}{m}}\le 1$. Thus, $\overline{u}$ is an upper solution of (1.1), and consequently, $u\le \overline{u}=h(t){\psi }^{\frac{1}{m}}(x)\to 0$ as $t\to \mathrm{\infty }$.

If ${\lambda }_1<1$ with large initial data, we first introduce some transformations. Let $v=u^m$ and $\tau =mt$, then (1.1) becomes the following equations not in divergence form:

where $r=\frac{m-1}{m}$, $s=\frac{q}{m}<1$ and $v_0(x)=u_0^m(x)$.

Let $J(\tau )=\frac{1}{1-r}{\int }_{\mathrm{\Omega }}{v}^{1-r}\varphi dx$, where ϕ is given in (1.3). Then we have

$$\begin{array}{rcl}{J}^{\prime }(\tau )& =& {\int }_{\mathrm{\Omega }}(\mathrm{\Delta }v+v-v^s)\varphi (x)dx\\ =& (1-{\lambda }_1){\int }_{\mathrm{\Omega }}v\varphi dx-{\int }_{\mathrm{\Omega }}{v}^s\varphi dx.\end{array}$$

(2.3)

By using Hölder’s inequality, we discover

$${\int }_{\mathrm{\Omega }}{v}^s\varphi dx\le {\left({\int }_{\mathrm{\Omega }}v\varphi dx\right)}^s{\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^{1-s}$$

(2.4)

and

$${\int }_{\mathrm{\Omega }}{v}^{1-r}\varphi dx\le {\left({\int }_{\mathrm{\Omega }}v\varphi dx\right)}^{1-r}{\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^r$$

i.e.,

$${\int }_{\mathrm{\Omega }}v\varphi dx\ge {[(1-r)J(\tau ){\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^{-r}]}^{\frac{1}{1-r}}.$$

(2.5)

Inserting (2.4) into (2.3), we have

$$\begin{array}{rcl}{J}^{\prime }(\tau )& \ge & (1-{\lambda }_1){\int }_{\mathrm{\Omega }}v\varphi dx-{\left({\int }_{\mathrm{\Omega }}v\varphi dx\right)}^s{\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^{1-s}\\ =& {\left({\int }_{\mathrm{\Omega }}v\varphi dx\right)}^s[(1-{\lambda }_1){\left({\int }_{\mathrm{\Omega }}v\varphi dx\right)}^{1-s}-{\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^{1-s}].\end{array}$$

(2.6)

According to (2.5), (2.6), we obtain

$$J^{\prime }(\tau )\ge \frac{(1-{\lambda }_1)}{2}{[(1-r){\left({\int }_{\mathrm{\Omega }}\varphi dx\right)}^{-r}]}^{\frac{1}{1-r}}J{(\tau )}^{\frac{1}{1-r}}$$

(2.7)

as long as

$$J(\tau )\ge \frac{1}{1-r}{\left(\frac{2}{1-{\lambda }_1}\right)}^{\frac{1-r}{1-s}}\left({\int }_{\mathrm{\Omega }}\varphi dx\right).$$

Hence, if $u_0$ satisfies

$$J(0)\ge \frac{1}{1-r}{\left(\frac{2}{1-{\lambda }_1}\right)}^{\frac{1-r}{1-s}}\left({\int }_{\mathrm{\Omega }}\varphi dx\right),$$

we then follow from (2.7) that $J(\tau )$, and consequently $u(x,t)$, blows up in finite time since $J(\tau )$ is increasing and $\frac{1}{1-r}=m>1$. □

Proof of Theorem 1.3 Let $h(t)$ solves $h^{\prime }(t)=-h{(t)}^p$ with $h(0)=h_0$, and set $\overline{u}=h(t){\psi }^{\frac{1}{m}}(x)$, where ψ is defined in (2.2). Then

$$\begin{array}{rcl}{\overline{u}}_t-\mathrm{\Delta }{\overline{u}}^m-{\overline{u}}^p+{\overline{u}}^q& =& -h^p{\psi }^{\frac{1}{m}}+h^m-h^p{\psi }^{\frac{p}{m}}+h^q{\psi }^{\frac{q}{m}}\\ =& h^m(1-h^{p-m}{\psi }^{\frac{1}{m}})+h^q{\psi }^{\frac{q}{m}}(1-h^{p-q}{\psi }^{\frac{p-q}{m}}).\end{array}$$

Since $p>max\{m,q\}$, we can choose $h_0$ small enough such that ${\overline{u}}_t-\mathrm{\Delta }{\overline{u}}^m-{\overline{u}}^p+{\overline{u}}^q\ge 0$. Thus, $\overline{u}$ is an upper solution of (1.1) provided $u_0(x)\le h_0{\psi }^{\frac{1}{m}}(x)$, and consequently, $u\le \overline{u}=h(t){\psi }^{\frac{1}{m}}(x)\to 0$ as $t\to \mathrm{\infty }$.

Now deal with the nonexistence of global solutions, we seek a blow-up self-similar lower solution of the problem (1.1). Without loss of generality, we may assume that Ω contains the origin. Since $p>max\{m,q\}$, we can choose constant α such that

$$\frac{1}{p-1}<\alpha <min\{\frac{1}{m-1},\frac{1}{q-1}\},$$

and consider the function

$$\underline{u}(x,t)={(T-t)}^{-\alpha }f(\xi ),\xi =\frac{|x|}{{(T-t)}^{\beta }},\beta =\frac{1-(m-1)\alpha }{2},$$

(2.8)

where $f(\xi )={(a^2-{\xi }^2)}_{+}^{\frac{1}{m-1}}$. Note that the support of $\underline{u}(x,t)$ is contained in $B(0,a{T}^{\beta })$, which is included in Ω if T is sufficiently small.

After some computations, we have

It will be obtained from the above equalities that

$${\underline{u}}_t-\mathrm{\Delta }{\underline{u}}^m-{\underline{u}}^p+{\underline{u}}^q\le 0,\text{in }\mathrm{\Omega }\times (0,T),$$

if $f(\xi )$ satisfies

(2.9)

It is easy to see that

To satisfy (2.9), we distinguish the two zones $0<\xi \le \theta a$ and $\theta a<\xi <a$, where

$$\theta =\sqrt{\frac{\alpha +\frac{2mN}{m-1}}{\alpha +\frac{2mN}{m-1}+\frac{4m}{{(m-1)}^2}}}<1.$$

(2.10)

For $\theta a<\xi <a$, we have

then

For $0<\xi \le \theta a$, we have $f(\xi )\ge {(1-{\theta }^2)}^{\frac{1}{m-1}}{a}^{\frac{2}{m-1}}>0$. It follow from $p\alpha >\alpha +1>q\alpha$ that (2.9) is satisfied for $0<\xi \le \theta a$, $\theta a<\xi <a$ if T is sufficiently small. Therefore, $\underline{u}$ given by (2.8) is a blow-up lower solution of the problem (1.1) with appropriately large $u_0$. And consequently, there exist nonglobal solutions to (1.1). □

3 Blow-up rate

In this section, we study the speeds at which the solutions to (1.1) blow up. Assume that $\mathrm{\Omega }=B_R(0)=\{x\in {\mathbb{R}}^N:|x|<R\}$ and $u_0=u_0(r)$, $u_0^{\prime }(r)\le 0$, here $r=|x|$. Then we know from the assumption and comparison principle that u is radially decreasing in r with ${max}_{\mathrm{\Omega }}u(x,t)=u(0,t)$. In this section, denote by T the blow-up time for the nonglobal solutions to (1.1).

Proof of Theorem 1.4 Fix $t\in (0,T)$ such that $M(t)={max}_{\mathrm{\Omega }}u(x,t)\ge 1$, and let

$$a=M^{-\frac{p-m}{2}},b=M^{1-p},$$

and define the function ${\psi }_M(y,s)=\frac{1}{M(t)}u(ay,bs+t)$ in $B_{M^{\frac{p-m}{2}}R}(0)\times (0,S)$, where $S=M^{p-1}(T-t)$. ${\psi }_M$ blows up at $s=S$, moreover, it is a solution of the following problem:

(3.1)

We now construct an upper solution for this problem. Set

$$\overline{w}(y,s)={(S_1-s)}^{-\alpha }{(L+\delta {(L-\xi )}_{+})}^{\frac{1}{m-1}},\xi =|y|{(S_1-s)}^{-\beta },$$

where $\alpha =\frac{1}{p-1}$, $\beta =\frac{p-m}{2(p-1)}$, and

$$0<L<{\alpha }^{\frac{m-1}{p-1}}{2}^{-\frac{p+2m-3}{p-1}},S_1^{-\alpha }{L}^{\frac{1}{m-1}}>1,0<\delta <min\{1,\frac{(m-1)\alpha }{4\beta },\frac{m-1}{2}\sqrt{\frac{\alpha L}{m}}\}.$$

After a direct computation, for $0<\xi <L$, we have

Then

Clearly, ${\overline{w}}_s-\mathrm{\Delta }{\overline{w}}^m-{\overline{w}}^p+M^{q-p}{\overline{w}}^q\ge 0$ for $\xi >L$, and $\overline{w}(y,s)>0$ on $\partial B_{M^{\frac{p-m}{2}}R}(0)\times (0,S_1)$, $\overline{w}(y,0)\ge {\psi }_M(y,0)$ in $B_{M^{\frac{p-m}{2}}R}(0)$. We have an upper solution independent of M, for all M large enough. Therefore, the blow-up time of ${\psi }_M$ is greater than $S_1$, that is $M^{p-1}(T-t)\ge S_1$. This implies

$$\underset{\mathrm{\Omega }}{max}u(x,t)\ge c{(T-t)}^{-\frac{1}{p-1}},$$

and the lower estimate is obtained.

In order to obtained the upper estimates for the blow-up rate, we look for a lower solution to (3.1) with $M(t)>M_0$. Set

$$\underline{w}(y,s)={(S_2-s)}^{-\alpha }f(\xi ),\xi =\frac{|y|}{{(S_2-s)}^{\beta }},$$

where $\alpha =\frac{1}{p-1}$, $\beta =\frac{p-m}{2(p-1)}$, $f(\xi )={(a^2-{\xi }^2)}_{+}^{\frac{1}{m-1}}$, $a^{\frac{2(p-1)}{m-1}}>{(1-{\theta }^2)}^{\frac{1-p}{m-1}}(\alpha +\frac{2mN}{m-1})$ and θ is given in (2.10). Let $M_0$ satisfies

$$\begin{array}{rcl}{M}_0& \ge & max\{{\left(\frac{m-1}{2\beta }{\theta }^{-2}{S}_2^{(p-q)\alpha }{a}^{\frac{2(q-1)}{m-1}}\right)}^{\frac{1}{p-q}},{\left(a{S}_2^{\beta }{R}^{-1}\right)}^{\frac{2}{p-m}},{\left(\frac{2}{\mu }{S}_2^{-(q-1)\alpha }{a}^{\frac{2(q-1)}{m-1}}\right)}^{\frac{1}{p-q}},\\ {\left({({(1-{\theta }^2)}^{\frac{p-1}{m-1}}{a}^{\frac{2(p-1)}{m-1}}-(\alpha +\frac{2mN}{m-1}))}^{-1}{S}_2^{(p-q)\alpha }{a}^{\frac{2(q-1)}{m-1}}\right)}^{\frac{1}{p-q}}\},\end{array}$$

where $S_2$, μ are to be determined later. Clearly, $\underline{w}(y,s)=0$ on $\partial B_{M^{\frac{p-m}{2}}R}(0)\times (0,S)$. As the same arguments in the proof of Theorem 1.3, we have for $\theta a\le \xi <a$ that

For $0<\xi \le \theta a$, we have that

Now, in order to deal with the initial data, consider the function

$$z(y,s)=S_2^{-\alpha }{(a^2-\frac{{|y|}^2}{S_2^{2\beta }}{s}^{-\lambda })}_{+}^{\frac{1}{m-1}}{s}^{-\mu },$$

where $\lambda =\frac{1}{(m-1)N+1}$, $\mu =\frac{1-\lambda }{m-1}$, and $S_2=\frac{4m}{(m-1)\lambda }$.

After a direct computation, we have

Then

Furthermore, $z(y,s)=0$ on $\partial B_{M^{\frac{p-m}{2}}R}(0)\times (0,1)$. In addition, $z(y,0)={lim}_{s\to 0}z(y,s)=0$ a.e. in $B_{M^{\frac{p-m}{2}}R}(0)$. Therefore, by the comparison principle, we have that ${\psi }_M(y,s)\ge z(y,s)$ for $0\le s\le 1$. By the virtue of $\underline{w}(y,0)=z(y,1)$, we have ${\psi }_M(y,s+1)\ge \underline{w}(y,s)$.

We have a lower solution independent of M, for all $M>M_0$. Therefore, the blow-up time of ${\psi }_M$ is less than $S_2+1$, that is $M^{p-1}(T-t)\le S_2+1$. This implies

$$\underset{\mathrm{\Omega }}{max}u(x,t)\le C{(T-t)}^{-\frac{1}{p-1}},$$

and the upper estimate is obtained. □

4 Nonextinction

We discuss the nonextinction of the solution to the problem (1.1) in this section. For $p<1$, the uniqueness of the weak solution to (1.1) may not hold. In this case, we only consider the maximal solution, which can be obtained by standard regularized approximation methods. Clearly, the comparison principle is valid for the maximal solution.

Proof of Theorem 1.5 For $meas\{x\in \mathrm{\Omega };u_0(x)>0\}>0$, there exists a region ${\mathrm{\Omega }}_0\subset \mathrm{\Omega }$ and $ϵ\in (0,1)$ such that $u_0(x)\ge ϵ$ a.e. in ${\mathrm{\Omega }}_0$. ${\lambda }_0$ is the first Dirichlet eigenvalue of −Δ on ${\mathrm{\Omega }}_0$ with corresponding eigenfunction ${\varphi }_0(x)$, normalized by ${\parallel {\varphi }_0\parallel }_{\mathrm{\infty }}=1$, and prolong solution ${\varphi }_0$ by 0 in $\mathrm{\Omega }\setminus {\mathrm{\Omega }}_0$. We treat the five subcases for the proof.

• (a) For $p\le 1$, set $\underline{u}=h(t){\varphi }_0^{\frac{1}{m}}$, where

  

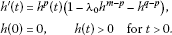
Then

By the comparison principle, we have $u\ge \underline{u}>0$ in ${\mathrm{\Omega }}_0$.

• (b) For $p>1$, $1\le q\le m$, we let $\underline{u}=h(t){\varphi }_0^{\frac{1}{m}}$, $h^{\prime }(t)=-(1+{\lambda }_0)h^q(t)$ with $h(0)=h_0<ϵ$. Then

  $$\begin{array}{rcl}{\underline{u}}_t-\mathrm{\Delta }{\underline{u}}^m-{\underline{u}}^p+{\underline{u}}^q& \le & -(1+{\lambda }_0)h^q(t){\varphi }_0^{\frac{1}{m}}+{\lambda }_0{h}^m{\varphi }_0+h^q{\varphi }_0^{\frac{q}{m}}\\ =& -h^q(t){\varphi }_0^{\frac{1}{m}}(1+{\lambda }_0-{\lambda }_0{h}^{m-q}{\varphi }_0^{\frac{m-q}{m}}-{\varphi }_0^{\frac{q-1}{m}})\\ \le & 0.\end{array}$$

Then we know by the comparison principle that $u\ge \underline{u}>0$ in ${\mathrm{\Omega }}_0$.

• (c) For $1<p<m$, $q>m$, we let $\underline{u}=h(t){\varphi }_0^{\frac{1}{m}}$, and

  

where $\delta <min\{ϵ,{(\frac{1}{1+{\lambda }_0})}^{\frac{1}{m-p}}\}$. It is easy to see that $h(t)$ is nonincreasing and $h(t)\to M^{\frac{1}{p-m}}$ as $t\to \mathrm{\infty }$.

$$\begin{array}{rcl}{\underline{u}}_t-\mathrm{\Delta }{\underline{u}}^m-{\underline{u}}^p+{\underline{u}}^q& =& h^p(t)(1-M{h}^{m-p}){\varphi }_0^{\frac{1}{m}}+{\lambda }_0{h}^m{\varphi }_0(x)-h^p{\varphi }_0^{\frac{p}{m}}+h^q{\varphi }_0^{\frac{q}{m}}\\ =& -h^m{\varphi }_0^{\frac{1}{m}}(M-{\lambda }_0{\varphi }_0^{\frac{m-1}{m}}-h^{q-m}{\varphi }_0^{\frac{q-1}{m}})+h^p{\varphi }_0^{\frac{1}{m}}(1-{\varphi }_0^{\frac{p-1}{m}})\\ \le & -h^m{\varphi }_0^{\frac{1}{m}}(M-(1+{\lambda }_0){\varphi }_0^{\frac{p-1}{m}})+h^p{\varphi }_0^{\frac{1}{m}}(1-{\varphi }_0^{\frac{p-1}{m}})\\ \le & 0.\end{array}$$

And consequently, $u\ge \underline{u}>0$ in ${\mathrm{\Omega }}_0$.

• (d) For $p=m$, $q>m$, we let $\underline{u}=h(t){\varphi }_0^{\frac{1}{m}}$, where

  

Obviously, $h(t)$ is nonincreasing and $h(t)\to 0$ as $t\to \mathrm{\infty }$.

$$\begin{array}{rcl}{\underline{u}}_t-\mathrm{\Delta }{\underline{u}}^m-{\underline{u}}^p+{\underline{u}}^q& =& -(1+{\lambda }_0)h^m{\varphi }_0^{\frac{1}{m}}+{\lambda }_0{h}^m{\varphi }_0-h^p{\varphi }_0^{\frac{p}{m}}+h^q{\varphi }_0^{\frac{q}{m}}\\ \le & -h^m{\varphi }_0^{\frac{1}{m}}(1+{\lambda }_0-{\lambda }_0{\varphi }_0^{\frac{m-1}{m}}-h^{q-m}{\varphi }_0^{\frac{q-1}{m}})\\ \le & 0.\end{array}$$

Thus, we have $u\ge \underline{u}>0$ in ${\mathrm{\Omega }}_0$.

• (e) For $p>m$, $q>m$, we let $\underline{u}=h(t){\varphi }_0^{\frac{1}{m}}$, and

  

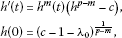
where c satisfies $1+{\lambda }_0<c<1+{\lambda }_0+{ϵ}^{p-m}$. It is easy to see that $h(t)$ is nonincreasing and $h(t)\to 0$ as $t\to \mathrm{\infty }$.

$$\begin{array}{rcl}{\underline{u}}_t-\mathrm{\Delta }{\underline{u}}^m-{\underline{u}}^p+{\underline{u}}^q& =& h^m(t)(h^{p-m}-c){\varphi }_0^{\frac{1}{m}}+{\lambda }_0{h}^m{\varphi }_0-h^p{\varphi }_0^{\frac{p}{m}}(x)+h^q{\varphi }_0^{\frac{q}{m}}\\ =& h^p{\varphi }_0^{\frac{1}{m}}(1-{\varphi }_0^{\frac{p-1}{m}})+h^m(t){\varphi }_0^{\frac{1}{m}}({\lambda }_0{\varphi }_0^{\frac{m-1}{m}}+h^{q-m}{\varphi }_0^{\frac{q-1}{m}}-c)\\ \le & h^p{\varphi }_0^{\frac{1}{m}}+h^m(t){\varphi }_0^{\frac{1}{m}}(1+{\lambda }_0-c)\\ \le & 0.\end{array}$$

By the comparison principle, we have $u\ge \underline{u}>0$ in ${\mathrm{\Omega }}_0$.

 □

Appendix

Theorem A.1 (Comparison principle)

Let $\underline{u}$ and $\overline{u}$ are a weak lower and a weak upper solutions of (1.1) in $Q_T$. If $p\ge 1$ or $\overline{u}$ has a positive lower bound, then $\underline{u}\le \overline{u}$ a.e. in $Q_T$.

Proof From the definition of weak upper and lower solutions, for any $0\le \phi \in E_0$, we obtain

Let $Q_t=\mathrm{\Omega }\times (0,t)$ for $t\in (0,T)$. Choose $\phi ={\chi }_{[0,t]}{(\underline{u}-\overline{u})}_{+}$, where ${\chi }_{[0,t]}$ is the characteristic function defined on $[0,t]$, Then we arrive at

By a simple calculation, we have

(A.1)

Noticing

we get

(A.2)

where L is a positive constant. By (A.1), (A.2), we have

$${\int }_{\mathrm{\Omega }}{(\underline{u}-\overline{u})}_{+}^{2}dx\le 2L\int {\int }_{Q_t}{(\underline{u}-\overline{u})}_{+}^{2}dxd\tau .$$

It follows immediately by using the Gronwall’s inequality that

$${\int }_{\mathrm{\Omega }}{(\underline{u}-\overline{u})}_{+}^{2}dx=0,$$

for almost all $t\in (0,T)$, and hence $\underline{u}\le \overline{u}$ a.e. in $\mathrm{\Omega }\times (0,T)$. □