- Research
- Open access
- Published:
On decay properties of solutions for degenerate Kirchhoff equations with strong damping and source terms
Boundary Value Problems volume 2012, Article number: 93 (2012)
Abstract
We investigate the degenerate Kirchhoff equations with strong damping and source terms of the form
in a bounded domain. We obtain the optimal decay rate for by deriving its decay estimate from below, provided that either ε is suitably small or the initial data satisfy the proper smallness assumption. The key ingredient in the proof is based on the work of Ono (J. Math. Anal. Appl. 381(1):229-239, 2011), with necessary modification imposed by our problem.
MSC:35L70, 35L80.
1 Introduction
In this paper, we consider the initial boundary value problem for the following degenerate Kirchhoff equations with strong damping and source terms:



where Ω is a bounded domain in () with a smooth boundary ∂ Ω. Here, and are positive constants and is a nonlinear term like , .
In the case , the nonlinear vibrations of the elastic string are written in the form:
for , ; where u is the lateral deflection, x the space coordinate, t the time, E the Young modulus, ρ the mass density, h the cross section area, L the length, the initial axial tension and f the external force. The equation was first introduced by Kirchhoff [1] in the study of stretched strings and plates, and is called the wave equation of Kirchhoff type after his name. Moreover, it is said that (1.4) is degenerate if and nondegenerate if .
A number of results on the solutions to problem (1.1)-(1.3) have been established by many authors. For example, Hosoya and Yamada [2] studied the following equation:
with (the nondegenerate case). They proved the global existence of a unique solution under the small data condition in . Similarly, in the degenerate case (), Nishihara and Yamada [3] obtained the global existence of solutions for small initial data in .
Concerning decay properties of solutions, Nakao [4] has derived decay estimates from above of solutions when in (1.1). Later, Nishihara [5] established a decay estimate from below of the potential of solutions to problem (1.1) without imposing . Nishihara and Ono [6–8] studied detailed cases of nondegenerate type and degenerate type to problem (1.1)-(1.3). They proved the existence and uniqueness of a global solution for initial data and the polynomial decay of the solution. Recently, in the absence of in (1.1), Ono [9] proved the optimal decay estimate for . And the decay property of the norm for was also given in that paper.
Motivated by these works, in this paper, we intend to give the optimal decay estimate for to problem (1.1)-(1.3). In this way, we can extend the result in [8] where the author considered (1.1) with ; and we also improve the result of [9] in the presence of a nonlinear source term. We followed the technique skill introduced in [9] with the concept of a stable set in to derive the optimal decay rate of . The content of this paper is organized as follows. In Section 2, we give some lemmas which will be used later. In Section 3, we derive the global solution and its decay properties with .
2 Preliminary results
In this section, we shall give some lemmas which will be used throughout this work. We denote by the norm over Ω.
Lemma 2.1 (The Sobolev-Poincaré inequality)
If (if), then
holds with some positive constant.
Let be a nonincreasing and nonnegative function on such that
with certain constantsand. Then, the functionsatisfies
for, where we putandif.
Now, we state the local existence for problem (1.1)-(1.3) which can be established by the arguments of [8].
Theorem 2.3 Suppose that, then there exists a unique solution u of problem (1.1)-(1.3) satisfying
Moreover, at least one of the following statements holds true:
-
(i)
,
-
(ii)
, as .
3 Decay properties
In this section, we shall show the decay properties of solutions u to problem (1.1)-(1.3). For this purpose, we define


and the energy function
for , . Then, multiplying (1.1) by and integrating it over Ω, we see that
Lemma 3.1 Let. Suppose that p and γ satisfy
If and
then, for.
Proof Since , then there exists such that
which gives
Thus, from (3.3) and being nonincreasing by (3.4), we have that
And so, exploiting Lemma 2.1, (3.8) and (3.6), we obtain
Therefore,
By repeating this procedure and using the fact that
we can take . □
Lemma 3.2 Let u satisfy the assumptions of Lemma 3.1. Then there existssuch that
with.
Proof From (3.9), we get
Let , then we have the inequality (3.10). □
Theorem 3.3 Suppose that, , (3.5) and (3.6) hold. Then there exists a unique global solution u of problem (1.1)-(1.3) satisfying
Furthermore, we have the following decay estimates:
where α and β are some positive constants given by (3.15).
Proof First, for , we can obtain the result by following the arguments as in [8], so we omit the proof. Next, we will show the decay estimate. For , integrating (3.4) over , we have
Then there exist and such that
Multiplying (1.1) by u, integrating it over , using integration by parts and Lemma 2.1, we get
Hence, from the definition of by (3.1), using (3.12), (3.13) and (3.8), we obtain
On the other hand, integrating (3.4) over , noting that due to , and using (3.3) and (3.7), we have that
We then use the fact that by (3.10), (3.12) and (3.14) to obtain
where
with
Moreover, from (3.12) and being nonincreasing by (3.4), we note that
Thus, by Young’s inequality, (3.15) becomes
This implies that
Therefore, applying Lemma 2.2, we conclude that
□
Remark (i) Based on the estimate (3.11), we have further the following estimates:
where and are some positive constants.
-
(ii)
If , then
(3.18)
with . Indeed, by (3.11), we see that
A direct computation yields the result.
Next, we will improve the decay rate for given by (3.17).
Proposition 3.4 If, then the solution u of problem (1.1)-(1.3) satisfies
whereandare some positive constants.
Proof Multiplying (1.1) by and integrating it over Ω, we have
We now estimate the right-hand side of (3.20). Employing Hölder’s inequality and Young’s inequality, the first term gives
As for the second term, using Hölder’s inequality, Lemma 2.1, Young’s inequality and (3.8) yields
Combining these estimates and using (3.17), we arrive at
where and . Then, from Lemma 2.1, we have
Therefore, the desired estimate (3.19) is obtained. □
In order to obtain the decay estimates for problem (1.1)-(1.3), we need the function and equality (3.22) as in [9]. Define
Multiplying (1.1) by with and integrating it over Ω, we have the following equality:

Proposition 3.5 Let, , (3.5)-(3.6) hold and. Suppose thatforand


Then it holds that, for,


where constantsandare given by (3.31) and (3.36).
Proof (i) In the case , we observe from (3.21) that
Using (3.22) with yields

Now, we estimate the right-hand side of (3.28). So, thanks to Hölder’s inequality, Lemma 2.1, (3.8) and Young’s inequality, we see that
and
Taking into account these two estimates in (3.28) and using by (3.27), we obtain
If , then there exists such that and
Hence
for . Applying (3.18) with , we derive that
with
Therefore, we see that (3.29)-(3.31) hold true for , which gives the estimate (3.25) for .
-
(ii)
In the case , we note from (3.21) that
(3.32)
From (3.22) with , we have
Similar to those estimates, as in the case for , the right-hand side of (3.33) can be estimated as follows:

and
Combining these estimates, (3.33) becomes
where we have used the fact that and on the last inequality with , and .
If , then there exists such that and
Thus
for . Employing (3.18) with gives
with
Therefore, we see that (3.34)-(3.36) hold true for , which gives the estimate (3.26) for . □
Proposition 3.6 Under the same assumptions as in Proposition 3.5, assume further that the initial data satisfies
Then it holds that
whereis a positive constant.
Proof (i) In the case , we obtain from (3.22) with that

As in deriving the estimates for case (i) of Proposition 3.5, we get the following estimates:
and
Thus, using the above estimates in (3.39), together with the fact that by (3.27) and the estimate (3.25), yield
for .
If , then, using by (3.17), we see that
and
which implies that
with and some positive constants , .
-
(ii)
In the case , it follows from (3.22) with that
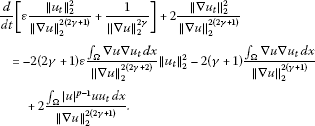 (3.40)
(3.40)
Estimate the right-hand side of (3.40) as in the case (ii) of Proposition 3.5 to obtain
and
Back to (3.40), employing these estimates and using (3.26), we deduce that
for .
If , then, by , we have
and
for with some positive constants , . This implies the desired estimate (3.38) for . □
Now, we are ready to state and prove our main result.
Theorem 3.7 Let, and (3.5)-(3.6) hold. Then the solution u of problem (1.1)-(1.3) satisfies
Moreover, suppose that the initial data satisfiesand
Then
with some positive constants, .
Proof Thanks to the decay estimates (3.11) and (3.17), we obtain (3.41). Setting
then, we see that and for , because of . If , then it holds that
However, from by (3.38), we observe that
which contradicts (3.44). Hence, we have and for all . Therefore, from (3.38), we have
which gives the decay estimate (3.44). □
References
Kirchhoff G: Vorlesungen űber Mechanik. Teubner, Leipzig; 1883.
Hosoys M, Yamada Y: On some nonlinear wave equations II: global existence and energy decay of solutions. J. Fac. Sci., Univ. Tokyo, Sect. 1A, Math. 1991, 38: 239-250.
Nishihara K, Yamada Y: On global solutions of some degenerate quasilinear hyperbolic equations with dissipative terms. Funkc. Ekvacioj 1990, 33: 151-159.
Nakao M: A difference inequality and its application to nonlinear evolution equations. J. Math. Soc. Jpn. 1978, 30: 747-762. 10.2969/jmsj/03040747
Nishihara K: Decay properties of solutions of some quasilinear hyperbolic equations with strong damping. Nonlinear Anal. 1993, 21: 17-21. 10.1016/0362-546X(93)90174-Q
Nishihara K, Ono K: On a nonlinear degenerate integro-differential equation of hyperbolic type with a strong dissipation. Adv. Math. Sci. Appl. 1995, 5(2):457-476.
Ono K: Global existence and decay properties of solutions for some mildly degenerate nonlinear dissipative Kirchhoff strings. Funkc. Ekvacioj 1997, 40(2):255-270.
Ono K: On global existence, asymptotic stability and blowing up of solutions for some degenerate nonlinear wave equations of Kirchhoff type with strong dissipation. Math. Methods Appl. Sci. 1997, 20: 151-177. 10.1002/(SICI)1099-1476(19970125)20:2<151::AID-MMA851>3.0.CO;2-0
Ono K: On decay properties of solutions for degenerate strongly damped wave equations of Kirchhoff type. J. Math. Anal. Appl. 2011, 381(1):229-239. 10.1016/j.jmaa.2011.03.034
Acknowledgements
This work was funded by National Taipei University of Technology under the project 101T458-13.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, ST. On decay properties of solutions for degenerate Kirchhoff equations with strong damping and source terms. Bound Value Probl 2012, 93 (2012). https://doi.org/10.1186/1687-2770-2012-93
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-93