Approximate method for boundary value problems of anti-periodic type for differential equations with ‘maxima’

Abstract

An algorithm for constructing two sequences of successive approximations of a solution of the nonlinear boundary value problem for a nonlinear differential equation with ‘maxima’ is given. The case of a boundary condition of anti-periodic type is investigated. This algorithm is based on the monotone iterative technique. Two sequences of successive approximations are constructed. It is proved both sequences are monotonically convergent. Each term of the constructed sequences is a solution of an initial value problem for a linear differential equation with ‘maxima’ and it is a lower/upper solution of the given problem. A computer realization of the algorithm is suggested and it is illustrated on a particular example.

MSC:34K10, 34K25, 34B15.

1 Introduction

Differential equations with ‘maxima’ are adequate models of real world problems, in which the present state depends significantly on its maximum value on a past time interval (see [1–4], monograph [5]).

Note that usually differential equations with ‘maxima’ are not possible to be solved in an explicit form and that requires the application of approximate methods. In the current paper, the monotone iterative technique [6, 7], based on the method of lower and upper solutions, is theoretically proved to a boundary value problem for a nonlinear differential equation with ‘maxima’. The case when the nonlinear boundary function is a nondecreasing one with respect to its second argument is studied. This type of the boundary function covers the case of an anti-periodic boundary condition. An improved algorithm of monotone-iterative techniques is suggested. The main advantage of this scheme is connected with the construction of the initial conditions.

2 Preliminary notes and definitions

Let $0<T<\mathrm{\infty }$ be a given fixed point and h be a positive constant. Consider the set

$$P(h,T)=\{u:[-h,T]\to \mathbb{R}:u\in C([-h;0],\mathbb{R}),u\in C^1([0,T],\mathbb{R})\}.$$

Consider the following nonlinear differential equation with ‘maxima’:

$$x^{\prime }(t)=f(t,x(t),\underset{s\in [t-h,t]}{max}x(s))\text{for }t\in [0,T],$$

(1)

with a boundary condition

$$g(x(0),x(T))=0,$$

(2)

and an initial condition

$$x(t)=x(0)\text{for }t\in [-h,0],$$

(3)

where $x\in \mathbb{R}$, $f:[0,T]\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$, $g:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$.

In this paper, we study boundary condition (2) in the case when the function $g(x,y)$ is nondecreasing with respect to its second argument y. So, the anti-periodic boundary value problem is a partial case of boundary condition (2). Note that similar problems are investigated for ordinary differential equations [8], delay differential equations [9] and impulsive differential equations [10], and some approximate methods are suggested. The presence of the maximum of the unknown function requires additionally some new comparison results, existence results as well as a new algorithm for constructing successive approximations to the exact unknown solution.

Let $\alpha ,\beta \in C([-h,T],\mathbb{R})$ be such that $\alpha (t)\le \beta (t)$ on $[-h,T]$. Define the following sets:

Definition 1 The function $g:W(\alpha ,\beta )\to \mathbb{R}$ is said to be from the class $L(\gamma ,\alpha ,\beta )$ if for any $v\in [\alpha (T),\beta (T)]$ and for any $u_1,u_2\in [\alpha (0),\beta (0)]$ such that $u_1\ge u_2$, the inequality $g(u_1,v)-g(u_2,v)\le \gamma (u_1-u_2)$ holds.

Definition 2 The function $g:W(\alpha ,\beta )\to \mathbb{R}$ is said to be quasi-nondecreasing in $W(\alpha ,\beta )$ if for any $x\in [\alpha (0),\beta (0)]$ and for any $y_1,y_2\in [\alpha (T),\beta (T)]$ such that $y_1\le y_2$, the inequality $g(x,y_1)\le g(x,y_2)$ holds.

In connection with the construction of successive approximations, we will introduce a couple of quasi-solutions of boundary value problem (1)-(3).

Definition 3 We will say that the functions $\alpha ,\beta \in P(h,T)$ form a couple of quasi-solutions of boundary value problem (1)-(3), if they satisfy the equations $g(\alpha (0),\beta (T))=g(\beta (0),\alpha (T))=0$, (1) and (3).

Definition 4 We will say that the functions $\alpha ,\beta \in P(h,T)$ form a couple of quasi-lower and quasi-upper solutions of boundary value problem (1)-(3), if

(4)

and

(5)

In the proof of our main results, we will use the following lemma.

Lemma 1 (Comparison result)

Let the following conditions be fulfilled:

• 1. The functions $M,L\in C([0,T],{\mathbb{R}}_{+})$ satisfy the inequality

  $$\underset{t\in [0,T]}{max}[M(t)+L(t)]\le T^{-1}.$$

  (6)

• 2. The function $u\in P(h,T)$ satisfies the inequalities

  

  (7)
  

  (8)

Then $u(t)\le 0$ for $t\in [-h,T]$.

Proof Assume the statement of Lemma 1 is not true. Consider the following two cases.

Case 1: Let $u(0)<0$. According to the assumption, it follows that there exists $\eta \in (0,T)$ such that $u(t)<0$ for $t\in [-h,\eta )$, $u(\eta )=0$ and $u^{\prime }(\eta -0)>0$.

Denote ${min}_{t\in [-h,\eta ]}u(t)=-\lambda <0$, where λ is a positive constant. Let the point $\xi \in [0,\eta )$ be such that $u(\xi )=-\lambda$.

According to the mean value theorem, it follows that there exists $\zeta \in (\xi ,\eta )$ such that

$$u(\eta )-u(\xi )=u^{\prime }(\zeta )(\eta -\xi ).$$

(9)

From inequalities $-\lambda \le {min}_{s\in [\zeta -h,\zeta ]}u(s)$, $-\lambda \le u(\zeta )$ and (7), we obtain

$$\begin{array}{rl}\lambda & =u(\eta )-u(\xi )=u^{\prime }(\zeta )(\eta -\xi )\\ \le [-M(\zeta )u(\zeta )-L(\zeta )\underset{s\in [\zeta -h,\zeta ]}{min}u(s)](\eta -\xi )\\ \le [M(\zeta )+L(\zeta )]\lambda (\eta -\xi )\\ <(M(\zeta )+L(\zeta ))\lambda T.\end{array}$$

(10)

Inequality (10) contradicts (6).

Case 2: Let $u(0)=0$. Define a function $\tilde{u}\in P(h,T)$ by the equality $\tilde{u}(t)=u(t)-\delta$, where $\delta >0$ is a small enough constant.

Therefore, $\tilde{u}(0)<0$ and $\tilde{u}(t)$ satisfies inequality (7). From case 1 it follows $\tilde{u}(t)\le 0$ for $t\in [-h,T]$. Take a limit as $\delta \to 0$ and obtain $u(t)\le 0$ for $t\in [-h,T]$. □

In our further investigations, we will use the following result for differential equations with ‘maxima’ which is a partial case of Theorem 3.1.1 [5].

Lemma 2 (Existence and uniqueness)

Let the following conditions be fulfilled:

• 1. The function $Q\in C([0,T],\mathbb{R})$.

• 2. The functions $M,L\in C([0,T],\mathbb{R})$ and satisfy inequality (6).

Then the initial value problem for a linear differential equation with ‘maxima’

has a unique solution $u(t)\in P(h,T)$.

3 Monotone-iterative method

We will give an algorithm for obtaining an approximate solution of the boundary value problem for a nonlinear differential equation with ‘maxima’ (1)-(3).

Theorem 1 Let the following conditions be fulfilled:

• 1. The functions ${\alpha }_0,{\beta }_0\in P(h,T)$ form a couple of quasi-lower and quasi-upper solutions of (1)-(3) such that ${\alpha }_0(t)\le {\beta }_0(t)$ for $t\in [-h,T]$.

• 2. The function $g\in C(W({\alpha }_0,{\beta }_0),\mathbb{R})$ is quasi-nondecreasing in $W({\alpha }_0,{\beta }_0)$ and $g\in L(\gamma ,{\alpha }_0,{\beta }_0)$.

• 3. The function $f\in C(\mathrm{\Omega }({\alpha }_0,{\beta }_0),\mathbb{R})$ and for $(t,x_1,y_1),(t,x_2,y_2)\in \mathrm{\Omega }({\alpha }_0,{\beta }_0)$ such that $x_1\le x_2$, $y_1\le y_2$ the inequality

  $$f(t,x_1,y_1)-f(t,x_2,y_2)\le -M(t)[x_1-x_2]-L(t)[y_1-y_2]$$

holds, where the functions $M,L\in C([0,T],{\mathbb{R}}_{+})$ satisfy inequality (6).

Then there exist two sequences ${\{{\alpha }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\beta }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ such that

• (a) The functions ${\alpha }_n,{\beta }_n\in P(h,T)$ ($n=1,2,\dots$) and $({\alpha }_n,{\beta }_n)$ is a couple of quasi-lower and quasi-upper solutions of boundary value problem (1)-(3).

• (b) The sequence ${\{{\alpha }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ is nondecreasing.

• (c) The sequence ${\{{\beta }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ is nonincreasing.

• (d) For $t\in [-h,T]$ the inequalities

  

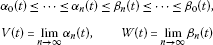  (11)

hold.

• (e) Both sequences are uniformly convergent on $[-h,T]$, and $(V,W)$ is a couple of quasi-solutions of boundary value problem (1)-(3) in $S({\alpha }_0,{\beta }_0)$.

• (f) If additionally the function $f(t,x,y)$ is Lipschitz in $\mathrm{\Omega }({\alpha }_0,{\beta }_0)$, then there exists a unique solution $u(t)$ of boundary value problem (1)-(3) and ${lim}_{n\to \mathrm{\infty }}{\alpha }_n(t)={lim}_{n\to \mathrm{\infty }}{\beta }_n(t)=V(t)=W(t)=u(t)$ for $t\in [-h,T]$.

Proof We will give an algorithm for construction of successive approximations to the unknown exact solution of nonlinear boundary value problem (1)-(3).

Assume the functions ${\alpha }_j(t)$ and ${\beta }_j(t)$, $j=0,1,\dots ,n$, are constructed. Then consider both initial value problems for the linear differential equations with ‘maxima’

(12)

(13)

and

(14)

(15)

where

$$Q_{n+1}(t)=f(t,{\alpha }_n(t),\underset{s\in [t-h,t]}{max}{\alpha }_n(s))+M(t){\alpha }_n(t)+L(t)\underset{s\in [t-h,t]}{max}{\alpha }_n(s)$$

and

$$P_{n+1}(t)=f(t,{\beta }_n(t),\underset{s\in [t-h,t]}{max}{\beta }_n(s))+M(t){\beta }_n(t)+L(t)\underset{s\in [t-h,t]}{max}{\beta }_n(s).$$

According to Lemma 2, initial value problems (12), (13) and (14), (15) have unique solutions ${\alpha }_{n+1},{\beta }_{n+1}\in P(h,T)$.

So, step by step we can construct two sequences of functions ${\{{\alpha }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\beta }_n(t)\}}_{n=0}^{\mathrm{\infty }}$.

Now, we will prove by induction that for $j=0,1,2,\dots$ ,

(H1) ${\alpha }_{j+1}(t)\ge {\alpha }_j(t)$ and ${\beta }_{j+1}(t)\le {\beta }_j(t)$ for $t\in [-h,T]$;

(H2) ${\alpha }_{j+1}(t)\le {\beta }_{j+1}(t)$ for $t\in [-h,T]$;

(H3) $({\alpha }_{j+1},{\beta }_{j+1})$ is a couple of quasi-lower and quasi-upper solutions of boundary value problem (1)-(3).

Assume the claims (H1)-(H3) are satisfied for $j=0,1,\dots ,n-1$.

We will prove (H1) for $j=n$.

Define the function $p_1\in P(h,T)$ by the equality $p_1(t)={\alpha }_n(t)-{\alpha }_{n+1}(t)$.

Let $t\in [-h,0]$. Then according to condition 2 of Theorem 1, the inductive assumption and the definition of the functions ${\alpha }_n(t)$, ${\alpha }_{n+1}(t)$, we have

$$\begin{array}{rcl}{p}_1(t)& =& {\alpha }_{n-1}(0)-{\alpha }_n(0)\\ +\frac{1}{\gamma }[g({\alpha }_n(0),{\beta }_n(T))-g({\alpha }_{n-1}(0),{\beta }_{n-1}(T))]\\ =& {\alpha }_{n-1}(0)-{\alpha }_n(0)\\ +\frac{1}{\gamma }[g({\alpha }_n(0),{\beta }_n(T))-g({\alpha }_{n-1}(0),{\beta }_n(T))]\\ +\frac{1}{\gamma }[g({\alpha }_{n-1}(0),{\beta }_n(T))-g({\alpha }_{n-1}(0),{\beta }_{n-1}(T))]\\ \le & 0.\end{array}$$

(16)

Let $t\in [0,T]$. From (H1) for $j=n-1$, condition 3 of Theorem 1, the definition of the functions ${\alpha }_n(t)$, ${\alpha }_{n+1}(t)$ and (12), we get

$$\begin{array}{rcl}{p}_1^{\prime }(t)& \le & -M(t)[{\alpha }_n(t)-{\alpha }_{n+1}(t)]\\ -L(t)[\underset{s\in [t-h,t]}{max}{\alpha }_n(s)-\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s)].\end{array}$$

(17)

Note that for any $t\in [0,T]$ the following inequality holds:

$$\underset{s\in [t-h,t]}{max}{\alpha }_n(s)-\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s)\ge \underset{s\in [t-h,t]}{min}[{\alpha }_n(s)-{\alpha }_{n+1}(s)].$$

(18)

From inequalities (17) and (18) it follows

$$p_1^{\prime }(t)\le -M(t)p_1(t)-L(t)\underset{s\in [t-h,t]}{min}{p}_1(s).$$

According to Lemma 1, we get $p_1(t)\le 0$ for $t\in [-h,T]$. Thus, ${\alpha }_n(t)\le {\alpha }_{n+1}(t)$ for $t\in [-h,T]$.

Define the function $p_2\in P(h,T)$ by the equality $p_2(t)={\beta }_{n+1}(t)-{\beta }_n(t)$. Then for $t\in [-h,0]$ we have

$$\begin{array}{rcl}{p}_2(t)& =& {\beta }_n(0)-{\beta }_{n-1}(0)\\ +\frac{1}{\gamma }[g({\beta }_{n-1}(0),{\alpha }_{n-1}(T))-g({\beta }_n(0),{\alpha }_n(T))]\\ =& {\beta }_n(0)-{\beta }_{n-1}(0)\\ +\frac{1}{\gamma }[g({\beta }_{n-1}(0),{\alpha }_{n-1}(T))-g({\beta }_n(0),{\alpha }_{n-1}(T))]\\ +\frac{1}{\gamma }[g({\beta }_n(0),{\alpha }_{n-1}(T))-g({\beta }_n(0),{\alpha }_n(T))]\\ \le & 0.\end{array}$$

(19)

From equation (14), the inductive assumption, the definition of the functions ${\beta }_n(t)$, ${\beta }_{n+1}(t)$ and condition 3 of Theorem 1, it follows the validity of the inequality

$$p_2^{\prime }(t)\le -M(t)p_2(t)-L(t)\underset{s\in [t-h,t]}{min}{p}_2(s).$$

According to Lemma 1, we get $p_2(t)\le 0$ for $t\in [-h,T]$, i.e., the claim (H1) is true for $j=n$.

Define the function $p_3\in P(h,T)$ by the equality $p_3(t)={\alpha }_{n+1}(t)-{\beta }_{n+1}(t)$.

Let $t\in [-h,0]$. From condition 2 of Theorem 1, the inductive assumption and the definition of the functions ${\alpha }_{n+1}(t)$, ${\beta }_{n+1}(t)$, we obtain

$$\begin{array}{rcl}{p}_3(t)& =& {\alpha }_n(0)-{\beta }_n(0)+\frac{1}{\gamma }[g({\beta }_n(0),{\alpha }_n(T))-g({\alpha }_n(0),{\alpha }_n(T))]\\ +\frac{1}{\gamma }[g({\alpha }_n(0),{\alpha }_n(T))-g({\alpha }_n(0),{\beta }_n(T))]\\ \le & 0.\end{array}$$

Let $t\in [0,T]$. According to the choice of the functions ${\alpha }_{n+1}(t)$, ${\beta }_{n+1}(t)$, condition 3 of Theorem 1 and inequality ${max}_{s\in [t-h,t]}{\alpha }_{n+1}(s)-{max}_{s\in [t-h,t]}{\beta }_{n+1}(s)\ge {min}_{s\in [t-h,t]}[{\alpha }_{n+1}(s)-{\beta }_{n+1}(s)]$, we get

$$p_3^{\prime }(t)\le -M(t)p_3(t)-L(t)\underset{s\in [t-h,t]}{min}{p}_3(s).$$

According to Lemma 1, it follows $p_3(t)\le 0$ for $t\in [-h,T]$. Therefore, the claim (H2) is satisfied for $j=n$.

Now, we will prove the claim (H3) for $j=n$.

Let $t\in [-h,0]$. Then from (13) we get

$${\alpha }_{n+1}(t)={\alpha }_n(0)-\frac{1}{\gamma }g({\alpha }_n(0),{\beta }_n(T))={\alpha }_{n+1}(0).$$

(20)

From (H1) for $j=n$, condition 2 of Theorem 1 and the choice of the function ${\alpha }_{n+1}(t)$, we obtain

(21)

Let $t\in [0,T]$. From condition 3 of Theorem 1, inequalities (18) and (H1), we get

$$\begin{array}{rcl}{\alpha }_{n+1}^{\prime }(t)& =& -M(t)[{\alpha }_{n+1}(t)-{\alpha }_n(t)]\\ -L(t)[\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s)-\underset{s\in [t-h,t]}{max}{\alpha }_n(s)]\\ +f(t,{\alpha }_{n+1}(t),\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s))\\ +[f(t,{\alpha }_n(t),\underset{s\in [t-h,t]}{max}{\alpha }_n(s))\\ -f(t,{\alpha }_{n+1}(t),\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s))]\\ \le & f(t,{\alpha }_{n+1}(t),\underset{s\in [t-h,t]}{max}{\alpha }_{n+1}(s)).\end{array}$$

(22)

Similarly, we prove the function ${\beta }_{n+1}(t)$ satisfies inequalities (5). Therefore, the claim (H3) is true for $j=n$. Furthermore, the functions ${\alpha }_{n+1}(t),{\beta }_{n+1}(t)\in S({\alpha }_n,{\beta }_n)$.

For any fixed $t\in [-h,T]$, the sequences ${\{{\alpha }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\beta }_n(t)\}}_{n=0}^{\mathrm{\infty }}$ are nondecreasing and nonincreasing, respectively, and they are bounded by ${\alpha }_0(t)$ and ${\beta }_0(t)$.

Therefore, both sequences converge pointwisely and monotonically. Let ${lim}_{n\to \mathrm{\infty }}{\alpha }_n(t)=V(t)$ and ${lim}_{n\to \mathrm{\infty }}{\beta }_n(t)=W(t)$ for $t\in [-h,T]$. According to Dini’s theorem, both sequences converge uniformly and the functions $V(t)$, $W(t)$ are continuous. Additionally, the claims (H1), (H2) prove $V,W\in S({\alpha }_0,{\beta }_0)$.

Now, we will prove that for any $t\in [0,T]$ the following equality holds:

$$\underset{n\to \mathrm{\infty }}{lim}[\underset{\xi \in [t-h,t]}{max}{\alpha }_n(\xi )]=\underset{\xi \in [t-h,t]}{max}[\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n(\xi )].$$

(23)

For any $t\in [0,T]$, we introduce the notation ${max}_{{\xi }_t\in [t-h,t]}{\alpha }_n({\xi }_t)=A_n(t)$. From condition (H1) it follows that for any ${\xi }_t\in [t-h,t]$ the inequalities ${\alpha }_{n-1}({\xi }_t)\le {\alpha }_n({\xi }_t)\le A_n(t)$ hold and thus, $A_{n-1}(t)\le A_n(t)$, $n=1,2,\dots$ , i.e., the sequence ${\{A_n(t)\}}_{n=0}^{\mathrm{\infty }}$ is monotone nondecreasing and bounded from above by ${\beta }_0(t)$ for any $t\in [-h,T]$. Therefore, there exists the limit $A(t)={lim}_{n\to \mathrm{\infty }}{A}_n(t)$.

From the monotonicity of the sequence of the quasi-lower solutions ${\alpha }_n(t)$, we get that for ${\xi }_t\in [t-h,t]$ the inequality ${\alpha }_n({\xi }_t)\le V({\xi }_t)$ holds. Let ${\eta }_t\in [t-h,t]$ be such that ${max}_{{\xi }_t\in [t-h,t]}V({\xi }_t)=V({\eta }_t)$.

Assume $V({\eta }_t)<A({\eta }_t)$. Then there exists a natural number N such that the inequalities $V({\eta }_t)<A_N({\eta }_t)\le A({\eta }_t)$ hold. Therefore, there exists ${\xi }_t\in [{\eta }_t-h,{\eta }_t]$ such that ${\alpha }_N({\xi }_t)={max}_{{\xi }_t\in [{\eta }_t-h,{\eta }_t]}{\alpha }_N({\xi }_t)=A_N({\eta }_t)$ or $V({\eta }_t)<{\alpha }_N({\xi }_t)\le V({\xi }_t)$. The obtained contradiction proves the assumption is not valid.

Assume $V({\eta }_t)>A({\eta }_t)$. According to the definition of the function $V(t)$, it follows that for the fixed number ${\eta }_t$, we have ${lim}_{n\to \mathrm{\infty }}{\alpha }_n({\eta }_t)=V({\eta }_t)$. Then there exists a natural number N such that $A({\eta }_t)<{\alpha }_N({\eta }_t)\le V({\eta }_t)$ and ${max}_{{\eta }_t\in [t-h,t]}{\alpha }_N({\eta }_t)=A_N({\eta }_t)$. Therefore, ${\alpha }_N({\eta }_t)\le {max}_{{\eta }_t\in [t-h,t]}{\alpha }_N({\eta }_t)\le A({\eta }_t)$. The obtained contradiction proves the assumption is not valid.

Therefore, the required equality (23) is fulfilled.

In a similar way, we can prove that for any $t\in [0,T]$ the equality

$$\underset{n\to \mathrm{\infty }}{lim}[\underset{\xi \in [t-h,t]}{max}{\beta }_n(\xi )]=\underset{\xi \in [t-h,t]}{max}[\underset{n\to \mathrm{\infty }}{lim}{\beta }_n(\xi )]$$

(24)

holds.

Take a limit as $n\to \mathrm{\infty }$ in (13) and get

$$V(t)=V(0)-\frac{1}{\gamma }g(V(0),W(T))\text{for }t\in [-h,0].$$

(25)

From (25) for $t=0$, we get $g(V(0),W(T))=0$.

Taking a limit in the integral equation equivalent to (12), we obtain the function $V(t)$ satisfies equation (1) for $t\in [0,T]$.

In a similar way, we can prove that $W(t)$ satisfies equation (1) for $t\in [0,T]$ and $g(W(0),V(T))=0$. Therefore, the couple $(V,W)$ is a couple of quasi-solutions of (1)-(3) in $S({\alpha }_0,{\beta }_0)$ such that $V(t)\le W(t)$ for $t\in [-h,T]$.

Let the function $f(t,x,y)$ be Lipschitz. Then if (1) has a solution $u(t)$, it is unique (see [11]). In this case, $V(t)\equiv W(t)$ and for $t\in [-h,T]$,

$$\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n(t)=\underset{n\to \mathrm{\infty }}{lim}{\beta }_n(t)=V(t)=W(t)=u(t).$$

 □

4 Applications

We will apply the given above algorithm for approximate solving of a nonlinear boundary value problem.

Example

Consider the following nonlinear boundary value problem for a nonlinear differential equation with ‘maxima’:

(26)

(27)

Boundary value problem (26), (27) is of type (1)-(3), where $h=0.1$, $T=0.3$, $f(t,x,y)=\frac{1}{2-x}-2y-\frac{1}{2}$ and $g(x,y)=3x+x^2+e^y-1$.

Let ${\alpha }_0(t)\equiv -1$ and ${\beta }_0(t)\equiv 1$. The couple $({\alpha }_0(t),{\beta }_0(t))$ is a couple of quasi-lower and quasi-upper solutions of boundary value problem (26), (27).

Let $(t,x_1,x_2),(t,y_1,y_2)\in \{(t,u,v)\in [0,0.3]\times [-1,1]\times [-1,1]\}$ and $x_i\le y_i$, $i=1,2$. Therefore,

$$f(t,x_1,x_2)-f(t,y_1,y_2)=\frac{x_1-y_1}{(2-x_1)(2-y_1)}-2[x_2-y_2]\le -M(t)(x_1-y_1)-L(t)(x_2-y_2),$$

where $M(t)\equiv 1$, $L(t)\equiv 2$ for $t\in [0,0.3]$. Thus, condition 3 of Theorem 1 holds.

The function $g(x,y)$ is quasi-nondecreasing with respect to y and $g\in L(\gamma ,{\alpha }_0,{\beta }_0)$, $\gamma =5$.

The above given problem has a zero solution. We will apply the procedure given in Theorem 1 to obtain two sequences, which are monotonically convergent to 0.

The function ${\alpha }_n(t)$, $n\ge 1$, is a solution of problem (12), (13), which is reduced to the following linear initial value problem:

$$\begin{array}{r}{\alpha }_n^{\prime }(t)=-{\alpha }_n(t)-2\underset{s\in [t-0.1,t]}{max}{\alpha }_n(s)-\frac{1}{2}\\ \phantom{{\alpha }_n^{\prime }(t)=}+\frac{1}{2-{\alpha }_{n-1}(t)}+{\alpha }_{n-1}(t),t\in [0,0.3],\\ {\alpha }_n(t)=0.4{\alpha }_{n-1}(0)-0.2{({\alpha }_{n-1}(0))}^2\\ \phantom{{\alpha }_n(t)=}-0.2e^{{\beta }_{n-1}(0.3)}+0.2,t\in [-0.1,0].\end{array}$$

(28)

The function ${\beta }_n(t)$, $n\ge 1$, is a solution of problem (14), (15), which is reduced to the following linear initial value problem:

$$\begin{array}{r}{\beta }_n^{\prime }(t)=-{\beta }_n(t)-2\underset{s\in [t-0.1,t]}{max}{\beta }_n(s)-\frac{1}{2}\\ \phantom{{\beta }_n^{\prime }(t)=}+\frac{1}{2-{\beta }_{n-1}(t)}+{\beta }_{n-1}(t),t\in [0,0.3],\\ {\beta }_n(t)=0.4{\beta }_{n-1}(0)-0.2{({\beta }_{n-1}(0))}^2\\ \phantom{{\beta }_n(t)=}-0.2e^{{\alpha }_{n-1}(0.3)}+0.2,t\in [-0.1,0].\end{array}$$

(29)

According to Lemma 2, initial value problems (28) and (29) have unique solutions ${\alpha }_n(t)$ and ${\beta }_n(t)$, respectively. Because of the presence of the maximum of the unknown function over a past time interval, there is no explicit formula for the exact solutions of (28) and (29). We use a computer program based on a modified numerical method to solve these problems (see [12]).

Also, by a computer realization of the scheme given in Theorem 1 and applied to problems (28) and (29), we obtain the values in Table 1.

Table 1 Values of the successive approximations ${\mathit{\alpha }}_{\mathit{n}}\mathbf{(}\mathit{t}\mathbf{)}$ and ${\mathit{\beta }}_{\mathit{n}}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{n}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{4}\mathbf{,}\mathbf{5}$

From Table 1 and Figure 1, it is obvious that the sequence $\{{\alpha }_n(t)\}$ is increasing and the sequence $\{{\beta }_n(t)\}$ is decreasing and both monotonically converge to the unique solution 0 of nonlinear boundary value problem (26), (27).

Figure 1

Graphic of the successive approximations ${\mathit{\alpha }}_{\mathit{n}}\mathbf{(}\mathit{t}\mathbf{)}$ and ${\mathit{\beta }}_{\mathit{n}}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{n}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{4}\mathbf{,}\mathbf{5}$ .