- Research
- Open access
- Published:
Existence of positive ground states for some nonlinear Schrödinger systems
Boundary Value Problems volume 2013, Article number: 13 (2013)
Abstract
We prove the existence of positive ground states for the nonlinear Schrödinger system
where a, b are periodic or asymptotically periodic and F satisfies some superlinear conditions in . The proof is based on the method of Nehari manifold and the concentration-compactness principle.
MSC:35J05, 35J50, 35J61.
1 Introduction and statement of the main result
This paper was motivated by the following two-component system of nonlinear Schrödinger equations:
where , , and . The system (1.1) has applications in many physical problems, especially in nonlinear optics (see [1]). To obtain standing wave solutions of (1.1) of the form , with , the system (1.1) turns out to be
Following the work [2] by Lin and Wei about the existence of ground states for the problem (1.2), there are many results on the existence of ground states relevant to five parameters (, , , and β); see [3–9] and the references therein. Later in [10], assuming , Pomponio and Secchi established the existence of radially symmetric ground states for (1.2) with general nonlinearities ( and ).
On the other hand, some authors considered the existence of ground states for non-autonomous similar problems. We recall the results about non-autonomous case for two subcases. For periodic case, in [11] Szulkin and Weth referred that treating as periodic Schrödinger equations, it is possible to deduce that there are ground states for the following system using the method of Nehari manifold:
where G is periodic in x and satisfies some superlinear conditions in . For non-periodic case, we refer to [8, 12–14] for instance. As we can observe, most of the previous results on ground states for the non-periodic system have used the condition that there exists a limit system (or the problem at infinity; for precise statement, refer to [15]). Moreover, the limit system is autonomous. Here we mainly deal with an asymptotically periodic Schrödinger system which has a periodic non-autonomous limit system, roughly speaking. In this paper, we are concerned with the existence of positive ground states for the nonlinear Schrödinger system in ()
where is a real parameter. For simplicity, we denote +∞ by ∞
Moreover, in what follows, the notation inf (sup) is understood as the essential infimum (supremum). In the sequel, let and with , we always assume that
(V1) , ,
(F1) for some and ,
(F2) as ,
(F3) , , is strictly increasing,
(F4) as ,
(F5) , , , , ,
(F6) , .
(F1)-(F4) are similar to the conditions of the nonlinearities for the periodic system (1.3) as considered in [11]. We divide the study of (NLS) into two cases as follows.
First, we consider the periodic case
(V2) , , , .
We have the following result.
Theorem 1.1 Let (V1), (V2) and (F1)-(F6) hold. Then the system (NLS) has a positive ground state.
Remark 1.1 It is observed that the system (NLS) with periodic a and b is a particular case of the problem (1.3) with
and G is periodic in x. The problem (1.3) is mentioned in [11] when G is periodic in x. However, in [11] the conditions on the function G are not made explicit.
Next, we consider the asymptotically periodic case. We assume that there are functions satisfying (V1) and (V2) and a, b satisfies that
(V3) , ,
(V4) , .
We have the following result.
Theorem 1.2 Assume that and satisfy (V2). Let (V1), (V3), (V4) and (F1)-(F6) hold. Then the system (NLS) has a positive ground state.
Remark 1.2 Conditions (V1) and (V4) imply that and satisfy (V1).
In addition, we consider the following conditions:
(V5) , ,
(F7) , , .
We have the following result.
Theorem 1.3 Suppose that and satisfy (V1) and (V2). Let (V1), (V3), (V5) and (F1)-(F7) hold. Then the system (NLS) has a positive ground state.
We will prove Theorems 1.1, 1.2 and 1.3 using the method of Nehari manifold. We first reduce the problem of seeking for ground states of (NLS) into that of looking for minimizers of the functional constrained on the Nehari manifold. Then we apply the concentration-compactness principle to solve the minimization problem. Since the Nehari manifold for (NLS) may not be smooth, in the same way as [11], we will make use of the differential structure of a unit sphere in to find a sequence (c is the infimum of the functional constrained on the Nehari manifold). When (NLS) is periodic, we will use the invariance of the functional under translation to recover the compactness of the sequence. When the system (NLS) is asymptotically periodic, the difficulty is to recover the compactness for the sequence. By comparing c with the infimum of the functional of the related periodic limit system constrained on the corresponding Nehari manifold, we will restore the compactness.
The paper is organized as follows. In Section 2 we give some preliminaries. In Section 3 we introduce the variational setting. In Section 4 we consider the periodic case and prove Theorem 1.1. Section 5 is devoted to studying the asymptotically periodic case and showing Theorems 1.2 and 1.3.
2 Notation and preliminaries
We use the following notation:
-
For simplicity, we denote and , where is measurable.
-
X denotes the Sobolev space (), with the standard scalar product and the norm . with the norm . When there is no possible misunderstanding, the subscripts could be omitted.
-
The usual norm in () will be denoted by .
-
.
-
For any and , denotes the ball of radius ϱ centered at z.
Note that and . Then by conditions (F1) and (F2), the functional
is of class and its critical points are solutions of (NLS). Moreover, by (V1) we have
with .
A solution of (NLS) is called a ground state if
A ground state such that , (, ) is called a positive (non-negative) ground state. Below we give some lemmas useful for studying our problem.
Lemma 2.1 (F1) and (F2) imply that for all , there exists such that
(F2) and (F3) yield that
Moreover, (F3) implies the function is increasing in for all .
Proof The inequalities (2.2) and (2.3) are easily inferred from the corresponding assumptions. We just prove the last conclusion. Indeed, let . Then by (F3) we obtain
□
Lemma 2.2 Let (F1) and (F2) hold. Then is weakly sequentially continuous. Namely, if in H, then in H.
Proof Suppose in H. After passing to a subsequence, we assume in . By (F1), we get
Then for all , we have
So, one easily has that
Now, we claim that is bounded in H. Indeed, for , using (2.2) and the Hölder inequality, we obtain that
Similarly, we get . Then we easily have
Hence, is bounded in H. Combining with the fact that is dense in H, we easily deduce that (2.4) holds for any . Therefore, in H. □
3 Variational setting
This section is devoted to describing the variational framework for the study of ground states for (NLS).
It is easy to see that Φ is bounded neither from above nor from below. So, it is convenient to consider Φ on the Nehari manifold that contains all nontrivial critical points of Φ and on which Φ turns out to be bounded from below. The Nehari manifold M corresponding to Φ is defined by
where
Below we investigate the main properties of Φ on M.
Lemma 3.1 Let (F2) and (F3) hold. Then Φ is bounded from below on M by 0.
Proof
Note that
By (2.3) we have . □
Define the least energy of (NLS) on M by , then . Next, we prove M is a manifold. First, we give the following two lemmas, which will be important when proving M is a manifold.
Lemma 3.2 Let (V1) and (F2)-(F4) hold. Assume in H and . Then for any with and , we have
Moreover, .
Proof Since in H, we assume that in , and a.e. on for a subsequence. By , there exists a positive measure set Ω such that , . Then , . By (F4) we have
Therefore, (2.3) and the Fatou lemma yield that
Using (2.1) we have
since is bounded in H. □
Lemma 3.3 Let (V1) and (F1)-(F4) hold. Then
-
(i)
for each , there exists such that if , then for and for ;
-
(ii)
there exists such that for all ;
-
(iii)
for each compact subset , there exists a constant such that for all .
Proof
-
(i)
Note that
Using (F2), we infer that when t is small enough, . By Lemma 3.2 and (2.3), we have
Then when t is large enough, . Then has maximum points in . Moreover, from (F3) one easily deduces that the critical point of is unique in , and then it is the maximum point. We denote it by . Then for and for .
-
(ii)
If , then
By (2.1) and (2.2), we get
where is arbitrary. Then
So, there exists such that
Using (i), for , there exists such that . Then . Then (3.2) yields the conclusion (ii).
-
(iii)
We argue by contradiction. Suppose that there exist a compact set W and a sequence such that and . Since W is compact, there exists such that in H. Then Lemma 3.2 implies that . Contrary to Lemma 3.1 since . This ends the proof. □
Remark 3.1 Lemma 3.3(i) implies that for each , there exists a unique such that
As a consequence of Lemma 3.3(i), we can define the mapping by . By Lemma 3.3, [[11], Proposition 3.1(b)] yields the following result.
Lemma 3.4 If (V1) and (F1)-(F4) are satisfied, then m is a homeomorphism between S and M, and M is a manifold.
If M is a manifold, we can make use of the differential structure of M to reduce the problem of finding a ground state for (NLS) into that of looking for a minimizer of and solve the minimizing problem. However, since , M may not be a manifold. Noting that M and S are homeomorphic, we will take advantage of the differential structure of S to seek for ground states for (NLS) as [11]. Therefore, as in [11], we introduce the functional defined by , and we have the following conclusion.
Proposition 3.1 Let (V1) and (F1)-(F4) hold. Then the following results hold:
-
(i)
If is a PS sequence for Ψ, then is a PS sequence for Φ.
-
(ii)
is a critical point of Ψ if and only if is a nontrivial critical point of Φ. Moreover, .
-
(iii)
A minimizer of is a solution of (NLS).
Proof As in the proof of [[11], Corollary 3.3], we can show (i) and (ii). Now, we prove the conclusion (iii). Indeed, let such that . Then , where . By the conclusion (ii), we have . So, . Using the conclusion (ii) again, we deduce that . □
From the definition of a ground state, we translate the problem of looking for a ground state for (NLS) into that of seeking for a solution for (NLS) which is a minimizer of . By Proposition 3.1(iii), in order to look for a ground state for (NLS), we just need to seek for a minimizer of .
4 The periodic case
In this section, we consider the periodic case and prove Theorem 1.1. In [11], Szulkin and Weth considered the existence of ground states for periodic single Schrödinger equations. Treating as in [11], we find ground states for a periodic case for the system (NLS). In addition, under conditions (F5) and (F6), we deduce that there are positive ground states.
From the statement in Section 3, it suffices to solve the minimizing problem. By conclusions (i) and (ii) of Proposition 3.1, we first make use of the minimizing sequence of Ψ to obtain a sequence of Φ. Then we use the invariant of the functional under translation of the form , to recover the compactness for the sequence.
Proof of Theorem 1.1 Let be a minimizing sequence of Ψ. By the Ekeland variational principle [[16], Theorem 8.5], we may assume that . Using Proposition 3.1(i), we have that , where . Proposition 3.1(ii) implies that .
We claim that is bounded in H. Otherwise, suppose up to a subsequence. Set . Then we assume in H, in and a.e. on after passing to a subsequence. Moreover, the Sobolev embedding theorem implies that is bounded in , namely, is bounded. Taking a subsequence, we suppose .
-
(i)
If , then for any , there exists such that , for . Combining with (2.2), for and , we have
Then . Hence, by (2.1) we get
a contradiction for .
-
(ii)
If , then we can assume that
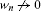 in . From the Lions compactness lemma [[16], Lemma 1.21], it follows that there exist and such that (4.1)
in . From the Lions compactness lemma [[16], Lemma 1.21], it follows that there exist and such that (4.1)
Since Φ and M are invariant by translation of the form , , translating if necessary, we may assume is bounded. Since in , then (4.1) implies . Then from Lemma 3.2, we deduce that . This is impossible since .
Hence, is bounded in H. Suppose that in H, in and a.e. on for a subsequence. Since , Lemma 2.2 yields .
We will show that . Similarly, suppose . If , then as before, combining with (2.2), we obtain that . Hence, by (2.1) we have
Then in H. This is impossible since and (3.2) holds. Therefore, . So, we can assume  in . Then the Lions compactness lemma implies that there exist , such that
in . Then the Lions compactness lemma implies that there exist , such that
As before, translating if necessary, we may assume is bounded. Since (4.2) and in , we get . Note that . So, . Then by (3.1) we get
where (4.3) follows from the Fatou lemma and (2.3). Then . According to , we have . Thus, . Consequently, is a ground state of (NLS).
It remains to look for a positive ground state for (NLS). First, we can assume that is non-negative. In fact, note that and for all . Then . Let be such that . By (F6) we easily have that . Moreover, since . Then . So, is also a minimizer of Φ on M. Then is also a ground state of (NLS). Thus we can assume that is a non-negative ground state for (NLS). Now, we claim that , . Indeed, if , then from (F5) and , the first equation of (NLS) yields that . Then . This is impossible. So, . Similarly, . By (F5), applying the maximum principle to each equation of (NLS), we infer that , . The proof is complete. □
5 The asymptotically periodic case
In this section, we will consider the asymptotically periodic case and prove Theorems 1.2 and 1.3. As in the proof of Theorem 1.1, we first take advantage of the minimizing sequence of Ψ to find a sequence of Φ. In what follows, the important thing is to recover the compactness for the sequence. For this purpose, we need to estimate the functional levels of the problem (NLS) and those of a related periodic problem of (NLS) (roughly speaking, the limit system of (NLS) by (V3))

Hence, first we introduce some definitions and look for solutions for the problem (NLS) p . The functional of (NLS) p is defined by
The Nehari manifold of (NLS) p is
and is the least energy of (NLS) p on . Note that
As for c, we have .
Lemma 5.1 Suppose that , satisfy (V1) and (V2). Let (F1)-(F6) hold. Then the problem (NLS) p has a positive ground state such that .
Proof As a corollary of Theorem 1.1, we infer that the problem (NLS) p has a positive ground state. Moreover, from the argument of Theorem 1.1, we find that the ground state of the problem (NLS) p we obtained is a minimizer of on . □
The existence of a positive ground state for the problem (NLS) p implies that (NLS) has a positive ground state when and . So, it remains to consider
Next, we prove that under some conditions.
Lemma 5.2 Suppose that , satisfy (V2). Let (V1), (V4), (5.2) and (F1)-(F6) hold. Then .
Proof Let be a positive ground state of (NLS) p such that . Assume satisfies . By (V4), we get
Then .
Replacing Φ and M by and respectively, (3.3) also holds. Noting that , we infer that
Therefore,
If , we are done. Otherwise, . Then by (5.3) and (5.4), we get and . Then is a ground state for (NLS). Note that is a solution of (NLS) p . From the first equations of (NLS) and (NLS) p , we infer that . Similarly, contrary to (5.2). The proof is now complete. □
Lemma 5.3 Suppose that , satisfy (V1) and (V2). Let (V1), (V5), (5.2) and (F1)-(F7) hold. Then .
Proof Let be a positive ground state of (NLS) p such that . By (V5) and (F7), we find that is also a minimizer of on . Let be such that . Using (V5), we have . Then
Without loss of generality, we assume that
Then . Below we argue analogously with the proof of Lemma 5.2 to infer that . This ends the proof. □
Now, we are ready to prove Theorems 1.2 and 1.3. The proof is partially inspired by [17], where the authors dealt with Schrödinger-Poisson equations.
Proof of Theorem 1.2 As the argument of Theorem 1.1, we infer that there exists a sequence such that and .
We claim that is bounded in H. Otherwise, suppose up to a subsequence. Set . As in the proof of Theorem 1.1, taking a subsequence, we suppose and exclude the case that . So, , then we can assume that  in . From the Lions compactness lemma, it follows that there exist and such that
in . From the Lions compactness lemma, it follows that there exist and such that
Set and . We assume that in H, in and a.e. on up to a subsequence. Then by
we obtain . So, Lemma 3.2 implies that
Then by (2.1), we get
This is a contradiction.
Hence, is bounded in H. Up to a subsequence, we assume that in H, in and a.e. on . By Lemma 2.2, we have . Namely, is a solution of (NLS).
Below we prove that . We argue by contradiction. Suppose that . By (V3), for any , there exists such that
Note that , after passing to a subsequence, we assume in . So, for the above ϵ, there exists such that for , we have
Combining with (5.5), for , we get
Then . Similarly, . Therefore,
Hence,
Let be such that . We claim that for large n and .
First, we prove that
Otherwise, there exist and a subsequence of , still denoted by , such that for all . From (5.6) we have
Moreover, by , we get
Hence,
By and (F3), we obtain
Similar to the proof of Theorem 1.1, if in , then in H. Contrary to (3.2), since , therefore,  in . Suppose
in . Suppose  in . Then from the Lions compactness lemma, it follows that there exist and such that
in . Then from the Lions compactness lemma, it follows that there exist and such that
We denote and by and . Similarly, we assume that in H, in and a.e. on up to a subsequence. By (5.9), we have
So, . From (5.8), (F3) and the Fatou lemma, we obtain
which is impossible. Consequently, (5.7) holds.
Now, we show that for large n. Indeed, on the contrary, passing to a subsequence, we assume that . Using (3.1) and (5.1), we have
where (5.10) follows from the fact that α is increasing in by Lemma 2.1. Then , contrary to Lemma 5.2. Therefore, combining with (5.7), we may assume that
For and , using (2.2) we get
Combining (5.11) with (5.12), one easily has that
Since and is bounded, we get
Hence, . Then using (5.6), we have . Then . However, Lemma 5.2 implies that . This is a contradiction. Note that this contradiction follows from the hypothesis that . So, . Then .
It suffices to show that . By (3.1) we have
where the inequality (5.13) holds by (2.3) and the Fatou lemma. Then . According to , we have . Then is a ground state for (NLS). Below we argue analogously with the proof of Theorem 1.1 to get a positive ground state for (NLS). The proof is complete. □
Proof of Theorem 1.3 By Lemma 5.3, repeating the argument of Theorem 1.2, we show the existence of a ground state for (NLS) and then look for a positive ground state as the argument of Theorem 1.1. □
References
Akhmediev N, Ankiewicz A: Novel soliton states and bifurcation phenomena in nonlinear fiber couplers. Phys. Rev. Lett. 1993, 70: 2395-2398. 10.1103/PhysRevLett.70.2395
Lin TC, Wei J: Ground state of N coupled nonlinear Schrödinger equations in , . Commun. Math. Phys. 2005, 255: 629-653. 10.1007/s00220-005-1313-x
Ambrosetti A, Colorado E: Standing waves of some coupled nonlinear Schrödinger equations. J. Lond. Math. Soc. 2007, 75: 67-82. 10.1112/jlms/jdl020
Ambrosetti A, Colorado E: Bound and ground states of coupled nonlinear Schrödinger equations. C. R. Math. Acad. Sci. Paris 2006, 342: 453-458. 10.1016/j.crma.2006.01.024
Bartsch T, Wang Z-Q: Note on ground states of nonlinear Schrödinger systems. J. Partial Differ. Equ. 2006, 19: 200-207.
Chang J, Liu Z: Ground states of nonlinear Schrödinger systems. Proc. Am. Math. Soc. 2010, 138: 687-693.
Liu Z, Wang Z-Q: Ground states and bound states of a nonlinear Schrödinger system. Adv. Nonlinear Stud. 2010, 10: 175-193.
Maia LA, Montefusco E, Pellacci B: Positive solutions for a weakly coupled nonlinear Schrödinger system. J. Differ. Equ. 2006, 229: 743-767. 10.1016/j.jde.2006.07.002
Sirakov B:Least energy solitary waves for a system of nonlinear Schrödinger equations in . Commun. Math. Phys. 2007, 271: 199-221. 10.1007/s00220-006-0179-x
Pomponio A, Secchi S: A note on coupled nonlinear Schrödinger systems under the effect of general nonlinearities. Commun. Pure Appl. Anal. 2010, 9: 741-750.
Szulkin A, Weth T: The method of Nehari manifold. In Handbook of Nonconvex Analysis and Applications. Edited by: Gao DY, Motreanu D. International Press, Boston; 2010:597-632.
Ambrosetti A, Cerami G, Ruiz D:Solutions of linearly coupled systems of semilinear non-autonomous equations on . J. Funct. Anal. 2008, 254: 2816-2845. 10.1016/j.jfa.2007.11.013
Hajaiej H: Symmetric ground state solutions of m -coupled nonlinear Schrödinger equations. Nonlinear Anal. 2009, 71: 4696-4704. 10.1016/j.na.2009.03.035
Lin TC, Wei J: Symbiotic bright solitary wave solutions of coupled nonlinear Schröndinger equations. Nonlinearity 2006, 19: 2755-2773. 10.1088/0951-7715/19/12/002
Lions P-L: The concentration-compactness principle in the calculus of variations. The locally compact case. I. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 1984, 1: 109-145.
Willem M Progr. Nonlinear Differential Equations Appl. In Minimax Theorems. Birkhäuser, Basel; 1996.
Alves CO, Souto MAS, Soares SHM: Schrödinger-Poisson equations without Ambrosetti-Rabinowitz condition. J. Math. Anal. Appl. 2011, 377: 584-592. 10.1016/j.jmaa.2010.11.031
Acknowledgements
The authors would like to express their sincere gratitude to the referee for helpful and insightful comments. Hui Zhang was supported by the Research and Innovation Project for College Graduates of Jiangsu Province with contract number CXLX12_0069, Junxiang Xu and Fubao Zhang were supported by the National Natural Science Foundation of China with contract number 11071038.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The paper is a joint work of all the authors who contributed equally to the final version of the paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, H., Xu, J. & Zhang, F. Existence of positive ground states for some nonlinear Schrödinger systems. Bound Value Probl 2013, 13 (2013). https://doi.org/10.1186/1687-2770-2013-13
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-13
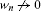 in . From the Lions compactness lemma [[
in . From the Lions compactness lemma [[