- Research
- Open access
- Published:
Reaction-diffusion equations in a noncylindrical thin domain
Boundary Value Problems volume 2013, Article number: 248 (2013)
Abstract
In this paper we are concerned with nonlinear reaction-diffusion equations posed in a time-dependent family of domains which collapses to a lower dimensional set as the parameter ϵ goes to 0.
MSC:35K58, 35B41.
1 Introduction
Evolutionary PDEs on time-varying domains have been the subject of intense research over the past few years; we can cite, for example, [1–6] and the references given therein. Fundamental questions such as existence, regularity, and the asymptotic behavior of solutions are frequent topics of study and, since such problems are intrinsically non-autonomous, they need to be considered in a non-autonomous setting. These problems generate evolution process, and we can indicate the references [7, 8] which include a substantial overview on this topic.
Inspired by the recent works [4, 5], both of them related to reaction-diffusion equations on time-dependent domains, in this paper we are concerned with reaction-diffusion equations in a time-dependent thin domain. To the best of our knowledge, this is an untouched topic in the literature. We are going to prove that the evolution process generated by a family of singularly perturbed reaction-diffusion equations, which is equivalent in the autonomous case to the flow generated by such a family, converges to the evolution process generated by a limiting equation posed in a lower dimensional domain. This is the first step in order to consider the continuity of asymptotic dynamics (attractors), which will be considered in a further work.
One of the pioneering works on (autonomous) nonlinear reaction-diffusion equations on thin domains was [9], where the authors had considered one reaction-diffusion equation posed in the ordinate set under a smooth function satisfying (uniformly in x). They found a limiting equation (), which was defined in a lower dimensional domain, and showed that the flow generated by such an equation behaves continuously (with respect to ϵ in -norms). Our aim in this paper is to prove a similar result for the evolution process generated by equations on time-dependent domains.
In order to set up the problem, let ω be a smooth bounded domain in , , and satisfying
(G1) There exist positive constants and such that
(G2) There exists a constant k such that
where denotes the partial derivative of g with respect to t, denotes the partial derivative of g with respect to , , and is the Euclidian norm in of the vector .
In the following, ϵ denotes a positive parameter which converges to zero. Fixed , we define the time-dependent thin domain
Recalling that , we see that .
For each and , we set the domain
as well as the lateral boundary
where for all .
For positive values of the parameter ϵ, we consider the semilinear reaction-diffusion equation
where denotes the unit outward normal vector field to , denotes the outward normal derivative and is a -function with bounded derivatives up second order.
Besides, since our interest resides in the asymptotic behavior of the solutions and its dependence with respect to ϵ, we will require that solutions of (1.2) are bounded for large values of the time. A natural assumption to obtain this boundedness is expressed in the following dissipative condition:
This implies, for any , the existence of a positive constant such that
We indicate to the interested reader the monograph [[10], Section 4.3].
In the analysis of the limiting behavior of problem (1.2), it will be useful to introduce the domain , independent of ϵ and t, which is obtained from by the change of coordinates
which induces an isomorphism from onto defined by
and with partial derivatives related by
In this new system of coordinates, equation (1.2) can be written as the following non-autonomous equation in the fixed domain Ω:
where η denotes the unit outward normal vector field to ∂ Ω, and
Next, for the reader’s convenience, we argue how to derive equation (1.6) from (1.2). Consider the following variational problem: find such that
for all . After the change of coordinates, we see by (1.5) that (1.7) is equivalent to: find such that
for all .
Stressing the fact that varies in accordance with the time t and the small parameter ϵ collapsing itself to the lower dimensional set , one starts to suspect that tends not to depend on the variable y as . Therefore, we can see immediately from (1.8) that if a limiting regime for problem (1.2) exists, then it should be given by the non-autonomous problem
where ν denotes the unit outward normal vector field to ∂ω.
The paper is organized as follows. In Section 2, we introduce the abstract framework for perturbed problem (1.6) as well as for the limiting one (1.9) and we prove the existence of the associated evolution process. In Section 3 we prove the continuity of such an evolution process uniformly in compact subsets of the real line.
2 Functional setting
In this section we recall the definitions of suitable spaces and operators as well as some of their properties. We start recalling that varies in accordance with a positive parameter ϵ, collapsing itself to the lower dimensional domain ω as ϵ goes to 0. Therefore, in order to preserve the ‘relative capacity’ of a mensurable subset , we rescale the Lebesgue measure of E, , by a factor and we are led to consider the singular measure . This measure has been widely considered in studies involving thin domains, e.g., [9, 11–15], and it allows us to introduce the Lebesgue and the Sobolev spaces.
It will also be convenient to consider the space endowed with the equivalent norm
It is immediate consequence of (G1) that the family of isomorphisms satisfies
for some positive constant c independent of ϵ and t.
For each pair of parameters , we consider the sesquilinear form
Introducing the gradient operator, ,
(2.1) can be written as
As the first remark, notice that under assumption (G1), is a continuous form and there exist positive constants , , independent of ϵ and t, such that
for all and .
Since is densely and compactly embedded in , the sesquilinear form yields a densely defined positive linear operator with compact resolvent, , which is defined by the relation
where .
By the regularity of ∂ω, we have that
is independent of ϵ. Moreover,
Multiplying (1.6) by and integrating by parts, we get
Therefore we can write equation (1.6) as an abstract evolution equation
where is the Nemitskii operator (composition operator) associated to f.
Combining assumptions (G1) and (G2), we also obtain that
for some constant independent of , and . Therefore, thanks to [[16], Theorem 5.4.2], there exists a unique solution of the linear homogeneous problem
This allows us to consider, for each value of the parameter ϵ, each initial time and each initial data , the solution of (2.5). This gives rise to a linear process defined by . We notice that (2.5) is the abstract Cauchy problem associated to equation (1.6) in the case .
Since we are assuming the nonlinearity bounded as well as its derivatives up second order, local existence of the nonlinear counterpart is guaranteed by [[16], Theorem 6.6.1], i.e., writing problem (1.6) as
there exist time and a unique solution of (2.6). Under assumption (1.3) on the nonlinearity f, one can show that actually . Further details can be found in [[10], Section 4.3] and [[17], Theorem 3.2].
Similarly to the linear case, this allows us to consider, for each value of the parameter ϵ, each initial time , and each initial data , the (nonlinear) evolution process in the state space defined by . According to [16],
where is the linear evolution process associated to homogeneous problem (2.5).
For the reader’s convenience, we recall the definition of an evolution process in a Banach space.
Definition 2.1 We say that a family of maps from a Banach space 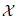 into itself is an evolution process if
into itself is an evolution process if
-
(i)
(identity operator in
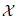 ) for any ,
) for any , -
(ii)
for any ,
-
(iii)
is continuous for all and .
2.1 Limiting consideration
For each , we consider the sesquilinear form
defined by
With this definition, we immediately see that
for all .
Similarly to the previous section, since that is densely and compactly embedded in , gives rise to a densely defined positive linear operator with compact resolvent, , defined by the relation
where , .
By the regularity of ∂ω,
and is independent of t. Moreover,
By (G1)-(G2) there exists a constant (independent of t) such that
for all and .
Therefore, writing equation (1.9) as an abstract evolution equation
we can define an evolution process, , in the state space setting . We notice that
where is the evolution process associated to the linear homogeneous counterpart.
Now we have the elements to state our main result.
Theorem 2.2 Under assumptions (G1), (G2) on the profile , and assuming that the nonlinearity has bounded derivatives up second order and satisfies (1.3), equations (2.6) and (2.10) generate evolution processes and in and , respectively. Moreover, given and such that in , then
uniformly for , , in bounded subsets of , where the extension operator E is defined in (3.2).
3 Convergence results
Due to the nature of this specific kind of singular perturbations, it is natural to introduce the following operators in order to compare functions defined in the different domains Ω and ω.
(Average projector)
(Extension operator)
Notice that the extension operator E maps the family of spaces into .
Lemma 3.1 If is a bounded family in , then is a bounded family in .
Proof For each t fixed, we set . Therefore
In particular, taking as a test function, it follows from (2.2) and Hölder’s inequality that
which proves the result. □
The following lemma describes the behavior of the operators as .
Lemma 3.2 Let be a bounded family in . If weakly in , then
uniformly in t in bounded subsets of ℝ.
Proof If and , then
Besides, for and , we have that
Therefore,
Taking in the last inequality, we derive the result from (2.2) recalling Lemma 3.1. □
Proof of Theorem 2.2 Recalling that the nonlinear term f has bounded derivatives up second order, whenever and does not depend on the variable y, we have that satisfies the following energy estimate:
for some positive constant L (not dependent on ϵ and t) and for all . In particular, taking , we obtain that
It follows from Gronwall’s inequality that
in compact subsets of ℝ.
To conclude, we need to ensure that is uniformly bounded with respect to the parameter ϵ, which is equivalent to ensuring that is uniformly bounded with respect to ϵ. In doing this, we are inspired by the previous argument. In fact, since
we obtain that
which shows that is uniformly bounded. Therefore
for some constant independent of ϵ.
Finally,
for t in compact subsets of ℝ. □
References
Anh CT, Toan ND: Pullback attractors for nonclassical diffusion equations in noncylindrical domains. Int. J. Math. Math. Sci. 2012., 2012: Article ID 875913
Bayada G, Chambat M, Ciuperca I: Comportement asymptotique d’un fluide dans un domaine mince variable en temps. C. R. Math. Acad. Sci. Paris 1998, 326: 265-268. 10.1016/S0764-4442(97)89483-9
Clark HR, Rincon MA, Rodrigues RD: Beam equation with weak-internal damping in domain with moving boundary. Appl. Numer. Math. 2003, 47: 139-157. 10.1016/S0168-9274(03)00066-7
Kloeden PE, Marín-Rubio P, Real J: Pullback attractors for a semilinear heat equation in a non-cylindrical domain. J. Differ. Equ. 2008, 244: 2062-2091. 10.1016/j.jde.2007.10.031
Kloeden PE, Real J, Sun C: Pullback attractors for a semilinear heat equation on time-varying domains. J. Differ. Equ. 2009, 246: 4702-4730. 10.1016/j.jde.2008.11.017
Menezes SB, Limaco J, Medeiros LA: Remarks on null controllability for semilinear heat equation in moving domains. Electron. J. Qual. Theory Differ. Equ. 2003, 16: 1-32.
Carvalho AN, Langa JA, Robinson JC Applied Mathematical Sciences 182. In Attractors for Infinite-Dimensional Non-Autonomous Dynamical Systems. Springer, Berlin; 2012.
Chepyzhov VV, Vishik MI Colloquium Publications 49. In Attractors for Equations of Mathematical Physics. Am. Math. Soc., Providence; 2002.
Hale JK, Raugel G: Reaction-diffusion equation on thin domains. J. Math. Pures Appl. 1992, 71: 33-95.
Hale JK Mathematical Surveys and Monographs 25. In Asymptotic Behavior of Dissipative Systems. Am. Math. Soc., Providence; 1988.
Arrieta JM, Carvalho AN, Pereira MC, Silva RP: Semilinear parabolic problems in thin domains with a highly oscillatory boundary. Nonlinear Anal. 2011, 74: 5111-5132. 10.1016/j.na.2011.05.006
Pereira MC, Silva RP: Error estimates for a Neumann problem in highly oscillating thin domains. Discrete Contin. Dyn. Syst., Ser. A 2013, 33(2):803-817.
Prizzi M, Rybakowski KP: The effect of domain squeezing upon the dynamics of reaction-diffusion equations. J. Differ. Equ. 2001, 173: 271-320. 10.1006/jdeq.2000.3917
Raugel G Lecture Notes in Mathematics 1609. In Dynamics of Partial Differential Equations on Thin Domains. Springer, Berlin; 1995.
Silva RP: A note on resolvent convergence on a thin domain. Bull. Aust. Math. Soc. 2013. 10.1017/S0004972713000555
Tanabe H: Equations of Evolution. Pitman, London; 1979.
Carbone VL, Nascimento MJD, Schiabel-Silva K, Silva RP: Pullback attractors for a singularly nonautonomous plate equation. Electron. J. Differ. Equ. 2011, 77: 1-13.
Acknowledgements
This paper is dedicated in memoriam to José Carlos Arcuri da Silva. RPS is partially supported by FAPESP #2012/06753-8, FUNDUNESP # 0135812 and FUNDUNESP–PROPe #0019/008/13, Brazil. The authors thank the referees for their careful reading and suggestions which led to an improvement of the work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
We declare that all authors collaborated and dedicated the same amount of time in order to perform this article.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pereira, J.V., Silva, R.P. Reaction-diffusion equations in a noncylindrical thin domain. Bound Value Probl 2013, 248 (2013). https://doi.org/10.1186/1687-2770-2013-248
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-248