Existence of symmetric positive solutions for a multipoint boundary value problem with sign-changing nonlinearity on time scales

Fatma Tokmak; Ilkay Yaslan Karaca

doi:10.1186/1687-2770-2013-52

Impact Factor 0.819

Research

Open Access

Existence of symmetric positive solutions for a multipoint boundary value problem with sign-changing nonlinearity on time scales

Fatma Tokmak¹ and
Ilkay Yaslan Karaca¹Email author

Boundary Value Problems20132013:52

https://doi.org/10.1186/1687-2770-2013-52

Received: 30 September 2012

Accepted: 12 February 2013

Published: 14 March 2013

Abstract

In this paper, we make use of the four functionals fixed point theorem to verify the existence of at least one symmetric positive solution of a second-order m-point boundary value problem on time scales such that the considered equation admits a nonlinear term f whose sign is allowed to change. The discussed problem involves both an increasing homeomorphism and homomorphism, which generalizes the p-Laplacian operator. An example which supports our theoretical results is also indicated.

MSC:34B10, 39A10.

Keywords

symmetric positive solution fixed-point theorem time scales m-point boundary value problem increasing homeomorphism and homomorphism

1 Introduction

The theory of time scales was introduced by Stefan Hilger [1] in his PhD thesis in 1988 in order to unify continuous and discrete analysis. This theory was developed by Agarwal, Bohner, Peterson, Henderson, Avery, etc. [2–5]. Some preliminary definitions and theorems on time scales can be found in books [3, 4] which are excellent references for calculus of time scales.

There have been extensive studies on a boundary value problem (BVP) with sign-changing nonlinearity on time scales by using the fixed point theorem on cones. See [6, 7] and references therein. In [8], Feng, Pang and Ge discussed the existence of triple symmetric positive solutions by applying the fixed point theorem of functional type in a cone.

In [9], Ji, Bai and Ge studied the following singular multipoint boundary value problem:

where $0 < ξ_{1} < ξ_{2} < \dots < ξ_{m - 2} < 1$ , $0 < η_{1} < η_{2} < \dots < η_{m - 2} < 1$ , $ξ_{i} < η_{i}$ , $α_{i} > 0$ for $i = 1, 2, \dots, m - 2$ . By using fixed point index theory [10] and the Legget-Williams fixed point theorem [11], sufficient conditions for the existence of countably many positive solutions are established.

Sun, Wang and Fan [12] studied the nonlocal boundary value problem with p-Laplacian of the form

where $0 \leq t_{1} < ξ_{1} < ξ_{2} < \dots < ξ_{m - 2} < t_{m}$ and $t_{1} < η_{1} < η_{2} < \dots < η_{n} < t_{m} < + \infty$ and $ϵ_{i} > 0$ , $θ_{j} \geq 0$ for $i = 1, 2, \dots, m - 2$ and $j = 1, 2, \dots, n$ . By using the four functionals fixed point theorem and five functionals fixed point theorem, they obtained the existence criteria of at least one positive solution and three positive solutions.

Inspired by the mentioned works, in this paper we consider the following m-point boundary value problem with an increasing homeomorphism and homomorphism:

(1.1)

(1.2)

where

T

is a time scale,

ϕ : R \to R

is an increasing homeomorphism and homomorphism with

ϕ (0) = 0

. A projection

ϕ : R \to R

is called an increasing homeomorphism and homomorphism if the following conditions are satisfied:

(i)

If $x \leq y$ , then $ϕ (x) \leq ϕ (y)$ for all $x, y \in R$ ;
(ii)

ϕ is a continuous bijection and its inverse mapping is also continuous;
(iii)

$ϕ (x y) = ϕ (x) ϕ (y)$ for all $x, y \in R$ , where $R = (- \infty, \infty)$ .

We assume that the following conditions are satisfied:

(H1)

$α_{i} \geq 0$ , $\sum_{i = 1}^{m - 2} α_{i} < 1$ , $0 < ξ_{1} < ξ_{2} < \dots < ξ_{m - 2} < 1 / 2$ , $ξ_{i} + η_{i} = 1$ , $i = 1, 2, \dots, m - 2$ , $1 / 2 \in T$ ;
(H2)

$f \in C ({[0, 1]}_{T} \times [0, \infty) \times (- \infty, \infty), (- \infty, \infty))$ is symmetric on ${[0, 1]}_{T}$ (i.e., $f (t, u, v) = f (1 - t, u, - v)$ for $t \in {[0, 1]}_{T}$ );
(H3)

$h \in C_{l d} ({[0, 1]}_{T}, [0, \infty))$ symmetric on ${[0, 1]}_{T}$ (i.e., $h (t) = h (1 - t)$ for $t \in {[0, 1]}_{T}$ ) and $h (t) \neq 0$ on any subinterval of ${[0, 1]}_{T}$ .

By using four functionals fixed point theorem [5], we establish the existence of at least one symmetric positive solution for BVP (1.1)-(1.2). In particular, the nonlinear term $f (t, x (t), x^{Δ} (t))$ is allowed to change sign. The remainder of this paper is organized as follows. Section 2 is devoted to some preliminary lemmas. We give and prove our main result in Section 3. Section 4 contains an illustrative example. To the best of our knowledge, symmetric positive solutions for multipoint BVP for an increasing homeomorphism and homomorphism with sign-changing nonlinearity on time scales by using four functionals fixed point theorem [5] have not been considered till now. In this paper, we intend to fill in such gaps in the literature.

In this paper, a symmetric positive solution x of (1.1) and (1.2) means a solution of (1.1) and (1.2) satisfying $x > 0$ and $x (t) = x (1 - t)$ , $t \in {[0, 1]}_{T}$ .

2 Preliminaries

To prove the main result in this paper, we will employ several lemmas. These lemmas are based on the BVP

(2.1)

(2.2)

Lemma 2.1 If condition (H1) holds, then for

y \in C_{l d} {[0, 1]}_{T}

, boundary value problem (2.1) and (2.2) has a unique solution

x (t)

\begin{array}{rcl} x (t) & = & - \frac{\sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s + ϕ^{- 1} (A_{y} - \int_{0}^{1} y (τ) \nabla τ)}{\sum_{i = 1}^{m - 2} α_{i}} \\ + \int_{0}^{t} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s \end{array}

(2.3)

or

\begin{array}{rcl} x (t) & = & \frac{ϕ^{- 1} (A_{y}) + \sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s}{\sum_{i = 1}^{m - 2} α_{i}} \\ - \int_{t}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s, \end{array}

(2.4)

where

A_{y}

satisfies

\int_{0}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s = 0 .

(2.5)

Proof Suppose x is a solution of BVP (2.1), (2.2). Integrating (2.1) from 0 to t, we have

x^{Δ} (t) = ϕ^{- 1} (A_{y} - \int_{0}^{t} y (τ) \nabla τ) .

(2.6)

Integrating (2.6) from 0 to t, we get

x (t) = x (0) + \int_{0}^{t} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s,

or integrating the same equation from t to 1, we achieve

x (t) = x (1) - \int_{t}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s .

Using boundary condition (2.2), we get

\begin{array}{rcl} x (t) & = & - \frac{\sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s + ϕ^{- 1} (A_{y} - \int_{0}^{1} y (τ) \nabla τ)}{\sum_{i = 1}^{m - 2} α_{i}} \\ + \int_{0}^{t} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s \end{array}

(2.7)

or

\begin{array}{rcl} x (t) & = & \frac{ϕ^{- 1} (A_{y}) + \sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s}{\sum_{i = 1}^{m - 2} α_{i}} \\ - \int_{t}^{1} ϕ^{- 1} (A_{y} - \int_{0}^{s} y (τ) \nabla τ) Δ s, \end{array}

(2.8)

where $A_{y}$ satisfies (2.5).

On the other hand, it is easy to verify that if x is the solution of (2.3) or (2.4), then x is a solution of BVP (2.1), (2.2). The proof is accomplished. □

Lemma 2.2 If $y (t) \in C_{l d} {[0, 1]}_{T}$ is nonnegative on ${[0, 1]}_{T}$ and $y (t) ≢ 0$ on any subinterval of ${[0, 1]}_{T}$ , then there exists a unique $A_{y} \in (- \infty, + \infty)$ satisfying (2.5). Moreover, there is a unique $σ_{y} \in (0, 1)$ such that $A_{y} = \int_{0}^{σ_{y}} y (τ) \nabla τ$ .

Proof For any

y (t) \in (2.1)

, define

H_{y} (c) = \int_{0}^{1} ϕ^{- 1} (c - \int_{0}^{s} y (τ) \nabla τ) Δ s .

So,

H_{y} : R \to R

is continuous and strictly increasing. It is easy to see that

H_{y} (0) < 0, H_{y} (\int_{0}^{1} y (τ) \nabla τ) > 0 .

Therefore there exists a unique

A_{y} \in (0, \int_{0}^{1} y (τ) \nabla τ) \subset (- \infty, + \infty)

satisfying (2.5). Furthermore, let

F (t) = \int_{0}^{t} y (τ) \nabla τ .

Then

F (t)

is continuous and strictly increasing on

{[0, 1]}_{T}

and

F (0) = 0

,

F (1) = \int_{0}^{1} y (τ) \nabla τ

. Thus

0 = F (0) < A_{y} < F (1) = \int_{0}^{1} y (τ) \nabla τ

implies that there exists a unique $σ_{y} \in (0, 1)$ such that $A_{y} = \int_{0}^{σ_{y}} y (τ) \nabla τ$ . Lemma is proved. □

Remark 2.1 By Lemmas 2.1 and 2.2, the unique solution of BVP (2.1), (2.2) can be rewritten in the form

x (t) = {\begin{matrix} \frac{- 1}{\sum_{i = 1}^{m - 2} α_{i}} [\sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{s}^{σ_{y}} y (τ) \nabla τ) Δ s - ϕ^{- 1} (\int_{σ_{y}}^{1} y (τ) \nabla τ)] \\ + \int_{0}^{t} ϕ^{- 1} (\int_{s}^{σ_{y}} y (τ) \nabla τ) Δ s, 0 \leq t \leq σ_{y}, \\ \frac{- 1}{\sum_{i = 1}^{m - 2} α_{i}} [\sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (\int_{σ_{y}}^{s} y (τ) \nabla τ) Δ s - ϕ^{- 1} (\int_{0}^{σ_{y}} y (τ) \nabla τ)] \\ + \int_{t}^{1} ϕ^{- 1} (\int_{σ_{y}}^{s} y (τ) \nabla τ) Δ s, σ_{y} \leq t \leq 1 . \end{matrix}

(2.9)

Lemma 2.3 Let (H1) hold. If

y \in C_{l d}^{Δ} {[0, 1]}_{T}

is nonnegative on

{[0, 1]}_{T}

and

y (t) ≢ 0

on any subinterval of

{[0, 1]}_{T}

, then the unique solution

x (t)

of BVP (2.1)-(2.2) has the following properties:

(i)

$x (t)$ is concave on ${[0, 1]}_{T}$ ,
(ii)

$x (t) > 0$ ,
(iii)

there exists a unique $t_{0} \in {(0, 1)}_{T}$ such that $x^{Δ} (t_{0}) = 0$ ,
(iv)

$σ_{y} = t_{0}$ .

Proof Suppose that

x (t)

is a solution of BVP (2.1)-(2.2), then

(i)

${(ϕ (x^{Δ}))}^{\nabla} (t) = - y (t) \leq 0$ , $ϕ (x^{Δ})$ is nonincreasing so $x^{Δ} (t)$ is nonincreasing. This implies that $x (t)$ is concave.
(ii)

We have $x^{Δ} (0) = \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) = ϕ^{- 1} (A_{y}) > 0$ and $x^{Δ} (1) = ϕ^{- 1} (A_{y} - \int_{0}^{1} y (s) \nabla (s)) < 0$ . Furthermore, we get

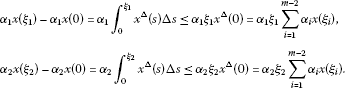
If we continue like this, we have

\begin{array}{rcl} α_{m - 2} x (ξ_{m - 2}) - α_{m - 2} x (0) & = & α_{m - 2} \int_{0}^{ξ_{m - 2}} x^{Δ} (s) Δ s \leq α_{m - 2} ξ_{m - 2} x^{Δ} (0) \\ = & α_{m - 2} ξ_{m - 2} \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) . \end{array}

Using (H1), we obtain

\sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) - \sum_{i = 1}^{m - 2} α_{i} x (0) \leq \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) \sum_{i = 1}^{m - 2} α_{i} ξ_{i} < \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}),

which implies that

x (0) > 0

. Similarly,

If we continue in this way, we attain that

\begin{array}{rcl} α_{m - 2} x (1) - α_{m - 2} x (η_{m - 2}) & = & α_{m - 2} \int_{η_{m - 2}}^{1} x^{Δ} (s) Δ s \geq α_{m - 2} (1 - η_{m - 2}) x^{Δ} (1) \\ = & - α_{m - 2} (1 - η_{m - 2}) \sum_{i = 1}^{m - 2} α_{i} x (η_{i}) . \end{array}

Using (H1), we have

\sum_{i = 1}^{m - 2} α_{i} x (1) > 0

,

x (1) > 0

. Therefore, we get

x (t) > 0

,

t \in {[0, 1]}_{T}

.

(iii)

$x^{Δ} (0) = \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) > 0$ , $x^{Δ} (1) = - \sum_{i = 1}^{m - 2} α_{i} x (η_{i}) < 0$ imply that there is a $t_{0} \in (0, 1)$ such that $x^{Δ} (t_{0}) = 0$ .

If there exist

t_{1}, t_{2} \in (0, 1)

,

t_{1} < t_{2}

, such that

x^{Δ} (t_{1}) = 0 = x^{Δ} (t_{2})

, then

0 = ϕ (x^{Δ} (t_{2})) - ϕ (x^{Δ} (t_{1})) = - \int_{t_{1}}^{t_{2}} y (τ) \nabla τ < 0,

which is a contradiction.

(iv)

From Lemmas 2.1 and 2.2, we have $x^{Δ} (t) = ϕ^{- 1} (\int_{t}^{σ_{y}} y (τ) \nabla τ)$ . Hence we obtain that $x^{Δ} (σ_{y}) = x^{Δ} (t_{0}) = 0$ . This implies $σ_{y} = t_{0}$ .

The lemma is proved. □

Lemma 2.4 If $y (t) \in C_{l d} {[0, 1]}_{T}$ is symmetric nonnegative on ${[0, 1]}_{T}$ and $y (t) ≢ 0$ on any subinterval of ${[0, 1]}_{T}$ , then the unique solution $x (t)$ of (2.1), (2.2) is concave and symmetric with $x (t) \geq 0$ on ${[0, 1]}_{T}$ .

Proof Clearly,

x (t)

is concave and

x (t) \geq 0

from Lemma 2.3. We show that

x (t)

is symmetric on

{[0, 1]}_{T}

. For the symmetry of

y (t)

, it is easy to see that

H_{y} (\int_{0}^{1 / 2} y (τ) \nabla τ) = 0

, i.e.,

σ_{y} = 1 / 2

. Therefore, from (2.9) and for

t \in {[0, 1 / 2]}_{T}

, by the transformation

τ = 1 - \hat{τ}

, we have

\begin{array}{rcl} x (t) & = & \frac{- \sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{s}^{1 / 2} y (τ) \nabla τ) Δ s + ϕ^{- 1} (\int_{1 / 2}^{1} y (τ) \nabla τ)}{\sum_{i = 1}^{m - 2} α_{i}} \\ + \int_{0}^{t} ϕ^{- 1} (\int_{s}^{1 / 2} y (τ) \nabla τ) Δ s \\ = & \frac{\sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{1 - s}^{1 / 2} y (\hat{τ}) \nabla \hat{τ}) Δ s + ϕ^{- 1} (\int_{0}^{1 / 2} y (\hat{τ}) \nabla \hat{τ})}{\sum_{i = 1}^{m - 2} α_{i}} \\ - \int_{0}^{t} ϕ^{- 1} (\int_{1 - s}^{1 / 2} y (\hat{τ}) \nabla \hat{τ}) Δ s . \end{array}

Again, let

s = 1 - \hat{s}

. Then

\begin{array}{rcl} x (t) & = & \frac{- \sum_{i = 1}^{m - 2} α_{i} \int_{1}^{1 - η_{i}} ϕ^{- 1} (\int_{\hat{s}}^{1 / 2} y (\hat{τ}) \nabla \hat{τ}) Δ \hat{s} + ϕ^{- 1} (\int_{0}^{1 / 2} y (\hat{τ}) \nabla \hat{τ})}{\sum_{i = 1}^{m - 2} α_{i}} \\ + \int_{1}^{1 - t} ϕ^{- 1} (\int_{\hat{s}}^{1 / 2} y (\hat{τ}) \nabla \hat{τ}) Δ \hat{s} \\ = & \frac{- \sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} y (τ) \nabla τ) Δ s + ϕ^{- 1} (\int_{0}^{1 / 2} y (τ) \nabla τ)}{\sum_{i = 1}^{m - 2} α_{i}} \\ + \int_{1 - t}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} y (τ) \nabla τ) Δ s \\ = & x (1 - t) . \end{array}

So, $x (t)$ is symmetric on ${[0, 1]}_{T}$ . The proof is accomplished. □

Let

E = C_{l d}^{Δ} {[0, 1]}_{T}

. Then E is a Banach space with the norm

∥ x ∥ = max {sup_{t \in {[0, 1]}_{T}} | x (t) |, sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |} .

We define two cones by

Define the operator

F : P \to E

by

(F x) (t) = {\begin{matrix} \frac{- 1}{\sum_{i = 1}^{m - 2} α_{i}} \sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} ϕ^{- 1} (\int_{1 / 2}^{1} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ + \int_{0}^{t} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s, 0 \leq t \leq 1 / 2, \\ \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} ϕ^{- 1} (\int_{0}^{1 / 2} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ - \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} \sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ + \int_{t}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} h (τ) f (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s, 1 / 2 \leq t \leq 1 \end{matrix}

and

T : K \to E

as follows:

(T x) (t) = {\begin{matrix} \frac{- 1}{\sum_{i = 1}^{m - 2} α_{i}} \sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} ϕ^{- 1} (\int_{1 / 2}^{1} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ + \int_{0}^{t} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s, 0 \leq t \leq 1 / 2, \\ \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} ϕ^{- 1} (\int_{0}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ - \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} \sum_{i = 1}^{m - 2} α_{i} \int_{ξ_{i}}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ + \int_{t}^{1} ϕ^{- 1} (\int_{1 / 2}^{s} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s, 1 / 2 \leq t \leq 1, \end{matrix}

where $f^{+} (t, x (t), x^{Δ} (t)) = max {f (t, x (t), x^{Δ} (t)), 0}$ . Obviously, x is a solution of BVP (2.1)-(2.2) if and only if x is a fixed point of the operator F.

Lemma 2.5 If (H1) holds, then

{sup}_{t \in {[0, 1]}_{T}} x (t) \leq M {sup}_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |

for

x \in K

, where

M = 1 + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} .

(2.10)

Proof For

x \in K

, one arrives at

0 = x (1) - x (0) \leq \frac{x (ξ_{i}) - x (0)}{ξ_{i}},

i.e.,

x (ξ_{i}) \geq x (0)

. Hence,

\sum_{i = 1}^{m - 2} α_{i} x (ξ_{i}) \geq \sum_{i = 1}^{m - 2} α_{i} x (0) .

By

x^{Δ} (0) = \sum_{i = 1}^{m - 2} α_{i} x (ξ_{i})

, we get

x (0) \leq \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} x^{Δ} (0) .

Hence

\begin{array}{rcl} x (t) & = & \int_{0}^{t} x^{Δ} (s) Δ s + x (0) \leq t x^{Δ} (0) + x (0) \leq t x^{Δ} (0) + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} x^{Δ} (0) \\ \leq & (1 + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}}) x^{Δ} (0) = M x^{Δ} (0), \end{array}

i.e.,

sup_{t \in {[0, 1]}_{T}} x (t) \leq M x^{Δ} (0) = M sup_{t \in {[0, 1]}_{T}} x^{Δ} (t) \leq M sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) | .

The proof is finalized. □

From Lemma 2.5, we obtain

\begin{array}{rcl} ∥ x ∥ & = & max {sup_{t \in {[0, 1]}_{T}} | x (t) |, sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |} \\ \leq & max {M sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |, sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |} \\ \leq & M sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) | . \end{array}

Lemma 2.6 Suppose that (H1)-(H3) hold, then $T : K \to K$ is completely continuous.

Proof Let $x \in K$ . According to the definition of T and Lemma 2.3, it follows that ${(ϕ ({(T x)}^{Δ}))}^{\nabla} (t) \leq 0$ , which implies the concavity of $(T x) (t)$ on ${[0, 1]}_{T}$ . On the other hand, from the definition of f and h, $(T x) (t) = (T x) (1 - t)$ holds for $t \in {[0, 1 / 2]}_{T}$ , i.e., Tx is symmetric on ${[0, 1]}_{T}$ . So, $T K \subset K$ . By applying the Arzela-Ascoli theorem on time scales, we can obtain that $T (K)$ is relatively compact. In view of the Lebesgue convergence theorem on time scales, it is obvious that T is continuous. Hence, $T : K \to K$ is a completely continuous operator. The proof is completed. □

3 Existence of one symmetric positive solution

Let α and Ψ be nonnegative continuous concave functionals on P, and let β and θ be nonnegative continuous convex functionals on P, then for positive numbers r, j, n and R, we define the sets:

(3.1)

Theorem 3.1 [5]

If P is a cone in a real Banach space E, α and Ψ are nonnegative continuous concave functionals on P, β and θ are nonnegative continuous convex functionals on P and there exist positive numbers r, j, n and R such that

A : Q (α, β, r, R) \to P

is a completely continuous operator, and

Q (α, β, r, R)

is a bounded set. If

(i)

${x \in U (Ψ, j) : β (x) < R} \cap {x \in V (θ, n) : r < α (x)} \neq \emptyset$ ;
(ii)

$α (A x) \geq r$ for all $x \in Q (α, β, r, R)$ , with $α (x) = r$ and $n < θ (A x)$ ;
(iii)

$α (A x) \geq r$ for all $x \in V (θ, n)$ , with $α (x) = r$ ;
(iv)

$β (A x) \leq R$ for all $x \in Q (α, β, r, R)$ , with $β (x) = R$ and $Ψ (A x) < j$ ;
(v)

$β (A x) \leq R$ for all $x \in U (Ψ, j)$ , with $β (x) = R$ .

Then A has a fixed point x in $Q (α, β, r, R)$ .

Suppose

ω, z \in T

with

0 < ω < z < 1 / 2

. For the convenience, we take the notations

Ω = \int_{w}^{z} h (τ) \nabla τ, Λ = \int_{0}^{1} h (τ) \nabla τ, L = \frac{\sum_{i = 1}^{m - 2} α_{i}}{1 - \sum_{i = 1}^{m - 2} α_{i} ξ_{i} η_{i}}

and define the maps

α (x) = min_{t \in {[ω, z]}_{T}} x (t), θ (x) = max_{t \in {[0, 1]}_{T}} x (t), β (x) = Ψ (x) = sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) |

(3.2)

and let $Q (α, β, r, R)$ , $U (Ψ, j)$ and $V (θ, n)$ be defined by (3.1).

Theorem 3.2 Assume (H1)-(H3) hold. If there exist constants r, j, n, R with $max {\frac{r}{2 ω}, R} \leq n$ , $max {\frac{L + 1}{L} j, \frac{L + 1}{L ω (1 - ω) + 1} r} < R$ and suppose that f satisfies the following conditions:

(C1)

$f (t, u, v) \geq \frac{1}{Ω} ϕ (\frac{r}{ω})$ for $(t, u, v) \in {[ω, z]}_{T} \times [r, n] \times [- R, R]$ ;
(C2)

$f (t, u, v) \leq \frac{1}{Λ} ϕ (R)$ for $(t, u, v) \in {[0, 1]}_{T} \times [0, M R] \times [j, R]$ ;
(C3)

$f (t, u, v) \geq 0$ for $(t, u, v) \in {[0, 1]}_{T} \times [0, M R] \times [- R, R]$ .

Then BVP (1.1)-(1.2) has at least one symmetric positive solution

x \in P

such that

min_{t \in {[ω, z]}_{T}} x (t) \geq r, max_{t \in {[0, 1]}_{T}} x (t) \leq R .

Proof Boundary value problem (1.1)-(1.2) has a solution $x = x (t)$ if and only if x solves the operator equation $x = T x$ . Thus we set out to verify that the operator T satisfies four functionals fixed point theorem, which will prove the existence of a fixed point of T.

We first show that

Q (α, β, r, R)

is bounded and

T : Q (α, β, r, R) \to K

is completely continuous. For all

x \in Q (α, β, r, R)

with Lemma 2.5, we have

∥ x ∥ \leq M sup_{t \in {[0, 1]}_{T}} | x^{Δ} (t) | = M β (x) \leq M R,

which means that $Q (α, β, r, R)$ is a bounded set. According to Lemma 2.6, it is clear that $T : Q (α, β, r, R) \to K$ is completely continuous.

Let

x_{0} = \frac{R}{L + 1} (L t (1 - t) + 1) .

Clearly,

x_{0} \in K

. By direct calculation,

So, $x_{0} \in {x \in U (Ψ, j) : β (x) < R} \cap {x \in V (θ, n) : r < α (x)}$ , which means that (i) in Theorem 3.1 is satisfied.

For all

x \in Q (α, β, r, R)

, with

α (x) = r

and

n < θ (T x)

, we have from concavity

α (T x) = T x (ω) \geq \frac{ω}{1 / 2} T x (1 / 2) = 2 ω θ (T x) > 2 ω n \geq r .

So, $α (T x) > r$ . Hence (ii) in Theorem 3.1 is fulfilled.

For all

x \in V (θ, n)

, with

α (x) = r

,

\begin{array}{rcl} α (T x) & = & min_{t \in {[ω, z]}_{T}} T x (t) = (T x) (ω) \\ = & \frac{- 1}{\sum_{i = 1}^{m - 2} α_{i}} \sum_{i = 1}^{m - 2} α_{i} \int_{0}^{η_{i}} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ + \frac{1}{\sum_{i = 1}^{m - 2} α_{i}} ϕ^{- 1} (\int_{1 / 2}^{1} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ + \int_{0}^{ω} ϕ^{- 1} (\int_{s}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ \geq & \int_{0}^{ω} ϕ^{- 1} (\int_{ω}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) Δ s \\ = & ω ϕ^{- 1} (\int_{ω}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ \geq & ω ϕ^{- 1} (\int_{ω}^{z} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ \geq & ω ϕ^{- 1} (\frac{1}{Ω} ϕ (\frac{r}{ω}) \int_{ω}^{z} h (τ) \nabla τ) = r \end{array}

and for all

x \in U (Ψ, j)

, with

β (x) = R

,

\begin{array}{rcl} β (T x) & = & max_{t \in {[0, 1]}_{T}} | {(T x)}^{Δ} (t) | = {(T x)}^{Δ} (0) \\ = & ϕ^{- 1} (\int_{0}^{1 / 2} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ \leq & ϕ^{- 1} (\int_{0}^{1} h (τ) f^{+} (τ, x (τ), x^{Δ} (τ)) \nabla τ) \\ \leq & ϕ^{- 1} (\frac{1}{Λ} ϕ (R) \int_{0}^{1} h (τ) \nabla τ) = R . \end{array}

Thus (iii) and (v) in Theorem 3.1 hold true. We finally prove that (iv) in Theorem 3.1 holds.

For all

x \in Q (α, β, r, R)

, with

β (x) = R

and

Ψ (T x) < j

, we have

β (T x) = Ψ (T x) < j < \frac{L}{L + 1} R < R .

Thus, all conditions of Theorem 3.1 are satisfied. T has a fixed point x in $Q (α, β, r, R)$ . Clearly, $0 \leq x (t) \leq M R$ , $t \in {[0, 1]}_{T}$ . By condition (C3), we have $f (t, x (t), x^{Δ} (t)) \geq 0$ , $t \in {[0, 1]}_{T}$ , that is, $f^{+} (t, x (t), x^{Δ} (t)) = f (t, x (t), x^{Δ} (t))$ . Hence, $F x = T x$ . This means that x is a fixed point of the operator F. Therefore, BVP (1.1)-(1.2) has at least one symmetric positive solution. The proof is completed. □

4 An example

Example 4.1 Let

T = [0, \frac{1}{3}] \cup {\frac{1}{2}} \cup [\frac{2}{3}, 1]

. If we choose

m = 3

,

ξ_{1} = \frac{1}{5}

,

η_{1} = \frac{4}{5}

,

α_{1} = \frac{1}{3}

,

h (t) = 1

in boundary value problem (1.1)-(1.2), then we have the following BVP on time scale

T

:

{\begin{matrix} {(ϕ (x^{Δ}))}^{\nabla} (t) + f (t, x (t), x^{Δ} (t)) = 0, t \in {[0, 1]}_{T}, \\ x^{Δ} (0) - \frac{1}{3} x (\frac{1}{5}) = 0, x^{Δ} (1) + \frac{1}{3} x (\frac{4}{5}) = 0, \end{matrix}

(4.1)

where

ϕ (x) = x

,

(4.2)

Set

ω = \frac{1}{5}

,

z = \frac{1}{4}

. By simple calculation, we get

Ω = \frac{1}{20}, Λ = 1, L = \frac{25}{71}, M = 4 .

Choose

r = \frac{1}{100}

,

n = 10

,

j = 2

and

R = 8

. It is easy to check that

max {\frac{1}{40}, 8} \leq 10

,

max {\frac{192}{25}, \frac{8}{625}} < 8

.

(1)

$f (t, x (t), x^{Δ} (t)) \geq \frac{76}{75} \geq \frac{1}{Ω} ϕ (\frac{r}{ω}) = 1$ for $(t, x (t), x^{Δ} (t)) \in {[\frac{1}{5}, \frac{1}{4}]}_{T} \times [\frac{1}{100}, 10] \times [- 8, 8]$ ;
(2)

$f (t, x (t), x^{Δ} (t)) \leq 2 \leq \frac{1}{Λ} ϕ (R) = 8$ for $(t, x (t), x^{Δ} (t)) \in {[0, 1]}_{T} \times [0, 32] \times [2, 8]$ ;
(3)

$f (t, x (t), x^{Δ} (t)) \geq 0$ for $(t, x (t), x^{Δ} (t)) \in {[0, 1]}_{T} \times [0, 32] \times [- 8, 8]$ .

So, all conditions of Theorem 3.2 hold. Thus, by Theorem 3.2, BVP (4.1) has at least one symmetric positive solution x such that

min_{t \in {[\frac{1}{5}, \frac{1}{4}]}_{T}} x (t) \geq \frac{1}{100}, max_{t \in {[0, 1]}_{T}} x (t) \leq 8 .

Declarations

Authors’ Affiliations

(1)

Department of Mathematics, Ege University

References

Hilger S: Analysis on measure chains - a unified approach to continuous and discrete calculus. Results Math. 1990, 18: 18-56. 10.1007/BF03323153MATHMathSciNetView ArticleGoogle Scholar
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results Math. 1999, 35: 3-22. 10.1007/BF03322019MATHMathSciNetView ArticleGoogle Scholar
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston; 2001.View ArticleGoogle Scholar
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston; 2003.MATHView ArticleGoogle Scholar
Avery R, Henderson J, O’Regan D: Four functionals fixed point theorem. Math. Comput. Model. 2008, 48: 1081-1089. 10.1016/j.mcm.2007.12.013MATHMathSciNetView ArticleGoogle Scholar
Hamal NA, Yoruk F: Symmetric positive solutions of fourth order integral BVP for an increasing homeomorphism and homomorphism with sign-changing nonlinearity on time scales. Comput. Math. Appl. 2010, 59: 3603-3611. 10.1016/j.camwa.2010.03.056MATHMathSciNetView ArticleGoogle Scholar
Xu F, Meng Z: The existence of positive solutions for third-order p -Laplacian m -point boundary value problems with sign changing nonlinearity on time scales. Adv. Differ. Equ. 2009., 2009: Article ID 169321Google Scholar
Feng H, Pang H, Ge W: Multiplicity of symmetric positive solutions for a multipoint boundary value problem with a one-dimensional p -Laplacian. Nonlinear Anal. 2008, 69: 3050-3059. 10.1016/j.na.2007.08.075MATHMathSciNetView ArticleGoogle Scholar
Ji D, Bai Z, Ge W: The existence of countably many positive solutions for singular multipoint boundary value problems. Nonlinear Anal. 2010, 72: 955-964. 10.1016/j.na.2009.07.031MATHMathSciNetView ArticleGoogle Scholar
Deimling K: Nonlinear Functional Analysis. Springer, New York; 1985.MATHView ArticleGoogle Scholar
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana Univ. Math. J. 1979, 28: 673-688. 10.1512/iumj.1979.28.28046MATHMathSciNetView ArticleGoogle Scholar
Sun TT, Wang LL, Fan YH: Existence of positive solutions to a nonlocal boundary value problem with p -Laplacian on time scales. Adv. Differ. Equ. 2010., 2010: Article ID 809497Google Scholar

Copyright

This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.