- Research
- Open access
- Published:
Existence of periodic solutions for a class of p-Laplacian equations
Boundary Value Problems volume 2013, Article number: 96 (2013)
Abstract
This paper is devoted to the existence of periodic solutions for the one-dimensional p-Laplacian equation
where (), . By using some asymptotic interaction of the ratios and with the Fučík spectrum of related to periodic boundary condition, we establish a new existence theorem of periodic solutions for the one-dimensional p-Laplacian equation.
1 Introduction and main results
In this paper, we are concerned with the existence of solutions for the following periodic boundary value problem:
where (), . A solution u of problem (1.1) means that u is and is absolutely continuous such that (1.1) is satisfied for a.e. .
Existence and multiplicity of solutions of the periodic problems driven by the p-Laplacian have been obtained in the literature by many people (see [1–5]). Many solvability conditions for problem (1.1) were established by using the asymptotic interaction at infinity of the ratio with the Fučík spectrum for under periodic boundary condition (see e.g., [2, 4, 6–9]). In [6], Del Pino, Manásevich and Murúa firstly defined the Fučík spectrum for under periodic boundary value condition as the set consisting of all the pairs such that the equation
admits at least one nontrivial 2π-periodic solution (see [10] for ). Let
By [6], it follows that
Then they applied the Sturm’s comparison theorem and Leray-Schauder degree theory to prove that problem (1.1) is solvable if the following relations hold:

uniformly for a.e. with satisfying
Clearly, in this case, we have , which is usually called that the nonlinearity f is nonresonant with respect to the Fučík spectrum . In [11], Anane and Dakkak obtained a similar result by using the property of nodal set for eigenfunctions. If f is resonant with respect to , i.e., there exists such that , uniformly for a.e. , together with the Landesman-Lazer type condition, Jiang [9] obtained the existence of solutions of (1.1) by applying the variational methods and symplectic transformations. In these works, either f is resonant or nonresonant with respect to , the solvability of problem (1.1) was assured by assuming that the ratio stays at infinity in the pointwise sense asymptotically between two consecutive curves of . Note that
we can see that the conditions on the ratio are more general than that on the ratio . Recently, Liu and Li [2] studied the nondissipative p-Laplacian equation
where is a constant. Define . They proved that (1.2) is solvable under the following assumptions:
-
(1)
There exist such that for all ;
-
(2)
, with .
Here, the potential function G is nonresonant with respect to and the ratio is not required to stay at infinity in the pointwise sense asymptotically between two consecutive branches of and it may even cross at infinity multiple Fučík spectrum curves.
In this paper, we want to obtain the solvability of problem (1.1) by using the asymptotic interaction at infinity of both the ratios and with the Fučík spectrum for under periodic boundary condition. Here, . The goal is to obtain the existence of solutions of (1.1) by requiring neither the ratio stays at infinity in the pointwise sense asymptotically between two consecutive branches of nor the limits exist. We shall prove that problem (1.1) admits a solution under the assumptions that the nonlinearity f has at most -linear growth at infinity and the ratio has a limit as , while the ratio stays at infinity in the pointwise sense asymptotically between two consecutive branches of . Our result will complement the results in the literature on the solvability of problem (1.1) involving the Fučík spectrum.
For related works on resonant problems involving the Fučík spectrum, we also refer the interested readers to see [12–19] and the references therein.
Our main result for problem (1.1) now reads as follows.
Theorem 1.1 Assume that and the following conditions hold:
-
(i)
There exist constants such that
(1.3) -
(ii)
There exists such that
(1.4) -
(iii)
There exist constants such that
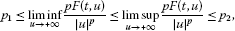 (1.5)
(1.5)

hold uniformly for a.e. with
Then problem (1.1) admits a solution.
Remark If , where with , and satisfy (1.7), e is continuous on ℝ and , then and . By Theorem 1.1, it follows that problem (1.1) admits a solution. It is easily seen that the result of [16] cannot be applied to this case. Note that one can also obtain the solvability of (1.1) in this case by the result of [6], while in Theorem 1.1 we do not require the pointwise limit at infinity of the ratio as in [6].
For convenience, we introduce some notations and definitions. () denotes the usual Sobolev space with inner product and norm , respectively. () denotes the space of m-times continuous differential real functions with norm
2 Proof of the main result
Denote by deg the Leray-Schauder degree. To prove Theorem 1.1, we need the following results.
Lemma 2.1 [20]
Let Ω be a bounded open region in a real Banach space X. Assume that is completely continuous and . Then the equation has a solution in Ω if .
Lemma 2.2 (Borsuk Theorem [20])
Assume that X is a real Banach space. Let Ω be a symmetric bounded open region with . Assume that is completely continuous and odd with . Then is odd.
Proof of Theorem 1.1 Take . Consider the following homotopy problem:
where .
By (1.3) and the regularity arguments, it follows that , and furthermore there exists such that, if u is a solution of problem (2.1), then
In what follows, we shall prove that there exists independent of such that for all possible solution of (2.1). Assume by contradiction that there exist a sequence of number and corresponding solutions of (2.1) such that
Set . Obviously, . Define
and
By (1.3), there exists such that
Then there exist such that
In addition, using (1.3) and the regularity arguments, there exists such that, for each n, we have , and thus there exists such that, passing to a subsequence if possible,
Clearly, . In view of , there exists such that, passing to a subsequence if possible,
Note that for , problem (2.1) has only the trivial solution, it follows that . Denote , . It is easily seen that is a nontrivial solution of the following problem:
We now distinguish three cases:
-
(i)
changes sign in ;
-
(ii)
, ;
-
(iii)
, .
In the following, it will be shown that each case leads to a contradiction.
Case (i). Let

Then, as , we get

In addition, as shown in [11], we have . Define
and
By (1.4) and (2.4), it follows that
Thus, satisfies
Here, , .
Now we prove that there exist and such that
In fact, if not, we assume, by contradiction, that there exists a subsequence of , we still denote it as with and , such that
Combing with (2.5), and the fact that changes sign, we obtain
A contradiction. Hence, (2.9) holds.
For any , define

and
Denote , . Then by (2.9) it follows that and . Taking such that , is the nearest point satisfying and . Since , there exist such that
By (2.5), we obtain , . Note that , we have , . Hence, together with and (1.4), there exist subsequences of and , we still denote them as and , such that, for a.e. ,
Using (1.3), for a.e. , is uniformly bounded with respect to , we obtain by the Lebesgue dominated convergence theorem that
Thus,

By (1.4) and (2.2), we get

In view of (2.11), we obtain that
holds uniformly for a.e. . Similarly,
holds uniformly for a.e. .
On the other hand, for , satisfying (2.12)-(2.13), denoting

we obtain by (1.5)-(1.6) that
Using , we have


We claim that there exists subinterval with such that
or subinterval with such that
Indeed, if not, we assume that , , a.e. . Together with the choosing of , and (2.14), we get
Then by (1.7), it follows that . A contradiction. Combining (2.12)-(2.13) with (2.15)-(2.18), we obtain a contradiction.
Case (ii). In this case, we have
Using similar arguments as in Case (i), by (1.4) and (2.4) it follows that , . Taking , , a.e. . We can see that there exists subsequence of , which is still denoted by , such that
holds uniformly for a.e. . On the other hand, for satisfying (2.19), denoting
we obtain by (1.5) that
Using , we have

We shall show that there exists subinterval with such that
In fact, if not, we assume that , a.e. . By the choosing of and (2.20), we get , a.e. . Thus, is a nontrivial solution of the following problem:
Taking 1 as test function in problem (2.23), we get
By for a.e. , it follows that for a.e. , which is contrary to that . Hence, (2.22) holds. Clearly, (2.21)-(2.22) contradict (2.19).
Case (iii). In this case, and is uniformly bounded. Similar arguments as in Case (ii) imply a contradiction.
In a word, (2.3) cannot hold, and hence by (2.2) there exists independent of such that, if u is a solution of problem (2.1), then
Note that, for each , the problem
has a unique solution . Clearly, the operator seen as an operator from into is completely continuous. Define by . Then solving problem (1.1) is equivalent to finding solutions in of the equation
Let . Define the operator by . Denote . Clearly, is well defined for all . Owing to , there is a continuous curve , , , whose image is in and such that , . From the invariance property of Leray-Schauder degree under compact homotopies, it follows that the degree is constant for . Obviously, the operator is odd. By the Borsuk’s theorem, it follows that for all . Thus,
Consider the following homotopy:
for . By (2.25), we can see that there exists such that
From the invariance property of Leray-Schauder degree, it follows that
Hence, problem (1.1) has a solution. The proof is complete. □
References
Aizicovici S, Papageorgiou NS, Staicu V: Nonlinear resonant periodic problems with concave terms. J. Math. Anal. Appl. 2011, 375: 342-364. 10.1016/j.jmaa.2010.09.009
Liu W, Li Y: Existence of periodic solutions for p -Laplacian equation under the frame of Fučík spectrum. Acta Math. Sin. Engl. Ser. 2011, 27: 545-554. 10.1007/s10114-011-9719-1
Manásevich R, Mawhin J: Periodic solutions for nonlinear systems with p -Laplacian-like operators. J. Differ. Equ. 1998, 145: 367-393. 10.1006/jdeq.1998.3425
Reichel W, Walter W: Sturm-Liouville type problems for the p -Laplacian under asymptotic nonresonance conditions. J. Differ. Equ. 1999, 156: 50-70. 10.1006/jdeq.1998.3611
Yang X, Kim Y, Lo K: Periodic solutions for a generalized p -Laplacian equation. Appl. Math. Lett. 2012, 25: 586-589. 10.1016/j.aml.2011.09.064
Del Pino M, Manásevich R, Murúa A: Existence and multiplicity of solutions with prescribed period for a second order quasilinear ODE. Nonlinear Anal. 1992, 18: 79-92. 10.1016/0362-546X(92)90048-J
Fabry C, Fayyad D: Periodic solutions of second order differential equations with a p -Laplacian and asymmetric nonlinearities. Rend. Ist. Mat. Univ. Trieste 1992, 24: 207-227.
Fabry C, Manásevich R: Equations with a p -Laplacian and an asymmetric nonlinear term. Discrete Contin. Dyn. Syst. 2001, 7: 545-557.
Jiang M: A Landesman-Lazer type theorem for periodic solutions of the resonant asymmetric p -Laplacian equation. Acta Math. Sin. 2005, 21: 1219-1228. 10.1007/s10114-004-0459-3
Drábek P Pitman Research Notes in Mathematics 264. Solvability and Bifurcations of Nonlinear Equations 1992.
Anane A, Dakkak A: Nonexistence of nontrivial solutions for an asymmetric problem with weights. Proyecciones 2000, 19: 43-52.
Boccardo L, Drábek P, Giachetti D, Kućera M: Generalization of Fredholm alternative for nonlinear differential operators. Nonlinear Anal. 1986, 10: 1083-1103. 10.1016/0362-546X(86)90091-X
Drábek P, Invernizzi S: On the periodic boundary value problem for forced Duffing equation with jumping nonlinearity. Nonlinear Anal. 1986, 10: 643-650. 10.1016/0362-546X(86)90124-0
Fonda A: On the existence of periodic solutions for scalar second order differential equations when only the asymptotic behaviour of the potential is known. Proc. Am. Math. Soc. 1993, 119: 439-445. 10.1090/S0002-9939-1993-1154246-4
Habets P, Omari P, Zanolin F: Nonresonance conditions on the potential with respect to the Fučík spectrum for the periodic boundary value problem. Rocky Mt. J. Math. 1995, 25: 1305-1340. 10.1216/rmjm/1181072148
Liu W, Li Y: Existence of 2 π -periodic solutions for the non-dissipative Duffing equation under asymptotic behaviors of potential function. Z. Angew. Math. Phys. 2006, 57: 1-11.
Omari P, Zanolin F: Nonresonance conditions on the potential for a second-order periodic boundary value problem. Proc. Am. Math. Soc. 1993, 117: 125-135. 10.1090/S0002-9939-1993-1143021-2
Zhang M: Nonresonance conditions for asymptotically positively homogeneous differential systems: the Fučík spectrum and its generalization. J. Differ. Equ. 1998, 145: 332-366. 10.1006/jdeq.1997.3403
Zhang M: The rotation number approach to the periodic Fučík spectrum. J. Differ. Equ. 2002, 185: 74-96. 10.1006/jdeq.2002.4168
Deimling K: Nonlinear Functional Analysis. Springer, New York; 1985.
Acknowledgements
The first author sincerely thanks Professor Yong Li and Doctor Yixian Gao for their many useful suggestions and the both authors thank Professor Zhi-Qiang Wang for many helpful discussions and his invitation to Chern Institute of Mathematics. The first author is partially supported by the NSFC Grant (11101178), NSFJP Grant (201215184) and FSIIP of Jilin University (201103203). The second author is partially sup- ported by NSFC Grant (11226123).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chang, X., Qiao, Y. Existence of periodic solutions for a class of p-Laplacian equations. Bound Value Probl 2013, 96 (2013). https://doi.org/10.1186/1687-2770-2013-96
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-96