- Research
- Open access
- Published:
On the stability of Rayleigh–Taylor problem for stratified rotating viscoelastic fluids
Boundary Value Problems volume 2018, Article number: 122 (2018)
Abstract
We investigate the stability of Rayleigh–Taylor (RT) problem of the stratified incompressible viscoelastic fluids under the rotation and the gravity in a horizontal periodic domain, in which the rotation axis is parallel to the direction of gravity, the two fluids are immiscible, and the heavier fluid lies on the lighter one. We establish a stability condition for the RT problem. Moreover, we prove that, under the stability condition, the RT problem enjoys a unique strong solution, which exponentially decays with respect to time. In addition, we note that the stability condition is independent of rotation angular velocity, and the rotation has no destabilizing effect.
1 Introduction
Considering two completely plane-parallel layers of immiscible fluids, the heavier on top of the lighter one and both subject to the earth’s gravity, it is well-known that such equilibrium state is unstable to sustain small disturbances, and this unstable disturbance will grow and lead to a release of potential energy as the heavier fluid moves down under the gravitational force and the lighter one is displaced upwards. This phenomenon was first studied by Rayleigh [33] and then Taylor [34], and therefore is called the Rayleigh–Taylor (RT) instability. In the last decades, this phenomenon has been extensively investigated from both physical and numerical aspects, see [3, 8, 17, 19, 23, 36] for examples. It has been also widely investigated how the RT instability evolves under the effects of other physical factors, internal surface tension [9, 38], magnetic fields [3, 4, 18, 21, 22, 24, 25], and so on.
Recently, Jiang et al. [16, 27] have found that the elasticity can inhibit the RT instability based on the following idea, i.e., Oldroyd–B model of an incompressible viscoelastic fluid in the presence of a uniform gravitational field in a three-dimensional domain Ω:
Here \(\mathbf {v}:=\mathbf{v}(t,{x})\), \(p:=p(t,{x})\), and \({U}:={U}(t,{x})\) represent velocity, pressure, and deformation tensor (a \(3\times3\) matrix-valued function), respectively. \(\rho, \mu >0\), \(\kappa>0\), \(g>0\) stand for the density, viscosity coefficient, elasticity coefficient, and gravitational constant, respectively. \({e}_{3}:=(0,0,1)^{\mathrm{T}}\) is the vertical unit vector, and \(-g{e}_{3}\) denotes the gravitational force. We mention that the well-posedness problem of (1.1) without gravity \(-\rho ge_{3}\) has been widely studied, see [28–31] for examples, the corresponding compressible case has also been investigated in [11–15].
Recently, Baldwin et al. investigated the effect of rotation on the RT instability by an experiment. Motivated by the experiment of Baldwin et al. and the mathematical result of Jiang et al. [16, 27], we further mathematically investigate the effect of rotation on the RT instability in the stratified viscoelastic fluids in this article. Before stating our result, we shall introduce the mathematical model.
1.1 Stratified rotating VRT problem in Eulerian coordinates
We consider the stratified incompressible viscoelastic fluids under the rotation and the gravity in a layer domain, in which the rotation axis is parallel to the direction of gravity. Moreover, the two fluids are immiscible, and the heavier fluid lies on the lighter one. Referring to the motion equations (1.1) and the motion equations of stratified viscous fluids (see [20]), we can easily write out the mathematical model of stratified viscoelastic fluids without internal surface tension:
where \(\mathbb {S}(p_{\pm}^{g},\mathbf {v}_{\pm}, U_{\pm}):=p_{\pm}^{g} I-\mu_{\pm}\mathbb {D}(\mathbf {v}_{\pm})-\kappa_{\pm}\rho_{\pm}(U_{\pm}U_{\pm}^{T}-I)\) and \(p_{\pm}^{g}:=p_{\pm}+g\rho_{\pm}x_{3}\). Next we shall introduce the notations appearing in the above mathematical model.
Equations (1.2)1–(1.2)2 describe the motion of the lower lighter and upper heavier viscoelastic fluids driven by the gravitational field along the negative \(x_{3}\)-direction, which occupy the two time-dependent disjoint open subsets \(\Omega_{+}(t)\) and \(\Omega_{-}(t)\) at time t, respectively. The fluids are incompressible by (1.2)3. The two fluids interact with each other by the interfacial jump conditions (1.2)5 and the motion of a free interface (1.2)4, in which \(d:=d(x_{1},x_{2},t)\) represents the displacement function of the point at the interface. (1.2)6 describes the non-slip boundary condition of the velocities on both upper and lower fixed flat boundaries, and the initial statuses of the two fluids are described by (1.2)7–(1.2)8.
The notations \(f_{-}\) and \(f_{+}\) in (1.2) denote the values of the quantity f in the lower and upper fluids, respectively. The term \(2\rho_{\pm}(\mathbf {a}\times\mathbf {v}_{\pm})\) represents the Coriolis force with constant rotation angular velocity \(\mathbf{a}=(0,0,a)\) about the vertical direction [5]. \(\mathbb {D}(\mathbf {v}_{\pm}):=\nabla\mathbf {v}_{\pm}+(\nabla\mathbf {v}_{\pm})^{\mathrm{T}}\) denotes viscous stress tension. The superscript T and the capital letter I stand for the transposition and the \(3\times3\) identity matrix, respectively. The notations \(f^{0}\) or \(f_{0}\) represent the initial data of f.
In this article, we consider that the domain Ω occupied by the two fluids is horizontal periodic, thus we denote

where we have defined that \(\mathbb{T}_{i}=2\pi L_{i}(\mathbb{R}/\mathbb {Z})\) and \(\mathbb{T}=\mathbb{T}_{1}\times\mathbb{T}_{2}\). Moreover, we have the following expressions:
Finally, we explain the interfacial jump conditions (1.2)5. The mathematical notation represents
where \(f_{\pm}|_{\Sigma(t)}\) denote the traces of the quantities \(f_{\pm}\) on \(\Sigma(t)\). From the physical point of view, the velocity of two viscous fluids meeting at a free boundary is continuous across the interface and the jump in the normal stress is proportional to the mean curvature of the surface multiplied by the normal to the surface (see [38]). Thus, we have the jump conditions on \(\Sigma(t)\) and
where we have defined that
and ν represents the unit normal vector on \(\Sigma(t)\), ϑ the surface tension coefficient, and \(\mathcal{C}\) twice the mean curvature of the internal surface \(\Sigma(t)\). Here we only focus on the elasticity effect upon the RT instability, then the surface tension is omitted. Thus we obtain the second jump condition in (1.2)5. In addition, since the density of the lower fluid is lighter than the upper one, we have
Problem (1.2) enjoys the following stratified equilibrium state solution:
where \(\bar{d}\in(-l,m)\). We should point out that \(\bar{p}^{g}\) can be uniquely computed out by hydrostatics, which depends on the variable \(x_{3}\) and \(\rho_{\pm}\) and is continuous with respect to \(x_{3}\in (-l,m)\). Without loss of generality, we assume that \(\bar{d}=0\) in this article. If d̄ is not zero, we can adjust the \(x_{3}\) coordinate to make \(\bar{d}=0\). Thus d can be regarded as a displacement function away from the plane
To simplify problem (1.2), we introduce the indicator function χ:
Then we define that
and denote the perturbation quantity around the equilibrium state \((0,I,0,\bar{p}^{g})\) by
Thus we have the following perturbation form for problem (1.2):

where \(\Sigma_{-}^{+}:=\Sigma_{+}\cup\Sigma_{-}\), and \(\mathbb {S}(\sigma, \mathbf {v},V+I)\) is defined by (1.4) with \((\sigma, \mathbf {v},V+I)\) in place of \((p_{\pm}, \mathbf {v}_{\pm},U_{\pm})\). Here and in what follows, the subscript ± has been omitted in the jump notation for simplicity. Thus the equilibrium-state solution of (1.5) is \((\mathbf {v} ,V,d,\sigma)=(0,0,0,0)\). In this article, we call the initial-boundary value problem (1.5) the stratified rotation viscoelastic Rayleigh–Taylor (SRVRT) problem.
1.2 Reformulation in Lagrangian coordinates
It is difficult to investigate the well-posedness of the SRVRT problem due to the movement of the free interface \(\Sigma(t)\) and the changes of the domain \(\Omega_{\pm}(t)\) in Eulerian coordinates. Therefore we switch the problem to Lagrangian coordinates, so that the interface and the domains stay fixed in time. To this purpose, we define the fixed Lagrangian domains \(\Omega_{+}:=\mathbb {T}\times(0,m)\), \(\Omega_{-}=\mathbb {T}\times(-l,0)\), and \(\Omega:=\Omega_{+}\cup\Omega_{-}\), and assume that there exist invertible mappings
such that
and
The first condition in (1.6) means that the initial interface \(\Sigma(0)\) is parameterized by the mapping \(\xi_{\pm}^{0}\) defined on Σ, while the latter two conditions in (1.6) mean that \(\xi_{\pm}^{0}\) map the fixed upper and lower boundaries into themselves. Let \(\xi_{\pm}\) be the flow maps, which are solutions to
We call \((x,t)\) with \(x=\xi(y,t)\) and \((y,t)\in\Omega\times \mathbb {R}^{+}\) the Eulerian coordinates and Lagrangian coordinates, respectively.
We further assume that \(\xi_{\pm}(\cdot,t)\) are invertible and
in order to switch back from Lagrangian to Eulerian coordinates. Since \(\mathbf {v}_{\pm}\) and \(\xi_{\pm}^{0}\) are all continuous across the surface Σ, we have
In other words, the Eulerian domains of upper and lower fluids are the image of \(\Omega_{\pm}\) under the mapping \(\xi_{\pm}\), and the free interface is the image of Σ under the mappings \(\xi_{\pm}(t,\cdot)\). Recalling the non-slip boundary condition \(\mathbf {v}_{\pm}|_{\Sigma_{\pm}}=0\), we have
Using the incompressible condition, we can derive that
as well as the initial condition (1.7), please refer to [32, Proposition 1.4] for the derivation.
In Lagrangian coordinates, we can use the Jacobi matrix of \(\xi_{\pm}(y,t)\) to define the deformation tensor \(\tilde{U}_{\pm}(y,t)\):
where \(\partial_{j}\) stands for the partial derivative with respect to the jth component of the spatial variables. In Eulerian coordinates, the deformation tensor can be rewritten as follows:
Using the chain rule, it is easy to verify that \(U_{\pm}(x,t)\) enjoys the transport equation
Now, we define \(\xi=\chi_{+}\xi_{+}+\chi_{-}\xi_{-}\), \(\eta=\xi-y\), and the Lagrangian unknowns
then the motion equations of u and q in Lagrangian coordinates the evolution equations read as follows:
where we have defined that
for the unit normal to \(\Sigma(t)=\xi(\Sigma,t)\). Since on Σ, then
Thus the definition of n in (1.12) makes sense. We call problem (1.9) the transformed SRVRT problem. In this article, we prove that the transformed SRVRT problem is stable under proper conditions, see Theorem 2.1.
Next, we further introduce the notations involving \(\mathcal {A}\). The matrix \(\mathcal {A}\) is defined by the relation
We define the differential operator \(\nabla_{\mathcal {A}}\) by
where \(\mathcal {A}_{ij}\) is the \((i,j)\)th entry of \(\mathcal{A}\), \(w:=(w_{1},w_{2},w_{3})^{\mathrm{T}}\), and we have used the Einstein convention of summation over repeated indices. The differential operator \(\operatorname {div}_{\mathcal {A}}\) is defined by
for the vector function \(f_{i}:=(f_{i1},f_{i2},f_{i3})^{T}\). In addition,
Finally, we introduce some properties of \(\mathcal {A}\). Recalling the definition of \(\mathcal {A}\) and (1.8), we have
where \(\mathcal {A}^{*}_{ij}\) represents the algebraic complement minor of the \((i,j)\)th entry of the matrix \((\partial_{j}\xi_{i})_{3\times3}\). In addition, we have
and
where we have defined that \(\delta_{il}=1\) for \(i=l\) and \(\delta _{il}=0\) for \(i\neq l\). Thus
The rest of this paper is organized as follows. In Sect. 2, we present the stability result of the transformed SRVRT problem. Then, in Sect. 3, we deduce some preliminary estimates, while in Sect. 4 we derive a priori estimates of η and u. Finally, in Sect. 5, we derive an exponential decay estimate which, together with the local well-posedness result of the transformed SRVRT problem, yields the desired stability result of the transformed SRVRT problem.
2 Main results
Before stating our main result, we shall derive the stability condition for the transformed SRVRT problem. To begin with, we introduce some notations, which are used throughout this article.
-
(1)
Simplified function spaces:
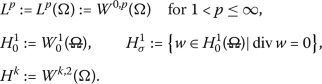
-
(2)
Simplified norms:
-
(3)
Energy and functionals:
-
(4)
Other notations:
$$ \begin{gathered} f\in H^{k+\frac{1}{2}} \text{ denotes } f(y_{h},0)\in H^{k+\frac {1}{2}}(\mathbb {T})\quad \text{for } f=(y_{h},y_{3}), y_{h}=(y_{1},y_{2}), \\ \partial_{h}^{i} \text{ denotes } \partial_{1}^{\alpha_{1}} \partial_{2}^{\alpha _{2}} \quad\text{for any } \alpha_{1}+ \alpha_{2}=i, \\ a\lesssim b\hbox{ means that }a\leq cb,\qquad a\gtrsim b\hbox{ means that }a\geq cb, \end{gathered} $$where the letter c denotes a positive constant depending on the domain and the known physical parameters in the transformed SRVRT problem.
Now we start to derive the stability condition. We assume that \((u,\eta )\) is very small, thus we can neglect the small terms of the second order (i.e., the nonlinear terms) in (1.9) and obtain the following linearized transformed SRVRT problem:
It is convenient to analyze the physical and mathematical mechanisms in the transformed SRVRT problem based on the linearized problem.
Exploiting the standard method, we shall look for the normal mode solutions of (2.1) in the following form:
Inserting these ansatz into (2.1) yields the following eigenvalue problem:
Replacing η̃ by (2.2)1, we arrive at the boundary value problem:
Multiplying (2.3)1 by ũ in \(L^{2}\) and exploiting the formula of integration by parts and conditions (2.3)2–(2.3)4, one has
Noting that
thus we derive that
where we have defined that
Using the point of view of energy, if \(\tilde{E}(\tilde{u})<0\) for some ũ, then the linearized SRVRT problem may be stable. Hence, we have the stability criterion: if \(\mathrm{C}_{\mathrm{r}} <1\) (i.e., the elasticity coefficient κ is appropriately large), any solution to the linearized stratified VRT problem enjoys some stability estimate, where we have defined that
In this article, we will rigorously prove that the transformed SRVRT problem (1.9) is stable. More precisely, we have the following mathematical result.
Theorem 2.1
Let \(a\geq0\). Under the stability condition \(\mathrm{C}_{\mathrm{r}}<1\), there is a sufficiently small constant \(\delta>0\) such that for any \((u_{0},\eta _{0})\in H^{2}\times H^{3}\) enjoying the following conditions:
-
(1)
\(u_{0}=0\) on \(\Sigma_{-}^{+}\) and \(\operatorname {div}_{\mathcal {A}_{0}} u_{0}=0\);
-
(2)
\(\operatorname{det}(\nabla\eta_{0}+I)=1\), \(\eta_{0}=0 \) on \(\Sigma_{-}^{+}\) and on Σ;
-
(3)
\(\|u_{0}\|_{2}+\|\eta_{0}\|_{3}\leq\delta\);
-
(4)
the initial value \((u_{0},\eta_{0})\) satisfies the compatibility condition
then the transformed SRVRT problem (1.9) possesses a unique global solution \((u,\eta)\in C^{0}([0,\infty), H^{2}\times H^{3})\) with an associated perturbation pressure q. Furthermore, \((\eta,u,q)\) has the following exponential stability estimate:
$$ \mathcal {E}(t)\leq c e^{-ct}\bigl( \Vert u_{0} \Vert _{2}^{2}+ \Vert \eta_{0} \Vert _{3}^{2}\bigr), $$(2.7)where \(\mathcal {A}_{0}\) and \(\mathbf {n}_{0}\) denote the initial data of \(\mathcal {A}\) and n, respectively, and are defined by \(\eta_{0}\), and the positive constants δ and c depend on the domain and the physical parameters in the transformed SRVRT problem.
Remark 2.1
In view of the proof of Theorem 2.1, we can easily observe that Theorem 2.1 still holds if \(\Omega=\{x\in \mathbb {R}^{3}|{-}l< x_{3}< m\}\) or one of \(\kappa_{+}\) and \(\kappa _{-}\) is non-zero and sufficiently large. Moreover, if \(\kappa_{+}=\kappa _{-}\), then the stability condition is equivalent to \(\kappa>\kappa_{c}\), where we have defined that
It should be noted that the stability condition is independent of a. Thus Theorem 2.1 presents that the rotation has no destabilizing effect. Next we briefly introduce the proof of Theorem 2.1. The key step of the proof is to deduce an a priori exponential decay estimate (2.7). To this purpose, we naturally construct an energy inequality of differential form
for some energy functional \(\tilde {\mathcal {E}}(t)\) (see (5.7) for the definition) and dissipative functional \(\tilde {\mathcal {D}}(t)\) (see (5.8) for the definition). Moreover, \(\tilde {\mathcal {E}}(t)\) and \(\tilde {\mathcal {D}}(t)\) are equivalent to \(\mathcal{E}(t)\) and \(\mathcal{D}(t)\), respectively, and \(\tilde {\mathcal {E}}(t)\) can be controlled by \(\mathcal{D}(t)\). In particular, if \(\mathcal{E}\) is sufficiently small, we further have
which implies the desired exponential decay estimate by Gronwall’s inequality. Thus, by a local well-posedness result of the transformed SRVRT problem, we immediately get Theorem 2.1.
Here we mention the derivation of (2.8). Recently, Jiang et al. [27] have proved that the elasticity can inhibit the RT instability based on the energy method. To obtain (2.8), we naturally use the energy method in [27] to prove Theorem 2.1. However, we need some more complicated mathematical techniques for the estimate of \(\|\eta\|_{3}\). Thus our derivation of the estimate of \(\|\eta\|_{3}\) is very different with the one in [27]. In fact, since \(w:=u+(\kappa\rho/\mu)\eta\) may not be continuous on Σ, we shall apply the regularity theory of one-phase steady Stokes problem to the momentum equations of upper and lower viscoelastic fluids. Thus we derive an energy inequality of \(\| \eta\|_{3}\), which has some norms of \(y_{h}\)-derivative (i.e., horizontal derivative) of \((u,\eta)\), see Lemma 4.2 for details. Moreover, we also derive a series of energy inequalities of \(y_{h}\)-derivative in the energy inequalities of \(y_{h}\)-derivative of \((u,\eta)\), see Lemmas 4.1 and 4.4 for details, which can close the norms involving \(y_{h}\)-derivative in the energy inequality of \(\|\eta\|_{3}\). Thus, we can still exploit a standard energy method to establish the energy inequality (2.8). It should be noted that \(\tilde {\mathcal {E}}(t)\) contains some negative terms involving gravity. To control the non-positive terms, we shall use the stability condition based on the physical idea that the stabilizing terms of elasticity can control the non-positive term, see Lemma 4.3 for details. Thus we derive the equivalence of \(\tilde {\mathcal {E}}\) and \(\mathcal {E}\). Of course, we will also use the stability condition in the derivation of the dissipative functional \(\mathcal {D}\).
3 Preliminary estimates
The key step in the proof of Theorem 2.1 is to derive a priori exponential stability estimate for the transformed SRVRT problem (1.9). To this purpose, let \((u,\eta)\) be a solution of the transformed SRVRT problem and satisfy
where the initial data of \((u,\eta)\) enjoys assumptions (1)–(4) in Theorem 2.1, and δ is sufficiently small. We mention that the smallness condition (3.1) depends on Ω and other physical parameters in the transformed SRVRT problem, and will be repeatedly used throughout the rest of the article. Moreover, we assume that the solution \((u,\eta)\) possesses proper regularity, so that the procedure of formal derivation makes sense.
In order to exploit the regularity theory of the (steady) Stokes problem in the derivation of a priori estimates, we shall write (1.9)2–(1.9)5 as the following nonhomogeneous form, in which the terms on the left-hand side of the equations are linear:
where we have defined that
and \(\mathbb {D}_{\tilde {\mathcal {A}}}(u)\) and \(\operatorname {div}_{\tilde {\mathcal {A}}}\) are defined by (1.11) and (1.15) with \(\tilde {\mathcal {A}}\) in place of \(\mathcal {A}\), respectively. Since \(\det(\nabla\xi_{0})=1\), we have \(\det(\nabla\xi)=1\), i.e., \(\det(\nabla\eta+I)=1\).
This section is devoted to the derivation of preliminary estimates for \((\eta,u)\). To begin with, we shall recall some important inequalities, these inequalities will be frequently used in the rest of the article.
-
(1)
Sobolev’s embedding inequalities [1, Theorem 4.12]:
$$\begin{aligned}& \Vert f \Vert _{L^{p}}\lesssim \Vert f \Vert _{1}\quad\text{for } 2\leq p\leq6, \end{aligned}$$(3.6)$$\begin{aligned}& \Vert f \Vert _{C^{0}(\bar{\Omega})}\lesssim \Vert f \Vert _{2}. \end{aligned}$$(3.7) -
(2)
Korn’s inequality [10, Lemma 10.7]:
$$ \Vert w \Vert _{1}\lesssim \bigl\Vert \mathbb {D}(w) \bigr\Vert _{0}\quad\text{for any } w\in H_{0}^{1}. $$(3.8) -
(3)
Interpolation inequality \(H^{j}\) ([1, Theorem 5.2]):
$$ \Vert f \Vert _{j} \leq \Vert f \Vert _{0}^{1-\frac{j}{i}} \Vert f \Vert _{i}^{\frac{j}{i}} \leq C_{\varepsilon} \Vert f \Vert _{0}+\varepsilon \Vert f \Vert _{i} \quad\text{for any }0\leq j< i, \varepsilon>0, $$(3.9)where the constant \(C_{\varepsilon}\) depends on the domain and ε.
-
(4)
Estimates of the product of functions in Sobolev spaces [26]:
$$\begin{aligned}& \Vert f\psi \Vert _{j}\lesssim \left \{ \textstyle\begin{array}{l@{\quad}l} \Vert f \Vert _{1} \Vert \psi \Vert _{1}&\text{for }j=0,\\ \Vert f \Vert _{j} \Vert \psi \Vert _{2}&\text{for }0\leq j\leq2,\\ \Vert f \Vert _{2} \Vert \psi \Vert _{3}+ \Vert f \Vert _{3} \Vert \psi \Vert _{2} &\text{for }j=3, \end{array}\displaystyle \right . \end{aligned}$$(3.10)$$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{\frac{3}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{H^{\frac{3}{2}}(\mathbb {T})} \Vert \varphi \Vert _{H^{\frac{3}{2}}(\mathbb {T})}, \end{aligned}$$(3.11)$$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{-\frac{1}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{L^{4}(\mathbb {T})} \Vert \varphi \Vert _{L^{4}(\mathbb {T})}, \end{aligned}$$(3.12)$$\begin{aligned}& \Vert \phi\varphi \Vert _{H^{\frac{1}{2}}(\mathbb {T})} \lesssim \Vert \phi \Vert _{W^{1,\gamma}(\mathbb {T})} \Vert \varphi \Vert _{H^{\frac{1}{2}}(\mathbb {T})} \quad \text{for any }\gamma>2. \end{aligned}$$(3.13) -
(5)
Trace theorems [1, Theorem 7.58]:
$$\begin{aligned}& \bigl\Vert f(x_{h},0) \bigr\Vert _{W^{k,4}(\mathbb {T})} \lesssim \Vert f \Vert _{k+1}\quad\mbox{for any integer } k\geq0, \end{aligned}$$(3.14)$$\begin{aligned}& \bigl\Vert f(x_{h},0) \bigr\Vert _{H^{k+\frac{1}{2}}(\mathbb {T})} \lesssim \Vert f \Vert _{k+1}\quad\mbox{for any } k\geq0, \end{aligned}$$(3.15)$$\begin{aligned}& \vert u_{3} \vert _{-\frac{1}{2}}\lesssim \Vert u \Vert _{0}+ \Vert \operatorname {div}u \Vert _{0}\quad\mbox{for any } u:=(u_{1},u_{2},u_{3})\in H_{0}^{1}, \end{aligned}$$(3.16)where (3.16) can be derived by integration by parts and the inverse trace theorem. We mention that (3.6)–(3.10) also hold for the bounded domain.
Now, we start the derivation of some preliminary estimates. First, we derive bounds for divη. Since
one can derive from (1.9)1 that
Then, using the determinant expansion theorem, we have
Consequently,
Making use of (3.17), (3.10), and (3.1), we have
Second, we estimate for \(\mathcal {A}\) and \(\tilde {\mathcal {A}}\). Using (3.10) and (1.17), we have
Similarly, we can deduce from (1.9)1 that
Since δ is sufficiently small, we have the following relation:
which yields that
Using (3.22), (3.19), and (3.10), we can estimate that
In addition, exploiting (3.23), (3.19), and (3.8), we can easily deduce that, for any \(w\in H_{0}^{1}\),
which yield that, for sufficiently small δ,
Finally, we estimate the nonlinear terms \(\mathcal {N}\) and \(\mathcal {M}\). Recalling the definition of \(\mathcal {N}\), we use (3.23), (3.19), and (3.10) to infer that
Following the argument of (3.27), one has
Since we have the following relation
making use of (3.29), (3.10), and (3.7), we find that, for sufficiently small δ,
Exploiting (3.30), (3.23), (3.19), and (3.10), one estimates that
Consequently, exploiting the estimates (3.31), (3.23), (3.19), (3.15), (3.11), and (3.10), one has
Similarly, we can derive from (3.14) and (3.13) that
4 Estimates of η and u
In this section, we aim to deduce some estimates of η and u.
4.1 Estimates of η
This subsection is devoted to the derivation of the \(y_{h}\)-derivative estimates of η, the \(H^{3}\)-norm estimate of η, and some positive definiteness estimate under the stability condition.
Lemma 4.1
We have, for \(0\leq i\leq2\),
Proof
Applying \(\partial_{h}^{i}\) to (3.2), we have
Multiplying (4.2)1 by \(\partial_{h}^{i}\eta\) in \(L^{2}\), one obtains
Next, we estimate for \(I_{1}\)–\(I_{4}\).
Using the integration by parts, the boundary conditions in (4.2)4, and the second jump condition in (4.2)3, we have
where
Therefore, putting (4.4) into (4.3) and using Hölder’s inequality, we have
Exploiting the formula of integration by parts, (3.32), and (3.27), one obtains
and
Using Hölder’s inequality and (3.18), we can get that
Next we turn to estimate for \(I_{6}\) with \(i=0\). We can deduce from (3.17) that
which yields that
where we have defined that
Using the integration by parts, (3.15), and (3.10), we obtain that
Finally, inserting (4.8)–(4.10) and (4.13) into (4.7), we immediately deduce (4.1). □
In order to estimate η in \(H^{3}\)-norm, problem (3.2) shall be rewritten as the following two one-phase steady Stokes problems:
where
and \((w_{\pm},w_{\pm}|_{\Sigma})\) enjoys the following relation:
Lemma 4.2
We have
Proof
Applying the classical regularity of one-phase Stokes problem in [35] to (4.14), one has
which yields that
where we have defined that \(w=w_{+}\chi_{\Omega_{+}}+w_{-}\chi_{\Omega _{-}}\), \(\mathcal {G}=\mathcal {G}_{+}\chi_{\Omega_{+}}+\mathcal {G}_{-}\chi_{\Omega_{-}}\), and \(\mathcal {H}=\mathcal {H}_{+}\chi_{\Omega_{+}}+\mathcal {H}_{-}\chi_{\Omega_{-}}\).
Since
inserting the above equation into (4.20) yields
Making use of (3.27), (3.23), (3.18), (3.15), and (3.7), we have
and
Putting (4.24)–(4.26) into (4.23) yields (4.19). □
In order to control the negative terms containing g and η, we will establish the following positive definiteness estimate.
Lemma 4.3
We have
Proof
It is obvious that (4.27) holds with any \(\varphi\in H_{\sigma}^{1}\) in place of \(\partial_{h}^{i}\eta\). In fact, recalling the definition of \(\mathrm{C}_{\mathrm{r}}\) in (2.6), we have
which implies that
Therefore, together with \(\mathrm{C}_{\mathrm{r}}<1\) and Korn’s inequality (3.8), it implies that
To further deduce (4.27) from (4.29), we shall introduce Bogovskii’s function with the standing-wave form. We have the following conclusion:
Let \(\Omega'\) be a bounded Lipschitz domain. For any given \(f\in L^{2}(\Omega')\) satisfying \(\int_{\Omega'}f\,\mathrm {d}y=0\), there exists a Bogovskii’s function \(\tilde{\mathcal {B}}\in H_{0}^{1}(\Omega')\) such that \(\operatorname {div}\tilde{\mathcal {B}}[f]=f\) and
where the constant c only depends on the domain \(\Omega'\) (see [6], Theorem 10.11 or [7], Lemma III.3.1).
The above Bogovskii’s function defined on a bounded domain can be extended to the horizontal periodic domain Ω. In fact, we define that
Then \(\mathbb{C}\) is a bounded Lipschitz domain. We can use Bogovskii’s function defined on \(\mathbb {C}\) and an approach of horizontally translational extension to infer that, for any given \(g\in L^{2}\) satisfying \(\int_{\mathbb {C}} g \,\mathrm {d}y=0\), there exists a horizontally periodic Bogovskii’s function \(\mathcal {B}[g]\in H_{0}^{1}\) such that
for any integers \(k_{1}\) and \(k_{2}\). We call \(\mathcal {B}[g]\) Bogovskii’s function in a standing-wave form due to property (4.34).
Since \(\operatorname {div}\partial_{h}^{i}\eta\in L^{2}\) and \(\int_{\Omega} \operatorname {div}\partial_{h}^{i}\eta \,\mathrm {d}y=0\), then we can apply Bogovskii’s function to divη. Thus, using (4.30) and (3.18), we can infer that
Obviously, \(-\tilde{E}(\partial_{h}^{i}\eta)\) can be rewritten as follows:
Since \(\partial_{h}^{i}\eta-\mathcal {B}[\operatorname {div}\partial_{h}^{i}\eta]\in H_{\sigma}^{1}\), thus, using (4.29) and the Cauchy–Schwarz inequality, we obtain
In addition, we use (4.35), (3.15), and (3.1) to estimate that
Thanks to (4.37) and (4.38), we deduce from (4.36) that
which, together with Korn’s inequality (3.8), yields (4.27). □
4.2 Estimates of u
In this subsection, we deduce the \(y_{h}\)-derivative estimate of u, the temporal derivative estimates, and the elliptic estimates for \((u,q)\) in sequence.
Lemma 4.4
We have
Proof
The derivation of Lemma 4.4 is very similar to the one of Lemma 4.1. Multiplying (4.2) by \(\partial_{h}^{i}u\), and integrating the resulting identity over Ω, we have
Noting that
following the argument of (4.7), we have
where we have defined that
Following the argument of (4.8) and (4.9), we have
By (3.2)2, one further gets
Finally, we put the result (4.44) and (4.45) into (4.41), and get (4.39). This completes the proof of Lemma 4.4. □
Lemma 4.5
We have
Proof
Since , one has
Recalling the definition of n in (1.11) and the second jump condition in (1.9)4, we get
Hence, multiplying (1.9)2 by u in \(L^{2}\) and using (1.19), the jump condition (4.48), and the relation
we have
It is easy to estimate that
Inserting the above estimate into (4.49) yields that
Next we turn to estimate \(u_{t}\). Differentiating (1.9)2–(1.9)4 and the jump condition (4.48), we use (1.20) to deduce that
where we have defined that
Multiplying (4.52)1 by \(u_{t}\) in \(L^{2}\) and exploiting (4.52)2–(4.52)4, we have
We can estimate the integrals \(K_{3}\)–\(K_{6}\) as follows:
By (4.47), one has
In order to estimate \(K_{2}\), we use partial integrations and get
where we have defined that
Exploiting (3.21) for \(\mathcal {A}_{tt}\), we have
Since
one can exploit (3.14) and (3.12) to derive that
Exploiting (4.55)–(4.62), we can derive from (4.54) that
Finally, adding (4.63) to (4.51) and exploiting (3.26), we get (4.46). □
Next, we use the stratified steady Stokes regularity theory to estimate \((u,q)\). Problem (3.2) can be rewritten as the following standard form of the stratified steady Stokes problem:
where
Next, we obtain the following regularity result for problem (4.64).
Lemma 4.6
Let δ be sufficiently small, we have
Proof
Applying the classical regularity of stratified Stokes problem in [37, Theorem 3.1] to (4.64), we obtain that, for \(k=2\) and \(k=3\),
where we have exploited (3.23), (3.10), and (3.15) to estimate the second inequality in (4.67).
Since
then, making use of (4.68), (3.33), and (3.28), for sufficiently small δ, we derive from (4.67) with \(k=2\) that
which immediately implies (4.65).
Similarly, exploiting the estimates (3.32) and (3.27), for sufficiently small δ, we also get from (4.67) with \(k=3\) that
which implies (4.66). □
Next we establish an estimate for \(u_{t}(0)\).
Lemma 4.7
Let δ be sufficiently small, we have
Proof
We denote \(w:=\mathcal {A}^{T} u\) as in [2], then
Now, multiplying (3.2)1 by \(w_{t}\) in \(L^{2}\) and exploiting condition (4.72), we get
Exploiting (4.73), (3.33), (3.28), and (3.16), we have
Therefore, making use of (4.75), (4.77), (4.65), the smallness condition (3.1), and Young’s inequality, we deduce that
which yields (4.71). Furthermore, by (4.65) and (3.1), we deduce that
where \(c_{e}\) depends on the domain and other known physical parameters. □
5 Exponential stability
We are in the position to deduce (2.7). By Lemmas 4.1–4.5, (3.26), (4.27), and Young’s inequality, there exist positive constants \(c_{1}\)–\(c_{4}\) such that
Thus, we can derive from the above four inequalities (5.2)–(5.5) that
where we have defined that
and
By (4.66) and (4.27), there exist constants \(\tilde{c}_{5}\)–\(\tilde{c}_{7}\) and \(c_{8}\) such that
for any \(c_{5}>\tilde{c}_{5}\), \(c_{6}>\tilde{c}_{6}\), and \(c_{7}>\tilde{c}_{7}\). Thus, by (4.79), for any \(\delta\leq c_{8}/2c_{e}c_{2}(1+c_{5}+c_{6}+c_{7})\), we have
Noting that
we utilize (4.65), (4.29), (4.27), (3.8), and the Cauchy–Schwarz inequality to see that there exist sufficiently large \(c_{6}\) and sufficiently small \(c_{7}\) such that
for any sufficiently small δ. Obviously, \(\tilde{\mathcal {E}}\lesssim \mathcal {D}\). Thus, by (5.9), we can deduce that
from which, together with (5.10), we have
where we have defined that
On the other hand, by (4.71) we obtain
which, together with (5.11), yields
Consequently, we get Theorem 2.1 from the above a priori stability estimate (5.12) and the following local well-posedness of the transformed SRVRT problem.
Proposition 5.1
Let \((u_{0},\eta_{0})\) satisfy assumptions (1)–(4) in Theorem 2.1 and δ be sufficiently small, then the transformed SRVRT problem (1.9) possesses a unique global strong solution \((u,\eta)\in C^{0}([0,T),H^{2}\times H^{3})\) with an associated perturbation pressure q for some \(T>0\). Moreover, \((u,\eta,q)\) enjoys the following estimate:
Proof
Xu et al. [39] have established the local and global well-posedness results of the one-layer viscoelastic fluid model with upper free boundary. Exploiting the regularity theory for the stratified viscous flows in [38], we can easily extend the well-posedness results in [39] to the transformed SRVRT problem by a standard iteration method, and thus obtain Proposition 5.1. □
6 Conclusion
We investigate the stability of RT problem of the stratified incompressible viscoelastic fluids under the rotation and the gravity in a horizontal periodic domain, in which the rotation axis is parallel to the direction of gravity, the two fluids are immiscible, and the heavier fluid lies on the lighter one. We establish a stability condition for the RT problem. Moreover, we prove that, under the stability condition, the RT problem enjoys a unique solution which exponentially decays with respect to time. In addition, we note that the stability condition is independent of rotation angular velocity and the rotation has no destabilizing effect. However, we can observe that the rotation has no stabilizing effect from the experiment of Baldwin et al. Hence we will try to prove mathematically the stabilizing effect of the rotation in the future.
References
Adams, R.A., John, J.: Sobolev Space. Academic Press, New York (2005)
Beale, J.T.: Large-time regularity of viscous surface waves. Arch. Ration. Mech. Anal. 84, 307–352 (1984)
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability. The International Series of Monographs on Physics. Clarendon Press, Oxford (1961)
Duan, R., Jiang, F.: On the Rayleigh–Taylor instability for incompressible, inviscid magnetohydrodynamic flows. SIAM J. Appl. Math. 71, 1990–2013 (2012)
Duan, R., Jiang, F., Yin, J.P.: Rayleigh–Taylor instability for compressible rotating flows. Acta Math. Sci. Engl. Ser. 35, 1359–1385 (2015)
Feireisl, E., Novotny, A.: Singular Limits in Thermodynamics of Viscous Fluids. Birkhäuser, Basel (2009)
Galdi, G.P.: On the Rayleigh–Taylor instability for incompressible, inviscid magnetohydrodynamic flows (2001)
Guo, Y., Tice, I.: Compressible, inviscid Rayleigh–Taylor instability. Indiana Univ. Math. J. 60, 677–712 (2011)
Guo, Y., Tice, I.: Linear Rayleigh–Taylor instability for viscous, compressible fluids. SIAM J. Math. Anal. 42, 1688–1720 (2011)
Guo, Y., Tice, I.: Almost exponential decay of periodic viscous surface waves without surface tension. Arch. Ration. Mech. Anal. 207, 459–531 (2013)
Hu, X.P., Wang, D.H.: Local strong solution to the compressible viscoelastic flow with large data. J. Differ. Equ. 249, 1179–1198 (2010)
Hu, X.P., Wang, D.H.: Global existence for the multi-dimensional compressible viscoelastic flows. J. Differ. Equ. 250, 1200–1231 (2011)
Hu, X.P., Wang, D.H.: Strong solutions to the three-dimensional compressible viscoelastic fluids. J. Differ. Equ. 252, 4027–4067 (2012)
Hu, X.P., Wang, D.H.: Global existence and optimal decay rates for three-dimensional compressible viscoelastic flows. SIAM J. Math. Anal. 45, 2815–2833 (2013)
Hu, X.P., Wang, D.H.: The initial-boundary value problem for the compressible viscoelastic flows. Discrete Contin. Dyn. Syst. 35, 917–934 (2015)
Huang, G.J., Jiang, F., Wang, W.W.: On the nonlinear Rayleigh–Taylor instability of nonhomogeneous incompressible viscoelastic fluids under \(L^{2}\)-norm. J. Math. Anal. Appl. 455, 873–904 (2017)
Jiang, F.: An improved result on Rayleigh–Taylor instability of nonhomogeneous incompressible viscous flows. Commun. Math. Sci. 14, 1269–1281 (2016)
Jiang, F.: On effects of viscosity and magnetic fields on the largest growth rate of linear Rayleigh–Taylor instability. J. Math. Phys. 57, Article ID 111503 (2016)
Jiang, F., Jiang, S.: On instability and stability of three-dimensional gravity flows in a bounded domain. Adv. Math. 264, 831–863 (2014)
Jiang, F., Jiang, S., Wang, W.W.: On the Rayleigh–Taylor instability for two uniform viscous incompressible flows. Chin. Ann. Math., Ser. B 35, 907–940 (2014)
Jiang, F., Jiang, S.: On linear instability and stability of the Rayleigh–Taylor problem in magnetohydrodynamics. J. Math. Fluid Mech. 17, 639–668 (2015)
Jiang, F., Jiang, S.: On the stabilizing effect of the magnetic field in the magnetic Rayleigh–Taylor problem. SIAM J. Math. Anal. 50, 491–540 (2018)
Jiang, F., Jiang, S., Ni, G.X.: Nonlinear instability for nonhomogeneous incompressible viscous fluids. Sci. China Math. 56, 665–686 (2013)
Jiang, F., Jiang, S., Wang, W.W.: Nonlinear Rayleigh–Taylor instability in nonhomogeneous incompressible viscous magnetohydrodynamic fluids. Discrete Contin. Dyn. Syst., Ser. S 9, 1853–1898 (2016)
Jiang, F., Jiang, S., Wang, Y.J.: On the Rayleigh–Taylor instability for the incompressible viscous magnetohydrodynamic equations. Commun. Partial Differ. Equ. 39, 399–438 (2014)
Jiang, F., Jiang, S., Wu, G.C.: On stabilizing effect of elasticity in the Rayleigh–Taylor problem of stratified viscoelastic fluids. J. Funct. Anal. 272, 3763–3824 (2017)
Jiang, F., Wu, G.C., Zhong, X.: On exponential stability of gravity driven viscoelastic flows. J. Differ. Equ. 260, 7498–7534 (2016)
Lei, Z., Liu, C., Zhou, Y.: Global solutions for incompressible viscoelastic fluids. Arch. Ration. Mech. Anal. 188, 371–398 (2008)
Lin, F.H.: Some analytical issues for elastic complex fluids. Commun. Pure Appl. Math. 65, 893–919 (2012)
Lin, F.H., Liu, C., Zhang, P.: On hydrodynamics of viscoelastic fluids. Commun. Pure Appl. Math. LVIII, 1437–1471 (2005)
Lin, F.H., Zhang, P.: On the initial-boundary value problem of the incompressible viscoelastic fluid system. Commun. Pure Appl. Math. LXI, Article ID 0539 (2008)
Majda, A.J., Bertozzi, A.L.: Vorticity and Incompressible Flow. Cambridge University Press, Cambridge (2002)
Rayleigh, L.: Investigation of the character of the equilibrium of an in compressible heavy fluid of variable density. Sci. Pap. II, 200–207 (1990)
Taylor, G.I.: The stability of liquid surface when accelerated in a direction perpendicular to their planes. Proc. R. Soc. A 201, 192–196 (1950)
Temam, R.: Navier–Stokes Equations: Theory and Numerical Analysis. AMS Chelsea Publishing, New York (2001)
Wang, J.: Two-Dimensional Nonsteady Flows and Shock Waves. Science Press, Beijing (1994) (in Chinese)
Wang, Y.J., Tice, I.: The viscous surface-internal wave problem: nonlinear Rayleigh–Taylor instability. Commun. Partial Differ. Equ. 37, 1967–2028 (2012)
Wang, Y.J., Tice, I., Kim, C.: The viscous surface-internal wave problem: global well-posedness and decay. Arch. Ration. Mech. Anal. 212, 1–92 (2014)
Xu, L., Zhang, P., Zhang, Z.F.: Global solvability of a free boundary three-dimensional incompressible viscoelastic fluid system with surface tension. Arch. Ration. Mech. Anal. 208, 753–803 (2013)
Acknowledgements
The authors would like to thank the anonymous referee for invaluable suggestions, which improved the presentation of this paper. The authors also would like to thank BVOP for kindly considering their paper to be published.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Funding
The research of Xianjuan Li was partially supported by NSF of China (11771083, 61672005), and NSF of Fujian Province (2016J01013).
Author information
Authors and Affiliations
Contributions
All authors have made the same contribution and finalized the current version of this article. They read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jiang, Y., Li, X. & Zhao, Y. On the stability of Rayleigh–Taylor problem for stratified rotating viscoelastic fluids. Bound Value Probl 2018, 122 (2018). https://doi.org/10.1186/s13661-018-1041-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-1041-8