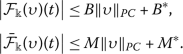- Research
- Open access
- Published:
Mathematical analysis of nonlinear integral boundary value problem of proportional delay implicit fractional differential equations with impulsive conditions
Boundary Value Problems volume 2021, Article number: 7 (2021)
Abstract
The current study is devoted to deriving some results about existence and stability analysis for a nonlinear problem of implicit fractional differential equations (FODEs) with impulsive and integral boundary conditions. The concerned problem involves proportional type delay term. By using Schaefer’s fixed point theorem and Banach’s contraction principle, the required conditions are developed. Also, different kinds of Ulam stability results are derived by using nonlinear analysis. Providing a pertinent example, we demonstrate our main results.
1 Introduction
In many real world problems, the fractional order models are found to be more suitable than integer order ones. More specifically, we can find the applications of fractional order derivatives and integrals in electrodynamics of complex medium, aerodynamics, polymer rheology, physics, chemistry, and so forth. For basic study and applications, we recommend the books and papers provided in [1–10]. Due to these applications, fractional order derivatives and integrals are gaining much importance and consideration from researchers nowadays. We refer to some recent work [11–18].
Problems with integral boundary conditions naturally arise in applied fields of science like thermal conduction problems, semiconductor problems, chemical engineering, blood flow problems, underground water flow problems, hydrodynamic problems, population dynamics, and so forth. For detailed study of integral boundary value problems, we recommend the papers [19–22].
Similarly, the dynamical systems with impulsive phenomena have been an object of great interest in many subjects such as physics, biology, economics, and engineering. The differential equations with impulsive conditions are used to model certain processes with discontinuous jumps and abrupt changes. Such processes cannot be modeled with classical differential equations (see [23–26]).
On the other hand, stability analysis has got greater interest in the last few years for FODEs. Because during numerical and optimal analysis such tools are greatly needed, see for instance [27]. Recently, for FODEs, the Ulam stability results have been considered very well. This concept of stability was introduced for the first time by Ulam and Hyers [28, 29] during 1941. It is nowadays known as Hyers–Ulam stability. This approach has stimulated a number of people to investigate stability of various mathematical problems. So, a large number of papers on Hyers–Ulam stability have been reported in the literature (see [30–34]). Motivated by the applications of impulsive and integral boundary value problems, in this paper we study the following nonlinear problem of implicit FODEs with impulsive and integral boundary conditions:

where \({}_{0}^{C}D_{t}^{\varsigma }\) represents the Caputo derivative, \(\mathrm{g}:[0, 1]\times \mathbb {R}^{3}\rightarrow \mathbb {R}\) and  are continuous functions, \(p>0\), \(q\geq 0\) are real numbers. Moreover,
are continuous functions, \(p>0\), \(q\geq 0\) are real numbers. Moreover,  ;
;  ,
,  are the right- and left-hand limits, respectively, at
are the right- and left-hand limits, respectively, at  for
for  .
.
Our considered problem (1) involves proportional delay term which includes a famous class of differential equations called pantograph. The pantograph differential equations form an important class of differential equations which has a wide range of applications in various applied fields of science, engineering and in economics. In economics the sudden rise and fall in stock exchange or in its status at time t as a function of that time with some delay which is inevitable in decision making problems is a practical significance of impulsive delay differential equations. Further, second order boundary value problems can be used to describe a large number of physical, mechanical, biological, and chemical phenomena. For some physical significance, we refer to some valuable work in [35–38].
2 Preliminaries
The space \(\mathscr{W}=C([0, 1],\mathbb {R})=\{\upsilon (t):\upsilon \in C([0, 1]) \}\) is a Banach space with respect to the norm defined by
Definition 2.1
([1])
The noninteger order integral of a function \(\mathrm{g}\in L^{1}([a,b],\mathbb {R}^{+})\) of order \(\varsigma \in \mathbb {R}^{+}\) is defined by
where Γ is the gamma function.
Definition 2.2
([1])
For a function g given on the interval \([a,b]\), the Caputo fractional order derivative of υ is defined by
where \(\ell =[\varsigma ]+1\).
Lemma 2.3
([39])
For \(\varsigma >0\), the given result holds:
We construct the following three inequalities for studying Hyers–Ulam stability of problem (1). Let \(x\in C([0, 1], \mathbb {R}_{+})\) be a nondecreasing function, \(\xi \geq 0\), \(\psi \in \mathscr{W}\), such that for  ,
,  , the following sets of inequalities are satisfied:
, the following sets of inequalities are satisfied:



where ς and m are the same as defined in problem (1).
Definition 2.4
([40])
If for \(\epsilon >0\) there exists a constant \(C_{\mathrm{g}}>0\) such that, for any solution \(\psi \in \mathscr{W}\) of inequality (5), there is a unique solution \(\upsilon \in \mathscr{W}\) of system (1) that satisfies
then problem (1) is Hyers–Ulam stable.
Definition 2.5
If for \(\epsilon >0\) and a set of positive real numbers \(\mathbb {R}^{+}\) there exists \(x\in C(\mathbb {R}^{+},\mathbb {R}^{+})\) with \(x(0)=0\) such that, for any solution \(\psi \in \mathscr{W}\) of inequality (6), there exist \(\epsilon >0\) and a unique solution \(\upsilon \in \mathscr{W}\) of problem (1) that satisfies
then problem (1) is generalized Hyers–Ulam stable.
Definition 2.6
([40])
If for \(\epsilon >0\) there exists a real number \(C_{\mathrm{g}}>0\) such that, for any solution \(\psi \in \mathscr{W}\) of inequality (7), there is a unique solution \(\upsilon \in \mathscr{W}\) of problem (1) that satisfies
then problem (1) is Hyers–Ulam–Rassias stable with respect to \((\xi ,x)\).
Definition 2.7
([40])
If there exists a constant \(C_{\mathrm{g}}>0\) such that, for any solution \(\psi \in \mathscr{W}\) of inequality (6), there is a unique solution \(\upsilon \in \mathscr{W}\) of problem (1) that satisfies
then problem (1) is generalized Hyers–Ulam–Rassias stable with respect to \((\xi ,x)\).
Remark 1
The function \(\psi \in \mathscr{W}\) is a solution of inequality (5) if there exist a function \(y\in \mathscr{W}\) and a sequence  ,
,  , which depends on ψ such that
, which depends on ψ such that
-
(i)
\(|y(t)|\leq \epsilon \),
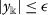 , \(t\in I\),
, \(t\in I\), -
(ii)
\({}_{0}^{C}D_{t}^{\varsigma }\psi (t)=\mathrm{g}(t, \psi (t), \psi (mt), {}_{0}^{C}D_{t}^{\varsigma }{\psi (t)})+y(t)\),
-
(iii)
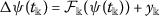 ,
, -
(iv)
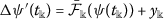 .
.
Remark 2
The function \(\psi \in \mathscr{W}\) is a solution of inequality (6) if there exist a function \(y\in \mathscr{W}\) and a sequence  ,
,  , which depends on ψ such that
, which depends on ψ such that
-
(i)
\(|y(t)|\leq x(t)\),
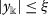 , \(t\in I\),
, \(t\in I\), -
(ii)
\({}_{0}^{C}D_{t}^{\varsigma }\psi (t)=\mathrm{g}(t, \psi (t), \psi (mt), {}_{0}^{C}D_{t}^{\varsigma }{\psi (t)})+y(t)\),
-
(iii)
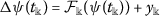 ,
, -
(iv)
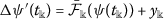 .
.
Remark 3
The function \(\psi \in \mathscr{W}\) is a solution of inequality (6) if there exist a function \(y\in \mathscr{W}\) and a sequence  ,
,  , which depends on ψ such that
, which depends on ψ such that
-
(i)
\(|y(t)|\leq \epsilon x(t)\),
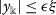 , \(t\in I\),
, \(t\in I\), -
(ii)
\({}_{0}^{C}D_{t}^{\varsigma }\psi (t)=\mathrm{g}(t, \psi (t), \psi (mt), {}_{0}^{C}D_{t}^{\varsigma }{\psi (t)})+y(t)\),
-
(iii)
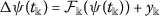 ,
, -
(iv)
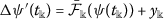 .
.
We give the proof of the following lemma, which provides a base for obtaining a solution to problem (1).
Lemma 2.8
Let \(\varsigma \in (1, 2]\), \(\alpha :[0, 1]\rightarrow \mathbb {R}\) be a continuous function, then the function \(\upsilon \in \mathscr{W}\) is the solution to the following problem:

if and only if υ satisfies the following integral equation:

where

Proof
Assume that, for \(t\in [0, t_{1}]\), υ is a solution of (8). Then, by Lemma 2.3, there exist \(a_{1},a_{2}\in \mathbb {R}\) such that
which also yields
Let, for \(t\in (t_{1}, t_{2}]\), us have \(d_{1},d_{2}\in \mathbb {R}\) with
This leads us to
Corresponding to impulsive conditions, we have
one has
Thus (12) implies
Similarly, for  , one has
, one has

which by differentiation gives the result

Using the given boundary conditions in (10), (11), we obtain
and

Thus, in view of \(p\upsilon (1)+q\upsilon '(1)=\int _{0}^{1}h_{2}(\upsilon (z))\,dz\) and the result (15), we get the following values for \(-a_{1}\) and \(-a_{2}\):

Putting these values for \(-a_{1}\) and \(-a_{2}\) in (10) and (13), we get (9). □
3 Main results
Corollary 3.1
As a result of Lemma 2.8, problem (1) has the following solution:

where

For the purpose of simplicity, we take \(\Phi _{\upsilon }(t)=\mathrm{g}(t, \upsilon (t), \upsilon (mt), {}_{0}^{C}D_{t}^{\varsigma }{\upsilon (t)})\). To transform problem (1) to a fixed point problem, here we define the operator \(\mathscr{Z}:\mathscr{W}\rightarrow \mathscr{W}\) by

The given assumptions are necessary for obtaining our main results.
- \((H_{1})\):
-
Let \(\mathrm{g}:[0, 1]\times \mathbb {R}\times \mathbb {R}\times \mathbb {R} \rightarrow [0,\infty )\) be a jointly continuous function;
- \((H_{2})\):
-
For every \(\upsilon , \bar{\upsilon }\in C([0, 1],\mathbb {R})\) and \(L_{\mathrm{g}}>0\), \(0< N_{\mathrm{g}}<1\), let the following inequality
$$\begin{aligned}& \bigl\vert \mathrm{g}\bigl(t, \upsilon (t), \upsilon (mt), \Phi _{\upsilon }(t)\bigr)- \mathrm{g}\bigl(t, \bar{\upsilon }(t), \bar{\upsilon }(mt), \Phi _{ \bar{\upsilon }}(t)\bigr) \bigr\vert \\& \quad \leq L_{\mathrm{g}}\bigl( \bigl\vert \upsilon (t)-\bar{\upsilon }(t) \bigr\vert + \bigl\vert \upsilon (mt)-\bar{\upsilon }(mt) \bigr\vert \bigr)+N_{\mathrm{g}}\bigl|\Phi _{\upsilon }(t)- \Phi _{\bar{\upsilon }}(t)\bigr| \end{aligned}$$hold;
- \((H_{3})\):
-
There exist \(C_{1}, C_{2}>0\) such that the following relations hold true:
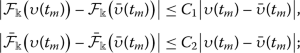
- \((H_{4})\):
-
There exist constants \(C_{3}\), \(C_{4}>0\) such that, for all \(\upsilon \in \mathbb {R}\), the following inequalities hold true:
$$\begin{aligned}& \bigl\vert h_{1}\bigl(\upsilon (t)\bigr)-h_{1}\bigl( \bar{\upsilon }(t)\bigr) \bigr\vert \leq C_{3} \bigl\vert \upsilon (t)- \bar{\upsilon }(t) \bigr\vert , \\& \bigl\vert h_{2}\bigl(\upsilon (t)\bigr)-h_{2}\bigl( \bar{\upsilon }(t)\bigr) \bigr\vert \leq C_{4} \bigl\vert \upsilon (t)- \bar{\upsilon }(t) \bigr\vert ; \end{aligned}$$ - \((H_{5})\):
-
There exist constants \(C_{5}\), \(C_{6}>0\) such that, for all \(\upsilon \in \mathbb {R}\),
$$\begin{aligned}& \bigl\vert h_{1}\bigl(\upsilon (t)\bigr) \bigr\vert \leq C_{5}, \\& \bigl\vert h_{2}\bigl(\upsilon (t)\bigr) \bigr\vert \leq C_{6}; \end{aligned}$$ - \((H_{6})\):
-
There exist functions \(\theta _{1}, \theta _{2}, \theta _{3} \in C([0, 1],\mathbb {R}^{+})\) with
$$\begin{aligned}& \bigl\vert \mathrm{g}\bigl(t, \upsilon (t), \upsilon (m t), {}_{0}^{C}D_{t_{\jmath }}^{\varsigma }\upsilon (t) \bigr) \bigr\vert \\& \quad \leq \theta _{1}(t)+\theta _{2}(t) \bigl( \vert \upsilon \vert + \bigl\vert \upsilon (m t) \bigr\vert \bigr)+ \theta _{3}(t) \bigl\vert {}_{0}^{C}D_{t_{\jmath }}^{\varsigma } \upsilon (t) \bigr\vert \quad \text{for } t \in [0, 1], \upsilon \in \mathscr{W}, \end{aligned}$$such that \(\theta _{3}^{*}=\max_{t\in I}|\theta _{3}(t)|<1\);
- \((H_{7})\):
-
If g,
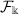 ,
,  are continuous functions and there exist constants B, \(B^{*}\), M, \(M^{*}>0\) such that, for all \(\upsilon \in \mathscr{W}\), the following inequalities are satisfied:
are continuous functions and there exist constants B, \(B^{*}\), M, \(M^{*}>0\) such that, for all \(\upsilon \in \mathscr{W}\), the following inequalities are satisfied:
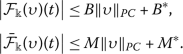
Theorem 3.2
If assumptions \((H_{1})\)–\((H_{6})\) are satisfied, then problem (1) has at least one solution.
Proof
To prove this result, here we apply Schaefer’s fixed point theorem.
Step 1: We will show that \(\mathscr{Z}\) is continuous. We take a sequence \(\upsilon _{n}\in \mathscr{W}\) with \(\upsilon _{n}\rightarrow \upsilon \in \mathscr{W}\). We consider

where \(\Phi _{\upsilon _{n}}(t), \Phi _{\upsilon }(t)\in \mathscr{W}\) satisfy the following functional equations:
By the application of assumption \((H_{2})\), we have
Then
Now we see as \(n\rightarrow \infty \), \(\upsilon _{n}\rightarrow \upsilon \), which implies that \(\Phi _{\upsilon ,n}\rightarrow \Phi _{\upsilon }\). Let there exist \(\mathbf{b}>0\) such that, for each t, \(|\Phi _{\upsilon ,n}(t)| \leq \mathbf{b}\) and \(|\Phi _{\upsilon }(t)|\leq \mathbf{b}\). Then
For each \(t\in [0, t]\), the functions \(z\rightarrow 2\mathbf{b}(t-z)^{\varsigma -1}\), \(z\rightarrow 2\mathbf{b}(t_{\jmath }-z)^{\varsigma -1}\), \(z\rightarrow 2\mathbf{b}(t_{\jmath }-z)^{\varsigma -2}\), \(z\rightarrow 2\mathbf{b}(1-z)^{\varsigma -1}\), \(z\rightarrow 2\mathbf{b}(1-z)^{\varsigma -2}\) are integrable. Hence, applying Lebesgue dominated convergent theorem, we have \(|\mathscr{Z}\psi _{n}(t)-\mathscr{Z}\psi (t)|\rightarrow 0\) as \(t\rightarrow \infty \). This implies \(\|\mathscr{Z}\psi _{n}-\mathscr{Z}\psi \|\rightarrow 0\) as \(t\rightarrow \infty \). Therefore, \(\mathscr{Z}\) is continuous.
Step 2: In this step we need to show that \(\mathscr{Z}\) is bounded. Consequently, for each \(\upsilon \in \mathscr{E}=\{\upsilon \in \mathscr{W} : \|\upsilon \|_{PC} \leq \mathbf{r}^{*}\}\), we have to show that \(\|\mathscr{Z}\upsilon \|_{\mathscr{W}}\leq \eta \), where η is a positive real number. Then, for  , we have
, we have

Apply assumption \((H_{6})\) to get
Taking maximum of both sides, we have
which further implies
where \(\theta _{1}^{*}=\max_{t\in I}|\theta _{1}(t)|\), \(\theta _{2}^{*}=\max_{t\in I}|\theta _{2}(t)|\), and \(\theta _{3}^{*}=\max_{t\in I}|\theta _{3}(t)|<1\).
Hence from (18) we get
This shows that \(\mathscr{Z}\) is bounded.
Step 3: \(\mathscr{Z}\) maps bounded sets into equicontinuous sets of \(\mathscr{W}\). Let  such that \(\tau _{1}<\tau _{2}\). And let \(\mathscr{E}\) be a bounded set of \(\mathscr{W}\) as in Step 2, let \(\upsilon \in \mathscr{E}\). Then
such that \(\tau _{1}<\tau _{2}\). And let \(\mathscr{E}\) be a bounded set of \(\mathscr{W}\) as in Step 2, let \(\upsilon \in \mathscr{E}\). Then

Taking into account the assumptions, we obtain

We see as \(\tau _{1}\) tends to \(\tau _{2}\), the right-hand side of (20) tends to 0. Thus by “Arzelà–Ascoli theorem” \(\mathscr{Z}\) is completely continuous.
Step 4: Here the set defined by \(\mathscr{E}_{\sigma }=\{\upsilon \in \mathscr{W} :\upsilon = \sigma \mathscr{Z}\upsilon \text{ for } 0<\sigma <1\}\) is bounded. Let \(\upsilon \in \mathscr{E}_{\varsigma }\). Then by definition \(\upsilon = \varsigma \mathscr{Z}\upsilon \). From Step 2, we get
which shows that \(\mathscr{E}_{\sigma }\) is bounded. Therefore, by Schaefer’s fixed point theorem, \(\mathscr{Z}\) has at least one fixed point and hence problem (1) has at least one solution. □
Theorem 3.3
If assumptions \((H_{1})\)–\((H_{4})\) and the inequality
are satisfied, then the problem has a unique solution in the interval \([0, 1]\).
Proof
Assume that \((H_{1})\)–\((H_{3})\) and inequality (21) are satisfied. Then, for \(\upsilon , \bar{\upsilon }\in \mathscr{W}\), we consider

where
By the application of assumption \((H_{2})\), we have
Then
Thus from (22) we get the following result in its simplified form:
where
Therefore, by the Banach contraction principle, operator \(\mathscr{Z}\) has a unique fixed point. □
4 Stability analysis of problem (1)
Here we derive results about “Hyers–Ulam and Hyers–Ulam–Rassias” stability for problem (1).
Theorem 4.1
If assumptions \((H_{1})\)–\((H_{4})\) and inequality (21) are satisfied, then problem (1) is Hyers–Ulam stable.
Proof
Let \(\psi \in \mathscr{W}\) be any solution of inequality (5) and υ be a unique solution of (1). Then, using Remark 1, for \(t\in [0,1]\),  (
( ), we have
), we have

By Corollary 3.1, the solution of (23) is given by

where

Then, for  , we have
, we have

Using assumptions \((H_{1})\)–\((H_{4})\) and (i) of Remark 1, we get the result
where
This implies that
We see that
Therefore, problem (1) is Hyers–Ulam stable. □
Corollary 4.2
In Theorem 4.1, if we set \(x(\epsilon )=C_{g}(\epsilon )\) such that \(x(0)=0\), then problem (1) becomes generalized Hyers–Ulam stable.
To prove the next result, we further need another assumption as follows:
- \((H_{8})\):
-
Let, for a nondecreasing function \(x \in {C(I, \mathbb {R})}\), there exist constants \(\mu _{x}>0\), \(\epsilon >0\) such that
$$ {{}_{0}I_{t}}^{\varsigma }x(t)\leq \mu _{x}x(t). $$
Theorem 4.3
If assumptions \((H_{1})\)–\((H_{4})\), \((H_{8})\) and inequality (21) are satisfied, then problem (1) is Hyers–Ulam–Rassias stable with respect to \((\xi , x)\).
Proof
Let \(\psi \in \mathscr{W}\) be any solution of inequality (6) and υ be a unique solution of problem (1). Then, from the above proof of Theorem 4.1, we obtain the following result for  :
:

Using assumptions \((H_{1})\)–\((H_{4})\), \((H_{8})\), and Remark 3, we get the result
Simplifying further, we have
where
Therefore, problem (1) is Hyers–Ulam–Rassias stable. □
5 Applications
Example 1

where e is an exponential function, \(p=q=1\).
Here
with \(\varsigma =\frac{3}{2}\), \(m=\frac{1}{4}\). The continuity of g is obvious.
By hypothesis \((H_{2})\), for any \(\upsilon , \bar{\upsilon } \in \mathbb {R}\), we have
Hence g satisfies hypothesis \((H_{2})\) with \(L_{\mathrm{g}}=N_{\mathrm{g}}=\frac{1}{38}\). Also hypothesis \((H_{4})\) holds with \(\theta _{0}(t)=\frac{e(-\pi t)}{15}\), \(\theta _{1}(t)=\theta _{2}(t)=\frac{e(-t)}{38+t}\), where \(\theta _{0}^{*}(t)=\frac{1}{15}\), \(\theta _{1}^{*}(t)=\theta _{2}^{*}(t)=\frac{1}{38}\).
At \(t_{1}=\frac{1}{3}\) the impulsive conditions are given as follows:
For any \(\upsilon , \bar{\upsilon }\in \mathrm{E}\), we have
which satisfy \((H_{3})\) with real constants \(C_{1}=\frac{1}{60}\), \(C_{2}=\frac{1}{80}\). And
satisfy \((H_{4})\) with real constants \(C_{3}=\frac{1}{16}\), \(C_{4}=\frac{1}{20}\). So we have
Therefore, by Theorem 3.3, problem (28) has a unique solution. And by result Theorem 4.1, problem (28) is Hyers–Ulam stable. Similarly, by setting \(x(t)=t\), taking \(\xi =1\), and applying the obtained result Theorem 4.3, it is obvious that, for any \(t\in [0,1]\), the numerical problem (28) is Hyers–Ulam–Rassias stable with respect to \((\xi ,x)\).
6 Conclusion
By using classical fixed point results, we have established some useful results about the existence and stability of Ulam type for an impulsive problem of FODEs under integral boundary conditions. The concerned results have been testified by an example. Hence fixed point approach is a powerful technique to investigate various nonlinear problems of impulsive FODEs which have many applications in dynamics and fluid mechanics.
Availability of data and materials
This is not applicable.
References
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Academic Press, San Diego (1998)
Lakshmikantham, V., Vatsala, A.S.: Basic theory of fractional differential equations. Nonlinear Anal., Theory Methods Appl. 69(8), 2677–2682 (2008)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Kilbas, A.A., Marichev, O.I., Samko, S.G.: Fractional Integrals and Derivatives. Gordon & Breach, Yverdon (1993)
Yang, X.J.: Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Therm. Sci. 21(3), 1161–1171 (2017)
Metzler, W., et al.: Relaxation in filled polymers: a fractional calculus approach. J. Chem. Phys. 103(16), 7180–7186 (1995)
Wang, G., Ren, X., et al.: Radial symmetry of standing waves for nonlinear fractional Laplacian Hardy–Schrödinger systems. Appl. Math. Lett. 96, 106560 (2020)
Zhang, L., Hou, W.: Standing waves of nonlinear fractional p-Laplacian Schrödinger equation involving logarithmic nonlinearity. Appl. Math. Lett. 102, 106149 (2020)
Wang, G., Ren, X., Bai, Z., Hou, W.: Radial symmetry of standing waves for nonlinear fractional Hardy–Schrödinger equation. Appl. Math. Lett. 96, 131–137 (2019)
Jarad, F., Harikrishnan, S., Shah, K., Kanagarajan, K.: Existence and stability results to a class of fractional random implicit differential equations involving a generalized Hilfer fractional derivative. Discrete Contin. Dyn. Syst., Ser. S 13(3), 723–739 (2020)
Wang, J., Shah, K., Ali, A.: Existence and Hyers–Ulam stability of fractional nonlinear impulsive switched coupled evolution equations. Math. Methods Appl. Sci. 41(6), 2392–2402 (2018)
Ullah, A., Shah, K., Abdeljawad, T., Khan, R.A., Mahariq, I.: Study of impulsive fractional differential equation under Robin boundary conditions by topological degree method. Bound. Value Probl. 2020(1), 98 (2020)
Ahmed, I., Kumam, P., Abdeljawad, T., Jarad, F., Borisut, P., Demba, M.A., Kumam, W.: Existence and uniqueness results for ϕ-Caputo implicit fractional pantograph differential equation with generalized anti-periodic boundary condition. Adv. Differ. Equ. 2020(1), 555 (2020)
Arnold, M., Simeon, B.: Pantograph and catenary dynamics: a benchmark problem and its numerical solution. Appl. Numer. Math. 34, 345–362 (2000)
Khan, H., Khan, A., Jarad, F., Shah, A.: Existence and data dependence theorems for solutions of an ABC-fractional order impulsive system. Chaos Solitons Fractals 131, 109477 (2020)
Feng, B.: On the blow-up solutions for the fractional nonlinear Schrödinger equation with combined power-type nonlinearities. Commun. Pure Appl. Anal. 17(5), 1785–1804 (2018)
Feng, B.: On the blow-up solutions for the nonlinear Schrödinger equation with combined power-type nonlinearities. J. Evol. Equ. 18(1), 203–220 (2018)
Song, W., Gao, W.: Positive solutions for a second-order system with integral boundary conditions. Electron. J. Differ. Equ. 2011, 13 (2011)
Ahmad, B., Nieto, J.J.: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Bound. Value Probl. 2009, Article ID 708576 (2009)
Ahmad, B., Alsaedi, A., Alghamdi, B.S.: Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions. Nonlinear Anal., Real World Appl. 9(4), 1727–1740 (2008)
Yang, Z.: Existence of nontrivial solutions for a nonlinear Sturm–Liouville problem with integral boundary conditions. Nonlinear Anal., Theory Methods Appl. 68(1), 216–225 (2008)
Asma, Ali, A., Shah, K., Jarad, F.: Ulam–Hyers stability analysis to a class of nonlinear implicit impulsive fractional differential equations with three point boundary conditions. Adv. Differ. Equ. 2019, 7 (2019)
Benchohra, M., Henderson, J., Ntouyas, S.: Impulsive Differential Equations and Inclusions, 1st edn. Contemporary Mathematics and Its Applications, vol. 2. Hindawi Publishing Corporation, New York (2006)
Abdo, M.S., Abdeljawad, T., Shah, K., Jarad, F.: Study of impulsive problems under Mittag-Leffler power law. Heliyon 6(10), e05109 (2020)
Lakshmikantham, V., Bainov, D.D., Semeonov, P.S.: Theory of Impulsive Differential Equations. Worlds Scientific, Singapore (1989)
Feng, B., Zhang, H.: Stability of standing waves for the fractional Schrödinger–Choquard equation. Comput. Math. Appl. 75(7), 2499–2507 (2018)
Ulam, S.M.: Problems in Modern Mathematics. Wiley, New York (1940)
Hyers, D.H.: On the stability of the linear functional equations. Proc. Natl. Acad. Sci. USA 27, 222–224 (1941)
Zada, A., Ali, W., Park, C.: Ulam’s type stability of higher order nonlinear delay differential equations via integral inequality of Grönwall–Bellman–Bihari’s type. Appl. Math. Comput. 350, 60–65 (2019)
Ali, A., Shah, K.: Existence theory and Ulam–Hyers stability to anti-periodic integral boundary value problem of implicit fractional differential equations. Appl. Math. E-Notes 19, 228–242 (2019)
Shah, K., Ali, A., Bushnaq, S.: Hyers–Ulam stability analysis to implicit Cauchy problem of fractional differential equations with impulsive conditions. Math. Methods Appl. Sci. 41, 1–15 (2018)
Ali, A., Shah, K., Baleanu, D.: Ulam stability results to a class of nonlinear implicit boundary value problems of impulsive fractional differential equations. Adv. Differ. Equ. 2019, 5 (2019)
Ali, A., Rabieib, F., Shah, K.: On Ulam’s type stability for a class of impulsive fractional differential equations with nonlinear integral boundary conditions. J. Nonlinear Sci. Appl. 10, 4760–4775 (2017)
Shi, Y.D., Zhou, Q.D., Li, Y.: A note on a two-point boundary value problem arising from a liquid metal flow. SIAM J. Math. Anal. 28(5), 1086–1093 (1997)
Horgan, C.O., Saccomandi, G., Sgura, I.: A two-point boundary-value problem for the axial shear of hardening isotropic incompressible nonlinearly elastic materials. SIAM J. Appl. Math. 62(5), 1712–1727 (2002)
Alexeyeva, L.A., Zakiryanova, G.K.: Singular boundary integral equations of boundary value problems for hyperbolic equations of mathematical physics. In: Mathematical Theorems. IntechOpen, London (2020)
Benchohra, M., Nieto, J., Ouahab, A.: Second-order boundary value problem with integral boundary conditions. Bound. Value Probl. 2011(1), Article ID 260309 (2011)
Cabada, A., Wang, G.: Positive solutions of nonlinear fractional differential equations with integral boundary value conditions. J. Math. Anal. Appl. 389(1), 403–411 (2013)
Rus, I.A.: Ulam stabilities of ordinary differential equations in a Banach space. Carpath. J. Math. 26, 103–107 (2010)
Acknowledgements
All the authors are thankful to the reviewers for their careful reading and suggestions.
Funding
There is no source of funding.
Author information
Authors and Affiliations
Contributions
All authors have equal contributions in this paper. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ali, A., Shah, K., Abdeljawad, T. et al. Mathematical analysis of nonlinear integral boundary value problem of proportional delay implicit fractional differential equations with impulsive conditions. Bound Value Probl 2021, 7 (2021). https://doi.org/10.1186/s13661-021-01484-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-021-01484-y
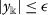 ,
, 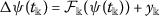 ,
,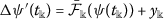 .
.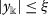 ,
, 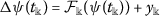 ,
,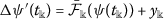 .
.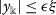 ,
, 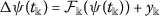 ,
,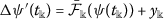 .
.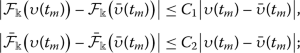
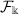 ,
,  are continuous functions and there exist constants B,
are continuous functions and there exist constants B,