- Research
- Open access
- Published:
Revisiting generalized Caputo derivatives in the context of two-point boundary value problems with the p-Laplacian operator at resonance
Boundary Value Problems volume 2023, Article number: 62 (2023)
Abstract
The novelty of this paper is that, based on Mawhin’s continuation theorem, we present some sufficient conditions that ensure that there is at least one solution to a particular kind of a boundary value problem with the p-Laplacian and generalized fractional Caputo derivative.
1 Introduction
Fractional calculus broadens the classical calculus by generalizing differentiation and integration of integer order and studies these operators with arbitrary order so that they take the fundamental operator \(\mathrm{D}^{\varrho }\) where \(\varrho \in \mathbb{C}\). There are numerous approaches to fractional derivatives, including Caputo, Weyl, Hadamard, Grünwald–Letnikov, Riemann–Liouville, and others (see, for instance, [1, 2]). The Caputo FD lends itself well to conceptual interpretations of initial and boundary conditions. Despite these challenges, researchers have proposed local fractional derivatives and integrals because of the complicated process and not possessing certain fundamental characteristics fulfilled by standard derivatives. The standard conformable derivative (shortly, \(\mathscr{CD}\)) was initiated by the authors of [3, 4]. F. Jarad et al. [5, 2017] recently presented a modified version of the fractional conformable integral operator.
The problem of turbulent flow in a porous medium is fundamental in mechanics. The p-Laplacian equation was first presented by L. S. Leibenson as a model for the aforementioned problem in [6, 1983]. A characteristic extension of the p-Laplacian differential equation was put forth by replacing the ordinary derivative with an FD, which produced the fractional p-Laplacian equation, therefore as direct consequence of the advancement of FD. Boundary value problems with integral and multipoint boundary conditions on an unbounded domain have many practical applications, including the study of physical phenomena like the unsteady flow of fluid through a semiinfinite porous medium and radially symmetric answers to nonlinear elliptic equations. They also appear in the study of drain flows and plasma physics (see [7–12]). This interest has led to the publication of several findings and the investigation of various forms of the p-Laplacian equation (see [13–16]).
Over the past few years, there has been a lot of research done on the boundary value problems (abbreviated BVPs) that are defined by fractional differential equations (shortly, FDE). Numerous papers have recently examined boundary value issues for \(\mathscr{FDE}\) at nonresonance (see [17–21]). Furthermore, the BVPs for differential equations at resonance have been investigated in a number of papers (see [22–24]). With the help of various fixed point theorems, including the fixed point theorems of Leggett–Williams, Schaefer, Krasnosel’skii, the topological degree of vector fields and maps, and the fixed point index, numerous fascinating findings relating to the existence, uniqueness, and stability results have been reported (see [25–29]). In order to analyze functional and differential equations, the concept of coincidence degree theory was first presented in 1977 by the authors of [30]. The hypothesis is known as Mahwin’s coincidence degree theory due to the significant outcome of Mawhin’s research and his significant contributions to the field of coincidence degree theory (shortly, \(\mathscr{CDE}\)) (see [30–33]). In particular, when there are nonlinear equations involved in the problem, coincidence theory is a very potent tool. It has numerous applications, but it is particularly useful in determining whether periodic solutions to nonlinear differential equations exist (see [34]).
Most of these interdisciplinary research fields have nonlinear problems that can be constructed mathematically in following way:
in which a Banach space is represented by \(\mathcal{Y}\) and a nonempty set represented by \(\mathcal{X}\), and \(\mathscr{L},\mathscr{N}\) are mappings from \(\mathcal{X}\) to \(\mathcal{Y}\). A coincidence problem is the problem of solving equation (1.1).
There has been a massive increase in the investigation of second-order nonlinear ordinary differential equations (shortly, \(\mathscr{ODE}\)) of the form
depending on the area of interest, various boundary conditions may apply (see [35]).
The p-Laplacian equation was explored in [6], which opened up new directions for future research:
where \(\psi_{\vartheta} ( \rho ) = \vert \rho \vert ^{\vartheta-2}\rho, \infty >\vartheta>1, \rho\in \mathbb{R}\). The nonlinear fractional boundary value problem was initiated by Bai and Lu [18], and examined the existence and abundance of positive solutions:
and boundary conditions
Following fractional boundary value problem was explored by the authors of [17]:
with the boundary conditions in (1.5), where \(\mathit{D}_{\theta}^{\alpha }\) and \(\mathit{D}_{ \theta}^{\varrho }\) are Riemann–Liouville fractional operators with \(0<\alpha <\varrho \leq 2\). With the aid of cone-based fixed point theorems, they proved the existence results. As we know, an improved outcome that proves the existence of (1.6) solution continua that meet the aforementioned requirements is also possible.
The boundary value problem (1.4)–(1.5) happens to be at resonance in the sense that its associated linear homogeneous BVP
and the conditions in (1.5) have \(x(\theta )=ct^{\varrho -1}\), \(c\in \mathbb{R}\) as a nontrivial solution when \(c\neq 0\).
In order to deal with fractional-BVP at resonance, the authors of [13] have taken into account a BVP with two-points considering p-Laplacian operator provided by
with the condition
Wang et al. [24], in their study of the two-point BVP for \(\mathscr{FDE}\) (1.8) at resonance with different boundary conditions
made use of the \(\mathscr{CDT}\) to obtain the results for existence.
The BVP for fractional order at resonance is only briefly discussed in a few papers, though. The existence of solutions pertaining to Sturm–Liouville and Dirichlet problems has become the topic of several works.
Motivated by the preceding results, by means of Mawhin’s continuation theorem, we present some sufficient conditions which guarantee the existence of at least one solution for a type of boundary value problem with p-Laplacian and in the framework of a specific type of generalized fractional Caputo derivative. More clearly, in this paper with the aid of \(\mathscr{CDT}\), we examine the existence of solutions for a two-point FDE at resonance
with the condition for (1.11) being
where \(( {}^{c}\mathcal{D}_{0+,\theta}^{\varrho,\gamma } ) \) and \(( {}^{c}\mathcal{D}_{0+,\mu }^{ \alpha,\gamma } ) \) denote generalized Caputo derivative with \(0<\alpha \leq \alpha +\varrho <1, 0<\gamma \), with \(\mathscr{A}\) continuous (but not necessarily locally Lipschitz continuous).
Note that the nonlinear operator \({}^{c}\mathcal{D}_{0+,\theta}^{\varrho,\gamma } [ \psi _{\vartheta} ( {}^{c} \mathcal{D}_{0+,\mu }^{\alpha, \gamma } ) ] \) is restricted to \(( {}^{c}\mathcal{D}_{0+,\theta}^{\varrho +\alpha,\gamma } ) \) if we take \(\vartheta=2\). Furthermore, the index law of additiveness,
holds when the function \(u ( \theta ) \) is subjected to some fair constraints (see [5, Theorem 4.6]).
Additionally, the \(\mathscr{CDT}\) for linear differential operators with boundary conditions cannot be directly applied to \({}^{c}\mathcal{D}_{0+}^{\varrho,\gamma } [ \psi _{ \vartheta} ( {}^{c}\mathcal{D}_{0+, \mu }^{\alpha,\gamma } ) ] \) because it is a nonlinear operator.
The problem (1.11)–(1.12) is transformed into a two-point BVP of second order \(\mathscr{ODE}\) in the special case of \(\vartheta=2\) and \(\alpha =\varrho =1\).
The remaining of this paper is organized as follows: The next section presents some preliminaries. In Sect. 3, by employing the Mawhin’s continuation theorem of coincidence degree theory, a criterion is established for the existence of solutions of BVP (1.11)–(1.12). Finally, an example is presented to illustrate our theoretical result. We claim that the results of this paper are new and generalize some earlier results.
2 Basic definitions and preliminaries
According to Khalil et al. [3], an intriguing concept that expands on the well-known limit definition of the derivative of a function is presented below.
Definition 2.1
([3])
The \(\mathscr{CD}\) and its order \(\varrho \in ( 0,1 ] \) is provided by
The properties of \(T_{0+}^{\varrho } [ u ] \) can be found in [3, 4].
Definition 2.2
([4])
Let us assume that ϱ \(\in ( \hbar,\hbar +1 ] \), u is an ħ-differentiable function at \(\theta >0\), thus, at \(\theta >0\), the left-sided \(\mathscr{CD}\) of order ϱ is given by
Lemma 2.3
([4])
Let us assume \(\theta >0\), ϱ \(\in ( \hbar,\hbar +1 ] \). Then u is \((\hbar +1)\)-differentiable iff u is ϱ-differentiable, furthermore, \(\mathbf{T}_{0+,\theta}^{\varrho } [ u ] =\theta ^{\hbar +1- \varrho }u^{ ( \hbar +1 ) } ( \theta ) \).
Remark 2.4
As a simple example, if ϱ \(\in ( \hbar,\hbar +1 ] \), we have \(\mathbf{T}_{0+,\theta}^{\varrho } [ \mu ^{k} ] =0\) whenever \(k=0,1,\dots,\hbar \).
Definition 2.5
([4])
Consider ϱ \(\in ( \hbar,\hbar +1 ] \). The left-sided conformable integral of order ϱ of a function \(u \in C ( ( 0,+\infty ), \mathbb{R} )\) is given by
when \(u^{ ( \hbar ) } ( \theta ) \) exists.
In order to obtain an equivalent integral representation of the BVP (1.11)–(1.12), the lemma below is crucial.
Lemma 2.6
([4])
Let ϱ \(\in ( \hbar,\hbar +1 ] \). If \(u\in C ( 0,1 ] \), \(\mathbf{T}_{0+,\theta}^{\varrho } [ u ] \in L^{1} [ 0,1 ] \), then
where \(c_{k}= \frac{u^{ ( k ) } ( 0 ) }{k!}\) and the smallest integer \(\hbar \geq \varrho (\hbar = [ \varrho ] +1)\).
Lemma 2.7
Assume that \(\theta _{2}>\theta _{1}\geq 0\) and \(u: [ \theta _{1},\theta _{2} ] \rightarrow \mathbb{R}\) is a function such that
-
(i)
u is continuous on \([ \theta _{1},\theta _{2} ] \);
-
(ii)
u is ϱ-differentiable on \(( \theta _{1},\theta _{2} ) \) for some \(\varrho \in ( 0,1 )\).
Then there exists \(\mu \in ( \theta _{1},\theta _{2} ) \) such that
Lemma 2.8
Let \(\varrho \in ( 0,1 ] \). Moreover, assume that \(u,\omega \) are ϱ-differentiable at a point \(\theta >0\). Then
-
(i)
\(T_{0+,\theta}^{\varrho } [ r_{1}u+r_{2}\omega ] =r_{1} ( T_{0+,\theta}^{\varrho } [ u ] ) +r_{2} ( T_{0+,\theta}^{ \varrho } [ \omega ] ), r_{1},r_{2}\in \mathbb{R}\).
-
(ii)
\(T_{0+,\theta}^{\varrho } [ r ] =0\) for all constant functions \(u ( \theta ) =r, r\in \mathbb{R}\).
-
(iii)
\(T_{0+,\theta}^{\varrho } [ uv ] =vT_{0+, \theta}^{\varrho } [ u ] + uT_{0+,\theta}^{\varrho } [ \omega ] \).
The predominant conformable left-sided integral operator of fractional order with \(\varrho \in ( 0,1 ],\gamma >0\), a being a positive number, and \(\theta \in ( a,\infty [ \), according to [5], is
and the conformable left-sided derivative operator of fractional order [5] is
where \(T^{\gamma,\hbar}=\) \(T^{\gamma }\circ T^{\gamma }\circ \cdots \circ T^{\gamma }\) (composition taken ħ times), \(\hbar = [ \varrho ] +1\). Besides this, \(T^{\gamma,\hbar}\) represents the right and left conformable differential operators shown in (2.2). The fractional \(\mathscr{CD}\) on the left-hand side in view of Caputo definition is defined as [5]
Lemma 2.9
([5])
Let \(\hbar \geq \varrho >\hbar -1, \varrho \notin \mathbb{N}\). Then
Lemma 2.10
([5])
For \(\alpha >0\), the general solution to Caputo-\(\mathscr{FDE}\),
is given by
with the coefficients denoted by \(c_{i} ( i=1,\dots,\hbar -1 ) \), and \(\hbar = [ \alpha ] +1\).
Lemma 2.11
([5])
When \(u ( \theta ) = ( \theta -a ) ^{ \gamma ( \nu -1 ) } \) and \(\nu >0\), we have
On the other hand, assume that \(\Lambda \in \mathbb{R}^{\hbar}\) is bounded and open, and \(u\in C^{1}(\bar{\Lambda})\). The Brouwer degree expressed as  is a framework that used extensively to describe the number of solutions for \(u(\theta )=\vartheta\) if \(\vartheta\notin u ( \partial \Lambda ) \).
is a framework that used extensively to describe the number of solutions for \(u(\theta )=\vartheta\) if \(\vartheta\notin u ( \partial \Lambda ) \).
Definition 2.12
([33])
Let \(u\in C^{1}(\bar{\Lambda})\), \(\vartheta\in \mathbb{R}^{\hbar} \) be given with \(\vartheta\notin u ( \partial \Lambda ) \) and \(\vartheta\notin u ( S_{ u} ) \). The Brouwer degree of u at ϑ in terms of Λ,  , is defined as follows:
, is defined as follows:

where  if \(u^{-1}(\vartheta)=\phi \). The Jacobian of u at θ is \(J_{u}(\theta )\). Moreover, \(S_{u} ( \bar{\Lambda} )\) is the collection including all critical points of u in Λ̄,
if \(u^{-1}(\vartheta)=\phi \). The Jacobian of u at θ is \(J_{u}(\theta )\). Moreover, \(S_{u} ( \bar{\Lambda} )\) is the collection including all critical points of u in Λ̄,
Theorem 2.13
([33])
The following are some characteristics of the Leray–Schauder degree:
(i)  iff \(0\in \Lambda \).
iff \(0\in \Lambda \).
(ii) Whenever  , \(Mu=u\) does have a solution in Λ.
, \(Mu=u\) does have a solution in Λ.
(iii) Assume that \(\mathscr{H}(u,\eta )\) maps from \(\bar{\Lambda}\times [ 0,1 ]\) to \(\mathcal{X}\) and is continuous and compact. Besides that, let \(\mathscr{H}(u,\eta )\neq u\) for every \((u,\eta )\in \partial \bar{\Lambda}\times [ 0,1 ] \). Then  .
.
Lemma 2.14
([30])
An isomorphism with a linear structure has a Leray–Schauder degree of ±1.
An algebraic projection is defined as an operator \(\mathscr{P}\) which maps from \(\mathcal{X}\) to \(\mathcal{X}\) whenever \(\mathscr{P}\) is idempotent and linear, in other words, it can be written as \(\mathscr{P}^{2}=\mathscr{P}\). Let us say that there are two algebraic projections \(\mathscr{P}\) and \(\mathscr{Q}\), where \(\mathscr{P}\) maps from \(\mathcal{X} \text{ to } \mathcal{X}\) and \(\mathscr{Q}\) maps from \(\mathcal{Y} \text{ to } \mathcal{Y.}\)
Let us consider two real Banach spaces \(\mathcal{X},\mathcal{Y}\) and suppose that \(\mathscr{L}\) mapping from  to \(\mathcal{Y}\) is a Fredholm operator having index zero, where the index of a Fredholm operator \(\mathscr{L}\) is given by
to \(\mathcal{Y}\) is a Fredholm operator having index zero, where the index of a Fredholm operator \(\mathscr{L}\) is given by

and \(\mathscr{P}\) mapping from \(\mathcal{X} \text{to} \mathcal{X}\) and \(\mathscr{Q}\) mapping from \(\mathcal{Y} \text{to} \mathcal{Y}\) are projectors such that  . then
. then  , and
, and

is invertible. We denote the inverse by \(\mathscr{K}_{\mathscr{P}}\).
If Λ is an open bounded subset of \(\mathcal{X}\) such that  , then the map \(\mathscr{N}:\mathcal{X}\rightarrow \mathcal{Y}\) will be called \(\mathscr{L}\)-compact on Λ̄ if \(\mathcal{Q}\mathscr{N} ( \bar{\Lambda} ) \) is bounded and \(\mathscr{K}_{\mathscr{P}}(\mathfrak{I}-\mathcal{Q})\mathscr{N}:\bar{\Lambda}\rightarrow \mathcal{X}\) is compact.
, then the map \(\mathscr{N}:\mathcal{X}\rightarrow \mathcal{Y}\) will be called \(\mathscr{L}\)-compact on Λ̄ if \(\mathcal{Q}\mathscr{N} ( \bar{\Lambda} ) \) is bounded and \(\mathscr{K}_{\mathscr{P}}(\mathfrak{I}-\mathcal{Q})\mathscr{N}:\bar{\Lambda}\rightarrow \mathcal{X}\) is compact.
Definition 2.15
Given two normed spaces, let us call them \(\mathcal{X}\) and \(\mathcal{Y}\). Additionally, suppose that \(\mathscr{L}\) mapping from  to \(\mathcal{Y}\) is a Fredholm operator with index zero such that:
to \(\mathcal{Y}\) is a Fredholm operator with index zero such that:
(i) \(\mathcal{Y}\) has a closed subset \(\mathrm{Im}\mathscr{L}\),
(ii)  .
.
Definition 2.16
Assume that \(\mathcal{X}\) is a normed space. An operator \(\mathscr{P}\) which maps from \(\mathcal{X}\) to \(\mathcal{X}\) is referred to as a projection if \(\mathscr{P}\circ \mathscr{P}=\mathscr{P}\). In such a case, \(I-\mathscr{P}:\mathcal{X}\rightarrow \mathcal{X}\) serves as a projection. Here  ,
,  , with I being the identity operator.
, with I being the identity operator.
The equivalence theorem of Mawhin leads to the conclusion \(\mathscr{L}u=\mathscr{N}u\) for \(u\in \bar{\Lambda}\) which is transformed to the fixed-point property \(u=\phi ( u ) \) for \(u\in \bar{\Lambda}\) here \(\phi =\mathscr{P}+(JQ+\mathscr{K}_{\mathscr{P}},_{\mathcal{Q}}N)\) is a completely continuous operator.
Theorem 2.17
([32])
Given two normed spaces, let us call them \(\mathcal{X}\) and \(\mathcal{Y}\). Let an operator \(\mathscr{L}\) mapping from  to \(\mathcal{Y}\) be a Fredholm operator with index zero and \(\mathscr{N}:\mathcal{X}\rightarrow \mathcal{Y}\) be \(\mathscr{L}\)-compact on Λ. Suppose that the conditions listed below are met:
to \(\mathcal{Y}\) be a Fredholm operator with index zero and \(\mathscr{N}:\mathcal{X}\rightarrow \mathcal{Y}\) be \(\mathscr{L}\)-compact on Λ. Suppose that the conditions listed below are met:
- (C1):
-
\(\mathscr{L}u\neq \eta \mathscr{N}u\) for every
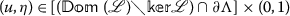 ;
; - (C2):
-
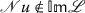 , for every
, for every 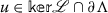 ;
; - (C3):
-
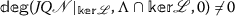 where \(\mathcal{Q}:\mathcal{Y}\rightarrow \mathcal{Y}\) is a projection such that
where \(\mathcal{Q}:\mathcal{Y}\rightarrow \mathcal{Y}\) is a projection such that 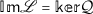 and
and 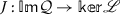 is a linear isomorphism with \(J (\Delta ) =\Delta \).
is a linear isomorphism with \(J (\Delta ) =\Delta \).
Then the equation \(\mathscr{L}u=\mathscr{N}u\) has at least one solution in  .
.
Remark 2.18
BVPs can be expressed in the form (1.1). Nonresonant problems are those in which  is invertible or
is invertible or  . Otherwise, it is referred to as a resonant problem if
. Otherwise, it is referred to as a resonant problem if  is not a simple space.
is not a simple space.
The well-known nonlinear operator called the classical p-Laplacian is frequently used in nonlinear structures. The nonlinear p-Laplacian operator is stated with \(\frac{1}{{\vartheta}}+\frac{1}{q}=1 \), thus \({\psi} _{{\vartheta}} ( {\rho} ) = \vert {\rho} \vert ^{{\vartheta}-2}{\rho}, \infty >{\vartheta}>1, {\rho} \in \mathbb{R}\mathbbm{,}\) and \({\psi} _{q}={\psi} _{{\vartheta}}^{-1}\).
Lemma 2.19
([36])
For any \(u,\omega \in \mathbb{R}\), we have
-
(i)
If \(1<{\vartheta}\leq 2\), uω is nonnegative, and \(\vert {u} \vert , \vert \omega \vert \geq l>0\), then
$$\begin{aligned} \bigl\vert \psi _{\vartheta} ( u ) -\psi _{ \vartheta} ( \omega ) \bigr\vert \leq ( \vartheta-1 ) l^{ \vartheta-2} \vert u-\omega \vert \textit{.} \end{aligned}$$(2.12) -
(ii)
If \(\vartheta>2\), \(\vert {u} \vert , \vert \omega \vert < \mathscr{L} \)then
$$\begin{aligned} \bigl\vert \psi _{\vartheta} ( u ) -\psi _{ \vartheta} ( \omega ) \bigr\vert \leq ( \vartheta-1 ) \mathscr{L}^{ \vartheta-2} \vert u-\omega \vert \textit{.} \end{aligned}$$(2.13)
Lemma 2.20
([36])
For any \(u,\omega \geq 0\), we have
-
(i)
If \(1<\vartheta<2 \) then
$$\begin{aligned} \bigl\vert \psi _{\vartheta} ( u+\omega ) \bigr\vert \leq \psi _{\vartheta} ( \omega ) +\psi _{\vartheta} ( \omega ) \textit{.} \end{aligned}$$(2.14) -
(ii)
If \(\vartheta\geq 2 \) then
$$\begin{aligned} \bigl\vert \psi _{\vartheta} ( u+\omega ) \bigr\vert \leq 2^{ \vartheta-2} \bigl( \psi _{ \vartheta} ( \omega ) + \psi _{\vartheta} ( \omega ) \bigr) \textit{.} \end{aligned}$$(2.15)
The following will be our assumptions regarding the nonlinearity of \(\mathscr{A}\). Let \(\mathscr{A}:[0,1]\times \mathbb{R}^{2}\rightarrow \mathbb{R}\) be continuous. We assume that
- (A1):
-
there exist nonnegative functions \(a,b,c\in \mathcal{Y}\) such that
$$\begin{aligned} \bigl\vert \mathscr{A}(\theta,u,\omega ) \bigr\vert \leq a(\theta )+b( \theta ) \vert u \vert ^{\vartheta-1}+c(\theta ) \vert \omega \vert ^{\vartheta-1},\quad \forall \theta \in {}[ 0,1], (u,\omega )\in \mathbb{R}^{2}. \end{aligned}$$ - (A2):
-
There is a \(\mathscr{B}>0\) such that for every \(\vert u \vert >\mathscr{B}\), one of the following occurs:
$$\begin{aligned} uf(\theta,u,0)< 0, \quad\forall \theta \in {}[ 0,1], \end{aligned}$$or
$$\begin{aligned} uf(\theta,u,0)>0, \quad\forall \theta \in {}[ 0,1]. \end{aligned}$$ - (A3):
-
For all \(\vert u \vert >\mathscr{E}\) and \(\omega \in \mathbb{R}\), there is \(\mathscr{E}>0\) such that either
$$\begin{aligned} \mathscr{A}(\theta,u,\omega )< 0,\quad \forall \theta \in {}[ 0,1], \end{aligned}$$or
$$\begin{aligned} \mathscr{A}(\theta,u,\omega )>0,\quad \forall \theta \in {}[ 0,1]. \end{aligned}$$For the sake of brevity, we use the notation \(\mathscr{A}_{u}:=\mathscr{A}(u) \equiv \mathscr{A}(\theta,u)\).
3 Solutions for the problem (1.11)–(1.12)
For the differential equation with fractional order which contains p-Laplacian (1.11), the boundary conditions (1.12) are required to solve nonlocal BVPs, and the conditions we establish in this section ensure that at least one such solution exists.
We take \(\mathcal{Y}=C [ 0,1 ] \) and
As \(u\in C[0,1]\), the pertinent norm is \(\Vert u \Vert _{\infty }=\max \{ \vert u ( \theta ) \vert : \theta \in [ 0,1 ] \} \). In addition, if \(u\in \mathcal{X}\), then the pertaining norm is
By means of the linear functional analysis theory, we can prove that \(\mathcal{X}\) is a Banach space.
The problem (1.11)–(1.12) is equivalent to the following problem:
with the condition for (3.3) being (1.12).
Define the operator  by
by
where

Let \(\mathscr{N}:\mathcal{X}\rightarrow \mathcal{Y}\) be the Nemytski operator
Then (3.3) is equivalent to the operator equation (1.1) for  .
.
The main objective of \(\mathscr{CDT}\) is to find a solution to the operator equation (3.3) with the boundary conditions (1.12) in the Banach space of operators \(\mathscr{L}\), which are either linear or nonlinear. In order to obtain the existence of solutions to (3.3) and (1.12), we require the auxiliary lemmas listed below.
Lemma 3.1
If \(\mathscr{L}\) is given by (3.4), then

and

Proof
(i) By Lemma 2.10, we have
which has solution
When the boundary value conditions of (1.12) are combined, (3.7) continues to hold.
(ii) Whenever  , suppose a function
, suppose a function  exists for which \(\mathscr{L}u=y\),
exists for which \(\mathscr{L}u=y\),
From the conditions we obtain
As a result, now we obtain (3.8). On the other hand, assume that \(y\in \mathcal{Y}\) and suppose it satisfies (3.8).
Let \(u ( \theta ) =\mathfrak{I}_{0+,\theta}^{ \alpha,\gamma } [ y ] \). Then  and
and

□
Lemma 3.2
Let \(\mathscr{L}\) be defined by (3.4). Then \(\mathscr{L}\) is a Fredholm operator of index zero, and the linear continuous projector operators \(\mathscr{P}:\mathcal{X}\rightarrow \mathcal{X}\) and \(\mathcal{Q}:\mathcal{Y}\rightarrow \mathcal{Y}\) can be defined as
and
where
Proof
(i) We have for every \(u\in \mathcal{X}\) that

Obviously,  and it is clear that \(( \mathscr{P}^{2}u ) ( \theta ) = ( \mathscr{P}x ) ( \theta ) \), \(\forall u\in \mathcal{X}\), and it follows from \(u= ( u-\mathscr{P} u ) +\mathscr{P}u\) that
and it is clear that \(( \mathscr{P}^{2}u ) ( \theta ) = ( \mathscr{P}x ) ( \theta ) \), \(\forall u\in \mathcal{X}\), and it follows from \(u= ( u-\mathscr{P} u ) +\mathscr{P}u\) that  .
.
As a result,  , implying
, implying  . Thus
. Thus

(ii) We have the following, for any \(y \in \mathcal{Y,} \)
with
By virtue of Lemma 2.11, we get (3.17).
The subsequent step is just to demonstrate  . It is indeed evident that
. It is indeed evident that  If
If  then
then
Thus we get

Let \(y\in \mathcal{Y}\), \(y= ( y-\mathcal{Q}y ) +\mathcal{Q}y\) where  .
.
Accordingly,  .
.
If  then
then
which implies that
Thus, we even have
We can get that  . Then, we now have
. Then, we now have

Hence

This indicates that the Fredholm operator \(\mathscr{L}\) has index zero,

Moreover, for the operator  , it is possible to write
, it is possible to write
and

The next step is to demonstrate that \(\mathscr{K}_{\mathscr{P}}\) is the inverse of  . It is clear again from the definitions of \(\mathscr{P},\mathscr{K}_{\mathscr{P}}\) that the generalized inverse of \(\mathscr{L}\) is \(\mathscr{K}_{\mathscr{P}}\).
. It is clear again from the definitions of \(\mathscr{P},\mathscr{K}_{\mathscr{P}}\) that the generalized inverse of \(\mathscr{L}\) is \(\mathscr{K}_{\mathscr{P}}\).
In fact, for  , we have
, we have
Furthermore, for  , we now have
, we now have

We can deduce from Lemma 2.9 that
which, together with \(u(0)=0\), yields that
Combining (3.28) with (3.30), we know that \(\mathscr{K}_{\mathscr{P}}=\mathscr{L} _{\mathscr{P}}^{-1}\). □
Lemma 3.3
Assume \(\Lambda \subset \mathcal{X}\) is a bounded open subset,  . Then \(\mathscr{N}\) is \(\mathscr{L}\)-compact on Λ̄.
. Then \(\mathscr{N}\) is \(\mathscr{L}\)-compact on Λ̄.
Proof
Consider
Considering the definition of the operator \(\mathscr{N}\) and in virtue of continuity of \(\mathscr{A}\), it can be shown that there is a constant \(\mathscr{M}>0\) such that
and
Then
and
As a result, we can conclude that \(\mathcal{Q}\mathscr{N} ( \bar{ \Lambda } ) \) is bounded:
So, we get that \(\mathscr{K}_{\mathscr{P},\mathcal{Q}} ( \bar{\Lambda } ) \) is bounded. Since \(\mathscr{K}_{\mathscr{P},\mathcal{Q}} ( \bar{\Lambda } ) =\mathscr{K}_{\mathscr{P}}(I-\mathcal{Q})\mathscr{N}( \bar{\Lambda })\subset \mathcal{X,}\) we only need to demonstrate the equicontinuity of this operator in light of the Arzelà–Ascoli theorem. For \(0\leq \theta _{1}<\theta _{2}\leq 1,u\in \bar{\Lambda }\), we have
Since \(\theta ^{\alpha \gamma }\) is uniformly continuous on \([0,1]\), we are able to get that \(\mathscr{K}_{\mathscr{P},\mathcal{Q}}(\bar{\Lambda })\subset C[0,1]\) is equicontinuous.
Analogous findings suggest that \({}^{c}\mathcal{D}_{0+,\mu }^{\alpha, \gamma } [ \mathscr{K}_{\mathscr{P}}(I-\mathcal{Q})\mathscr{N}( \bar{\Lambda }) ] \subset C[0,1]\) is equicontinuous. Now, by virtue of uniformly continuity,
is equicontinuous.
Below we mention the two cases representing how we divide the proof.
Case 1. \(1<\vartheta\leq 2\). According to Lemma 2.19 and from (3.31)–(3.36), we have
where
Case 2. \(\vartheta>2\). By (3.31)–(3.36), we have
-
(i)
Suppose that
$$\begin{aligned} \mathfrak{I}_{0+,\theta _{1}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] =0, \end{aligned}$$then \(\exists \delta _{1}>0\), for \(\theta _{2}\in [ 0,1 ] \), such that \(0<\theta _{2}-\theta _{1}<\delta _{1}\) and \(u\in \bar{\Lambda}\), and we have
$$\begin{aligned} \mathfrak{I}_{0+,\theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] >0 \end{aligned}$$and
$$\begin{aligned} \begin{aligned} &\bigl\vert {}^{c}\mathcal{D}_{0+,\mu }^{ \alpha,\gamma } [ \mathscr{K}_{\mathscr{P}, \mathcal{Q}}u ] ( \theta _{2} ) -{}^{c} \mathcal{D}_{0+,\mu }^{\alpha, \gamma } [ \mathscr{K}_{\mathscr{P},\mathcal{Q}}u ] ( \theta _{1} ) \bigr\vert \\ & \quad\leq \bigl\vert \mathscr{N}u ( \theta _{2} ) -\mathscr{N}u ( \theta _{1} ) \bigr\vert + \bigl\vert \mathcal{Q}\mathscr{N}u ( \theta _{2} ) -\mathcal{Q}\mathscr{N}u ( \theta _{1} ) \bigr\vert \\ &\quad \leq \bigl\vert \mathscr{N}u ( \theta _{2} ) -\mathscr{N}u ( \theta _{1} ) \bigr\vert , \end{aligned} \end{aligned}$$(3.43)where
$$\begin{aligned} \begin{aligned} & \bigl\vert \mathscr{N}u ( \theta _{2} ) -\mathscr{N}u ( \theta _{1} ) \bigr\vert \\ &\quad \leq \bigl\vert \mathscr{N}u ( \theta _{2} ) \bigr\vert \\ &\quad \leq \bigl\vert \psi _{q} \bigl( \mathfrak{I}_{0+, \theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] \bigr) \bigr\vert \\ & \quad\leq \bigl\vert \mathfrak{I}_{0+,\theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{u} ] \bigr\vert ^{q-1} \\ & \quad\leq \bigl\vert \mathfrak{I}_{0+,\theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{u} ] -\mathfrak{I}_{0+,\theta _{1}}^{\varrho,\gamma } [ \mathscr{A}_{u} ] \bigr\vert ^{q-1} \\ &\quad \leq \frac{1}{ ( \Gamma ( \varrho ) ) ^{q-1}} \biggl\vert \int _{0}^{\theta _{2}} \biggl( \frac{\theta _{2}^{\gamma }-\mu ^{\gamma }}{\gamma } \biggr) ^{\varrho -1}\mathscr{A}_{u} ( \mu ) \frac{\mathrm{d}\mu }{\mu ^{1-\gamma }}\\ &\qquad{}- \int _{0}^{\theta _{1}} \biggl( \frac{\theta _{1}^{\gamma }-\mu ^{\gamma }}{\gamma } \biggr) ^{\varrho -1}\mathscr{A}_{ u} ( \mu ) \frac{\mathrm{d}\mu }{\mu ^{1-\gamma }} \biggr\vert \\ & \quad\leq \frac{\mathscr{M}^{q-1}}{\gamma ^{ ( q-1 ) ( \varrho -1 ) } ( \Gamma ( \varrho ) ) ^{q-1}} \\ &\qquad{} \times \biggl\vert \int _{0}^{\theta _{1}} \bigl[ \bigl( \theta _{2}^{\gamma }-\mu ^{\gamma } \bigr) ^{ \varrho -1}- \bigl( \theta _{1}^{\gamma }-\mu ^{ \gamma } \bigr) ^{\varrho -1} \bigr] \frac{\mathrm{d}\mu }{\mu ^{1-\gamma }}\\ &\qquad{}+ \int _{\theta _{1}}^{\theta _{2}} \bigl( \theta _{2}^{\gamma }- \mu ^{\gamma } \bigr) ^{\varrho -1} \frac{\mathrm{d}\mu }{\mu ^{1-\gamma }} \biggr\vert ^{q-1} \\ & \quad\leq \frac{\mathscr{M}^{q-1}}{\gamma ^{ ( q-1 ) \varrho } ( \Gamma ( \varrho +1 ) ) ^{q-1}} \bigl\vert \theta _{2}^{\varrho \gamma }- \theta _{1}^{\varrho \gamma } \bigr\vert ^{q-1}. \end{aligned} \end{aligned}$$(3.44) -
(ii)
If
$$\begin{aligned} \mathfrak{I}_{0+,\theta _{1}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] \neq 0, \end{aligned}$$then there are two positive constants, \(\delta _{2}\) and \(l>0\), which together ensure that
$$\begin{aligned} \mathfrak{I}_{0+,\theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] \geq l>0,\quad \forall \theta _{2}\in ] \theta _{1}-\delta _{2},\theta _{1}+\delta _{2} [. \end{aligned}$$(3.45)By Lemma 2.19, we have
$$\begin{aligned} \begin{aligned} &\bigl\vert {}^{c}\mathcal{D}_{0+,\mu }^{ \alpha,\gamma } [ \mathscr{K}_{\mathscr{P}, \mathcal{Q}}u ] ( \theta _{2} ) -{}^{c} \mathcal{D}_{0+,\mu }^{\alpha, \gamma } [ \mathscr{K}_{\mathscr{P},\mathcal{Q}}u ] ( \theta _{1} )\bigr\vert \\ & \quad\leq \bigl\vert \mathscr{N}u ( \theta _{2} ) -\mathscr{N} u ( \theta _{1} ) \bigr\vert \\ &\qquad{} + \bigl\vert \mathcal{Q}\mathscr{N}u ( \theta _{2} ) -\mathcal{Q} \mathscr{N}u ( \theta _{1} ) \bigr\vert \\ & \quad\leq \bigl\vert \mathscr{N}u ( \theta _{2} ) -\mathscr{N}u ( \theta _{1} ) \bigr\vert , \end{aligned} \end{aligned}$$(3.46)where
$$\begin{aligned} \begin{aligned} &\bigl\vert \mathscr{N}u ( \theta _{2} ) - \mathscr{N}u ( \theta _{1} ) \bigr\vert \\ &\quad \leq \bigl\vert \psi _{q} \bigl( \mathfrak{I}_{0+,\theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] \bigr) -\psi _{q} \bigl( \mathfrak{I}_{0+,\theta _{1}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] \bigr) \bigr\vert \\ &\quad \leq ( q-1 ) l^{q-2} \bigl\vert \mathfrak{I}_{0+, \theta _{2}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] -\mathfrak{I}_{0+,\theta _{1}}^{\varrho, \gamma } [ \mathscr{A}_{u} ] \bigr\vert \\ &\quad \leq ( q-1 ) l^{q-2} \frac{\mathscr{M}}{\gamma ^{\varrho +1} ( \Gamma ( \varrho ) ) } \bigl\vert \theta _{2}^{\varrho \gamma }-\theta _{1}^{\varrho \gamma } \bigr\vert ,\quad \forall \theta _{2}\in ] \theta _{1}, \theta _{1}+\delta _{2} [. \end{aligned} \end{aligned}$$(3.47)Taking \(\delta =\max \{ \delta _{1},\delta _{2} \} \), the needed inequality holds for \(\theta _{2}\in ] \theta _{1}-\delta,\theta _{1}+\delta [ \).
-
(iii)
If
$$\begin{aligned} \mathfrak{I}_{0+,\theta _{1}}^{\varrho,\gamma } [ \mathscr{A}_{ u} ] < 0, \end{aligned}$$our proof is similar.
From (3.44) and (3.47), we see that \(\mathscr{K}_{\mathscr{P},\mathcal{Q}}:\bar{\Lambda }\rightarrow \mathcal{X}\) is equicontinuous. Thus, we get that \(\mathscr{K}_{\mathscr{P}}(I-\mathcal{Q})\mathscr{N}:\bar{\Lambda }\rightarrow \mathcal{X}\) is compact. □
Lemma 3.4
Suppose (A1), (A2), and (A3) hold. Then the set

is bounded.
Proof
Take \(u\in \Lambda _{1}\), then \(\mathscr{L}u=\eta \mathscr{N}u\) and 
 .
.
By (3.8), we have
consequently, according to the integral mean value theorem,
According to (\(\mathrm{A}_{3}\)), we now have
As  , we now have
, we now have
and
Thus, we have
and then
By \(\mathscr{L}u=\eta \mathscr{N}u\), we get
When the two sides of (3.52) are subjected to the operator \(\psi _{\vartheta}\), one has
From (A1) and (3.53), we get
If \(1<\vartheta<2\), from Lemma 3.4, we have
Moreover, \(\vert \psi _{\vartheta} ( {}^{c} \mathcal{D}_{0+,\theta}^{\alpha,\gamma } [ u ] ) \vert = \vert {}^{c} \mathcal{D}_{0+,\theta}^{\alpha,\gamma } [ u ] \vert ^{\vartheta-1}\) and then
So
If \(0< R_{1}= ( 1- \frac{1}{\gamma ^{\varrho }\Gamma ( \varrho +1 ) } ( \Vert b \Vert _{\infty } ( \frac{2}{\gamma ^{\alpha }\Gamma ( \alpha +1 ) } ) ^{\vartheta-1}+ \Vert c \Vert _{ \infty } ) ) \) then
and
If \(\vartheta\geq 2\) then
So
If \(0< R_{2}= ( 1- \frac{1}{\gamma ^{\varrho }\Gamma ( \varrho +1 ) } ( \Vert b \Vert _{\infty } ( \frac{2^{\vartheta-2}}{\gamma ^{\alpha }\Gamma ( \alpha +1 ) } ) ^{\vartheta-1}+ \Vert c \Vert _{ \infty } ) ) \) then
and
Using (3.57), (3.58), (3.60), and (3.61), we have
Therefore, \(\Lambda _{1}\) is bounded. □
Lemma 3.5
Suppose (A2) holds. Then the set

is bounded.
Proof
For \(u\in \Lambda _{2}\), we now have \(u(\theta )=c,c\in \mathbb{R}\) and  . Furthermore, we have
. Furthermore, we have
According to the hypothesis, a constant \(\xi \in ( 0,1 ) \) exists such that \(\mathscr{N}u ( \xi ) =0\). This can be written as
By the above-stated hypothesis, we get \(\rho\in ( 0,\xi ) \) so that \(\mathscr{A} ( \rho,c,0 ) =0\), which, in addition to (A2), essentially means \(|c|\leq \mathscr{B}\). As a result,
Hence, \(\Lambda _{2}\) is bounded. This completes the proof. □
Lemma 3.6
Assume the first part of (A2) is satisfied. Then

is bounded.
Proof
For \(u\in \Lambda _{3}^{+}\), we have \(u(\theta )=c, c\in \mathbb{R}\) and this suggests \(\psi _{\vartheta} ( {}^{c} \mathcal{D}_{0+,\theta}^{\alpha,\gamma } [ u ] ) ( 0 ) =0\) and
Whenever \(\eta =1\), we obtain \(u=c=0\).
Whenever \(\eta =0\), and following the lines of Lemma 3.3, we now have that \(\Lambda _{3}^{+}\) is bounded, i.e., \(|c|\leq \mathscr{B}\) due to first part of (A2). We now have for \(\eta \in ( 0,1 ) \) the equality
and as a result \(\mathcal{Q} ( \psi _{q} ( \mathfrak{I}_{0+,\theta}^{\varrho,\gamma } [ \mathscr{A} ( \mu,c,0 ) ] ) ) =0\). Following the lines of the proof of Lemma 3.3, we now have that \(\Lambda _{3}^{+}\) is bounded and, moreover, we can get \(|c|\leq \mathscr{B}\). Indeed, given the first part of (A2), if \(|c|>\mathscr{B}\), one will have
which contradicts (3.68). Finally, we arrived at a conclusion that \(\Lambda _{3}^{+}\) is bounded. This completes the proof. □
Remark 3.7
If second part of (A2) continues to hold, then the set

is bounded.
Theorem 3.8
Assume that \(\mathscr{A}: [ 0,1 ] \times \mathbb{R}\rightarrow \mathbb{R}\) is continuous. Assume that (A1) and (A2) hold. Then the BVP (1.11)–(1.12) has at least one solution, implying that
or
Proof
Set
Evidently, \(\Lambda _{1}\cup \Lambda _{2}\cup \Lambda _{3}\subset \Lambda \), or \(\Lambda _{1}\cup \Lambda _{2}\cup \Lambda _{3}^{-}\subset \Lambda \). It follows from Lemmas 3.1 and 3.2 that \(\mathscr{L}\) (defined by (3.4)) is a Fredholm operator of index zero and \(\mathscr{N}\) (defined by (3.6)) is \(\mathscr{L}\)-compact on Λ. By Lemmas 3.3 and 3.4, we get that the following two conditions are satisfied:
-
(i)
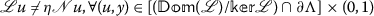 ;
; -
(ii)
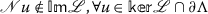 .
.
Condition (C3) of Theorem 2.17 still needs to be verified. To accomplish this, let
By Lemma 3.5, we have

Thus, by the homotopy property of degree, we have

Consequently, by using Theorem 2.17, the operator equation \(\mathscr{L} u=\mathscr{N}u\) has at least one solution in  . Thus, the BVP (1.11)–(1.12) has at least one solution in \(\mathcal{X}\). The proof is complete. □
. Thus, the BVP (1.11)–(1.12) has at least one solution in \(\mathcal{X}\). The proof is complete. □
We give one example to illustrate how our theorem can be used to solve real-world problems as we wrap up this section. Consider the \(\mathscr{FDE}\) at resonance shown below:
For the BVP (1.11)–(1.12), we take \(\vartheta=3, \gamma =2, \varrho =2/3\), and \(\alpha =3/4\).
Choose \(a(\theta )=-\frac{1}{2}\theta, b(\theta )=\frac{\theta}{2}, c( \theta )=\frac{1}{4}\theta \), and \(\mathscr{B}=\mathscr{E}=1 \). We can determine, using some basic calculation, that \(\Vert a \Vert _{\infty }= \Vert b \Vert _{ \infty }=1/2, \Vert c \Vert _{\infty }=1/4\), and
Consequently, the BVP (3.75) and (1.12) satisfies all conditions of Theorem 3.8. Hence, it has at least one solution.
4 Conclusion
By using Mawhin’s continuation theorem, we have provided some necessary conditions that, when applied to a particular kind of generalized fractional Caputo derivative and a specific type of boundary value problem with a p-Laplacian, ensure that at least one solution will exist.
Availability of data and materials
Not applicable.
References
Samko, S.G., Kilbas, A.A., Mariche, O.I.: Fractional Integrals and Derivatives. Gordon and Breach, Yverdon (1993). Translated from the 1987 Russian original.
Kilbas, A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Khalil, R., Al Horani, M., Yousef, A., Sababheh, M.: A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014)
Abdeljawad, T.: On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015)
Jarad, F., Ugurlu, E., Abdeljawad, T., Baleanu, D.: On a new class of fractional operators. Adv. Differ. Equ. 2017, 247 (2017)
Leibenson, L.S.: General problem of the movement of a compressible fluid in a porous medium. Izv. Akad. Nauk Kirg. SSR, Ser. Biol. Nauk 9, 7–10 (1983)
Lv, Z., Xu, J., O’Regan, D.: Solvability for a fractional p-Laplacian equation in a bounded domain. AIMS Math. 7(7), 13258–13270 (2022)
Kaushik, K., Kumar, A., Khan, A., Abdeljawad, T.: Existence of solutions by fixed point theorem of general delay fractional differential equation with p-Laplacian operator. AIMS Math. 8(5), 10160–10176 (2023). https://doi.org/10.3934/math.2023514
Li, Y.-L., Wang, D.-B., Zhang, J.-L.: Sign-changing solutions for a class of p-Laplacian Kirchhoff-type problem with logarithmic nonlinearity. AIMS Math. 5(3), 2100–2112 (2020). https://doi.org/10.3934/math.2020139
Jiang, W., Qiu, J., Yang, C.: The existence of solutions for fractional differential equations with p-Laplacian at resonance. Chaos 27, 032102 (2017)
Imaga, O.F., Iyase, S.A.: Existence of solution for a resonant p-Laplacian second-order m-point boundary value problem on the half-line with two dimensional kernel. Bound. Value Probl. 2020, Article ID 114 (2020). https://doi.org/10.1186/s13661-020-01415-3
Agarwal, R.P., O’Regan, D.: Infinite interval problems modeling phenomena which arise in the theory of plasma and electrical potential theory. Stud. Appl. Math. 111(3), 339–358 (2003)
Chen, T., Liu, W., Hu, Z.: A boundary value problem for fractional differential equation with p-Laplacian operator at resonance. Nonlinear Anal. 75, 3210–3217 (2012)
Dong, X., Bai, Z., Zhang, S.: Positive solutions to boundary value problems of p-Laplacian with fractional derivative. Bound. Value Probl. 2017, Article ID 5 (2017)
Hu, Z., Liu, W., Liu, J.: Existence of solutions of fractional differential equation with p-Laplacian operator at resonance. Abstr. Appl. Anal. 2014, Article ID 809637 (2014)
Bouloudene, M., Alqudah, M.M., Jarad, F., Adjabi, Y., Abdeljawad, T.: Nonlinear singular p-Laplacian four-point nonlocal boundary value problems with conformable derivative. Discrete Contin. Dyn. Syst., Ser. S 4(10), 3497–3528 (2021)
Agarwal, R.P., O’Regan, D., Stanek, S.: Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations. J. Math. Anal. Appl. 371, 57–68 (2010)
Bai, Z., Lu, H.: Positive solutions for boundary value problem of nonlinear fractional differential equation. J. Math. Anal. Appl. 311, 495–505 (2005)
Kaufmann, E.R., Mboumi, E.: Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electron. J. Qual. Theory Differ. Equ. 3, 1 (2008)
Liang, S., Zhang, J.: Positive solutions for boundary value problems of nonlinear fractional differential equation. Nonlinear Anal. 71, 5545–5550 (2009)
Zhang, S.: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electron. J. Differ. Equ. 36, 1 (2006)
Bai, Z.: Solvability for a class of fractional m-point boundary value problem at resonance. Comput. Math. Appl. 62, 1292–1302 (2011)
Kosmatov, N.: A boundary value problem of fractional order at resonance. Electron. J. Differ. Equ. 135, 1 (2010)
Tang, X., Yan, C., Liu, Q.: Existence of solutions of two-point boundary value problems for fractional p-Laplace differential equations at resonance. J. Appl. Math. Comput. 41, 119–131 (2013)
Panda, S.K., Atangana, A., Abdeljawad, T.: Existence results and numerical study on novel coronavirus 2019-nCoV/Sars-CoV-2 model using differential operators based on the generalized Mittag-Leffler kernel and fixed points. Fractals 30(08), 2240214 (2022)
Panda, S.K., Atangana, A., Nieto, J.J.: New insights on novel coronavirus 2019-nCoV/Sars-CoV-2 modelling in the aspect of fractional derivatives and fixed points. Math. Biosci. Eng. 18(6), 8683–8726 (2021)
Panda, S.K., Ravichandran, C., Hazarika, B.: Results on system of Atangana–Baleanu fractional order Willis aneurysm and nonlinear singularly perturbed boundary value problems. Chaos Solitons Fractals 142, 110390 (2021)
Panda, S.K., Abdeljawad, T., Ravichandran, C.: Novel fixed point approach to Atangana–Baleanu fractional and \(L_{p}\)-Fredholm integral equations. Alex. Eng. J. 59(4), 1959–1970 (2020)
Panda, S.K., Abdeljawad, T., Ravichandran, C.: A complex valued approach to the solutions of Riemann–Liouville integral, Atangana–Baleanu integral operator and non-linear telegraph equation via fixed point method. Chaos Solitons Fractals 130, 109439 (2020)
Gaines, R.E., Mawhin, J.L.: Coincidence Degree, and Nonlinear Differential Equations. Lecture Notes in Mathematic, vol. 568. Springer, Berlin (1977)
Mawhin, J.: Equivalence theorems for nonlinear operator equations and coincidence degree theory for some mappings in locality convex topological vector spaces. J. Differ. Equ. 12, 610–636 (1972)
Mawhin, J.: Topological degree methods in nonlinear boundary value problems. In: NSFCBMS Regional Conf. Series in Math., Am. Math. Soc., Providence (1979)
O’Regan, D., Cho, Y.J., Chen, Y.Q.: Topological Degree Theory and Applications. Chapman and Hall/CRC Press, London (2006)
Li, Y., Kuang, Y.: Periodic solutions in periodic state-dependent delay equations and population models. Proc. Am. Math. Soc. 310(5), 1345–1353 (2002)
Thompson, H.B.: Second order ordinary differential equations with fully nonlinear two point boundary conditions I, II. Pac. J. Math. 172, 255–276, 279–297 (1996)
Yan, P.: Nonresonance for one-dimensional p-Laplacian with regular restoring. J. Math. Anal. Appl. 285, 141–154 (2003)
Acknowledgements
The authors would like to thank the editor and reviewers for the valuable comments which contributed to the improvements of the article.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
Y.A., F.J., M.B and P.S.K. contributed to the design and implementation of the research, to the analysis of the results and to the writing of the manuscript.
Corresponding authors
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Adjabi, Y., Jarad, F., Bouloudene, M. et al. Revisiting generalized Caputo derivatives in the context of two-point boundary value problems with the p-Laplacian operator at resonance. Bound Value Probl 2023, 62 (2023). https://doi.org/10.1186/s13661-023-01751-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-023-01751-0
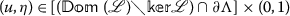 ;
;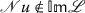 , for every
, for every 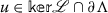 ;
;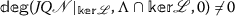 where
where 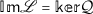 and
and 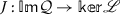 is a linear isomorphism with
is a linear isomorphism with 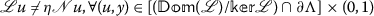 ;
;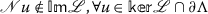 .
.