Skip to main content
Boundary Value Problems
Download PDF
  • Research Article
  • Open access
  • Published:

Removable Singularities of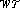-Differential Forms and Quasiregular Mappings

Boundary Value Problems volume 2007, Article number: 061602 (2006) Cite this article

Abstract

A theorem on removable singularities of-differential forms is proved and applied to quasiregular mappings.

[12345]

References

  1. Franke D, Martio O, Miklyukov V, Vuorinen M, Wisk R: Quasiregular mappings and-classes of differential forms on Riemannian manifolds. Pacific Journal of Mathematics 2002,202(1):73–92. 10.2140/pjm.2002.202.73

    Article  MATH  MathSciNet  Google Scholar 

  2. Federer H: Geometric Measure Theory, Die Grundlehren der mathematischen Wissenschaften. Volume 153. Springer, New York; 1969:xiv+676.

    Google Scholar 

  3. Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. The Clarendon Press, New York; 1993:vi+363.

    Google Scholar 

  4. Reshetnyak YuG: Space Mappings with Bounded Distortion, Translations of Mathematical Monographs. Volume 73. American Mathematical Society, Rhode Island; 1989:xvi+362.

    Google Scholar 

  5. Miklyukov V: Removable singularities of quasi-conformal mappings in space. Doklady Akademii Nauk SSSR 1969,188(3):525–527.

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Helsinki, P.O. Box 68, Helsinki, 00014, Finland

    Olli Martio

  2. Department of Mathematics, Volgograd State University, Universitetskii prospect 100, Volgograd, 400062, Russia

    Vladimir Miklyukov

  3. Department of Mathematics, University of Turku, Turku, 20014, Finland

    Matti Vuorinen

Authors
  1. Olli Martio
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vladimir Miklyukov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Matti Vuorinen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Olli Martio.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Martio, O., Miklyukov, V. & Vuorinen, M. Removable Singularities of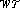-Differential Forms and Quasiregular Mappings. Bound Value Probl 2007, 061602 (2006). https://doi.org/10.1155/2007/61602

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2007/61602

Keywords